Cím: Az 1955. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1956/február, 33 - 40. oldal  PDF  |  MathML 
Témakör(ök): Ábrázoló geometria

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Bizonyítandó, hogy ha a trapéz alapján nyugvó szögek nem egyenlők, akkor a kisebbiknek csúcsából kiinduló átló a hosszabb.

 

I. megoldás. Segédtételként előre bocsátjuk a következő megállapítást: Ha két derékszögű háromszögben az egyik befogó ugyanakkora, és a két háromszög nem egybevágó, akkor ugyanabban a háromszögben található a másik befogóknak és az átfogóknak nagyobbika az egyenlő befogókkal szemközti szögeknek pedig kisebbike. Ennek belátására fektessük egymásra a két háromszöget úgy, hogy derékszögeik és egyenlő befogóik fedjék egymást (1. ábra).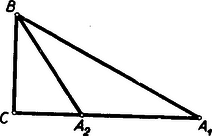
 
 
1. ábra
 

Az egyiknek CA1 befogója túlnyúlik ebben a helyzetben a másiknak CA2 befogóján, hiszen a háromszögek nem egybevágók. A keletkező A1A2B▵ tompaszögű, s ezért BA1>BA2. Ugyanennek a háromszögnek külső szögére vonatkozólag viszont 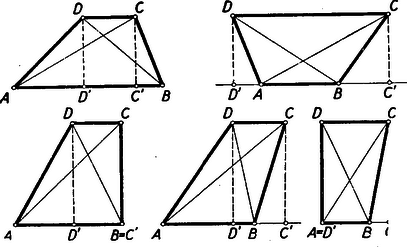BA1C∢<BA2C∢ adódik.
 
 
2. ábra
 

Tekintsük most már az ABCD trapéz AB alapján nyugvó szögeket (2. ábra), és legyen
DAB∢<CBA∢.(1)
A C és D csúcsot az AB egyenesre vetítve a C' és D' pontokhoz jutunk. Bizonyítanunk kell az
AC>BD(2)
egyenlőtlenséget. Elegendő ehhez az
AC'>BD'(3)
egyenlőtlenséget bizonyítanunk. Ha ugyanis BD'≠0, akkor segédtételünket az ACC' és BDD' háromszögekre alkalmazva (3)-ból (2) adódik. Ha viszont B és D' azonos, akkor BD=CC', és így (2) abból adódik, hogy az ACC' derékszögű háromszög átfogója a befogónál hosszabb.
(3) bizonyításánál a DAB és CBA szög minőségének megfelelően három esetet különböztetünk meg.
1. Ha mindkettő hegyesszög, akkor segédtételünket az ADD' és BCC' háromszögekre alkalmazva (1) alapján AD'>BC' adódik, és az ezeket AB-re kiegészítő szakaszokra (3) érvényes. 2. Ha mind a két szög tompaszög, akkor ismét az ADD' és BCC' háromszögekre alkalmazzuk segédtételünket. Most azonban DAD'∢>CBC'∢, mert ezek az (1)-ben szereplő szögeknek kiegészítő szögei. A segédtétel alapján tehát AD'<BC', és ezeket AB-vel megnövelve (3) adódik.
3. Ha DAB∢≤90∘ és CBA∢≥90∘, akkor az AB egyenesen az AB→ irányban haladva D' nem lehet A előtt, és C' nem lehet B előtt. Az AC' szakasz tartalmazza tehát a BD' szakaszt. Ez utóbbi nem lehet AC'-vel azonos sem, mert (1) miatt nem lehet mind a két szereplő szög derékszög. A részként tartalmazott szakasz hosszára tehát teljesül a (3) egyenlőtlenség.
 

II. megoldás. Növeljük meg az ABCD trapéz AB alapján nyugvó kisebbik, DAB∢-ét akkorára, amekkora a CAB∢. Így az egyenlő szárú ABCE trapézhez jutunk (3. ábra), melynek átlói a szimmetria miatt az AB szakasz felezőmerőlegesén metszik egymást.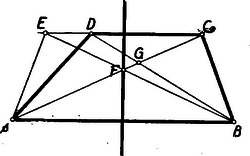
 
 
3. ábra
 

Ezt az F metszéspontot C-vel összekötő FC szakasz a felezőmerőlegesnek azon az oldalán van, amelyiken a B pont. Ugyanezen az oldalon van tehát az eredeti trapéz átlóinak G metszéspontja is, hiszen a D pont az EC szakasz belsejében van, és a BCE▵-ből az adódik, hogy BD metszi az FC szakaszt. Minthogy az AB szakasz felezőmerőlegese által meghatározott félsíkok közül a B pontot tartalmazónak pontjai közelebb vannak B-hez, mint A-hoz, ez áll a G pontra, azaz
GA>GB.
Az ABG▵ és CDG▵ hasonló, mert szögeik páronként csúcsszögek, ill. váltószögek. A bizonyított egyenlőtlenség következményeként tehát
GC>GD.
Egyenlőtlenségeink összegezésével a bizonyítandó AC>BD egyenlőtlenséget kapjuk.
 

III. megoldás. Az ABCD trapéz AB alapján nyugvó kisebbik szög növelésével egyenlő szárú ABCE trapézhez jutunk (4. ábra). E trapéz szimmetria‐tengelye az EC szakasz felezőmerőlegese. Minthogy B ennek a felezőmerőlegesnek azon az oldalán van, amelyiken a felezett CE szakasz C végpontja, azért BC<BE. A szimmetria folytán AC=BE. A BCD és BDE háromszögek D-nél fekvő szögei egymást 180∘-ra egészítik ki, ezért e szögeknek valamelyike vagy hegyesszög vagy tompaszög. Minthogy a tompaszöggel szemben a háromszögnek legnagyobb oldala helyezkedik el, a két háromszögnek valamelyikéből az következik, hogy BD kisebb a BE és BC szakaszok valamelyikénél, tehát kisebb e szakaszok nagyobbikánál, az AC-vel egyenlő BE szakasznál.
 

IV. megoldás. Az ABCD trapézt, az AB átlón nyugvó kisebbik szöget növelve, szimmetrikus ABCE trapézzé egészítjük ki (4. ábra).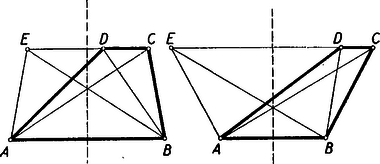
 
 
4. ábra
 

A háromszög külső szögére vonatkozó egyenlőtlenség szerint
EDB∢>DCB∢,
a szimmetria miatt pedig
DCB∢=AED∢.
Így tehát a BDE▵-ben D-nél nagyobb szög helyezkedik el, mint E-nél, mert a BED▵ része az AED∢-nek, amelyről beláttuk, hogy EDB∢-nél kisebb. Minthogy egy háromszögben nagyobb szöggel szemben nagyobb oldal van, így BE>BD. Ezzel a feladat állítását bizonyítottuk, hiszen a szimmetria miatt AC=BE1.
 

Második feladat. Hány olyan 3-mal osztható ötjegyű szám van amelyben előfordul a 6-os számjegy?
 

I. megoldás. A 6-ost tartalmazó, 3-mal osztható, ötjegyű számokat csoportosítsuk aszerint, hogy utolsó 6-os jegyük az egyesektől számítva hányadik jegy.
Az első csoportba azok a számok tartoznak, amelyeknek utolsó jegye 6-os, ilyen számhoz úgy jutunk, hogy a három közbenső jegyet tetszőlegesen választjuk meg, s ezután az első jegyet úgy választjuk meg az ide írható 9 jegy közül (mert 0 nem lehet első jegy), hogy a jegyek összege 3-mal osztható legyen. A közbenső jegyek mindegyikének megválasztásánál 10 lehetőség van, az első jegy megválasztásánál viszont csak 3 a lehetőségek száma, mert a már megválasztott jegyek összegétől függően vagy az 1, 4, 7, vagy a 2, 5, 8, vagy pedig a 3, 6, 9 jegyek közül választhatunk, hiszen valamennyi jegy összege kell, hogy 3-mal osztható legyen. Az első csoportba tartozó számok száma ezek szerint 3⋅103=3000.
A második, harmadik és negyedik csoportba tartozó számoknál a tízes, százas, ill. ezres jegy 6-os, és ezt követően 6-os jegy már nem szerepel. Ilyen számot keresve az ezt a 6-os jegyet követő jegyeket szabadon választhatjuk 9 jegy közül, hiszen 6-ost nem választhatunk, a megelőző jegyeket az elsőnek kivételével tetszőlegesen választhatjuk meg a 10 jegy közül. Az első jegy megválasztásánál ugyanaz a megkötés érvényesül, mint az első csoport esetében, e jegy megválasztásánál tehát mindig 3 lehetőség van. Ezekbe a csoportokba tehát rendre 3⋅102⋅9=2700, 3⋅10⋅92=2430, 3⋅93=2187 szám tartozik.
Az ötödik csoport számainak tízezres jegye 6-os, a többi nem hatos. Egy ilyen szám megválasztásánál a három közbenső jegyet szabadon választhatjuk a 9 megengedett jegy közül, hiszen 6-ost nem választhatunk. Az utolsó jegyet e 9 jegy közül úgy választjuk meg, hogy a szám jegyeinek összege 3-mal osztható legyen. Az utolsó jegy megválasztásánál a többi jegy összegétől függően az 1, 4, 7 vagy a 2, 5, 8, vagy pedig a 0, 3, 9 jegyek közül válogathatunk, tehát minden esetben 3 lehetőségünk van. Az ötödik csoportba ezek szerint 3⋅93=2187 szám tartozik.
Valamennyi csoportban együtt 3000+2700+2430+2187+2187=12504 szám van.
 

II. megoldás. Először az ötjegyű, 6-ost tartalmazó számok számát határozzuk meg, tekintet nélkül arra, hogy vajon 3-mal oszthatók-e vagy sem. Ezután majd bizonyítjuk, hogy mind e számoknak éppen a harmada osztható 3-mal.
1. Jelöljük az n jegyű, 6-ost tartalmazó számok számát f(n)-nel. Vizsgáljuk az n+1 jegyű, 6-ost tartalmazó számokat, s ezeket soroljuk két csoportba aszerint, hogy utolsó jegyük 6-os vagy nem 6-os.
Az első csoporthoz tartozó számokat úgy kapjuk meg, hogy egy tetszőleges, n jegyű számhoz még egy 6-os jegyet fűzünk hozzá. Az első csoporthoz tartozó számok száma tehát a 10n-1-től 10n-ig terjedő, n jegyű számok számával egyenlő, azaz 10n-10n-1.
A második csoportba tartozó számot úgy kapunk, hogy egy n jegyű, 6-ost tartalmazó számhoz hozzáfűzünk egy 6-ostól különböző jegyet. Mivel ekkor 9 lehetőség van, a második csoportba tartozó számok száma 9f(n).
A két csoporthoz tartozó számok együttes száma ezek szerint
f(n+1)=10n-10n-1+9f(n).
Minthogy egyetlen egyjegyű, 6-ost tartalmazó szám van, f(1)=1. Ebből kiindulva a levezetett összefüggés felhasználásával sorra a következő értékekhez jutunk: f(2)=18, f(3)=252, f(4)=3168, f(5)=37512.
2. Nyilvánvaló, hogy ha egy számtani sorozat elemeinek száma 3-mal osztható, és a különbség 3-mal osztva maradékul 1-et ad, akkor a sorozat elemeinek éppen a harmada osztható 3-mal. Több ilyen sorozat elemeinek együttesére is igaz ez a megállapítás, feltéve, hogy a sorozatoknak nincs közös elemük. Az ötjegyű, 6-ost tartalmazó számokról fentebb kimondott állításunkat bizonyítjuk tehát, ha e számokat közös elem nélküli, 3-mal osztható elemszámú, 3-mal osztva maradékul 1-et adó különbségű számtani sorozatokba soroljuk. Ezt a következőképpen tesszük:
A 6-osra végződő számok egy 10 006-tal kezdődő 99 996-ra végződő, 9000 elemű, 10 különbségű számtani sorozatot alkotnak. A más jegyre végződő számokat olyan csoportokba gyűjtjük, amelyekben csak az utolsó jegy az eltérő. Minden egyes ilyen csoportban a 0, 1, 2, 3, 4, 5 jegyekre végződő számok egy 6 eleme, 1 különbségű, és a 7, 8, 9 jegyekre végződők egy 3 elemű, 1 különbségű számtani sorozatot alkotnak.
Mivel mind e sorozatok megfelelnek követelményeinknek, igazoltuk, hogy az ötjegyű, 6-ost tartalmazó számoknak harmada, azaz 37512:3=12504 osztható 3-mal.
 

III. megoldás. Ismét először valamennyi ötjegyű, 6-ost tartalmazó számnak számát határozzuk meg, majd bizonyítjuk, hogy ezeknek harmada osztható 3-mal.
 

1. Összesen 90 000 ötjegyű szám van. Az ötjegyű, 6-ost nem tartalmazó számok számát határozzuk meg. Ilyen számot úgy kapunk, hogy első jegynek a 0 és 6 kizárásával maradó 8 jegy közül választunk egyet, a többi jegy megválasztásánál pedig csak a 6-ost zárjuk ki, azaz mind a négy esetben 9 lehetőség között választunk. Az ötjegyű, 6-ost nem tartalmazó számok száma tehát 8⋅94=52488. Az ötjegyű, 6-ost tartalmazó számok száma tehát 90000-52488=37512. Ez 3-mal osztható szám.
 

2. Írjuk fel növekvő rendben az ötjegyű számokat. Tagoljuk ezt a sorozatot tízes szakaszokba, egy‐egy szakaszba foglalva azokat a számokat, amelyek csak az utolsó jegyben különböznek egymástól. Jelöljük meg mindegyik szakaszban a 6-ost tartalmazó számokat. Vannak szakaszok, amelyekben minden számot megjelölünk, ti. azokban a szakaszokban, amelyeknek nem változó, első jegyei között 6-os is szerepel. A többi szakaszban csak egy‐egy számot, a 6-osra végződőt jelöljük meg.
••••••••••∘∘∘∘∘∘•∘∘∘}{••••••••••∘∘∘∘∘∘•∘∘∘5. ábra



Vizsgáljuk meg, mekkora lehet a különbség két‐két, egymáshoz legközelebbi megjelölt szám között.1 Ha e két szám ugyanahhoz a szakaszhoz tartozik, a szakasz csupa megjelölt számból áll, és a különbség 1. Ugyancsak 1 a különbség, ha a két szám két szomszédos, csupa megjelölt számból álló szakaszhoz tartozik. Ha a tekintett két szám közül a kisebbik egy csupa megjelölt számból álló szakaszhoz, a nagyobbik meg nem ilyenhez tartozik, akkor a különbség 7. Ha a nagyobbik tartozik csupa megjelölt számból álló, s a kisebbik meg nem ilyen szakaszhoz, akkor különbségük 4. Ha végül mindkét szám olyan szakaszhoz tartozik, amelynek nincs minden száma megjelölve, akkor 10 a különbségük. A vizsgált különbség lehetséges értékei 1, 4, 7, 10.
 

Minthogy e számok mindegyike 3-mal osztva 1-et ad maradékul, megállapíthatjuk, hogy a megjelölt számok nagyság szerinti egymásutánjában minden harmadik osztható 3-mal, hiszen minden 3-mal osztható számra olyan következik ebben az egymásutánban, amelyik 3-mal osztva 1-et ad maradékul, erre olyan amelyik 2-t ad maradékul, s erre megint egy 3-mal osztható következik. Minthogy a megjelölt számok száma osztható 3-mal, ezeknek harmada, azaz 37512:3=12504 osztható 3-mal.
 

IV. megoldás. A 90 000 ötjegyű szám között minden harmadik tehát összesen 30 000 osztható 3-mal. Határozzuk meg, hogy ezek között hány 6-ost nem tartalmazó van.
 

Egy ilyen szám első jegyét 8-féleképpen választhatjuk meg, mert 0 és 6 nem választható. A második, harmadik és negyedik jegy megválasztásánál 9 lehetőség van, hiszen csak a 6-os választását kell kizárnunk. Az utolsó jegyet úgy kell megválasztanunk, hogy a jegyek összege 3-mal osztható legyen. A már megválasztott jegyek összegétől függően tehát vagy az 1, 4, 7 vagy a 3, 5, 8, vagy pedig a 0, 3, 9 jegyek között, vagyis mindig 3 lehetőségből választhatunk.
Az ötjegyű, 6-ost nem tartalmazó, 3-mal osztható számok száma ezek szerint 8⋅93⋅3=17496, az ötjegyű, 6-ost tartalmazó, 3-mal oszthatóké pedig 30000-17496=12504.
 

Harmadik feladat. Rácspontoknak nevezzük a síknak azokat pontjait amelyiknek mindkét koordinátája egész szám. Bizonyítandó, hogy ha egy háromszög csúcsai rácspontok, a határán több rácspont nincs, és belsejében egyetlen rácspont van, akkor ez a rácspont a háromszög súlypontja.
 

I. megoldás. Először belátjuk, hogy ha egy rácspontot egy másik rácspontra, vagy pedig két rácspont összekötő szakaszának felezőpontjára tükrözünk, akkor a tükörkép rácspont. Tudjuk ugyanis, hogy ha az A pontot B-re tükrözve a C ponthoz jutunk, akkor A és C megfelelő koordinátáinak összegei a B pont megfelelő koordinátáinak kétszeresével egyenlők. Két rácspont összekötő szakaszának felezőpontjáról tudjuk tehát, hogy koordinátáinak kétszeresei egész számok. Még inkább igaz ez egy rácspontra, hiszen egész számok kétszeresei is egész számok. Ha most egy rácspontot ilyen pontra tükrözünk, akkor megállapításunk értelmében a tükrözött rácspont és a tükrözéssel nyert pont megfelelő koordinátáinak összegei egész számok. A tükrözéssel kapott pont tehát rácspont, mert koordinátái egész számok különbségei.
Tekintsük most már a feladatban szerepeltetett ABC háromszöget, s az ennek belsejében levő S rácspontot. Tükrözzük mind e pontokat az ABC▵ oldalainak felezőpontjaira (6. ábra).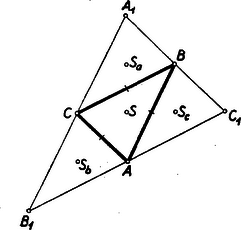
 
 
6. ábra
 

Valamennyi kapott pont rácspont. A kapott csatlakozó A1BC, AB1C, ABC1 háromszögek belsejében van rendre az S-ből tükrözéssel nyert Sa, Sb, Sc rácspont. E háromszögek belsejében több rácspont nincs, mert ha pl. az A1BC▵ még egy rácspontot tartalmazna, akkor ezt BC felezőpontjára tükrözve az ABC▵-ön belüli második rácsponthoz jutnánk.
Tükrözzük most az A1 rácspontot Sa-ra. Az így kapott rácspont az A1B1C1 belsejében van, mert az A1 pontból való kétszeres kinagyítás az A1BC▵-et az A1B1C1▵-be, az Sa pontot pedig a szóban forgó rácspontba viszi. Ez a rácspont tehát az S, Sa, Sb, Sc rácspontok valamelyikével azonos, hiszen a fentiek szerint az A1B1C1▵ belsejében nincs más rácspont. Minthogy Sa-ra tükröztünk, Sa maga nem lehet ez a tükörkép. Bizonyítjuk, hogy Sb és Sc sem lehet. Elegendő ezt pl. Sc-re bizonyítanunk. Az AS szakasz tükörképe BC és AB felezőpontjára az A1Sa és BSc szakasz. E szakaszok tehát AS-sel, s így egymással is párhuzamosak és egyenlők. Ezért A1SaSbB paralelogramma, és Sc valóban nem lehet A1-nek Sa-ra vonatkozó tükörképe.
 

Beláttuk így, hogy A1-nek Sa-ra vonatkozó tükörképe csak az S rácspont lehet. Ebből az következik, hogy A1, Sa, S egy egyenesen van. Ez az egyenes áthalad SSa és BC közös felezőpontján, tartalmazza tehát A1-nek e felezőpontra vonatkozó tükörképét, az A pontot is. Eszerint S rajt van az ABC▵ A-ból induló súlyvonalán. Az A, B, C pontok szerepének azonossága miatt rajta van akkor a másik két súlyvonalon is, ezért S az ABC▵ súlypontja.
 

II. megoldás. Felhasználjuk az első megoldás első bekezdésében kimondottakat. Eszerint egy rácspontból való kétszeres kinagyítás minden rácspontot rácspontba visz.
Legyen ismét S a szerepeltetett ABC▵ belsejében levő rácspont. Az S pontnak e háromszög középvonalai által alkotott A'B'C'▵ belsejében kell lennie (7. ábra), mert ha pl. az AB'C'▵ tartalmazná az S pontot, akkor az A pontból való kétszeres kinagyítás S-et az ABC▵ által tartalmazott újabb rácspontba vinné.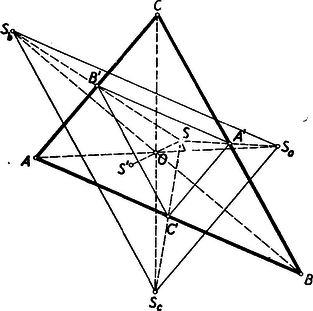
 
 
7. ábra
 

Az S pontot az A', B', C' pontokra tükrözve az Sa, Sb, Sc rácspontokat kapjuk. Az ASa, BSb, CSc szakaszoknak közön O felezőpontjuk van. Ezt pl. az ASa és BSb szakaszokra abból következtetjük, hogy ABSa Sb paralelogramma, hiszen AB és SaSb párhuzamosak és egyenlők, mert mindkettő az A'B' szakasznak (C-ből, ill. S-ből való) kétszeres kinagyításával keletkezik.
Az S pontnak O-ra vonatkozó tükörképe egy S' rácspont. Minthogy S az A'B'C'▵-ben, tehát még inkább az SaSbSc▵ belsejében helyezkedik el, azért S' e háromszög O-ra vonatkozó tükörképében, az ABC▵-ben van. Minthogy azonban ebben a háromszögben csak egyetlen rácspont van, kell, hogy S egybeessék S'-vel, tehát O-val is.
Ezek szerint az AS, BS, CS egyenesek azonosak az SSa, SSb, SSc egyenesekkel, tehát áthaladnak az A', B', C' pontokon. Ezek az egyenesek tehát az ABC súlyvonalai, és S a súlypontja.
 

III. megoldás. Háromszögünket egyik oldalának felezőpontjára tükrözve paralelogrammához jutunk. E paralelogramma belsejében tartalmazza a háromszögünk belsejében levő rácspontot és annak tükörképét, több rácspontot azonban nem. Ezt már az első megoldás bevezető részében is beláttuk. Elég ezért a következő állítást bizonyítanunk.
Ha egy paralelogramma csúcsai rácspontok, a határán több rácspont nincs, és belsejében két rácspont van, akkor ezek a paralelogrammának egy átlóján vannak, s azt harmadolják.
Először azt látjuk be, hogy egy paralelogramma belsejében levő ponthoz mindig található a paralelogrammának olyan csúcsa, hogy az e csúcsból való kétszeres kinagyítás azt a pontot a paralelogrammához tartozó pontba viszi. Ez nyomban következik abból, hogy a paralelogrammát két középvonala négy paralelogrammára bontja, és ezeknek mindegyike egy‐egy csúcsból kétszeresre nagyítva a teljes paralelogrammába megy át. Tekintsük most már az állításunkban szerepeltetett paralelogrammát, és az ennek belsejében elhelyezkedő S és T rácspontokat (8. ábra).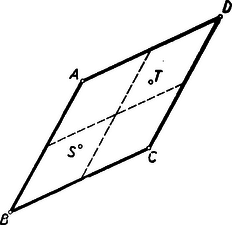
 
 
8. ábra
 

Nem szerepelhet ezek között a paralelogramma középpontja, mert akkor a másiknak erre vonatkozó tükörképe a paralelogramma belsejében elhelyezkedő harmadik rácspontot adna.
Az előre bocsátottak szerint a paralelogramma egyik B csúcsának S-re vonatkozó tükörképe a paralelogrammához tartozik. Ez a tükörkép nem lehet a paralelogrammának csúcsa, mert S nincs a paralelogramma határán és nem azonos a paralelogramma centrumával. Kell tehát, hogy e tükörkép a T pont legyen.
Ugyanígy adódik, hogy egy D csúcsnak T-re vonatkozó tükörképe S-sel azonos. Ezzel beláttuk, hogy S és T harmadolják a BD szakaszt. BD a paralelogrammának csak átlója lehet, hiszen S és T nem lehet a paralelogramma határán. Ezzel állításunkat bizonyítottuk.
 

IV. megoldás. Ismét támaszkodunk az első megoldás első bekezdésében kimondottakra.
A feladatban szereplő ABC▵-et súlyvonalai hat háromszögre bontják (9. ábra).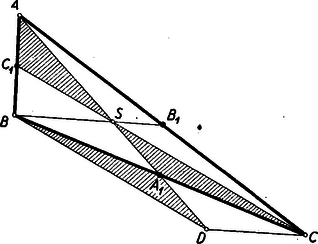
 
 
9. ábra
 

Az ABC▵ belsejében levő egyetlen rácspontot e hat háromszögnek legalább egyike, pl. az AC1S▵ belsejében vagy határán tartalmazza, nem lehet azonban e rácspont az AC1 szakaszon. Az A pontból való kétszeres kinagyítás ezt a rácspontot olyan újabb rácspontba viszi, amelyik az AC1S▵ kinagyításával kapott ABD▵-ben vagy annak határán van, de nincs az AB szakaszon. Minthogy az ABC▵ nem tartalmazhat belsejében második rácspontot, az újabb rácspontnak az A1BD▵-ben vagy annak határán kell lennie, de B-vel azonos nem lehet. Ha most ezt a háromszöget az általa tartalmazott rácsponttal együtt az A1 pontra tükrözzük, azt kapjuk, hogy az A1CS▵-ben vagy annak határán van egy C-től különböző rácspont. Ez a rácspont csak az ABC▵-ben levő egyetlen, AC1S▵ által is tartalmazott rácspont lehet. Ez az egyetlen rácspont azonos tehát háromszögünk S súlypontjával, hiszen az AC1S és A1CS háromszögeknek nincs más közös pontja.
 

Megjegyzés. A harmadik feladat állításának térbeli megfelelője nem igaz: van olyan tetraéder, melynek csúcsai rácspontok, határán nincs több rácspont, és belsejében egyetlen, a tetraéder súlypontjától különböző rácspont van. Így pl. az A(0, 0, 0), B(1, 0, 0), C(0, 1, 0), D(2, 2, 5) csúcsok által adott tetraéder csak az R(1, 1, 2) rácspontot tartalmazza belsejében, és ez a tetraédernek nem súlypontja.
1Ez a megoldás szerepel a Mathematikai versenytételek, I. rész (Középiskolai szakköri Füzetek, Tankönyvkiadó, 1955) 70. oldalán.

1Az 5. ábra szemlélteti a számba vett lehetőségeket. Ezen az ábrán a fekete körök megjelölt számokat, a fehér körök meg nem jelölt számukat jelképeznek.