Cím: A "Fogas kérdések" meoldása a XVIII. kötet 1. számából
Füzet: 1959/október, 65 - 68. oldal  PDF  |  MathML 
Témakör(ök): Ábrázoló geometria

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I.

1,23,456,790     Írjuk fel azt a legkisebb természetes számot, amely a keretben nincs megemlítve.
 

Megoldás: A keret nemcsak a megadott négy számot tartalmazza, hanem a feladat szövegét is. Ezért nem lehet teljesíteni a felszólítást, az ugyanis ellentmondást tartalmaz. Ugyanis a főmondat rámutat arra ‐ más szóval: említi azt, amit fel kíván íratni; és éppen ennél a megemlítésnél fogva nincs mg a kívánt valaminak a (jelzői) mellékmondatban közölt tulajdonsága, hogy ti. nincs megemlítve a keretben, élesebben mondatban.
Hogy a felírni kívánt valami egy szám, ez lényegtelen; az ellentmondás a következőkben van benne: ,,Írjuk fel azt ..., ami ebben a mondatban nincs megemlítve".
 

Katona Mária (Budapest, Szilágyi E. lg. I. o. t.) dolgozata, kiegészítéssel
 

Megjegyzés: Egy dolgozat szerint: 8222;a megfelelő szám 8, mert a 7 és a 9 között nincs szám. A feladat kissé cseles (kétértelmű), a 2-re is lehetett gondolni,..., de ez előfordul a 23-ban8221;. További 18 rövidebb dolgozat szintén a 8-at, 11 dolgozat a 2-t tartja megoldásnak. ‐ Eszerint legalább 19-en nem tudtak különbséget tenni szám és számjegy között; olyasmi ez, mintha összekevernők az írott szót a betűvel, a kimondott szót a hanggal. Másrészt 11-en nem érezték meg, hogy a ,,fogas" kérdésekben valóban van valami ,,cseles", vagy legalábbis szokatlan, és egészen gyermekesen ,,lépre mentek".
 

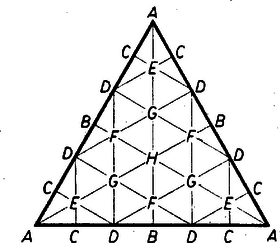
II. Hány háromszög látható a mellékelt ábrán?
 
 

Megoldás: A szimmetriákat felhasználva a háromszögek megszámlálását egyszerűsíthetjük, a szimmetrikus csomópontok az ábrán azonos betűvel vannak jelölve.* A rendszerezésben a háromszögek alakját is figyelembe vesszük. 8212;- A szerepló 6 irány közül bármely 2 között a szög 30∘,60∘ vagy 90∘, így a háromszögekben fellépő legkisebb szög 30∘, és a legnagyobb szög 180∘-2⋅30∘=120∘. Eszerint 3-féle háromszög-alak fordul elő, szögeik : 30∘,30∘,120∘(T1); 30∘,60∘,90∘(T2); 60∘,60∘,60∘(T3). Célszerű még a háromszögek területét is megadni, egységnek az előforduló legkisebb T2-alakú háromszög területét véve.
Az T1 alak legkisebb előfordulása a 2 egységnyi ADE, ill. DDF típus, ilyen 6, ill. 3 van; ennek lineárisan 2-, ill. 3-szoros nagyítása a 8, ill. 18 egységnyi ADG, ill. AAH típus, 6, ill. 3 van belőle, tehát T1 alakú háromszög 6+3+6+3=18 van.
A T3 alak 4-féle nagyságban fordul elő, legkisebb a 2 egységnyi DEG,DFG és FGH típus 68212;6 példányban, ennek 2-, 3-, ill. 33-szoros nagyítása a 8, 18, 54 egységnyi DFG,DDD,AAA típus, 6, 2, ill. 1 példányban, ezek szerint 18+6+2+1=27 szabályos háromszöget látunk.
Végül a T2 alak 68212;6 AEC,DEC,DFB típusú 1 egységnyi háromszöggel, továbbá ennek 6-féle nagyításával szerepel : 2, 3, ill. 4-szeres nagyításai a 4, 9, 16 egységnyi AGD és DGD, ill. AHB és DDC, ill. AFD típusú háromszögek, és 3,23,33-szoros nagyításai a 3,12,27 egységnyi ADC,ADD,AAB típusú háromszögek, valamennyi 6 példányban, ilyen háromszög tehát 11⋅6=66 van az ábrán.
Ezek szerint a háromszögek összes száma 18+27+66=111.
 

S. Nagy Erzsébet (Makó, József A. g. IV. o. t.)
 

Megjegyzések: l. Más rendszerezés: minden egyes A típusú csomópontban 6 T1 alakú háromszögnek 30∘-os szöge van, 10, ill. 6 T2 alakúnak 30∘-, ill. 60∘-os szöge van, végül 1 T3 alakúnak 60∘-os szöge, tehát egy ilyen csúcs összesen 23 háromszöghöz tartozik hozzá. Hasonlóan minden B,C,...,G típusú csomópont 6,4,18,8,11,14 háromszögnek, a H csomópont pedig 15 háromszögnek csúcsa. E számokat a megfelelő típusú csomópontok 3,3,6,63,3,3,1-es létszámával szorozva 69+18+24+108+24+33+42+15=333 háromszögcsúcsot kapunk, és így a háromszögek száma 111.
2. A legtöbbször előforduló téves eredmény 105, ezekből többnyire a 16 egységnyi AFD típusú háromszögek száma hiányzik.
 

III. Egy 3 cm élű sajtkockát 1 cm élű kockákra akarunk szétvágni. Legalább hány vágás szükséges ehhez, ha a darabokat már a második vágás előtt is átrendezhetjük, de vágás alatt nem nyúlhatunk hozzájuk? ‐ Hány vágással érünk célhoz, ha egy 6×9×20 cm-es és egy 7×10×30 cm-es tégla alakú sajttömböt akarunk ugyancsak köbcentiméteres darabokra vágni? (A kés ‐ vagy kifeszített húr ‐ hossza ,,elég nagy".)
 

Megoldás: Egy egyenes rúd v vágással legfeljebb 2v darabra vágható szét, ha minden vágás előtt valamennyi vágni kívánt darabot párhuzamos nyalábba fogva tesszük a kés alá. Fordítva : ha egy rudat a fenti módon n részre akarunk vágni és 2v-1<n<2v, akkor ehhez legalább v vágásra van szükség. Ha a részeket egyenlőknek kívánjuk, akkor akár n=2k, akár n=2k+1 esetén az első vágásban pl. úgy vághatunk, hogy egyik rész k/n-ed része legyen a rúdnak, azonban semmi esetre sem hagyhatunk 2v-1/n-résznél hosszabb darabot, különben ennek a szét vágása is legalább v vágást igényel.
Így a sajtkocka mindhárom kiterjedésének irányában 2 vágásra van szükség, összesen 6-ra, mert 21<3≤22-ből v=2. Ezt abból is beláthatjuk, hogy a 33=27 db kis sajtkocka közül 1 teljesen ,,héjatlan"; lesz, és ennek mind a 6 lapját külön vágással keli kialakítanunk.
A téglatestek él-méretei alapján mindkét esetben V=v1+v2+v3=3+4+5=12 (alkalmasan elhelyezett) vágásra van szükség. Ugyanis a háromirányú vágások közben hiábavaló volna az eljárást avval siettetni próbálni, hogy némely, valamelyik irányban már csak 1 cm kiterjedésű, és emiatt a vágásból átmenetileg kimaradó darabot elforgatva tegyünk a kés alá, hiszen az el nem forgatott darabok miatt a megállapított számú vágást úgyis el kell végeznünk.
 

Pósch Margit (Budapest, Veres Pálné lg. I I I . o. t.)
 

Megjegyzés: A dolgozatok nem vették figyelembe a feladat fogalmazásának azt a ,,fogas-cseles"; finomságát, hogy egy 6×9×20 és egy 7×10×30 cm-es tömböt akarunk szétvágni. Ehhez összesen 12 vágás elegendő, a kisebb tömb a nagyobb mellett mindig ,,elcsúszik".
 

IV. Péter, miután egy számnak kikereste a (tízes alapú) logaritmusát, így kiáltott fel: ezt úgy is megkaphattam volna, ha a számban a tizedes vesszőt egy hellyel elírom! Mi lehetett a szám?
 

Megoldás: A tizedes vesszőnek egy hellyel való eltolása 10-zel való szorzás vagy osztás, ezért az x:lgx arány értéke vagy 10, vagy 0,1. Az utóbbi lehetőség elesik, mert minden (pozitív) szám 10-es alapú logaritmusa kisebb a számnál. Keressünk x-re közelítő értéket grafikus úton a kapcsolat x/10=lgx alakjából. Az y=x/10 egyenes az y=lgx görbét először az x=1 és x=1,5 abszcisszák között; másodszor pontosan x=10-nél metszi. Valóban, 10 logaritmusa 1,0,‐Péter esetében valószínűleg nem erről a számról van szó. x=1-nél lgx=0<1/10, x=1,5-nél lgx=0,1761>1,5/10=0,15. Hasonlóan lg1,3=0,1139<0,13, lg1,4=0,1461>0,14, tehát 1,3<x<1,4. Tovább finomítva lg1,3713≈0,1371 alapján a keresett szám: x≈1,3713.
 

Fodor Anna (Pécs, Janus Pannonius lg. II. o. t.)
 
Megjegyzés. Hasonló tulajdonságuk van egyrészt a 237,58;3550,2;46692;576040;6834700;78975000;895190000, másrészt az 1,0238;1,C02304 számoknak.
 

Molnár Mária (Sztálinváros, Kerpely A. kohóip. t. l. o. t.)
 

V. Egy lapszéli elmosódott feljegyzésen ez olvasható:
12+(12+22)+(12+22+32)+...+(12+22+32+...+n2)=n(n+1)(n+2)12,
ami nyilván nem igaz, hiszen minden zárójelből csak a legnagyobb tagot véve is többet kapunk a jobb oldali számnál. Ki lehet-e javítani az összefüggést, vagy egészen hibás az?
 

Megoldás: Képezve a bal és jobb oldal hányadosát n=l,2,3-ra a következő értékeket kapjuk: 1:1/2=2; 6:2=3; 20:5=4. Ebből sejtjük, hogy a hányados n+l, és az összefüggést úgy lehet kijavítani, hogy a jobb oldal második tényezőjének (n+l)2-t vesszük. Teljes indukcióval be lehet bizonyítani, hogy így az összefüggés helyes.
 

Bódis Jenő (Veszprém, Vegyip. t. III. o. t.)
 

Legszebben megindokolt dolgozataikért könyvjutalmat kapnak:
Katona Mária (Budapest, Szilágyi E. gyak. lg. l. o. t.),
Bollobás Béla (Budapest, Apáczai Csere J. gyak. g. II. o. t.),
S. Nagy Erzsébet (Makó, József A. g. IV. o. t.).
A vigaszdíjak sorsolásában ‐ a fentiek kivételével ‐ azok vettek részt, akik legalább két megoldást (azaz jó dolgozatot) küldtek be, ki-ki mindegyik dolgozatával. A nyertesek: Kohut Mátyás (Budapest, Apáczai Csere J. gyak. g. III. o.t.),
Palka István (Sátoraljaújhely, Kossuth L. g. II. o. t.),
Pósch Margit (Budapest, Veres Pálné lg. Ill. o. t.).
 

Legalább két megoldást küldtek be (zárójelben a megoldott kérdések száma): Bódis Jenő (2), Böllobás Béla (4), Bornes Klára (2), Fodor Anna (3), Horváth Kálmán (2), Katona Mária (4), Kohut Mátyás (2), Kolonits Ferenc (2), Molnár Mária (2), S. Nagy Erzsébet (3), Palka István (3), Póscb Margit (4), Sarkady Kamilla (2), Szilassi Lajos (2). ‐ Egy megoldást küldött be: 10 tanuló.
*Az eredeti ábrán nem volt betűzés.