Cím:	Az 1966. évi Eötvös Loránd fizikai verseny
Füzet:	1967/február, 81 - 85. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Az 1966. évi Eötvös Loránd fizikai verseny   Az Eötvös Loránd Fizikai Társulat 1966. október 22-én rendezte fizikai versenyét az 1966-ban érettségizettek számára. A versenyzők 5 óráig dolgozhattak és bármilyen segédeszközt használhattak. Az alábbiakban ismertetjük a verseny feladatait és azok megoldását.   1. Vízszintes asztallapon álló, $r=5$ cm rádiuszú, $m=100$ gramm tömegű golyónak nekigurítunk $v_0=280$ cm/s sebességgel egy ugyanilyen golyót. Hogyan folyik le a mozgás? A golyók és az asztallap között a csúszó súrlódási együttható a sebességtől függetlenül $\mu =0\mathrm{,}02$. Az ütközés rugalmatlan, centrális; a golyók közötti súrlódás és a gördülő ellenállás elhanyagolható. $g=1000$cm/s${}^2$. Vizsgáljuk meg az energiaviszonyokat.   Megoldás. Tegyük külön-külön vizsgálat tárgyává a középpontok mozgását és a középpontok körüli forgást. Ütközés előtt az 1. golyó középpontjának $v_0$, a 2. golyó középpontjának 0 a sebessége. Közvetlenül az igen rövid idejű rugalmatlan ütközés után a sebesség megfeleződik, és mindegyik golyó középpontja $v_0/2$ sebességgel halad tovább. Ami a középpontok körüli forgást illeti, ütközés előtt az első golyó olyan szögsebességgel forog, hogy kerületi pontjának sebessége $v_0$, hiszen simán gördül, a 2. golyó kerületi pontjának forgási sebessége pedig 0. Közvetlenül az ütközés után az első golyó kerületi pontja $v_0$ sebességgel forog, de mivel a középpont csak $v_0/2$ sebességgel halad, a kerületi pont túl gyorsan forog, a golyó köszörül. Ezt fékezi a kerületen működő, előre mutató $\mu mg$ súrlódási erő (1. ábra). 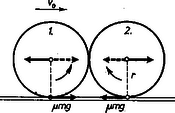    1. ábra   Az 1. golyó középpontjában hozzáveszünk $\pm \mu mg$ erőket. Közülük a bal oldali a súrlódási erővel együtt $\mu mgr$ forgatónyomatékot ad, amely fékezi a forgást. A fékező szöggyorsulás a forgatónyomaték és $I$ tehetetlenségi nyomaték hányadosa: $\beta =\mu mgr/I$, a kerületi pont lineáris gyorsulása $\beta r=\mu mg{r}^2/I$. A középponthoz viszonyított forgás kerületi sebessége lassuló mozgást végez, sebessége: $\begin{array}{c}{\displaystyle v_0-\frac{\mu g}{I/m{r}^2}\cdot t\mathrm{.}}\end{array}$ (1) Ami a 2. golyót illeti, itt a $\mu mgr$ forgatónyomaték gyorsítja a forgást, és a kerületi pont forgási sebessége: $\begin{array}{c}{\displaystyle \frac{\mu g}{I/m{r}^2}\cdot t\mathrm{.}}\end{array}$ (2) A szaggatott vonallal rajzolt $\mu mg$ erők eredője nulla, ezért ezek az erők nem befolyásolják a mozgást. (A golyók közötti súrlódás nulla.) Az első golyó forgásának lassulása, a második golyó forgásának gyorsulása addig tart, amíg a kerületi pont forgási sebessége $v_0/2$ lesz. Akár (1), akár (2) kifejezést tesszük $v_0/2$-vel egyenlővé, a forgás fékeződésének idejére ugyanazt a $\begin{array}{c}{\displaystyle t_0=\frac{v_0}{2\mu g}\cdot \frac{I}{m{r}^2}}\end{array}$ időt kapjuk. Ennyi idő elteltével mindegyik golyó kerületi pontja is $v_0/2$ sebességű lesz, és ezután a golyók simán gurulnak tovább.   A 2. ábra a sebességek időbeli alakulását mutatja. A folytonos vonalak a középpontok haladási sebességeit, a szaggatott vonalak a kerületi pontok forgási sebességeit tüntetik fel.Feladatunk számadatait tekintve a forgás lefékeződésének ideje $t_0=2\mathrm{,}8\text{s}$, ezalatt a golyók középpontjai $\begin{array}{c}{\displaystyle s_0=\frac{v_0}{2}{t}_0=\frac{v_0^2}{4\mu g}\cdot \frac{I}{m{r}^2}=392\text{cm}}\end{array}$ utat tettek meg. (A gömb tehetetlenségi nyomatéka $I=0\mathrm{,}4m{r}^2$.) Sem a lefékeződés ideje, sem útja nem függ a golyók tömegétől és rádiuszától. 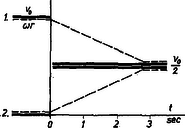    2. ábra   Ütközés előtt az 1. golyónak haladó mozgása miatt 0,5 $m{v}_0^2$, forgása miatt 0,2 $m{v}_0^2$ forgási energiája volt, ez összesen 0,7 $m{v}_0^2$. A 2. golyónak semmiféle mozgási energiája sem volt. (3. ábránkon a haladásból származó mozgási energiát vonalkázás, a forgásból származót pontozás jelzi.)     3. ábra   Közvetlenül az ütközés után a sebesség megfeleződése folytán mindegyik golyó haladó mozgása negyedannyi, 0,125 $m{v}_0^2$ mozgási energiát tartalmaz, de az 1. golyónak megvan az összes forgásból származó mozgási energiája. A végső állapotban mindegyik golyó az eredeti forgásból származó mozgási energia negyedének, 0,05 $m{v}_0^2$-nek birtokába jut, és mindegyikük összes mozgási energiája 0,175 $m{v}_0^2$. Tehát amint az a rugalmatlan ütközésnél szokásos, mozgási energia hővé alakul, éspedig mind a haladási, mind a forgási energia fele. A megmaradt félen osztozik a két golyó.   2. Vákuumban elhelyezett hengeres, egyenes drótot állandó értékű feszültségforrásra kapcsolunk. Ekkor a drót izzó állapotban fényt sugároz ki. Hogyan lehet a drót méretét úgy megváltoztatni, hogy változatlan felvett teljesítmény mellett az összes kisugárzott látható fény mennyisége minél több legyen? A fajlagos ellenállás nem függ a hőmérséklettől. (Károlyházy Frigyes)   Megoldás. Legyen a drót kezdeti hossza $L_0$, kezdeti rádiusza $r_0$, fajlagos ellenállása $k$ és az állandó feszültség $U$. Ekkor a keresztmetszet területe $\pi r_0^2$, az ellenállás $R=k{L}_0/\left(\pi r_0^2\right)$, az áramerősség $I_0=U/R=\pi U{r}_0^2/\left(k{L}_0\right)$ és a felvett teljesítmény $N=U{I}_0=\pi U^2{r}_0^2/\left(k{L}_0\right)$. A drót $r$ rádiusza és $L$ hossza csak úgy változtatható, hogy $N$ állandó maradjon. Ez természetesen azt jelenti, hogy az $R$ ellenállásnak is állandónak kell maradnia (4. ábra).     4. ábra   Ábrázoljuk a drót méreteit meghatározó $r$ rádiuszt és $L$ hosszat $\left(L\mathrm{,}r\right)$ koordináta-rendszerünkben egy-egy ponttal (5. ábra). A koordinátasík minden egyes pontja valamilyen $L\mathrm{,}r$ adatokkal bíró drótméretezést jelent. Tekintettel arra, hogy a teljesítmény állandó, a megengedett $L\mathrm{,}r$ értékpárok az $\begin{array}{c}{\displaystyle r=\sqrt[]{\frac{kN}{\pi U^2}}\cdot \sqrt[]{L}}\end{array}$ fekvő parabola pontjai által vannak meghatározva (folytonos vonal). E fekvő parabola alatti pontok olyan $L\mathrm{,}r$ értékpárokat jelentenek, amelyeknél a drót teljesítményfelvétele kisebb, a parabola felett fekvő pontokban pedig nagyobb, mint a kezdeti $N$. Ábránk arra az esetre vonatkozik, amikor $L_0=40$cm, $r_0=0\mathrm{,}06$cm, $k={10}^{-3}\text{ohm<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>cm}$, $U=177$volt, $N=8850$watt. 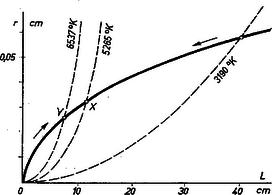    5. ábra   A drótba betáplált egész elektromos teljesítmény sugárzással távozik, a legkülönbözőbb hullámhosszakon. Jelentse $f$ a drót felszínének $1{\text{cm}}^2$ nagyságú területéről az összes hullámhosszakon kisugárzott teljesítményt. Ekkor a drót egész hengeres felszíne az $S=2\pi rL\cdot f$ teljesítményt sugározza ki az összes hullámhosszakon (és ez egyenlő az $N$ betáplált teljesítménnyel). Minket az érdekel, mennyit lát ebből a szem? A szem érzékenysége a ${\lambda }_0=0\mathrm{,}55\mu =5\mathrm{,}5\cdot {10}^{-5}\text{cm}$ körüli keskeny sávra szorítkozik. Az $1{\text{cm}}^2$-ről az összes hullámhosszon kisugárzott energiának csak egy hányada, $f_l$ hasznos a szem számára, és ez biztosan kevesebb, mint $f$: $\begin{array}{c}{\displaystyle f_l=\eta f\mathrm{,}\text{ahol}0<\eta <1.}\end{array}$ Az egész hengeres felszínről a látható hullámhosszakon kisugárzott energia $\begin{array}{c}{\displaystyle S_l=2\pi rL\cdot f_1=\left(2\pi rL\cdot f\right)\eta \mathrm{.}}\end{array}$ Olyan drótméretezést keresünk, amelynél $S_l$ a lehető legnagyobb. Mivel a zárójelben levő mennyiség állandó (egyenlő a felvett teljesítménnyel), az $S_l$ látható teljesítmény csak az $\eta$ hatásfok növelésével javítható. Tehát a válasz úgy szól, hogy olyan $L\mathrm{,}r$ drótméretezés választandó, amely mellett az $1{\text{cm}}^2$-ről kisugárzott teljesítmény minél nagyobb része a $0\mathrm{,}55\mu$ körüli hullámhosszakon kerül kibocsátásra. Ez pedig a hőmérséklettől függ. Az $1{\text{cm}}^2$ felszínről az összes hullámhosszon kisugárzott teljesítmény Stefan‐Boltzmann törvénye szerint az abszolút hőmérséklet negyedik hatványával arányos: $\begin{array}{c}{\displaystyle f=\sigma T^4=5\mathrm{,}68\cdot {10}^{-12}{T}^4\mathrm{,}}\end{array}$ ha a teljesítményt wattban mérjük. Az egész kisugárzott teljesítményt egyenlővé tesszük a betáplált teljesítménnyel: $\begin{array}{c}{\displaystyle 2\pi rL\cdot \sigma T^4=\frac{\pi U^2}{k}\cdot \frac{r^2}{L}\mathrm{,}}\end{array}$ innen az izzószál hőmérséklete: $\begin{array}{c}{\displaystyle T=\sqrt[4]{\frac{U^2}{2k\sigma }}\cdot \sqrt[4]{\frac{r}{L^2}}\mathrm{.}}\end{array}$ Tehát bármely drótméret-adatpár esetében kiszámítható a hőmérséklet. Képletünkből következik, hogy azon $L\mathrm{,}r$ értékpárok, amelyek mellett a drót ugyanazon hőfokú, álló parabolákon vannak: $\begin{array}{c}{\displaystyle r=\frac{2\sigma k{T}^4}{U^2}\cdot L^2\mathrm{.}}\end{array}$ Ezeket az egyező hőmérsékletű drót-méreteket feltüntető parabolákat 5. ábránk szaggatott vonalakkal ábrázolja. Az $L_0=40$cm, $r_0=0\mathrm{,}06$cm kezdeti állapothoz 3190 K tartozik. E parabola alatt hidegebb, fölötte melegebb hőmérsékleteket adó $L\mathrm{,}r$-pontok vannak. A Wien-féle eltolódási törvény szerint a legnagyobb energiával kisugárzott hullámhossz a sugárzó test abszolút hőmérsékletével fordítottan arányos: $\begin{array}{c}{\displaystyle {\lambda }_m\cdot T_m=0\mathrm{,}\mathrm{2896,}}\end{array}$ ha a hullámhosszat cm-ben mérjük. Kézenfekvő gondolat, állapodjunk meg olyan hőmérsékletben, amelyen a 0,55$\mu$-os, szemre legértékesebb hullámhossznál van a maximum. A Wien-törvény szerint ekkor a hőmérséklet 5268 K. Az ehhez tartozó álló parabola az adott teljesítmény fekvő paraboláját $X$ pontban metszi. Tehát az a teendő, hogy drótunk adatait ezen $X$ pont koordinátái szerint válasszuk ($L_m=10\mathrm{,}50$cm, $r_m=0\mathrm{,}0307$cm). Ha a kezdeti adatokat jellemző pont ettől jobbra fekszik, akkor emelni kell a hőmérsékletet, amíg eljutunk $X$-be, ha pedig balra fekszik, akkor csökkenteni kell a hőmérsékletet (mert eredetileg az energiamaximum az ultraibolya felé feküdt). A valóságban a szál nem bír ki ilyen magas hőmérsékleteket, és a fajlagos ellenállás is függ a hőmérséklettől.   Érdekes dolog, hogy az a helyesnek látszó megállapítás, amely szerint a hőfokot úgy kell megválasztani, hogy a maximum a legjobban látható hullámhossz területére essen, kiigazításra szorul. Az $\eta$ hatásfok $f_l$ látható és $f$ összes teljesítmény hányadosa. $f_l$-t a Wien-féle sugárzási törvényből számíthatjuk: $\begin{array}{c}{\displaystyle f_l=\frac{K}{{\lambda }_0^5}{\text{e}}^{-C/\left(T{\lambda }_0\right)}\mathrm{,}}\end{array}$ $f$ pedig a Stefan‐Boltzmann-törvényből ismeretes: $f=\sigma T^4$. Ezek hányadosa a hatásfok: $\begin{array}{c}{\displaystyle \eta =\frac{K}{{\lambda }_0^5}\cdot \frac{{\text{e}}^{-C/\left(T{\lambda }_0\right)}}{\sigma T^4}\mathrm{.}}\end{array}$ E függvény elemzése azt mutatja, hogy a maximuma $T_{mm}=6537$K-nél van. Tehát a 6537 K-hez tartozó álló parabola és a fekvő parabola $Y$ metszéspontját kell megvalósítanunk $L_{mm}=5\mathrm{,}91$cm és $r_{mm}=0\mathrm{,}0231$cm adatokkal. Ekkor a kisugárzott teljesítmény maximuma 0,45 $\mu$-nál van, de a 0,55 $\mu$-ra érzékeny szem számára mégis ez a legkedvezőbb hőmérséklet. A 6. ábra az $\eta$ hatásfok hőmérséklettől függését mutatja. 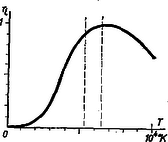    6. ábra   3. Messziről nézzük a Hold vízben tükröződő képét és azt látjuk, hogy eredetileg 0,5${}^{\circ }$-os látószöge függőleges irányban megkétszereződött. A víz felszínén 12 cm hullámhosszúságú hullámok futnak felénk. Mekkora ezek amplitúdója?   Megoldás. Sima víztükör esetén a Hold képét 0,5${}^{\circ }$-os látószöggel látjuk a tükröződés után. Ha a síktükör $\alpha$ szöggel elbillen, akkor a kép $2\alpha$ szöggel billen el. A Hold tükörképének alul-fölül 0,25${}^{\circ }$-os kiszélesedése azt jelenti, hogy a tükröző felszín mindkét irányban 0,125${}^{\circ }$-kal billen ki a vízszintes helyzetéből (7. ábra). A sinus-görbe alakú tükröző felület legmeredekebb része az inflexiós pontokban van, itt kell a szögnek 0,125${}^{\circ }$-nak lennie. Ekkor a $h$ magasság $\begin{array}{c}{\displaystyle h=3\text{cm}\cdot \text{tg}0\mathrm{,}{125}^{\circ }=0\mathrm{,}0129\text{cm.}}\end{array}$ Azonban az amplitúdó ennek a $h$ magasságnak csak $2/\pi$ törtrésze, ezért az amplitúdó $\begin{array}{c}{\displaystyle a=\frac{2h}{\pi }=0\mathrm{,}0083\text{cm}=0\mathrm{,}083\text{mm.}}\end{array}$     7. ábra   A verseny eredménye. I. díjat nyert Rácz Miklós (a Veszprémi Vegyipari Technikumban Burger László és Pulai István tanítványa). Dicséretet kapott Lovász László (a budapesti Fazekas Mihály gimnáziumban Szalay Béla és Wiedemann László tanítványa), Szádeczky Kardoss Gedeon (a budapesti Fazekas Mihály gimnáziumban Szalay Béla tanítványa) és Tüttő Péter (a budapesti Eötvös gimnáziumban Veres Mihályné tanítványa). A versenyen kívül résztvevő középiskolai tanulók közül kitüntető jutalmat kaptak Babai László és Marossy Ferenc (mindketten a budapesti Fazekas Mihály gimnázium III. osztályos tanulói, tanáruk Hutay Ferenc); dicséretet kapott Szalay Sándor (a debreceni Kossuth gyakorló gimnázium IV. osztályában Trón Lászlóné tanítványa).