Kezdőlap


Cím:	A számtani-mértani közép és egyéb érdekességek I.
Szerző(k):	Besenyei Ádám
Füzet:	2009/február, 72 - 80. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Matematikai tanulmányai során mindenki találkozik a számtani és a mértani közép fogalmával. A két közép között fennálló egyenlőtlenség hasznos eszköz például egyszerű szélsőérték-feladatok megoldásában. Bizonyára kevesen gondolnák, hogy a számtani és a mértani közép mellett létezik az úgynevezett számtani-mértani közép is. E dolgozat célja ennek, a magyar nyelvű matematikai szakirodalomban talán kevésbé ismert fogalomnak a rövid bemutatása. Amellett, hogy a számtani-mértani közép egy önmagában is érdekes és egyszerű ,,matematikai objektum'', látni fogjuk, hogy valójában mély matematikai összefüggések rejlenek mögötte. Ezen összefüggések ,,felfedezője'' Gauss volt, eredményei fontos szerepet töltöttek be a matematika egy ágának, az elliptikus függvények elméletének kialakulásában. Természetesen az elliptikus függvények témakörének ismertetése meghaladná e dolgozat kereteit, de a hozzá kapcsolódó történeti háttérre (annak fordulatossága indokán) mindenképpen érdemes kitérnünk. A rövid matematikatörténeti áttekintés mellett dolgozatunkban szót ejtünk az általánosítás és alkalmazás kérdéseiről is, amelyek ugyancsak sok matematikai érdekességet rejtenek. Igyekszünk minden előkerülő fogalmat és állítást több oldalról is megvilágítani, elősegítve ezzel a téma könnyebb megértését. Cikkünk elméleti részében a határérték-számítás elemeire fogunk támaszkodni. Ezzel kapcsolatban a [7] tankönyvre és a [8] példatárra hívjuk fel a figyelmet, amelyekben megtalálhatók a felhasználásra kerülő fogalmak és összefüggések. A történeti háttérről az érdeklődők bővebben olvashatnak az [3] cikkben, a számtani-mértani közép részletes tárgyalását illetően pedig a [2] könyv néhány fejezetét ajánljuk.

Számtani, mértani, számtani-mértani közép

Először röviden elevenítsük fel a számtani és a mértani középpel kapcsolatos ismereteinket.

1. Definíció. Adott

a

b

pozitív valós számok számtani (vagy aritmetikai) közepe

A (a, b) = \frac{a + b}{2}

, mértani (vagy geometriai) közepe

G (a, b) = \sqrt[]{a b}

Jól ismert, hogy bármely

a

b

pozitív valós számok esetén

\begin{matrix} G (a, b) \leq A (a, b), \end{matrix}

(1)

és egyenlőség pontosan akkor áll fenn, ha

a = b

. Ennek bizonyítása kiolvasható az alábbi azonos átalakításból:

\begin{matrix} A (a, b) - G (a, b) = \frac{a + b}{2} - \sqrt[]{a b} = \frac{1}{2} (a - 2 \sqrt[]{a b} + b) = \frac{1}{2} {(\sqrt[]{a} - \sqrt[]{b})}^{2} \geq 0. \end{matrix}

(2)

Érdemes megfogalmaznunk a közepek néhány nagyon egyszerű tulajdonságát. Ehhez vezessük be a következő jelölést:

a

b

valós számok esetén jelölje

{min}_{}^{} (a, b)

és

{max}_{}^{} (a, b)

rendre a két szám közül a kisebbet, illetve a nagyobbat.

2. Állítás. Legyenek

a

b

pozitív valós számok. Ha

M (a, b)

a

b

számok számtani közepe vagy mértani közepe, akkor a következők teljesülnek:

(i)

{min}_{}^{} (a, b) \leq M (a, b) \leq {max}_{}^{} (a, b)

(középérték-tulajdonság),

(i i)

M (a, b) = M (b, a)

(szimmetria),

(i i i)

M (λ a, λ b) = λ M (a, b)

, ahol

λ > 0

tetszőleges (pozitív homogenitás).

Bizonyítás. A közepek definíciója alapján a szimmetria és a pozitív homogenitás nyilvánvaló. A szimmetria miatt feltehető, hogy

a \geq b

, ekkor

\begin{matrix} b = \frac{b + b}{2} \leq \frac{a + b}{2} \leq \frac{a + a}{2} = a, b = \sqrt[]{b b} \leq \sqrt[]{a b} \leq \sqrt[]{a a} = a, \end{matrix}

vagyis teljesül a középérték-tulajdonság.

□

3. megjegyzés. Vegyük észre, hogy ha

(i)

-ben valamelyik egyenlőtlenség egyenlőséggel teljesül, akkor szükségképpen

a = b

(és így mindkét egyenlőtlenségben egyenlőség áll fenn), és megfordítva, ha

a = b

, akkor mindkét helyen egyenlőség teljesül. Erre a tulajdonságra szokás úgy hivatkozni, hogy

M (a, b)

diagonális.

A fenti tulajdonságok szinte nyilvánvalóak, mégis érdemes volt őket külön kiemelni, mert mindegyiket lépten-nyomon (sokszor kimondatlanul) használjuk. Ráadásul az

(i)

tulajdonság megindokolja a közép elnevezést. Másrészt az általános esetben, kettő helyett

n

szám számtani és mértani közepeit tekintve is érvényben maradnak, és például a homogenitás alkalmazható a közepek közötti egyenlőtlenség igazolásában.
Ezek után rátérünk a cikk címében szereplő fogalom bevezetésére. Legyenek

a

b

pozitív valós számok és értelmezzük az

(a_{n})

(b_{n})

sorozatokat a következő rekurzióval (lásd a [8] könyv 48. oldalán a 46. feladatot, illetve a [4] könyv I. kötetének 61‐62. oldalait):

\begin{matrix} a_{0} & : = a & b_{0} : = b & (3) \\ a_{n + 1} & : = \frac{a_{n} + b_{n}}{2} & b_{n + 1} : = \sqrt[]{a_{n} b_{n}} . & (4) \end{matrix}

Más szóval a sorozatok

(n + 1)

-edik tagjai rendre az

n

-edik tagok számtani, illetve mértani közepe, azaz

a_{n + 1} = A (a_{n}, b_{n})

, és

b_{n + 1} = G (a_{n}, b_{n})

4. állítás. Az

(a_{n})

és

(b_{n})

sorozatok konvergensek és ugyanaz a határértékük.

Bizonyítás. Az általánosság megszorítása nélkül feltehető, hogy

a \geq b

, hiszen mind a számtani, mind pedig a mértani közép szimmetrikus, így

a

és

b

felcserélésével a két sorozat nem változik meg. A számtani és a mértani közép között fennálló egyenlőtlenség alapján

b_{n} \leq a_{n}

minden

n \geq 0

esetén, így a középérték-tulajdonság miatt

b_{n} \leq b_{n + 1} \leq a_{n}

és

b_{n} \leq a_{n + 1} \leq a_{n}

, tehát

b_{n} \leq b_{n + 1} \leq a_{n + 1} \leq a_{n}

. Vagyis az alábbi nagyságrendi reláció írható fel:

\begin{matrix} b \leq b_{1} \leq b_{2} \leq ... \leq b_{n} \leq b_{n + 1} \leq ... \leq a_{n + 1} \leq a_{n} \leq ... \leq a_{2} \leq a_{1} \leq a . \end{matrix}

(5)

Ez azt jelenti, hogy

(a_{n})

monoton csökkenő,

(b_{n})

pedig monoton növő sorozat, továbbá mindkettő korlátos. Ismert, hogy ha egy sorozat monoton és korlátos, akkor konvergens (lásd a [7] könyv 159‐163., és a [8] könyv 36‐41. oldalait), így mind

(a_{n})

, mind pedig

(b_{n})

konvergens, határértékük legyen rendre

α

β

. Ekkor a (4) rekurzív definíció miatt a határértékekre

α = \frac{α + β}{2}

és

β = \sqrt[]{α β}

teljesül. Ez viszont (a diagonalitásból következően) azt jelenti, hogy

α = β

□

5. megjegyzés. A bizonyítást a következőképpen is befejezhettük volna. A

(b_{n})

sorozat monoton növekedése folytán

\begin{matrix} 0 \leq a_{n + 1} - b_{n + 1} \leq a_{n + 1} - b_{n} = \frac{a_{n} + b_{n}}{2} - b_{n} = \frac{a_{n} - b_{n}}{2}, \end{matrix}

ahonnan indukcióval kapjuk, hogy

\begin{matrix} 0 \leq a_{n} - b_{n} \leq \frac{1}{2^{n}} (a - b) . \end{matrix}

(a_{n} - b_{n})

sorozatot tehát közrefogtuk két 0-hoz tartó sorozattal, ezért a rendőrelv¹ miatt az

(a_{n} - b_{n})

sorozatnak is 0-hoz kell tartania. Mivel

(a_{n})

és

(b_{n})

külön-külön konvergensek, ezért határértékük szükségképpen megegyezik.

A most bizonyított állítás alapján természetesen adódik a következő fogalom.

6. definíció. Adott

a

b

pozitív számok esetén a (3)‐(4) rekurzióval definiált

(a_{n})

(b_{n})

sorozatok közös határértékét az

a

és

b

számok számtani-mértani közepének nevezzük és a továbbiakban

A G (a, b)

-vel jelöljük. Ezenkívül az

(a_{n})

(b_{n})

sorozatokra a számtani-mértani közepet definiáló sorozatokként hivatkozunk, illetve használjuk a számtani-mértani közép rekurziója (vagy iterációja) elnevezést is.

Könnyen látható, hogy a számtani és a mértani közép tulajdonságai öröklődnek a számtani-mértani középre.

7. állítás. Legyenek

a

b

pozitív valós számok. Ekkor az alábbiak teljesülnek:

(i)

{min}_{}^{} (a, b) \leq G (a, b) \leq A G (a, b) \leq A (a, b) \leq {max}_{}^{} (a, b)

(i i)

A G (a, b) = A G (b, a)

(szimmetria),

(i i i)

A G (λ a, λ b) = λ A G (a, b)

, ahol

λ > 0

tetszőleges (pozitív homogenitás),

(i v)

A G (a, b) = A G (a_{k}, b_{k})

minden

k \geq 0

esetén, ahol

(a_{n})

és

(b_{n})

a

b

számok számtani-mértani közepét definiáló sorozatok (invariancia).

Bizonyítás. A számtani-mértani közép szimmetriája következik a számtani és a mértani közép szimmetriájából, hiszen

a

és

b

felcserélésével az

(a_{n})

(b_{n})

sorozatok nem változnak meg. Hasonlóan, a számtani-mértani közép pozitív homogenitása a számtani és a mértani közép pozitív homogenitásának következménye:

λ a

és

λ b

számtani-mértani közepét definiáló sorozatok éppen

(λ a_{n})

és

(λ b_{n})

, amelyek közös határértéke

λ

-szorosa az

(a_{n})

(b_{n})

sorozatok közös határértékének. Ezenkívül az (5) egyenlőtlenségláncolat alapján az

(i)

,,erős'' középérték-tulajdonság is nyilvánvalóan teljesül, hiszen

a_{1} = A (a, b)

és

b_{1} = G (a, b)

. Végül gondoljuk meg, hogy rögzített

k \geq 0

esetén az

a_{k}

b_{k}

számok számtani-mértani közepét definiáló sorozatok éppen az

(a_{n})

(b_{n})

sorozatok ,,eltoltjai'', vagyis az első

k

tag elhagyásával keletkező sorozatok. A tagok elhagyása a határértéket nem befolyásolja, ezért

A G (a, b) = A G (a_{k}, b_{k})

□

8. megjegyzés. A

(i v)

tulajdonság a

k = 1

speciális esetben azt jelenti, hogy

\begin{matrix} A G (a, b) = A G (A (a, b), G (a, b)) = A G (\frac{a + b}{2}, \sqrt[]{a b}), \end{matrix}

azaz két szám számtani és mértani közepének számtani-mértani közepe megegyezik a két szám számtani-mértani közepével. Más szóval a számtani-mértani közép invariáns a (3)‐(4) rekurzióbeli

(a_{n})

(b_{n})

sorozatokra nézve. Ez az invariancia-tulajdonság a későbbiekben fontos szerepet fog játszani.

1. feladat. Mutassuk meg, hogy a számtani-mértani közép diagonális, sőt, ha az

(i)

egyenlőtlenségláncolatban valahol egyenlőség teljesül, akkor mindenhol egyenlőség áll fenn.

A (3)‐(4) rekurzió (vagy iteráció) kapcsán érdemes egy, az alkalmazások szempontjából igen lényeges tulajdonságra kitérnünk. Mivel egyelőre nincs explicit formulánk két szám számtani-mértani közepére (és hogyha lesz is, ki tudja, hogy azzal vajon könnyen tudunk-e majd számolni), ezért ha kiváncsiak vagyunk két konkrét szám számtani-mértani közepére, akkor nem tehetünk mást, mint az iterációban néhány lépést kiszámolunk. Ekkor várhatóan egy jó közelítést kapunk a számtani-mértani középre. Kérdés, hogy hány lépést végezzünk el (természetesen minél kevesebbet szeretnénk), ha adott tizedesjegynyi pontosságot szeretnénk. Más szóval milyen ,,gyorsan'' fog konvergálni a két sorozat? E kérdés megválaszolásához vegyük észre, hogy (2) miatt

\begin{matrix} a_{n + 1} - b_{n + 1} = \frac{a_{n} + b_{n}}{2} - \sqrt[]{a_{n} b_{n}} = \frac{1}{2} {(\sqrt[]{a_{n}} - \sqrt[]{b_{n}})}^{2}, \end{matrix}

ezért

\begin{matrix} \frac{a_{n + 1} - b_{n + 1}}{{(a_{n} - b_{n})}^{2}} = \frac{1}{2 {(\sqrt[]{a_{n}} + \sqrt[]{b_{n}})}^{2}} . \end{matrix}

A fenti egyenlőség jobb oldalán álló kifejezés konvergens, ezért ,,elég nagy

n

-re közel lesz egy konstanshoz'' (méghozzá

\frac{1}{8 A G (a, b)}

-hez). Azt mondhatjuk tehát, hogy az

(a_{n} - b_{n})

nullsorozat

(n + 1)

-edik tagja az

n

-edik tag négyzetének (nemnulla) konstansszorosával felülről becsülhető. Ilyenkor azt mondjuk, hogy az

(a_{n} - b_{n})

sorozat másodrendben (vagy négyzetesen) konvergál 0-hoz. Durván fogalmazva, minden lépés során megduplázódik a pontos tizedesjegyek száma

(a_{n} - b_{n})

-ben. Ez a négyzetes konvergenciasebesség valójában azt is jelenti, hogy a (3)‐(4) iteráció egy rendkívül gyors és hatékony eljárás a számtani-mértani közép konkrét numerikus kiszámítására, és ennek a későbbi alkalmazások szempontjából nagy jelentősége van.
A (3)‐(4) rekurzió először Joseph-Louis Lagrange (1736‐1813) olasz származású francia matematikus egy 1785-ben megjelent cikkében szerepelt. A közös határérték létezését felhasználva algoritmust dolgozott ki úgynevezett elliptikus integrálok közelítő kiszámítására. Lagrange-tól függetlenül Carl Friedrich Gauss (1777‐1855) 1791-ben, 14 éves korában ,,újrafelfedezte'' a rekurziót. Tőle származik a számtani-mértani közép elnevezés, és ő volt az, aki későbbi vizsgálódásai folyamán észrevette a számtani-mértani közép viszonylag egyszerű fogalma mögött rejlő mély matematikai összefüggéseket, amelyek fontos szerepet töltöttek be az elliptikus integrálok és függvények elméletének kialakulásában. A következőkben röviden bemutatjuk a számtani-mértani középhez vezető út főbb állomásait, majd vázoljuk Gauss eredményeit, és ezzel egyúttal rövid betekintést nyújtunk az elliptikus integrálok elméletébe és annak történetébe.

A Bernoulli-féle lemniszkáta

A történet a 17. század végéig nyúlik vissza, amikor Isaac Newton (1642‐1727) és Gottfried Wilhelm Leibniz (1646‐1716) egymástól függetlenül (és egymástól eltérő szemlélettel) megalapozták és kidolgozták a differenciál- és integrálszámítás elemeit. Az új matematikai eszközöket a kor tudósai többek között a mechanikából származó geometriai jellegű problémák megoldására próbálták alkalmazni. Általában olyan görbék meghatározása volt a feladat, amelyeket egy adott ,,részecske'' bizonyos kényszererők hatására leír. Talán az egyik legismertebb a Johann Bernoulli (1667‐1748) svájci matematikus által felvetett brachisztochron probléma: határozzuk meg azt a görbét, amely mentén (súrlódásmentes esetet feltételezve) egy golyó az állandó nehézségi erő hatására a leggyorsabban legurul. Johann és testvére, Jakob Bernoulli (1654‐1705) rengeteg hasonló kérdést vetett fel és tanulmányozott. Az isochrona paracentrica probléma a következő volt: melyik az a görbe, amely mentén leguruló test egyenlő időközök alatt egyenlő utakat tesz meg. E probléma vizsgálata során jutott el Jakob 1694-ben az alábbi egyenlethez:

\begin{matrix} {(x^{2} + y^{2})}^{2} = 2 a^{2} (x^{2} - y^{2}) . \end{matrix}

(6)

Jakob a görbét egy ,,elfordított nyolcashoz'' hasonlította és lemniscusnak nevezte el, amely görögül szalagot jelent. A fenti egyenlettel meghatározott görbét, amelyet (Bernoulli-féle) lemniszkátának szokás hívni az 1. ábra szemlélteti.

2. feladat. Írjuk fel a lemniszkáta polárkoordinátás egyenletét, azaz végezzük el az

x = r cos φ

y = r sin φ

helyettesítést, ahol

r \geq 0

0 \leq φ < 2 π

, majd ellenőrizzük az 1. ábrán a görbe alakjának helyességét.

Valójában ez a görbe már néhány évvel korábban ismert volt. Giovanni Domenico Cassini (1625‐1712) olasz matematikus és csillagász a Nap és a Föld egymáshoz viszonyított mozgásának tanulmányozása során 1680-ban a később róla elnevezett Cassini-féle oválisokat vizsgálta. Úgy gondolta, hogy a Nap a Föld körül egy olyan ovális pályán kering, amelynek két, egymástól

2 a

távolságra lévő fókuszpontja van (az egyikben éppen a Föld helyezkedik el) és a pálya mentén lévő pontok két fókuszponttól mért távolságainak szorzata állandó (

b^{2}

3. feladat. Mutassuk meg, hogy az

a = b

speciális esetben a Cassini-féle ovális éppen a Bernoulli-féle lemniszkáta. Más szóval, azon pontok mértani helye a síkon, amelyeknek az egymástól

2 a

távolságra lévő

(- a,0)

és

(a,0)

fókuszpontoktól mért távolságainak szorzata

a^{2}

, a (6) egyenlettel leírt lemniszkáta.

Jegyezzük meg, hogy ha a két fókuszponttól mért távolságok szorzata helyett a távolságok összegét követeljük meg állandónak, akkor egy ellipszist kapunk (amelynek fogalmát Menaikhmosz görög matematikus már i.e. 350 körül bevezette).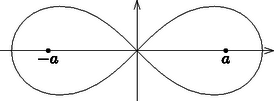

1. ábra

Térjünk most vissza az említett mechanikai-geometriai jellegű feladatokhoz. Az alkalmazások miatt e problémák tanulmányozása nemcsak a testek mozgását leíró görbék egyenletének felírását jelentette, hanem ezen túlmenően fontos kérdés volt a görbék tulajdonságainak vizsgálata is, többek között az ívhosszuk meghatározása. A lemniszkáta ívhosszára Jakob Bernoullinak sikerült egy formulát felírnia. Az egyszerűség kedvéért a (6) egyenletben válasszuk az

a

paraméter értékét

\frac{1}{\sqrt[]{2}}

-nek, ekkor a lemniszkáta pozitív síknegyedbe eső darabjának hossza²:

\begin{matrix} \int_{0}^{1} \frac{d t}{\sqrt[]{1 - t^{4}}} . \end{matrix}

(7)

A fenti integrált elsőfajú teljes elliptikus integrálnak hívjuk (a teljesség az integrálás határaira utal). Általában elsőfajú elliptikus integrálnak az

\begin{matrix} F (x) = \int_{0}^{x} \frac{d t}{\sqrt[]{(1 \pm p^{2} t^{2}) (1 \pm q^{2} t^{2})}} \end{matrix}

(8)

alakú függvényeket nevezzük, ahol

p, q

pozitív számok (és a

\pm

előjelek bármely párosítása választható). Az ilyen típusú függvények inverzeit hívjuk elliptikus függvényeknek. Megjegyezzük, hogy a (7) integrál nemcsak a korábban említett isochrona paracentrica feladat kapcsán, hanem már 1691-ben előkerült Jakobnál az úgynevezett elasztikus görbe ívhosszának tanulmányozása során: milyen alakot vesz fel egy rugalmas rúd, amelyre mindkét végén összenyomó erő hat?
A lemniszkáta történetéhez mindenképpen meg kell említenünk, hogy Johann Bernoullinak, testvérétől függetlenül, ugyancsak sikerült felírnia a (6) egyenletet az isochrona paracentrica probléma megoldása során. Johann cikke azonban egy hónappal később jelent meg, mint Jakobé, ezzel elsőbbségi vitát kiváltva az amúgy is egymással versengő fivérek között.
A Bernoulli fivérek munkáit követően Giulio Carlo Fagnano (1682‐1766) olasz matematikus (aki egyébként később hercegi címet is kapott) folytatta a lemniszkáta ívhosszához (és a (7) alakú integrálhoz) kötődő kérdések tanulmányozását. Fagnano fő eredménye a lemniszkáta ,,ívének megkétszerezése'' volt. Sikerült algebrai műveletek segítségével meghatároznia, hogy milyen hosszú a lemniszkátának azon (origóból induló) húrja, amelyhez kétszer akkora lemiszkátaív tartozik, mint a

t

hosszúságú húrhoz. Nevezetesen, ha

\begin{matrix} u = \frac{2 t \sqrt[]{1 - t^{4}}}{1 + t^{4}}, \end{matrix}

(9)

akkor az

u

hosszúságú húrhoz kétszer akkora ív tartozik, mint a

t

hosszúságú húrhoz, lásd a 2. ábrát. A (9) képlet jelentősége abban rejlik, hogy a jobb oldalán szereplő kifejezés

t

ismeretében vonalzóval és körzővel megszerkeszthető, így a lemniszkáta egy ívének megkétszerezése is elvégezhető ezen eszközök segítségével.

2. ábra

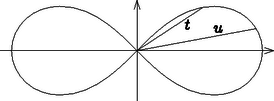Ezt követően Fagnanonak sikerült eljárást kidolgoznia lemniszkátaívek

n

egyenlő részre osztására, ahol

n = 2^{m}

n = 3 \cdot 2^{m}

vagy

n = 5 \cdot 2^{m}

alakú lehet. Eredményeit először egy kevéssé ismert folyóiratban közölte 1714 és 1720 között. Később, 1750-ben újra megjelentette munkáit és elküldte azokat a Berlini Tudományos Akadémiának, amelynek tagságára pályázott. Az Akadémia Leonhard Eulert (1707‐1783) kérte fel Fagnano munkáinak átnézésre. Euler (aki Johann Bernoulli tanítványa volt) a Bernoulli testvérek munkái nyomán már 1728-tól kezdődően foglalkozott az elasztikus görbével és általában rugalmasságtani problémákkal, továbbá az ellipszis ívhosszával kapcsolatos kérdésekkel. E témakörök mindegyike az elliptikus integrálok vizsgálatához vezettek. (Ha ugyanis a (8) integrálban a

- \frac{1}{2}

kitevőt

\frac{1}{2}

-re cseréljük, akkor a másodfajú elliptikus integrálokat kapjuk, amelyek többek között az ellipszis ívhosszához kapcsolódó problémákban fordulnak elő.)
Fagnano eredményei új lendületet adtak Euler korábbi vizsgálódásainak. A Fagnano-féle ,,ívkétszerezés'' mintájára, azt lényegesen általánosítva úgynevezett addíciós formulát dolgozott ki, először (7), később pedig (8) alakú elliptikus integrálokra, és mindezt 1761-ben publikálta. Ezután további jelentős eredményeket ért el és ezzel megtette az első lépéseket az elliptikus integrálok elméletének kidolgozása felé. Ennek kapcsán Euler egy gyönyörű formuláját mindenképpen érdemes megemlítenünk:

\begin{matrix} \int_{0}^{1} \frac{d t}{\sqrt[]{1 - t^{4}}} \cdot \int_{0}^{1} \frac{t^{2}}{\sqrt[]{1 - t^{4}}} d t = \frac{π}{4} . \end{matrix}

(10)

A fenti szorzatban szereplő első integrál, mint láttuk, a lemniszkáta ívhossza, a második integrál pedig az elasztikus görbével áll szoros kapcsolatban.
Eredményeivel Euler megalapozta az elliptikus integrálok elméletét, amelyet később Adrien-Marie Legendre (1752‐1833) dolgozott ki klasszikus formában és 1826-ban kétkötetes monográfiában jelentetett meg. Ezt követően Niels Henrik Abel (1802‐1829) norvég és Carl Gustav Jacob Jacobi (1804‐1851) porosz matematikusok (mindkettejük mentora Legendre volt) teljesen új megvilágításba helyezték az addigi elméletet. Ők az elliptikus integrálok inverzeit tanulmányozták és ezáltal bontakozott ki az elliptikus függvények modern elmélete. Munkáik jelentőségét (és Legendre nagyságát) mutatja, hogy Legendre egy harmadik kötettel egészítette ki monográfiáját, abban ismertetve Abel és Jacobi eredményeit.
A történethez hozzátartozik, hogy Fagnano akadémiai pályázatát Euler természetesen támogatta, így a Berlini Tudományos Akadémia tagjává választotta. Jacobi 1751. december 23-át, amikor is Euler megkapta Fagnano munkáit, a ,,matematika történetének egyik rendkívül fontos napjának'' nevezte.
Fagnano munkásságát illetően ajánljuk az [1] cikket, továbbá felhívjuk a figyelmet a [6] dolgozatra, amelyben a lemniszkátának és az elliptikus integráloknak a harmadrendű görbékkel való kapcsolatáról olvashatnak az érdeklődők. A brachisztochron problémáról, valamint Lagrange, Euler és Gauss életéről és munkásságáról további részleteket a kiváló [5] műben találhat az Olvasó. Végül érdemes megemlíteni, hogy Giulio Fagnano fia, Giovanni Francesco Fagnano (1715‐1797) ugyancsak beírta a nevét a matematika történetébe, ugyanis tőle származik a Fagnano-féle probléma: hegyesszögű háromszögbe írható háromszögek közül melyiknek lesz minimális a kerülete?

Irodalom

[1]	Ayoub, R., The Lemniscate and Fagnano's Contributions to Elliptic Integrals, Arch. Hist. Exact Sci., 29 (1984), 131‐149.

[2]	Borwein, J. M. ‐ Borwein, P. B., Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, John Wiley (New York, 1987).

[3]	Cox, D. A., The Arithmetic-Geometric Mean of Gauss, L'Ensign. Math., 30 (1984), 275‐330.³

[4]	Fichtenholz, G. M., Differential- und Integralrechnung I‐II, VEB Deutscher Verlag der Wissenschaften (Berlin, 1964).

[5]	Gingyikin, Sz. G., Történetek fizikusokról és matematikusokról, TYPOTeX Kiadó (Budapest, 2003).

[6]	Hraskó András, Poncelet tétele, KöMaL, 2005/5, 264‐275.

[7]	dr. Pintér Lajos, Analízis I. (a gimnázium speciális matematika osztályai számára), Tankönyvkiadó (Budapest, 1987).

[8]	Urbán János, Határérték-számítás, Műszaki Könyvkiadó (Budapest, 1975).

¹A rendőrelv (vagy csendőrelv) szerint, ha

(x_{n})

(y_{n})

(z_{n})

olyan számsorozatok, amelyekre

x_{n} \leq y_{n} \leq z_{n}

, továbbá

x_{n} \to x

és

z_{n} \to x

, akkor szükségképpen

y_{n} \to x

. Tréfásan fogalmazva, ha

x_{n}

és

z_{n}

két ,,rendőr'' és

y_{n}

a ,,letartóztatott'', akkor

y_{n}

kénytelen ,,oda tartani'', ahova a két ,,rendőr'' tart. Lásd a [7] könyv 143‐145. oldalait és a [8] könyv 31. oldalán a 10. feladatot.

²Mivel ebben és a következő szakaszban csak a történeti háttér ismertetésére törekszünk, ezért az előkerülő formulákat bizonyítás nélkül közöljük, a részleteket illetően lásd például az [3] cikket vagy a [4] könyv II. kötetének 144‐147. és 184‐185. oldalait.

³A cikk digitalizált változata elérhető a svájci elektronikus akadémiai könyvtár rendszerén, a http://retro.seals.ch oldalon.