Kezdőlap


Cím:	Kunfalvi Rezső fizikai diákolimpiai válogatóverseny
Füzet:	2008/november, 499 - 504. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elméleti feladatok

1. Egy

α

hajlásszögű lejtő

l

hosszúságú. A lejtő tetejére egy kisméretű hasábot helyezünk, amit kezdősebesség nélkül elengedünk. A hasáb és a lejtő felszíne között a csúszási súrlódási együttható

μ < \frac{tg α}{2}

$a)$	Határozzuk meg, hogy mennyi idő alatt éri el a lejtő alját a test!

$b)$	Határozzuk meg, hogy mekkora sebességgel éri el a lejtő alját a test!

Ezután a lejtő felületén úgy változtatunk, hogy a súrlódási együttható 0 értékről indulva, a lejtő hossza mentén egyenletesen növekedve, a lejtő alján

2 μ

értéket érjen el.

$c)$	Az előző esethez képest hosszabb vagy rövidebb idő alatt éri el a test a lejtő alját?

$d)$	Az előző esethez képest kisebb vagy nagyobb sebességgel éri el a test a lejtő alját?

$e)$	Határozzuk meg, hogy ebben az esetben mennyi idő alatt éri el a test a lejtő alját!

$f)$	Határozzuk meg, hogy ebben az esetben mekkora sebességgel éri el a test a lejtő alját!

Ezt követően megfordítjuk a lejtő felületét alkotó lemezt, tehát most a lejtő tetején a súrlódási együttható

2 μ

, ami a lejtő hossza mentén egyenletesen 0 értékre csökken.

$g)$	Az előző két esethez képest hosszabb vagy rövidebb idő alatt éri el a lejtő alját a test?

$h)$	Az előző két esethez képest kisebb vagy nagyobb sebességgel éri el a lejtő alját a test?

$i)$	Határozzuk meg, hogy ebben az esetben mennyi idő alatt éri el a lejtő alját a test!

$j)$	Határozzuk meg, hogy ebben az esetben mekkora sebességgel éri el a lejtő alját a test!

A számításokat végezzük el paraméteresen! Határozzuk meg a numerikus végeredményeket is a következő adatok segítségével:

g = 9, 8 m/s^{2}

α = 30^{\circ}

l = 1

μ = 0, 2

.
Abban az esetben, ha valaki úgy érzi, hogy a paraméteres számolás túlságosan hosszú vagy reménytelenül nehéz számára, arányosan csökkentett pontszámért számolhat numerikusan is.

2. A világűr egy távoli részén, ahol még a gravitáció is elhanyagolható, ámde a vákuum tökéletes, egy

M

tömegű, egyik végén zárt, másik végén nyitott henger alakú tartály található. A henger közepén egy

m

tömegű, elhanyagolható vastagságú dugattyú osztja két egyenlő részre a henger térfogatát. A henger elzárt részében

n

mól egyatomos gáz van, melynek moláris tömege

M_{0}

és hőmérséklete

T

. Amint feloldjuk a dugattyú rögzítését, a dugattyú súrlódásmentesen elhagyja a hengert.

$a)$	Mekkora a tartály sebessége, amikor a dugattyú a tartály végére ér?

Ebben a pillanatban a dugattyú leválik a rendszerről, és a továbbiakban a dugattyúval nem kell foglalkoznunk. Ezt követően a gáz is elhagyja a tartályt.

$b)$	Közelítő számítás segítségével határozzuk meg, hogy mekkora lesz a tartály végső sebessége.

Útmutatás az

a)

és a

b)

alkérdések megoldásához: A gáz tömege sokkal kisebb, mint a dugattyú tömege, továbbá a dugattyú tömege kisebb, mint a tartály tömege:

n M_{0} ≪ m < M

. A gáz, a tartály és a dugattyú között mindenféle hőcserétől eltekinthetünk. Ugyancsak eltekinthetünk a gáz hőmérsékletváltozásától, amikor a gáz a dugattyú kilökődése után elhagyja a tartályt. A számításunkat végezzük el paraméteresen.

$c)$	Adjuk meg számszerűen is a tartály végső sebességét a következő adatok segítségével: $M = 2$ kg, $m = 1$ kg, $n = 2$ mol, $M_{0} = 40$ g/mol, $T = 300$ K, $R = 8, 31 J/mol\cdotK$ .

$d)$	Hogyan változik (nő, csökken, nem változik) a gáz entrópiája az $a)$ és a $b)$ folyamat során?

3. Egy pozitív és egy ugyanakkora nagyságú negatív ponttöltésből álló alakzatot elektromos dipólusnak nevezünk. A dipólust a negatív töltésből a pozitív töltésbe mutató vektorral, az úgynevezett dipólmomentummal jellemezzük, amit

p

-vel jelölünk. Ha a dipólust alkotó töltések

+ q

és

- q

értékűek, és a közöttük lévő távolság

d

, akkor a dipólmomentum nagysága:

q d

. A dipólust pontszerűnek nevezzük, ha

d ≪ r

, ahol

r

-rel jelöljük a vizsgált jelenségben tipikus távolságokat, amit a dipólus középpontjától mérünk. Helyezzük a koordináta-rendszerünk origóját a dipólus középpontjába, így a dipólus körüli tér tetszőlegesen megválasztott pontját az

r

helyvektorral jellemezzük.

a)

Határozzuk meg a pontszerűnek tekinthető,

p

dipólmomentumú dipólus körül az elektromos potenciál értékét egy tetszőleges

r

pontban! A potenciált fejezzük ki a dipólmomentumtól mért

r

távolság, a dipólmomentum

p

abszolút értéke, valamint a

p

és

r

vektorok közötti

α

szög segítségével! (Ismeretes, hogy a vákuum

ε_{0}

dielektromos állandója a következő módon fejezhető ki a Coulomb-törvényben szereplő

k = 9 \cdot 10^{9} \frac{Nm^{2}}{C^{2}}

állandóval:

k = \frac{1}{4 π ε_{0}}

.)
Tekintsük a rögzített, pontszerű elektromos dipólus szimmetriasíkját. (A

p

dipólmomentum merőleges erre a síkra.) Helyezzünk el egy

Q

ponttöltést ezen a síkon a dipólustól

r ≫ d

távolságban.

$b)$	Mekkora erő hat a ponttöltésre? A választ $p$ , $r$ és $Q$ segítségével fejezzük ki!

A pontszerű dipólust továbbra is tartsuk rögzítve, azonban a dipólus szimmetriasíkjában nyugvó

Q

ponttöltést kezdősebesség nélkül engedjük szabadon mozogni. A ponttöltés tömege olyan kicsi, hogy a gravitációs erőtől eltekinthetünk. A kísérletet elvégezve azt tapasztaljuk, hogy a ponttöltés körpályán mozog.

$c)$	Bizonyítsuk be elméletileg, hogy a ponttöltés pályája kör! (A bizonyításhoz nem szükséges a ponttöltés mozgásegyenletét megoldanunk.)

$d)$	A szabadon engedett ponttöltés megáll-e valahol a körpályán? Ha igen, adjuk meg az elengedést követő első megállás helyét!

4. Vizsgáljunk egy vékony,

2 l

hosszúságú fémrudat, például bicikli küllőt. A küllőt forgassuk meg a középpontján átmenő, a hosszára merőleges tengely körül

ω

szögsebességgel. Helyezzük a küllőt a forgástengellyel párhuzamos

B

indukciójú, homogén mágneses térbe.

$a)$	Milyen elektrosztatikus mező alakul ki a küllő belsejében, ha a küllőt viszonylag lassan forgatjuk, ezért az elektronok tehetetlenségéből adódó járuléktól eltekinthetünk?

$b)$	Milyen elektrosztatikus mező alakul ki a küllő belsejében, ha a forgás gyorsabb, ezért nem hanyagolhatjuk el az elektronok tehetetlenségéből adódó járulékot?

$c)$	Milyen térfogati töltéseloszlás jön létre a küllő belsejében, ha a küllőt viszonylag lassan forgatjuk, ezért az elektronok tehetetlenségéből adódó járuléktól eltekinthetünk?

$d)$	Milyen térfogati töltéseloszlás jön létre a küllő belsejében, ha a forgás gyorsabb, ezért nem hanyagolhatjuk el az elektronok tehetetlenségéből adódó járulékot?

$e)$	Mekkora szögsebesség esetén képzelhető el, hogy a töltéssűrűség a küllő bizonyos pontjaiban nulla legyen?

$f)$	Ilyen szögsebesség esetén határozzuk meg a küllő összes nulla töltéssűrűségű pontjának a henger szimmetriatengelyétől mért távolságát!

g)

Ha az előző két kérdésre sikerült válaszolnunk, akkor válasszunk ki egy ilyen pontot, és számítsuk ki számszerűen azt a szögsebességet, amely nulla töltéssűrűséget eredményez! Numerikus adatok:

B = 3 \cdot 10^{- 5}

T (a földi mágneses tér), a küllő hossza

2 l = 30

cm,

e = - 1, 6 \cdot 10^{- 19}

m_{e} = 9, 1 \cdot 10^{- 31}

kg.

Ezek után oldjuk meg a feladatot úgy is, hogy nem küllőt, hanem egy

R

sugarú fémhengert forgatunk meg az alkotóival párhuzamos szimmetria tengelye körül. A szögsebesség legyen olyan lassú, hogy az elektronok tehetetlenségéből adódó járuléktól eltekinthetünk.

$h)$	Ugyanolyan térfogati töltéseloszlás jön létre a hengerben, mint amilyet a $c)$ kérdésre adott válaszban kaptunk?

$i)$	Ha az előző alkérdésre adott válaszunk igen, akkor bizonyítsuk az állításunkat! Ha az előző alkérdésre adott válaszunk nem, akkor számítsuk ki, hogy milyen lesz a hengerben kialakuló térfogati töltéssűrűség!

5. feladat: Az ábrán látható összeállításban a csiga tehetetlensége és a súrlódás elhanyagolható. A rendszert nyugalmi helyzetből indítjuk. Határozzuk meg, hogy milyen

α

szögek esetén emelkedik fel a

m

tömegű test a vízszintes asztalról közvetlenül az elindítás után! Vizsgáljuk meg a

M ≫ m

esetet is, és mondjuk meg, hogy nevezzük ebben a határesetben a

sin α_{határ}

számot!

6. feladat: Az A és a B jelű folyadékok nem oldódnak egymásban. Telített gőznyomásukat (amit így jelölünk:

p_{i}

, ahol

i = A

vagy B) jó közelítéssel a következő összefüggéssel írhatjuk le:

\begin{matrix} ln (p_{i} / p_{0}) = \frac{α_{i}}{T} + β_{i}; i = A vagy B, \end{matrix}

ahol

p_{0}

jelöli a normál légköri nyomást,

T

a gőz abszolút hőmérsékletét, továbbá

α_{i}

és

β_{i}

(

i = A

vagy B) a folyadéktól függő állandók.
A

p_{i} / p_{0}

arány értékét

40^{\circ}

C és

90^{\circ}

C hőmérsékletek esetén az 1. táblázat tartalmazza az A és B folyadékra:

1. táblázat

\begin{matrix} p_{i} / p_{0} \\ t[^{\circ}C] & i = A & i = B \\ 40 & 0,284 & 0,07278 \\ 90 & 1,476 & 0,6918 \end{matrix}

Ezeknek az értékeknek a hibái elhanyagolhatóak.

A .

Határozzuk meg az A és B folyadék forráspontját

p_{0}

nyomás esetén!

B .

Az A és B nem-keveredő folyadékot rétegezve egy edénybe öntjük, amint ez az 1. ábrán látható. A B folyadék felszínét a C jelű nem-párolgó folyadék vékony rétegével borítjuk be, amely nem oldódik sem az A, sem a B folyadékban, illetve ez megfordítva is igaz, az A és a B folyadék sem oldódik C-ben. Ezzel megakadályozzuk a B folyadék felső felszínéről történő bármiféle szabad párolgást. Az A és a B folyadék moláris tömegének aránya:

\begin{matrix} γ = μ_{A} / μ_{B} = 8. \end{matrix}

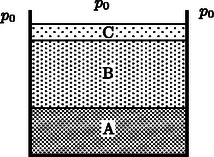1. ábra

Az A és a B folyadék tömege kezdetben megegyezik, mindkettő

m = 100

g. A folyadékszintek magassága az edényben, illetve a folyadékok sűrűsége elegendően kicsiny ahhoz, hogy jó közelítéssel úgy tekinthetjük, az edény belsejében minden pontban a nyomás megegyezik a

p_{0}

normál légköri nyomással.
A folyadékokból álló rendszert lassan, folyamatosan és egyenletesen melegítjük. A folyadékok

t

hőmérsékletének változását a

τ

idő függvényében a 2. ábra mutatja vázlatosan.

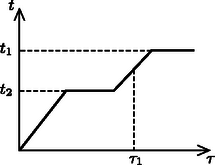2. ábra

Határozzuk meg a

t_{1}

és

t_{2}

hőmérsékleteket, melyek a grafikon vízszintes szakaszaihoz tartoznak, továbbá számítsuk ki az A és B folyadék tömegét a

τ_{1}

időpontban. A hőmérsékleteket kerekítsük (

^{\circ}

C-ban) a legközelebbi egész értékre, a folyadékok tömegét pedig adjuk meg tized-gramm pontossággal!
Megjegyzés: Tételezzük fel, hogy a folyadékok gőzeire jó közelítéssel

(1)	teljesül a Dalton-törvény, ami azt állítja, hogy a keverék gázok nyomása megegyezik a keveréket alkotó gázok parciális nyomásainak összegével, továbbá

(2)	a folyadékok gőzeit ideális gázként kezelhetjük a feladatban előforduló nyomások esetén.

(

0^{\circ} C = 273, 15

K.)

7. feladat: Az

m_{1}

m_{2}

és

m_{3}

különböző tömegű tömegpontok a

P_{1}

P_{2}

és

P_{3}

nem egy egyenesbe eső pontokban helyezkednek el. A három tömegpont csak a gravitációs erőkkel hat kölcsön egymással; mindentől távol, az üres térben vannak, más testekkel nincs kölcsönhatásuk. Jelölje

σ

a három tömegpont tömegközéppontján átmenő tengelyt, amely merőleges a

P_{1} P_{2} P_{3}

háromszögre. Milyen feltételeknek kell teljesülniük a rendszer

σ

tengely körüli

ω

szögsebességére, továbbá a

\begin{matrix} P_{1} P_{2} = a_{12}, P_{2} P_{3} = a_{23}, P_{1} P_{3} = a_{13}, \end{matrix}

távolságokra, hogy a

P_{1} P_{2} P_{3}

háromszög alakja és mérete a rendszer mozgása közben ne változzon, vagyis milyen feltételek esetén fog a rendszer a

σ

tengely körül merev testként forogni?

8. feladat: Ez a feladat egy elektronmikroszkóp protonmikroszkóppá történő átalakításának vizsgálatával foglalkozik. A vizsgált elektronmikroszkópban az

U = 511

kV feszültséggel gyorsított elektronnyalábot mágnesesen vezérlik. Az átalakított protonmikroszkópban a protonnyalábot

- U

feszültség gyorsítja. A feladatban a következő két problémát kell megoldanunk:

A .

Egy elektron, miután elhagyja az elektronágyút, vagyis azt az eszközt, amely

U

feszültséggel gyorsította, egy olyan térrészbe érkezik, ahol a

B

mágneses mező inhomogén. A mágneses mezőt az

L_{1}, L_{2}, ..., L_{n}

stacionárius (időben nem változó) tekercsrendszer állítja elő, melyek áramai rendre

i_{1}, i_{2}, ..., i_{n}

értékűek.
Milyenek legyenek az

i_{1}', i_{2}', ..., i_{n}'

áramok az

L_{1}, L_{2}, ..., L_{n}

tekercsekben, hogy az előzőleg

- U

feszültséggel gyorsított proton ugyanazt a pályát fussa be, mint az elektron?
Útmutatás. A feladatot meg lehet oldani úgy, ha találunk egy feltételt, melynek teljesülése esetén a pályát leíró egyenlet mindkét esetben ugyanaz. Segítségünkre lehet a következő összefüggés használata:

\begin{matrix} p \frac{d}{d t} p = \frac{1}{2} \frac{d}{d t} p^{2} = \frac{1}{2} \frac{d}{d t} p^{2} . \end{matrix}

B .

Hányszorosára növekedne vagy csökkenne a fenti mikroszkóp felbontóképessége, ha az elektronnyalábot protonnyalábra cseréljük? Tegyük fel, hogy a mikroszkóp felbontóképessége (vagyis két pontszerű tárgy közötti legkisebb távolság, amit meg tudunk különböztetni) csak a részecskék hullámtulajdonságaitól függ.
Feltételezhetjük, hogy az elektronok és a protonok gyorsítás előtti sebessége zérus, továbbá, hogy az elektronok és a protonok saját mágneses nyomatéka és a mágneses mező között nincs kölcsönhatás. Tegyük fel azt is, hogy a mozgó részecskék elektromágneses sugárzása elhanyagolható.
Adatok:

\begin{matrix} Az elektron nyugalmi energiája: & E_{e} = m_{e} c^{2} = 511keV, \\ A proton nyugalmi energiája: & E_{p} = m_{p} c^{2} = 938MeV. \end{matrix}

(

1 eV = 1, 6 \cdot 10^{- 19}

c = 3 \cdot 10^{8}

m/s.)

¹A versenyen ‐ két fordulóban ‐ összesen 8 elméleti és 3 mérési feladat szerepelt; itt most ‐ terjedelmi okokból ‐ az elméleti problémákat ismertetjük.