Kezdőlap


Cím:	A 39. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Honyek Gyula , Tasnádi Tamás
Füzet:	2008/november, 488 - 498. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. ,,Vízzel hajtott rizshántoló mozsár''

1. A mozsár felépítése
1.1. A

T G

távolság kiszámítása. A kanálban összegyűlt 1 liter víz forgatónyomatéka egyensúlyt tart az emelőrúd súlyából származó forgatónyomatékkal. Geometriai megfontolásokból kiszámíthatjuk, hogy 1 liter víz esetén a kanálban a vízmagasság 1,2 cm, és ennek a vízmennyiségnek a súlypontja nagyjából 47 cm-re van a

T

forgástengelytől. Mivel az emelőrúd tömege 30-szor nagyobb 1 liter víz tömegénél, így a kérdéses

T G

távolság

\begin{matrix} \frac{47}{30} cm = 1, 57 cm \approx 1, 6 cm . \end{matrix}

1.2. Az

α_{1}

és

α_{2}

értékek kiszámítása. Amikor az emelőrúd

α_{1}

dőlésszögénél a víz eléri a kanál peremét, akkor az 1. ábrán látható helyzetet veszi fel. Ekkor a kanálban lévő 1 liter víz egy háromszög alapú egyenes hasábot tölt ki, melynek térfogatát könnyen felírhatjuk:

V = \frac{h b (P Q)}{2} = 1

liter, ahol

b = 15

cm a kanál szélessége. A számítás

P Q \approx 11, 1

cm eredményre vezet.

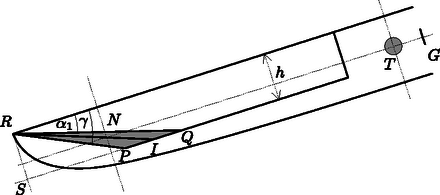1. ábra

Az emelőrúd

α_{1}

dőlésszögét így számíthatjuk ki:

\begin{matrix} tg α_{1} = \frac{h}{S Q} = \frac{h}{P Q + \sqrt[]{3} h}, \end{matrix}

amiből

α_{1} = 20, 6^{\circ}

.
A kanálból akkor távozik az összes víz, ha az emelőrúd dőlésszöge:

α_{2} = γ = 30^{\circ}

.
1.3. A nulla forgatónyomatékhoz tartozó

β

szög és

m_{1}

víztömeg kiszámítása. Használjuk újra az előző ábrát, és ahol csak lehet, írjuk be a képletekbe a numerikus értékeket. Jelöljük a

P Q

távolságot

x

-szel, amit mérjünk méterben:

P Q = x

(m), amivel így adhatjuk meg a kanálban maradó víz

m

tömegét kilogrammban:

m = ϱ_{víz} \frac{x h b}{2} = 9 x

(kg). A víz súlypontja a

P Q R

háromszög súlypontjában van, az

R I

súlyvonal

2 / 3

részénél. A szerkezet geometriai elrendezéséből következik, hogy az emelőrúd

G

súlypontja, a

T

forgástengely (középpontja) és a kanálban maradó víz

N

súlypontja egy egyenes mentén helyezkedik el. A forgatónyomaték egyensúlyt így írhatjuk fel:

\begin{matrix} m g \cdot T N = M g \cdot T G \Rightarrow m \cdot T N = M \cdot T G = 30 \cdot 0, 0157 = 0, 471 (kgm). \end{matrix}

T N

távolságot így írhatjuk fel:

\begin{matrix} T N = L + a - \frac{2}{3} (\sqrt[]{3} h + \frac{x}{2}) = 0, 94 - 0, 08 \sqrt[]{3} - \frac{x}{3} = 0, 801 - \frac{x}{3} . \end{matrix}

Az eddig meghatározott három kifejezésből (

m = 9 x

;

T N = 0, 801 - \frac{x}{3}

;

m \cdot T N = 0, 471

) a következő másodfokú egyenletre juthatunk:

3 x^{2} - 7, 21 + 0, 471 = 0

, melynek számunkra értelmes gyöke:

x = 0, 0672

. Így a kérdéses tömeg:

m = 9 x = 0, 605

kg, továbbá a dőlési szöget így határozhatjuk meg:

\begin{matrix} tg β = \frac{h}{x + \sqrt[]{3} h} = 0, 436, amiből β = 23, 6^{\circ} . \end{matrix}

2. A rendes munkavégző körfolyamat mennyiségei
2.1. A

μ (α)

forgatónyomaték függvény ábrázolása az

α

szög függvényében. Kezdetben (

α = 0

) nincs víz a kanálban. Ekkor az emelőrúdra ható forgatónyomaték:

\begin{matrix} M g \cdot T G = 30 \cdot 9, 81 \cdot 0, 0157 = 4, 62 Nm \approx 4, 6 Nm. \end{matrix}

Tekintsük ezt a forgatónyomatékot negatív előjelűnek, a negatív forgatónyomaték a rúd dőlésszögét csökkenteni igyekszik. Amikor lassan víz folyik a kanálba, az eredő forgatónyomaték növekedni kezd egészen addig, amíg kissé pozitívvé válik, és a mozsártörő emelkedni kezd. Ezt követően azzal a közelítéssel dolgozunk, hogy a kanálban lévő víz mennyisége nem változik.
Miközben a kanál lefelé billen, a benne lévő víz tömegközéppontja fokozatosan eltávolodik a forgástengelytől, így

μ

egészen addig növekszik, amíg a víz eléri a kanál peremét. Tehát a maximális forgatónyomaték az

α = α_{1} = 20, 6^{\circ}

-os dőlésszögnél jön létre. Az előző részben már megismert számoláshoz hasonlóan kiszámíthatjuk, hogy

μ_{{max}_{}^{}} \approx 2, 7

Nm.
A rúd további dőlése közben a víz elkezd kifolyni a kanálból, és

α = β

esetén

μ = 0

-vá válik. A tehetetlenség következtében

α

tovább növekszik, miközben

μ

csökken.

α = 30^{\circ}

esetén a kanál teljesen kiürül. Ebben a helyzetben a forgatónyomaték:

μ = - M g \cdot T G \cdot cos 30^{\circ} = - 4, 0

Nm. Ezután a tehetetlenség következtében a szög még tovább nő, egészen

α = α_{0}

értékig, amikor a forgatónyomaték:

μ = - M g \cdot T G \cdot cos α_{0} = - 4, 6 \cdot cos α_{0}

Nm. Végül a dőlésszög hirtelen nullára csökken (a mozsártörő lecsap), és a körfolyamat

μ = - 4, 6

Nm értékkel újra kezdődik.
A fentiek alapján felvázolhatjuk a

μ (α)

forgatónyomatékot az

α

szög függvényében (2. ábra):
2.2. A mozsártörő munkavégzésének grafikus értelmezése. A

μ (α)

forgatónyomaték által végzett

W_{teljes}

teljes munkavégzést a forgatónyomaték előjeles görbe alatti területeként számíthatjuk ki a teljes

O A B C D F O

körfolyamatra. A mozsártörőnek átadott

W_{ütés}

energiát az

α_{0}

-tól 0-ig tekintett görbe alatti terület mérőszámaként kaphatjuk meg (

E D F O E

), melynek nagysága:

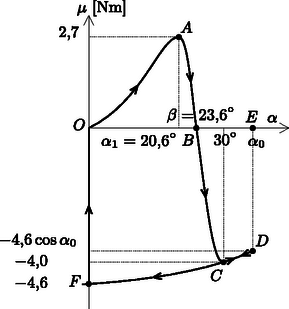\begin{matrix} M g \cdot T G \cdot sin α_{0} = 4, 6 J \cdot sin α_{0} . \end{matrix}

2. ábra

2.3. Az

α_{0}

szög és

W_{ütés}

becslése. Az

α_{0}

szög értékét abból becsülhetjük meg, hogy ebben a pozícióban az emelőrúd energiája nulla, vagyis az

O A B O

terület megegyezik a

B E D C B

terület nagyságával. Ha az

O A B O

területet háromszöggel, a

B E D C B

területet pedig trapézzal közelítjük, akkor az

α_{0}

szög értékére közelítőleg

35^{\circ}

-ot kapunk. Így a mozsártörő által végzett munka:

\begin{matrix} W_{ütés} = Mg \cdot T G \cdot sin α_{0} = 4, 6 J \cdot sin 35^{\circ} \approx 2, 6 J. \end{matrix}

3. A mozdulatlan állapot
3.1. Az emelőrúd mozgása az

α = β

egyensúlyi helyzet közelében.
3.1.1. Az

α = β

egyensúlyi helyzet közelében a forgatónyomaték nagyjából a 3. ábrán látható módon változik. A grafikon alapján megállapíthatjuk, hogy az egyensúlyi helyzet stabil.

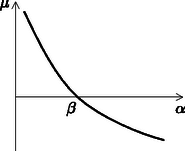3. ábra

3.1.2. Az

α

szögben megdőlt rúd esetén a kanálban lévő víz tömege:

\begin{matrix} m = \frac{ϱ b h \cdot P Q}{2}, ahol P Q = h (\frac{1}{tg α} - \frac{1}{tg 30^{\circ}}) . \end{matrix}

Miközben a rúd hajlásszöge

β

-ról (

β + Δ α

) értékre változik, a kanálban lévő víz tömegének megváltozása közelítőleg:

\begin{matrix} Δ m = - \frac{b h^{2} ϱ}{2 sin^{2} α} Δ α \approx - \frac{b h^{2} ϱ}{2 sin^{2} β} Δ α . \end{matrix}

A (

β + Δ α

) dőlésszögű rúdra ható

μ

forgatónyomaték megegyezik a

Δ m

tömegből származó nyomatékkal:

\begin{matrix} μ = Δ m g \cdot T N \cdot cos (β + Δ α) . \end{matrix}

T N

távolságot a rúd

β

szöghöz tartozó egyensúlyi állapotából határozhatjuk meg:

\begin{matrix} T N = \frac{M \cdot T G}{m} = \frac{30 \cdot 0, 0157}{0, 605} = 0, 779 m. \end{matrix}

Végül a forgatónyomatékra közelítőleg ezt a numerikus kifejezést kapjuk:

μ \approx - 47 \cdot Δ α

(Nm).
3.1.3. Alkalmazzuk a rúd mozgására a forgómozgás dinamikai alapegyenletét (

μ = I \frac{d^{2} α}{d t^{2}}

, ahol

α = β + Δ α

), melyben az

I

tehetetlenségi nyomaték nem csupán a rúdtól, hanem a kanálban lévő víz tömegétől is függ. Tegyük fel, hogy kicsiny

Δ α

szögek esetén a kanálban lévő víz tömege állandó (

\approx 0, 6

kg) és ezt a vízmennyiséget tekintsük tömegpontnak. A számítás a rendszer tehetetlenségi nyomatékára közelítőleg

I \approx 12, 4 kgm^{2}

-et ad. Így a mozgásegyenlet numerikus alakja (SI egységrendszerben):

\begin{matrix} - 47 \cdot Δ α = 12, 4 \frac{d^{2} Δ α}{d t^{2}}, \end{matrix}

ami egy harmonikus rezgőmozgás egyenlete. A mozgás rezgésideje:

\begin{matrix} τ = 2 π \sqrt[]{\frac{12, 4}{47}} \approx 3, 2 s. \end{matrix}

3.2. A vízhozam számítása kis amplitúdójú rezgés esetén. Az emelőrúd szögkitérésének időfüggését így írhatjuk fel az egyensúlyi helyzet körül:

\begin{matrix} Δ α = - Δ α_{0} sin (\frac{2 π t}{τ}), ahol Δ α_{0} = 1^{\circ} . \end{matrix}

Ilyenkor a rúd a

t = 0

kezdőpillanat után a kisebb szögkitérések felé indul el, és ott nagyobb vízmennyiségre van szükség a túlfolyás elérésére. Rövid

d t

idő alatt a rúd lehajlása

d α

szöggel változik meg:

\begin{matrix} d (Δ α) = d α = - Δ α_{0} \frac{2 π}{τ} cos (\frac{2 π t}{τ}) \cdot d t . \end{matrix}

A túlfolyáshoz ennyi idő alatt legalább a következő mennyiségű víznek kell a kanálba csorognia:

\begin{matrix} d m = - \frac{b h^{2} ϱ}{2 sin^{2} β} d α = \frac{2 π Δ α_{0} b h^{2} ϱ d t}{2 τ sin^{2} β} cos (\frac{2 π t}{τ}) . \end{matrix}

Ennek maximuma

t = 0

-nál van, vagyis a túlfolyás akkor lesz folyamatos, ha a vízhozamra (

d m = Φ d t

) teljesül, hogy

\begin{matrix} Φ \geq Φ_{1} = \frac{π b h^{2} ϱ}{τ sin β} Δ α_{0} = \frac{π b h^{2} ϱ}{τ sin β} \cdot \frac{2 π}{360} \approx 0, 23 kg/s, \end{matrix}

ahol a rezgés

1^{\circ}

-os szögamplitúdóját

\frac{2 π}{360}

radián alakban írtuk fel.
3.3. Mekkora minimális vízhozam esetén nem működik a mozsár? Ha a kanál eléri a

20, 6^{\circ}

-os dőlési szöget, miközben mindvégig túlcsordul, akkor benne 1 kg víz lesz, és a rezgési amplitúdója

23, 6^{\circ} - 20, 6^{\circ} = 3^{\circ}

-os lesz. Eltekintve a rendszer tehetetlenségi nyomatékának változásától (amit a növekvő vízmennyiség okoz), a háromszoros amplitúdó háromszoros vízhozamot is jelent:

Φ_{2} = 3 Φ_{1} \approx 0, 7

kg/s. Ennél nagyobb vízhozam esetén a rizshántoló mozsár nem tud működni.

2. feladat. Cserenkov-sugárzás és gyűrűs képalkotáson alapuló számláló

Mialatt a részecske

t

idő alatt a

C

pontból

s = v t = t β c

utat megtéve a

B

pontba ér, a

C

pontban kibocsátott fény egy

R = t \frac{c}{n}

sugarú gömböt ér el.
Így a hullámfront a

B

-ből a gömbhöz húzott érintő kúp, amely

\begin{matrix} φ = arcsin \frac{R}{s} = arcsin \frac{1}{β n} \end{matrix}

szöget zár be a részecske pályájával.

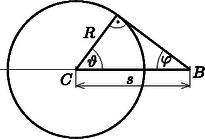4. ábra. A hullámfront szerkesztése

Adott irányból párhuzamosan érkező fénysugarakat a homorú gömbtükör a fókuszsíkba képzi. A kép pontos helyét a tükör

C

geometriai középpontján áthaladó sugármenet metszi ki, amely visszaverődés után szintén keresztülhalad

C

-n.
Az 5. ábrán felrajzoltuk az optikai tengelyhez képest

α

α + ϑ

és

α - ϑ

szögben haladó

C

-n átmenő fénysugarakat, melyek a fókuszsíkot az

O

M

és

N

pontban metszik. A tükör által alkotott kép (kis

α

ϑ

szögek esetén) egy

r = O M = O N = f ϑ

sugarú kör, melynek

O

középpontja

O F = f α

távolságra esik az

F

fókuszponttól.

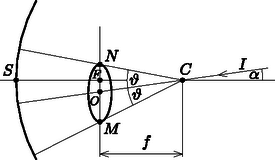5. ábra. A gyűrűs kép létrejötte

3.1. A

p = \frac{M v}{\sqrt[]{1 - β^{2}}}

(relativisztikus) impulzus képletéből az

M

nyugalmi tömeg ismeretében kifejezhető a részecskék

β = \frac{v}{c}

dimenziótlan sebessége:

\begin{matrix} β = {(1 + {(\frac{M c^{2}}{p c})}^{2})}^{- \frac{1}{2}} \approx 1 - δ, ahol δ = \frac{1}{2} {(\frac{M c^{2}}{p c})}^{2} . \end{matrix}

(1)

Az utolsó közelítés akkor érvényes, ha

δ ≪ 1

. Ez esetünkben jó közelítéssel fennáll mindhárom részecskére:

\begin{matrix} δ_{p} = 4, 42 \cdot 10^{- 3}, δ_{κ} = 1, 25 \cdot 10^{- 3}, δ_{π} = 9, 8 \cdot 10^{- 5} . \end{matrix}

(2)

A Cserenkov-effektus akkor lép fel, ha a részecske

v

sebessége nagyobb a közegbeli

\frac{c}{n}

fénysebességnél, ahol

n

a törésmutatót jelöli. Határesetben

v = \frac{c}{n_{{min}_{}^{}}}

, tehát a minimális törésmutató, amely mellett megfigyelhető a Cserenkov-effektus:

\begin{matrix} n_{min} = \frac{1}{β} = \sqrt[]{1 + {(\frac{M c^{2}}{p c})}^{2}} \approx 1 + δ . \end{matrix}

A törésmutató ismeretében a kritikus nyomás

P_{{min}_{}^{}} = \frac{n_{{min}_{}^{}} - 1}{a} = \frac{δ}{a}

. A számszerű eredmények:

\begin{matrix} P_{min, proton} = 16 atm, P_{min, kaon} = 4, 6 atm, P_{min, pion} = 0, 36 atm . \end{matrix}

3.2. A gyűrűk sugara

r = f ϑ

, ahol a sugárzási kúp

ϑ

félnyílásszögére a 4. ábra alapján a

cos ϑ = \frac{1}{n β}

egyenlőség teljesül. Most azt az

n_{\frac{1}{2}}

törésmutatót keressük, amely mellett

2 r_{κ} = r_{π}

, azaz

2 ϑ_{κ} = ϑ_{π}

. Ezek felhasználásával

\begin{matrix} \frac{1}{n_{\frac{1}{2}} β_{π}} = cos ϑ_{π} = cos (2 ϑ_{κ}) = 2 cos^{2} ϑ_{κ} - 1 = \frac{2}{n_{\frac{1}{2}}^{2} β_{κ}^{2}} - 1. \end{matrix}

Az egyenlőségsor első és utolsó eleme a

\begin{matrix} β_{π} β_{κ}^{2} n_{\frac{1}{2}}^{2} + β_{κ}^{2} n_{\frac{1}{2}} - 2 β_{π} = 0 \end{matrix}

(3)

másodfokú egyenletet adja a keresett

n_{\frac{1}{2}}

törésmutatóra, mely egyszerűen linearizálható, ha észrevesszük, hogy mind

n_{\frac{1}{2}}

, mind

β_{π}

és

β_{κ}

nagyon kicsit tér el

1

-től:

\begin{matrix} β_{π} \approx 1 - δ_{π}, β_{κ} \approx 1 - δ_{κ}, n_{\frac{1}{2}} = 1 + η . \end{matrix}

(4)

Ezeket a közelítéseket (3)-ba beírva, és csak az elsőrendű tagokat tartva meg, az adódik, hogy:

\begin{matrix} η = \frac{4 δ_{κ} - δ_{π}}{3} = 1, 634 \cdot 10^{- 3} és P_{\frac{1}{2}} = \frac{η}{a} = 6, 05 atm . \end{matrix}

Ezen a nyomáson a protonok nem keltenek Cserenkov-sugárzást. A törésmutató ismeretében meghatározható a kaonok és pionok által keltett sugárzási kúp félnyílásszöge:

\begin{matrix} ϑ_{κ} & = arccos (\frac{1}{n_{\frac{1}{2}} β_{κ}}) \approx \sqrt[]{2 (η - δ_{κ})} = 2, 77 \cdot 10^{- 2} rad = 1, 6^{\circ}, & (5) \\ ϑ_{π} & = 2 ϑ_{κ} = 5, 54 \cdot 10^{- 2} rad = 3, 2^{\circ} . \end{matrix}

(Ismert, hogy

x ≪ 1

esetén

cos x \approx 1 - \frac{x^{2}}{2}

. Innen

arccos (1 - y) \approx \sqrt[]{2 y}

, ahol

y = \frac{x^{2}}{2} ≪ 1

. A közelítésnél ezt az összefüggést, valamint a (4) egyenleteket használtuk fel.)
4.1. Az (1) és (5) egyenletek alapján a

ϑ

félnyílásszög a

p

impulzus függvényében

\begin{matrix} ϑ (p) \approx \sqrt[]{2 η - {(\frac{M c^{2}}{p c})}^{2}}, így \frac{d ϑ}{d p} \approx \frac{{(M c^{2})}^{2}}{ϑ \cdot {(p c)}^{3}} c . \end{matrix}

(6)

A számértékek behelyettesítése után azt kapjuk, hogy:

\begin{matrix} \frac{d ϑ_{κ}}{d p} = \frac{9, 03 \cdot 10^{- 3} \cdot c}{GeV} = \frac{0, 52^{\circ} \cdot c}{GeV}, \frac{d ϑ_{π}}{d p} = \frac{3, 54 \cdot 10^{- 4} \cdot c}{GeV} = \frac{0, 02^{\circ} \cdot c}{GeV} . \end{matrix}

(7)

(A részecskefizikában az impulzus megadására gyakran használják az

\frac{elektronvolt}{fénysebesség}

mértékegységet.)
4.2. A feltételekből az impulzus bizonytalansága:

\begin{matrix} Δ p < \frac{ϑ_{π} - ϑ_{κ}}{10 (ϑ'_{κ} + ϑ'_{π})} = 0, 3 \frac{GeV}{c} . \end{matrix}

5. Adott

n

törésmutatójú közegben Cserenkov-sugárzás a

v_{{min}_{}^{}} = \frac{c}{n}

sebesség fölött észlelhető. Ennél a sebességnél a mozgási energia:

\begin{matrix} T_{{min}_{}^{}} = \frac{M c^{2}}{\sqrt[]{1 - \frac{v_{{min}_{}^{}}^{2}}{c^{2}}}} - M c^{2} = M c^{2} (\frac{n}{\sqrt[]{n^{2} - 1}} - 1) = 0, 51 \cdot M c^{2} . \end{matrix}

α

-részecskékre, illetve elektronokra ezek az értékek

\begin{matrix} T_{α} = 0, 51 \cdot 3, 8 GeV = 1, 94 GeV, T_{β} = 0, 51 \cdot 0,51 MeV = 0, 26 MeV, \end{matrix}

ami azt jelenti, hogy elektronok hozták létre a Cserenkov által észlelt sugárzást.
6.1.

P

nyomáson

η = n - 1 = a P

, tehát a látható tartomány két végpontjához tartozó törésmutatók eltérése

Δ n = Δ η = 0, 02 \cdot a P = 3, 24 \cdot 10^{- 5}

. A keresett

Δ ϑ

szögeltérés a (6) egyenletben felírt

ϑ

szög

η

változó szerinti differenciálásával kapható meg:

\begin{matrix} Δ ϑ_{π} = \frac{d ϑ_{π} (η)}{d η} Δ η = \frac{Δ η}{ϑ_{π}} = 0, 033^{\circ} . \end{matrix}

6.2. Az előző pontban láttuk, hogy a diszperzió miatti kiszélesedés félértékszélessége

\frac{Δ ϑ_{π}}{2} = 0, 017^{\circ}

. A (7) egyenlet alapján az impulzus-inhomogenitás miatti kiszélesedés

\begin{matrix} \frac{0, 02^{\circ} \cdot c}{GeV} \cdot \frac{0, 3 GeV}{c} = 0, 006^{\circ}, \end{matrix}

ami háromszor kisebb a diszperzióhoz tartozó kiszélesedésnél. Kisebb hullámhosszon a törésmutató nagyobb, tehát a Cserenkov-kúp nyílásszöge szélesebb. Ez azt jelenti, hogy a gyűrű színe kívül kékes, középen fehér, belül pedig vöröses.

3. feladat. A levegő hőmérsékletének magasság szerinti változása, a légköri stabilitás és a légszennyeződés

1.1. A

z

magasságban levő,

ϱ (z)

sűrűségű,

A

területű,

d z

vastagságú levegőréteg

A ϱ (z) g d z

súlya megegyezik a levegőréteg alján és tetején mérhető nyomáskülönbségből származó

- A (p (z + d z) - p (z))

erővel. Felhasználva, hogy

ϱ = \frac{μ p}{R T_{0}}

, a nyomás magasságtól való függésére a

\begin{matrix} p' (z) = - \frac{μ g}{R T_{0}} p (z) \end{matrix}

differenciálegyenletet kapjuk, melynek megoldása

\begin{matrix} p (z) = p_{0} e^{- \frac{μ g}{R T_{0}} z} . \end{matrix}

1.2. Az előzőekhez hasonló érveléssel most a

p (z)

függvényre a

\begin{matrix} p' (z) = - \frac{μ g}{R (T (0) - Λ z)} p (z) \end{matrix}

(ún. szeparálható) differenciálegyenlet vezethető le, mely a feladatban közölt segítséggel megoldható:

\begin{matrix} \int \frac{d p}{p} = ln p + C_{1}; - \frac{μ g}{R} \int \frac{d z}{T (0) - Λ z} = \frac{μ g}{R Λ} ln (T (0) - Λ z) + C_{2}, \end{matrix}

ahonnan

\begin{matrix} p (z) = p_{0} {(1 - \frac{Λ z}{T (0)})}^{\frac{μ g}{R Λ}} . \end{matrix}

A sűrűség magasságtól való függése:

\begin{matrix} ϱ (z) = \frac{μ p (z)}{R T (z)} = \frac{μ p_{0}}{R T (0)} {(1 - \frac{Λ z}{T (0)})}^{\frac{μ g}{R Λ} - 1}, \end{matrix}

ami akkor monoton növekedő függvény, ha a kitevő negatív, azaz ha

\begin{matrix} Λ > \frac{μ g}{R} = 0, 034 \frac{K}{m} . \end{matrix}

Érdemes észrevenni, hogy kis magasságok esetén a nyomás magasságfüggése mind az 1. pontban vizsgált izoterm légkör esetén, mind pedig a most vizsgált lineáris hőmérséklet-eloszlás esetén

p (z) \approx p_{0} (1 - \frac{μ g z}{R T (0)})

alakú. Tehát a légkör hőmérsékletének magassággal való változása ,,első rendben'', kis magasságok esetén nem befolyásolja a nyomás magasságtól való függését.
2.1. A levegőcsomag állapotváltozása adiabatikus, tehát kielégíti a

\begin{matrix} T_{csomag} \cdot p^{\frac{1 - γ}{γ}} = állandó \end{matrix}

állapotegyenletet, ahol

T_{csomag} (z)

a levegőcsomag hőmérséklete,

p (z)

pedig a környezet és a levegőcsomag közös nyomása. Mindkét mennyiség függ a

z

magasságtól. Differenciáljuk az adiabatikus állapotegyenletet

z

szerint:

\begin{matrix} T_{csomag}' \cdot p^{\frac{1 - γ}{γ}} + T_{csomag} \cdot \frac{1 - γ}{γ} \cdot p^{\frac{1 - γ}{γ}} \cdot \frac{p'}{p} = 0. \end{matrix}

Az előző pontban láttuk, hogy

\frac{p'}{p} = - \frac{μ g}{R T}

, ezt felhasználva kapjuk, hogy:

\begin{matrix} T_{csomag}' = - G, ahol G = \frac{γ - 1}{γ} \frac{μ g}{R} \frac{T_{csomag}}{T} . \end{matrix}

(8)

2.2. Ha

T_{csomag} = T

, akkor

\begin{matrix} Γ = G |_{T_{csomag} = T} = \frac{γ - 1}{γ} \frac{μ g}{R} = \frac{μ g}{c_{p}} = 10^{- 2} \frac{K}{m}, \end{matrix}

és a hőmérséklet a

T (z) = T (0) - Γ z

módon függ a magasságtól. (Ezt a speciális esetet adiabatikus légkörnek hívják.)
2.3. Ha a külső hőmérséklet

T (z) = T (0) - Λ z

függvény szerint változik, akkor az (8) összefüggés szerint a

T_{csomag} (z)

függvény a következő differenciálegyenletet elégíti ki:

\begin{matrix} T_{csomag}' (z) = - \frac{Γ}{T - Λ z} T_{csomag} (z) . \end{matrix}

Az 1.2. pontban már megoldottunk egy hasonló differenciálegyenletet (

p (z)

-re, más konstanssal), így mostani egyenletünk megoldását a megfelelő változók átírásával azonnal megkaphatjuk:

\begin{matrix} T_{csomag} (z) = T_{csomag} (0) {(1 - \frac{Λ z}{T (0)})}^{\frac{Γ}{Λ}} \approx T_{csomag} (0) - Γ z . \end{matrix}

(9)

Az utolsó közelítés

| Λ z | ≪ T (0) \approx T_{csomag} (0)

esetén érvényes, amikor a hatványozás közelítésére használhatjuk az

{(1 + ε)}^{α} \approx 1 + α ε

formulát, amely

ε ≪ 1

esetén érvényes.
Érdemes észrevenni, hogy a kapott hőmérsékletfüggés megegyezik az adiabatikus légkör esetén kapottal. Ezen nem kell meglepődnünk, ha visszaemlékezünk az 1.2. pont végén kapott eredményünkre, mely szerint a külső nyomás (kis magasságok esetén, ,,első rendben'') érzéketlen a hőmérsélket magasságfüggésére, a külső hőmérséklet pedig (feltevéseink szerint) nem befolyásolja a levegőcsomag hőmérsékletét.
3.1. A levegőcsomag és a külső levegő nyomása egyensúlyban van, tehát csak hőmérsékletük eltérése okozhat sűrűségkülönbséget. Ha

z > 0

esetén a külső levegő

\begin{matrix} T (z) = T (0) - Λ z \end{matrix}

hőmérséklete kisebb, mint a levegőcsomag

\begin{matrix} T_{csomag} (z) = T (0) - Γ z \end{matrix}

hőmérséklete, azaz ha

Λ > Γ

, akkor a kissé felemelkedett levegőcsomag ritkább, mint környezete, tehát tovább emelkedik; a légkör instabil.

Λ = Γ

esetén a légkör semleges, míg

Λ < Γ

esetén stabil.
3.2. A levegőcsomag addig a

h

magasságig emelkedik, ahol hőmérséklete megegyezik a külső levegő hőmérsékletével, tehát, felhasználva a (9) egyenletet,

\begin{matrix} T (0) - Λ h = T_{csomag} (0) {(1 - \frac{Λ h}{T (0)})}^{\frac{Γ}{Λ}} . \end{matrix}

Innen a

h

magasságra azt kapjuk, hogy:

\begin{matrix} h = \frac{T (0)}{Λ} (1 - {(\frac{T (0)}{T_{csomag} (0)})}^{\frac{Λ}{Γ - Λ}}) \approx \frac{T_{csomag} (0) - T (0)}{Γ - Λ} . \end{matrix}

(10)

Az utolsó közelítés a

\begin{matrix} T_{csomag} (0) \approx T (0) és \frac{T_{csomag} (0) - T (0)}{T_{csomag} (0)} ≪ 1 \end{matrix}

feltételek mellett érvényes, és a

\begin{matrix} \frac{T (0)}{T_{csomag} (0)} = 1 - \frac{T_{csomag} (0) - T (0)}{T_{csomag} (0)} \end{matrix}

átírás után a hatványozás már megismert közelítésével kapható.
4.1. A táblázatból vett adatokat ábrázolva a következő grafikont kapjuk:

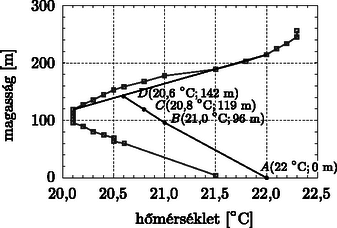6. ábra. A légkör hőmérséklete a magasság függvényében

Ennek megfelelően a légkör három rétegre osztható, a középső réteg izoterm, míg a másik kettőben közel lineárisan változik a hőmérséklet:

\begin{matrix} 1. réteg & 0 m < z < 96 m & Λ_{1} = \frac{21, 5 K - 20, 1 K}{91 m} = 15, 4 \cdot 10^{- 3} \frac{K}{m} \\ 2. réteg & 96 m < z < 119 m & Λ_{2} = 0 \frac{K}{m}, izoterm szakasz \\ 3. réteg & 119 m < z < 215 m & Λ_{3} = \frac{20, 1 K - 22 K}{215 m - 119 m} = - 0, 02 \frac{K}{m} \end{matrix}

Látható, hogy a (9) egyenlet közelítésénél használt feltételek teljesülnek, így a felemelkedő, és adiabatikusan táguló levegőcsomag hőmérséklete a külső hőmérséklettől lényegében teljesen függetlenül a

Γ = 10^{- 2} \frac{K}{m}

együttható szerint lineárisan csökken. Így

\begin{matrix} T_{csomag} (96 m) & = 22^{\circ} C - 0, 96^{\circ} C \approx 21, 0^{\circ} C és \\ T_{csomag} (119 m) & = 22^{\circ} C - 1, 19^{\circ} C \approx 20, 8^{\circ} C . \end{matrix}

4.2. Látható, hogy 119 m magasan a levegőcsomag hőmérséklete még mindig

0, 7^{\circ}

C-kal magasabb, mint környezetéé. Alkalmazva a (10) egyenlet közelítő formuláját, azt kapjuk, hogy a levegőcsomag még további

\frac{0, 7}{0, 01 + 0, 02} m = 23 m

-t emelkedik, mire környezetével hőmérsékleti egyensúlyba kerül. Tehát a keverési magasság

\begin{matrix} H = 119 m + 23 m = 142 m, \end{matrix}

és itt a hőmérséklet

T_{csomag} (H) \approx 20, 6^{\circ}

C.
5.1. Az

L \times W \times H

méretű téglatestben levő teljes szén-monoxid mennyiség két tényező miatt változik: egyrészt a motorok által kibocsátott mennyiséggel nő, másrészt a szél által kifújt mennyiséggel csökken. Tehát

\begin{matrix} L W H C' (t) = M - u L H C (t) . \end{matrix}

5.2. A fenti lineáris elsőrendű differenciálegyenletnek a

C (0) = 0

kezdőfeltételt kielégítő megoldása:

\begin{matrix} C (t) = \frac{M}{L H u} (1 - e^{- \frac{u}{W} t}) . \end{matrix}

5.3. A fenti egyenletbe behelyettesítve a megadott adatokat, azt kapjuk, hogy a 8 órakor mérhető szén-monoxid koncentráció

C (3600 s) = 2, 3 \frac{mg}{m^{3}}