Cím:	A 2007‐2008. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2008/november, 451 - 457. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. KEZDŐK   I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. Az ábrán látható alakzatot öt egybevágó egyenlőszárú háromszögből és öt egybevágó négyzetből állítottuk össze. A tíz alakzat közül bármely kettőnek legfeljebb a határpontjai között lehetnek azonosak. Határozza meg az egyenlő szárú háromszögek belső szögeinek nagyságát!     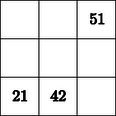2. Egy bűvös négyzetben minden sorban, oszlopban és átlóban a számok összege ugyanannyi. Határozza meg az alábbi bűvös négyzetből hiányzó hat számot!     3. Egy országban 9 nagyváros van. Ezek közül mindegyikből pontosan 4 nagyvárosba van oda és vissza is repülőjárat. Bizonyítsa be, hogy bármely nagyvárosból legfeljebb egy átszállással bármely nagyvárosba el lehet jutni!   4. A $\mathrm{3,6,12,5,10,}\text{...}$ számsorozat elemeit a második elemtől kezdve úgy kaptuk, hogy az előző elem egyes helyiértéken álló számjegyének kétszeresét hozzáadtuk ahhoz a számhoz, amit ennek a számjegynek az elhagyásával kaptunk. Mi lesz a sorozat 2007-dik eleme?   Második forduló   1. 23 diák írt meg egy dolgozatot, az átlag (két tizedes jegyre kerekítve) 2,74 lett. Lehet-e kevesebb, mint két elégtelen, ha tudjuk, hogy nyolc jeles volt?   2. Egy derékszögű háromszög átfogója 13 cm és a befogóinak összege 17 cm. A háromszög mindhárom oldalára kifelé négyzeteket rajzolunk. Így a háromszög csúcsain kívül hat pontot kapunk. Mekkora az ezek által meghatározott hatszög területe?   3. Egy 8 fős társaság olyan kártyajátékot játszik, amelyet 4-en kell az óramutató járásával ellentétes irányba játszani. Mindig két négyes csoportban játszanak. Elhatározzák, hogy az összes lehetséges összetételben fognak játszani. (Két összetétel akkor különböző, ha a két 4-es csoport közül legalább az egyikben van olyan játékos, aki után másik játékos következik az egyik összetételben, mint a másikban.) Kb. hány év alatt tudják teljesíteni elhatározásukat, ha hetente egy összetételben játszanak?   4. Egy kékre befestett téglatest élei cm-ben mérve természetes számok és az egyik él hossza 7 cm. A téglatestet a lapjaival párhuzamos síkokkal 1 cm élű kis kockákra szétvágva a kék lappal nem rendelkező kis kockák száma feleakkora, mint az összes kis kockák száma. Mennyi az ilyen tulajdonságú téglatestek közül a legkisebb térfogatúnak a térfogata?   5. Az $a$, $b$, $c$ és $d$ valós számokra teljesül, hogy $a^2+b^2=c^2+d^2$ és $ac+bd=0$. Mennyi lehet az $ab+cd$ értéke?   Harmadik (döntő) forduló   1. Egy négyzet egyik csúcsából úgy húzunk két félegyenest, hogy azok a négyzetet három síkidomra bontsák fel. Mekkora ennek a három síkidomnak a területe, ha kerületük ugyanakkora és a négyzet oldalainak hossza $a$?   2. Egy matematika órán a tanár felírt egy pozitív egész számot a táblára. Az egyik diák így szólt: a szám osztható 31-gyel. A második diák azt mondta, hogy a szám osztható 30-cal, a harmadik pedig azt, hogy a szám osztható 29-cel. Ezt a felsorolást addig folytatták a diákok, amíg a harmincadik is megszólalt: a szám osztható 2-vel. A tanár ezek után közölte, hogy a fenti harminc állítás közül csak kettő hamis és a két hamis állítás közvetlenül egymás után hangzott el. Melyik volt a két hamis állítás?   3. Adott egy $2008\times 2008$-as négyzetrács. Behúzunk egy a négyzetrácsot metsző egyenest. Legfeljebb hány mező belsején haladhat át ez az egyenes?   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló   Megegyezik az I. kategória első fordulós feladatsorával.   Második forduló   Megegyezik az I. kategória második fordulós feladatsorával.   Harmadik (döntő) forduló   1. Egy matematika órán a tanár felírt egy pozitív egész számot a táblára. Az egyik diák így szólt: a szám osztható 31-gyel. A második diák azt mondta, hogy a szám osztható 30-cal, a harmadik pedig azt, hogy a szám osztható 29-cel. Ezt a felsorolást addig folytatták a diákok, amíg a harmincadik is megszólalt: a szám osztható 2-vel. A tanár ezek után közölte, hogy a fenti harminc állítás közül csak kettő hamis és a két hamis állítás közvetlenül egymás után hangzott el. Melyik volt a két hamis állítás?   2. Néhány egész szám összege 0. Bizonyítsa be, hogy a számok ötödik hatványainak összege osztható 15-tel!   3. Az $ABC$ háromszögben $AB=AC$. Legyen a $B$ pontnak az $AC$ oldalra vett merőleges vetülete $T$! Mekkorák a háromszög szögei, ha $AC-2\cdot CT=BC$?   III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló   Megegyezik az I. kategória második fordulós feladatsorával.   Második (döntő) forduló   1. Adott kerületű háromszögek közül vizsgáljuk azt, amelyiknél a háromszög beírt körön kívüli részének területe maximális. Mekkora a beírt kör sugara?   2. Legyenek $a$ és $b$ páratlan pozitív egész számok, melyek relatív prímek, azaz $\left(a\mathrm{,}b\right)=1$. Bizonyítsa be, hogy az $A=a^{2^{2008}}-b^{2^{2008}}$ számnak legalább 2008 db különböző prímosztója van.   3. Nevezzük egy konvex $n$-szög három szomszédos csúcsa által meghatározott ($n$ db) háromszöget sarokháromszögnek. Adjunk példát olyan konvex 2008-szögre, melyben a csúcsok által meghatározott összes háromszög közül a 2008 db legkisebb területű háromszögből legfeljebb 63 db sarokháromszög van.   HALADÓK   I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. Párba lehet-e állítani a szabályos tízszög csúcsait úgy, hogy a párba állított pontok által meghatározott öt távolság mind különböző?   2. Tizenhat különböző magas gyereket négy sorba és négy oszlopba állítunk. Minden sorban a legalacsonyabb felteszi a bal kezét. Közöttük Jakab a legmagasabb. Minden oszlopban a legmagasabb felteszi a jobb kezét. Közöttük Boldizsár a legalacsonyabb. Ki a magasabb, Jakab vagy Boldizsár?     3. Az $O_1$ középpontú, $R$ sugarú $k_1$ kört kívülről érinti az $O_2$ középpontú, $2R$ sugarú $k_2$ kör és mindkettőt ugyancsak kívülről érinti az $O_3$ középpontú, $3R$ sugarú $k_3$ kör. Bizonyítsa be, hogy az $O_1{O}_2{O}_3$ háromszög beírt köre egybevágó a $k_1$ körrel!   4. Határozzuk meg azt a legnagyobb pozitív egész számot, amely bármely pozitív egész $n$-re osztója az alábbi kifejezésnek: $\begin{array}{c}{\displaystyle n^4{\left(n-1\right)}^3{\left(n-2\right)}^2\left(n-3\right)\mathrm{.}}\end{array}$   5. Az $x$ számról tudjuk, hogy $x+\frac{1}{x}=4$. Számítsa ki $\frac{x^2}{x^4+1}+\frac{1}{x^2}+x^2$ értékét! (Olyan formában megadott érték számít teljes értékű megoldásnak, amiből kiderül, hogy a szám racionális-e vagy nem, és az is, hogy melyik a hozzá legközelebbi egész.)   Második forduló   1. Határozza meg az összes olyan $x$ egész számot, amelyre az $x^2+19x+95$ kifejezés négyzetszámot ad!   2. Az $f\left(x\right)=a{x}^2+bx+c$ másodfokú függvényre $f\left(a\right)=b$, $f\left(b\right)=c$ és $f\left(c\right)=a$ teljesül. Mi lehet ekkor $a^3+b^2+c$ értéke?   3. Keresse meg az $ABC$ háromszög síkjában az összes olyan $P$ pontot, amelyre az $ABP$, $BCP$ és $CAP$ háromszögek területe egyenlő!   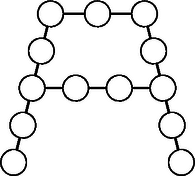4. A 34 éves ADONISZ áruházlánc születésnapi ajándékként vásárláskor vevőinek minden 100 forintos tétel után egy olyan sorsjegyet ad, amelyen az áruház emblémája látható. Ha a vevő be tudja írni a körökbe a számokat 1-től 13-ig úgy, hogy minden szám pontosan egyszer szerepeljen, és a beírt számok összege minden egyenes vonal mentén 34 legyen, akkor a sorsjegy részt vesz a sorsoláson. Egy vevő több sorsjegyet is leadhat, de két sorsjegyet nem tölthet ki azonos módon. Legalább hány forintért vásárolt az a vevő, aki a legnagyobb esélyt akarja biztosítani magának, azaz az összes lehetséges módon kitöltötte a sorsjegyeket?     Harmadik (döntő) forduló   1. 2008 darab pozitív egész szám szorzata egyenlő az összegükkel. Közülük a legkisebb $k$-szor fordul elő az előállításban. Igazoljuk, hogy $1996<k\le 2006$.   2. Egy konvex négyszög középvonalai a szemben levő oldalak felezőpontjait összekötő szakaszok. Az $ABCD$ konvex négyszögről tudjuk, hogy területe megegyezik középvonalai hosszának szorzatával. Bizonyítsuk be, hogy ekkor $AC=BD$, vagyis, hogy a négyszög átlói egyforma hosszúak! Van-e a téglalapokon kívül más olyan négyszög, ami ilyen tulajdonságú, azaz olyan, hogy területe megegyezik középvonalai hosszának szorzatával?   3. Egy szabályos $n$-szög csúcsaihoz tetszőleges módon a ,,$-$'' vagy a ,,$+$'' előjelet rendeljük hozzá. Egy lépésben bármely három szomszédos csúcs előjelét megváltoztatjuk. $a)$ Igazoljuk, hogy $n=2008$ esetén bármely kezdőhelyzetből indulva elérhető, hogy mindegyik csúcs előjele ,,$+$'' legyen. $b)$ Bizonyítsuk be, hogy $n=2007$ esetén van olyan kiindulási helyzet, amelyből az adott lépés többszöri alkalmazásával soha nem érhető el, hogy mindegyik csúcs előjele ,,$+$'' legyen.   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló   1. Bizonyítsuk be, hogy $n!+2007$ egyetlen $n$ pozitív egész szám esetén sem prímszám, sem pedig négyzetszám. ($n!$ az $1\cdot 2\cdot 3\cdot \text{...}\cdot n$ szorzatot jelenti.)   2. Adott a síkon egy egységnyi oldalú szabályos hatszög. Szerkesszünk csak vonalzó felhasználásával $\sqrt[]{7}$ hosszúságú szakaszt!   3. A minden valós számra értelmezett másodfokú $f\left(x\right)$ függvényre $\begin{array}{c}{\displaystyle f\left(x+2\right)+3f\left(-x\right)=2x^2}\end{array}$ teljesül. Határozzuk meg az $f\left(x\right)$ függvény értékkészletét!   4. Az ábrán látható módon helyezzük el az $ABCDEF$ szabályos egységoldalú hatszögben a $PQBA$ egységoldalú négyzetet. Gördítsük körbe a hatszög belső felületén a négyzetet a következő módon: először az óramutató járásával megegyezően forgassuk a négyzetet a $B$ körül mindaddig, amíg a négyzet $Q$ csúcsa a hatszög $C$ csúcsához ér. Ezután $C$ körül forgassuk az óramutató járásával megegyezően a négyzetet, míg $P$ egybeesik $D$-vel. Majd $D$ körül forgassuk az óramutató járásával megegyezően a négyzetet, amíg a négyzet csúcsa a hatszög $E$ csúcsához ér.     Folytassuk tovább ezt az eljárást mindaddig, amíg a négyzet a hatodik forgatás után vissza nem ér az $AB$ oldalhoz. Milyen hosszú utat jár be ezalatt $P$?   5. Bizonyítsuk be, hogy egy kocka a lapjaival párhuzamos síkdarabokkal feldarabolható 2007 darab nem feltétlenül egybevágó kisebb méretű kockára.   Második forduló   1. Hány olyan pozitív egész számokból álló $\left(x;y\right)$ számpár van, amelyre $\frac{1}{x}-\frac{1}{y}=\frac{1}{2008}$ teljesül?   2. Ha $\frac{1}{\sqrt[]{x}}+\frac{1}{\sqrt[3]{x}}=\frac{1}{\sqrt[6]{x}}$, akkor igazoljuk, hogy $x+\frac{1}{x}$ egész szám.   3. Az $ABC$ háromszög $A$ csúcsból húzott belső szögfelezője a $BC$ oldalt $P$-ben metszi. A $C$ csúcsból induló $CT$ magasság az $E$ pontban felezi az $AP$ szakaszt. Bizonyítsuk be, hogy ha a $PCE$ háromszög területe kétszerese az $ATE$ háromszög területének, akkor az $ABC$ háromszög derékszögű.   4. A 34 éves ADONISZ áruházlánc születésnapi ajándékként vásárláskor vevőinek minden 100 forintos tétel után egy olyan sorsjegyet ad, amelyen az áruház emblémája látható. Ha a vevő be tudja írni a körökbe a számokat 1-től 13-ig úgy, hogy minden szám pontosan egyszer szerepeljen, és a beírt számok összege minden egyenes vonal mentén 34 legyen, akkor a sorsjegy részt vesz a sorsoláson. Egy vevő több sorsjegyet is leadhat, de két sorsjegyet nem tölthet ki azonos módon. Legalább hány forintért vásárolt az a vevő, aki a legnagyobb esélyt akarja biztosítani magának, azaz az összes lehetséges módon kitöltötte a sorsjegyeket?     Harmadik (döntő) forduló   1. Induljunk ki egy tetszőleges 2008 jegyű számból, és képezzünk az alábbi szabály szerint egy egészekből álló számsorozatot. A sorozat következő tagját az előzőből úgy kapjuk, hogy annak számjegyei összegét $x$-szel jelölve kiszámoljuk az $\frac{x\left(x-1\right)}{2}$ kifejezés értékét. Bizonyítsuk be, hogy akármilyen 2008-jegyű egész számból indulunk is ki, a kapott sorozat 2007. és 2008. tagja egyenlő.   2. Egy négyzet alakú asztal négy lába 1 méter hosszú. Mindegyik lábból levághatunk egy egész deciméternyi darabot. Az is lehet, hogy semmit nem vágunk, és az egész lábat is levághatjuk. A vágások hosszát egy rendezett $\left(v_1\mathrm{,}{v}_2\mathrm{,}{v}_3\mathrm{,}{v}_4\right)$ négyessel írhatjuk le, a lábakat megkülönböztetjük. Hányféle $\left(v_1\mathrm{,}{v}_2\mathrm{,}{v}_3\mathrm{,}{v}_4\right)$ vágásra teljesül, hogy a megmaradt asztal nem billeg? Az asztal akkor nem billeg, ha elhelyezhető a vízszintes talajon úgy, hogy mind a négy láb leér a földre.   3. Az $n$ természetes számot bájosnak nevezzük, ha összetett, és egynél nagyobb osztói felírhatók egy kör kerületére úgy, hogy a szomszédos számok nem relatív prímek. Hány bájos szám van az $\left\{\mathrm{1,2,3,}\text{...}\mathrm{,100}\right\}$ halmazban?   III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló   1. Egy sorozatot a következő módon adunk meg: $a_0=9$, és $a_{k+1}=3a_k^4+4a_k^3$, ha $k\ge 0$. Bizonyítsuk be, hogy $a_{10}$ legalább 1000 darab kilences számjegyre végződik!   2. Bizonyítsuk be, hogy az $1+2+\text{...}+n$ összeg semmilyen természetes szám esetén sem végződhet sem 12-re, sem 13-ra, sem 14-re!   3. Legyen $A_n=\left\{1;2;3;\text{...};n\right\}$, ahol $n>3$. Tekintsük az $A_n$ halmaz olyan háromelemű részhalmazait, amelyek elemei egy háromszög oldalhosszai lehetnek. Az ilyen tulajdonságú háromelemű részhalmazok számát $f\left(n\right)$-nel jelöljük. Mekkora $n$ értéke, ha $\begin{array}{c}{\displaystyle f\left(n+1\right)-f\left(n\right)=100?}\end{array}$   4. Az $A$, $B$, $C$, $D$ és $E$ egy kör kerületének olyan pontjai, amelyekre igaz, hogy $\begin{array}{c}{\displaystyle ABC\sphericalangle =CDE\sphericalangle =BCD\sphericalangle ={45}^{\circ }\mathrm{.}}\end{array}$ Bizonyítsuk be, hogy $\begin{array}{c}{\displaystyle A{B}^2+C{D}^2=B{C}^2+D{E}^2\mathrm{.}}\end{array}$     5. Bergengóciában új számrendszert vezetnek be. A pozitív egészeket $\begin{array}{c}{\displaystyle n=\overline{a_k\text{...}{a}_1{a}_0}=a_k\cdot 2^k+\text{...}+a_1\cdot 2+a_0}\end{array}$ alakban írják fel, ahol $a_i\in \left\{\mathrm{0,1,2}\right\}$. Ebben a rendszerben egy szám többféle módon is felírható. Például: $\begin{array}{c}{\displaystyle 18=\overline{2010}=2\cdot 8+1\cdot 2=\overline{10010}=1\cdot 16+1\cdot 2.}\end{array}$ Hányféle különböző felírása van a 2008-nak ebben az új számrendszerben?   Második (döntő) forduló   1. A $v_1$ számnégyes az $a_1$, $b_1$, $c_1$, $d_1$ pozitív egész számokból áll, ahol $v_1=\left(a_1;b_1;c_1;d_1\right)$, és $a_1$, $b_1$, $c_1$, $d_1$ egyike sem nagyobb 2008-nál. A $v_2$ rendezett számnégyes: $v_2=\left(a_2;b_2;c_2;d_2\right)$, ahol $a_2=|a_1-b_1|$, $b_2=|b_1-c_1|$, $c_2=|c_1-d_1|$, $d_2=|d_1-a_1|$. Teljesen hasonló módon a $v_{n+1}$ számnégyes képzési szabálya $v_{n+1}=\left(a_{n+1};b_{n+1};c_{n+1};d_{n+1}\right)$ esetén $a_{n+1}=|a_n-b_n|$, $b_{n+1}=|b_n-c_n|$, $c_{n+1}=|c_n-d_n|$, $d_{n+1}=|d_n-a_n|$. Bizonyítsuk be, hogy $v_{2008}=\left(0;0;0;0\right)$!   2. Határozzuk meg az összes pozitív egészekből álló $\left(x;y\right)$ számpárt, ami kielégíti az alábbi egyenletet: $\begin{array}{c}{\displaystyle y^2\left(x-1\right)=x^5-1.}\end{array}$   3. Az $ABC$ szabályos háromszög $AB$ oldalának a felezőpontjától különböző tetszőleges belső pontja $P$. Az $APC$ háromszög beírt köre $k_1$, a $BPC$ háromszög beírt köre $k_2$. A $k_1$ és $k_2$ körnek a $PC$ egyenestől különböző közös belső érintője a $Q$ pontban metszi az $AB$ szakaszt. Bizonyítsuk be, hogy a $Q$ pont helyzete független $P$ megválasztásától!