Kezdőlap


Cím:	A 39. Nemzetközi Fizikai Diákolimpia elméleti feladatai
Füzet:	2008/október, 424 - 433. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

¹
1. feladat. ,,Vízzel hajtott rizshántoló mozsár''

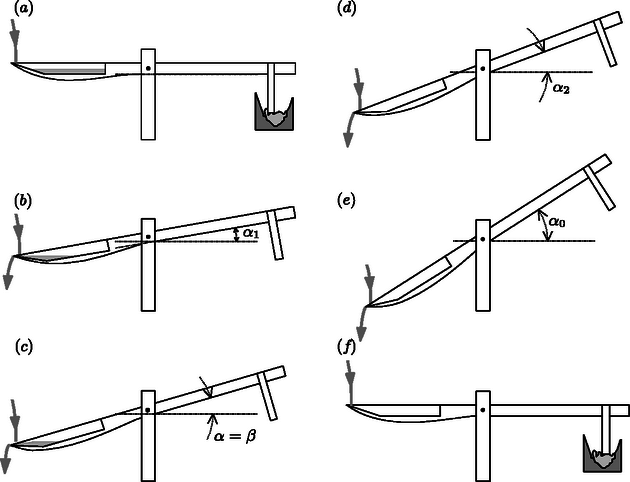
Bevezetés. Vietnamban a legtöbb embernek a rizs a fő tápláléka. A fehér rizst úgy készítik a hántolatlan rizsből, hogy hántolják, vagyis egy réteget eltávolítanak a rizsszemek felületéről. Észak-Vietnam hegyvidékei vízben gazdagok, és az ott élő emberek vízzel hajtott rizshántoló mozsarakat használnak ehhez a munkához. Az 1. ábra egy ilyen mozsarat mutat, a 2. ábrán pedig az látható, hogyan működik.

1. ábra. Vízzel hajtott rizshántoló mozsár

Tervezés. Az 1. ábrán látható rizs-hántoló mozsár a következő részekből áll:
A mozsár, lényegében egy fa tartály a rizs számára.
Az emelő, ami egy fatörzs, egyik vége vastagabb, a másik vékonyabb. Az emelő vízszintes tengely körül tud elfordulni. A mozsártörőt merőlegesen rögzítik az emelő vékonyabb végére. A mozsártörőt olyan hosszúra készítik, hogy akkor érje el a mozsárban a rizst, amikor az emelő vízszintes. Az emelő vastagabb végét úgy alakítják ki, hogy egy üreget vágnak ki belőle, így egy kanalat vájnak ki a farúd végén. A kanál alakja nagyon fontos a mozsár működésében.
A működés szakaszai. A mozsár működése kétféle lehet.
Rendes, munkavégző körfolyamat. Ilyenkor a mozsár a 2. ábrán bemutatott működési ciklust végzi.
A rizshántoló funkció abból a munkából származik, amit a mozsártörő a rizsnek közvetít a 2. ábra

(f)

lépésében. Ha valamilyen okból a mozsártörő nem éri el a rizsszemeket, azt mondjuk, hogy a mozsár nem végez munkát.

2. ábra

Rendellenes, mozdulatlan állapot. A működési ciklus

(c)

lépésében (2. ábra), amikor az

α

dőlési szög növekszik, a kanálban lévő víz mennyisége csökken. Egy bizonyos időpillanatban a víz mennyisége éppen elegendő ahhoz, hogy egyensúlyban tartsa a szerkezet rúdját. Jelöljük a dőlési szöget ebben a pillanatban

β

-val. Ha az emelőrudat a

β

szögben tartjuk, és a kezdeti szögsebesség nulla, akkor az emelőrúd örökre ebben a helyzetben marad. Ez a mozdulatlan állapot felemelt emelőrúddal. Ennek a helyzetnek a stabilitása a kanálba folyó

Φ

vízmennyiségtől (vízhozamtól) függ. Ha

Φ

meghalad egy bizonyos

Φ_{2}

értéket, akkor a mozdulatlan állapot stabil, és a mozsár nem kerülhet a munkavégző funkcióba. Más szavakkal:

Φ_{2}

-nél nagyobb vízhozam esetén a mozsár nem működik.
A rizshántoló mozsár működési ciklusa:

(a)

Kezdetben nincs víz a kanálban, a mozsártörő a mozsárban nyugszik. Lassan csordogálva víz folyik a kanálba, eközben az emelő rúdja mégis vízszintes helyzetű marad.

(b)

Egy bizonyos pillanatban a víz mennyisége eléri azt a határt, ami az emelőrúd felemeléséhez kell. A megdőlés hatására a víz megindul a kanál távolabbi oldala felé, ezzel még gyorsabban dönti az emelőrudat. A víz az

α = α_{1}

szöghelyzet elérésekor kezd kifolyni.

(c)

Amint az

α

szög növekszik, a víz tovább folyik ki. Egy bizonyos

α = β

dőlési szögnél a teljes forgatónyomaték nulla.

(d)

α

folyamatosan növekszik, a víz kifolyása addig folytatódik, amíg a kanál teljesen kiürül.

(e)

α

továbbra is növekszik a rendszer tehetetlensége miatt. A kanál alakja miatt hiába folyik víz a kanálba, az azonnal kifolyik onnan. Az emelőrúd tehetetlenségi mozgása addig folytatódik, amíg

α

eléri a maximális

α_{0}

értékét.

(f)

Mivel nincs víz a kanálban, az emelőrúd súlya visszahúzza a rendszert az eredeti vízszintes helyzetbe. A mozsártörő belecsapódik a (rizst tartalmazó) mozsárba, és ezután egy új ciklus kezdődik el.
A probléma. Az általunk vizsgált vízzel hajtott rizshántoló mozsár (3. ábra) paraméterei a következők: Az emelőrúd tömege (a mozsártörővel együtt, ha a kanálban nincs
víz):

M = 30

kg. Az emelőrúd tömegközéppontja

G

. Az emelőrúd a

T

tengely körül forog (melynek vetülete az ábrán a

T

pont). Az emelőnek a

T

tengelyre vonatkoztatott tehetetlenségi nyomatéka:

I = 12 kg\cdotm^{2}

. Amennyiben a kanálban víz van, ennek a víznek a tömegét jelölje

m

, tömegközéppontja pedig legyen

N

. Az emelőrúd vízszinteshez viszonyított dőlésszöge

α

.
A berendezés legfontosabb geometriai adatait a 3. ábra mutatja.

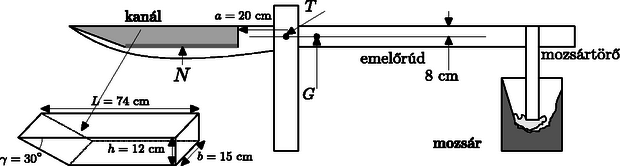3. ábra. A rizshántoló mozsár tervrajza és méretezése

Hanyagoljuk el a tengely körüli forgáskor fellépő súrlódást, valamint a kanálba eső víz által kifejtett erőt. Továbbá közelítésként tekintsük a kanálban levő víz felszínét mindig vízszintesnek.

1. A mozsár felépítése.
Kezdetben a kanál üres, és az emelőrúd vízszintes. Ezután fokozatosan egyre több víz folyik a kanálba, mígnem az emelőrúd elkezd forogni. Ebben a pillanatban a kanálban levő víz mennyisége:

m = 1, 0

kg.
1.1. Határozd meg az emelőrúd

G

tömegközéppontjának a

T

forgástengelytől mért távolságát! Ha a kanál üres,

G T

vízszintes.
1.2. Amikor az emelőrúd eléri a vízszinteshez viszonyított

α_{1}

szögű helyzetet, a víz elkezd kifolyni a kanálból, míg az emelőrúd

α_{2}

szögű helyzeténél a kanál teljesen kiürül. Határozd meg az

α_{1}

és az

α_{2}

szöget!
1.3. Legyen

μ (α)

a (

T

tengelyre vonatkoztatott) teljes forgatónyomaték, amely az emelőrúd, valamint a kanálban levő víz súlyából származik. A

μ (α)

forgatónyomaték

α = β

esetén zérussá válik. Határozd meg a

β

szöget, valamint ebben a helyzetben a kanálban levő víz

m_{1}

tömegét!

2. Rendes munkavégző körfolyamat.
Tegyük föl, hogy a kanálba csorgó víz

Φ

hozama időben állandó, és kicsiny. Így az emelőrúd mozgása közben a kanálba folyó víz mennyisége elhanyagolható. Ebben a feladatban hanyagoljuk el a munkavégzési ciklus során a szerkezet tehetetlenségi nyomatékának változását.
2.1. Ábrázold egy teljes munkavégzési ciklusra a

μ (α)

függvényt, azaz rajzold fel a

μ

forgatónyomatékot az

α

szög függvényében! Add meg számszerűen

μ (α)

értékét az

α_{1}

α_{2}

és

α = 0

szög esetén!
2.2. A 2.1. pontban kapott grafikon elemzésével add meg a

μ (α)

forgatónyomaték által végzett

W_{teljes}

teljes munka, valamint a mozsártörő becsapódásakor a rizsnek átadott

W_{ütés}

energia geometriai értelmezését!
2.3. A

μ

forgatónyomatékot

α

függvényében ábrázoló grafikon alapján becsüld meg az

α_{0}

szög és a

W_{ütés}

becsapódási energia értékét! (A kanálba be- és kifolyó víz kinetikus energiája elhanyagolhatónak tekinthető.) A számolás egyszerűsítése érdekében, ha szükséges, görbe vonalakat törtvonalakkal helyettesíthetsz a grafikonon.

3. A mozdulatlan állapot.
Folyjon víz a kanálba állandó

Φ

vízhozammal, azonban most nem hanyagolhatjuk el a kanálba befolyó víz mennyiségét az emelőrúd mozgása közben.
3.1. Tegyük fel, hogy a kanálból mindig túlfolyik a víz.
3.1.1. Vázold fel egy grafikonon a

μ

forgatónyomatékot az

α

szög függvényében az

α = β

eset közelében. Állapítsd meg az

α = β

egyensúlyi helyzet stabilitását!
3.1.2. Határozd meg a forgatónyomaték

μ (α)

matematikai kifejezését mint

Δ α

függvényét, ahol

α = β + Δ α

, és

Δ α

kicsi.
3.1.3. Írd fel az emelőrúd mozgásegyenletét, ha nulla kezdősebességgel indul el

α = β + Δ α

helyzetből (

Δ α

kicsi). Mutasd meg, hogy a mozgás nagy pontossággal harmonikus rezgés. Számítsd ki a

τ

periódusidőt!
3.2. Adott

Φ

esetén a kanál minden időpillanatban túlfolyik, de csak akkor, ha az emelőrúd mozgása elegendően lassú. A harmonikus rezgőmozgás amplitúdójára létezik egy felső korlát, ami

Φ

-től függ. Határozd meg

Φ

-nek a minimális

Φ_{1}

értékét (kg/s egységben) akkor, ha az emelőrúd

1^{\circ}

-os amplitúdóval harmonikus rezgőmozgást végez.
3.3. Tegyük fel, hogy

Φ

elegendően nagy ahhoz, hogy az emelőrúd szabad mozgása közben, amikor a dőlési szög

α_{2}

-ről

α_{1}

-re csökken, a kanálban lévő víz mindig túlfolyjon. Azonban ha

Φ

túlságosan nagy, a mozsár nem tud működni. Feltételezve, hogy az emelő mozgása harmonikus oszcillátornak tekinthető, becsüld meg azt a minimális

Φ_{2}

vízhozamot, amelynél a rizshántoló mozsár nem működik.

2. feladat. Cserenkov-sugárzás és gyűrűs képalkotáson alapuló számláló
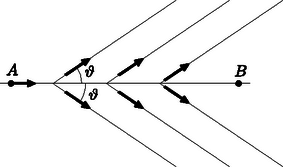
A fény vákuumban

c

sebességgel terjed. Semmiféle részecske nem mozoghat ennél a

c

sebességnél gyorsabban. Azonban lehetséges, hogy valamely átlátszó közegben mozgó részecske

v

sebessége nagyobb, mint a közegbeli

\frac{c}{n}

fénysebesség, ahol

n

a közeg (abszolút) törésmutatója. Kísérletileg 1934-ben P. A. Cserenkov észlelte, majd elméletileg 1937-ben I. J. Tamm és I. M. Frank bizonyította, hogy ha egy töltött részecske

n

törésmutatójú átlátszó közegben

v

sebességgel mozog, és teljesül, hogy

v > \frac{c}{n}

, akkor a részecske fényt bocsát ki; ez az úgynevezett Cserenkov-sugárzás.

A sugárzás iránya a részecske pályájával

\begin{matrix} ϑ = arccos \frac{1}{β n} \end{matrix}

(1)

szöget zár be, ahol

β = \frac{v}{c}

1. A fenti tény megállapítása céljából tekintsünk egy részecskét, mely egyenes pályán állandó

v > \frac{c}{n}

sebességgel mozog. A

t = 0

időpontban a részecske az

A

pontban van, míg a

t_{1}

pillanatban a

B

pontban. Mivel a probléma az

A B

tengelyre nézve forgásszimmetrikus, elegendő csupán egyetlen olyan síkban vizsgálni a fény terjedését, amely tartalmazza az

A B

tengelyt.
Bármely

A

és

B

közti

C

pontban a részecske gömbhullámokat bocsát ki, melyek

\frac{c}{n}

sebességgel terjednek. A hullámfront egy adott

t

időpillanatban a burkolója (közös érintő görbéje) ezeknek a gömbhullámoknak.
1.1. Határozd meg a hullámfrontot egy

t_{1}

időpillanatban, és rajzold be a hullámfrontnak egy, a részecske pályáját tartalmazó síkkal való metszetét!
1.2. Fejezd ki a hullámfront metszete és a részecske pályája között mérhető

φ

szöget

n

és

β

segítségével!

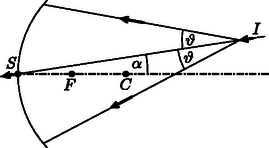
2. Tekintsük

v > \frac{c}{n}

sebességgel mozgó részecskék nyalábját, melyre teljesül, hogy a nyaláb

I S

egyenese és a sugárzás kúpja közti

ϑ

szög kicsi. (Lásd az ábrát!) A nyaláb útjában, az

S

pontban egy

C

középpontú,

f

fókusztávolságú homorú gömbtükör helyezkedik el úgy, hogy az

S C

és az

S I

egyenesek közti

α

szög szintén kicsiny. A tükörről visszavert fény a tükör fókuszsíkjában gyűrű alakú képet alkot. Igazold ezt az állítást egy vázlatos ábra segítségével! Add meg a gyűrű

r

sugarát és középpontjának

O

helyét!

Az itt ismertetett elrendezést a gyűrűs képalkotáson alapuló Cserenkov-számlálókban (Ring Imaging Cherenkov Counter, RICH) használják, és azt a közeget, amiben a részecskék haladnak, sugárzó közegnek nevezik.
Megjegyzés: Ennek a feladatnak minden kérdésében az

α

és

ϑ

szögben másod- vagy ennél magasabb rendű tagokat hanyagoljuk el.

3. Egy ismert,

p = 10, 0

GeV/c impulzusú részecskéket tartalmazó nyaláb háromféle különböző részecskét tartalmaz: protont, kaont és piont, melyek nyugalmi tömege rendre

M_{p} = 0, 94 GeV/c^{2}

M_{κ} = 0, 50 GeV/c^{2}

és

M_{π} = 0, 14 GeV/c^{2}

. Emlékeztetünk rá, hogy mind

p c

, mind pedig

M c^{2}

energia dimenziójú mennyiség, és 1 eV az az energia, amelyre egy elektron 1 V feszültséggel való gyorsítás hatására tesz szert. További mértékegységek:

1 GeV =10^{9}

eV, valamint

1 MeV =10^{6}

eV.
A részecskenyaláb

P

nyomású levegőn, mint sugárzó közegen halad át. A levegő

n

törésmutatója a következő módon függ (az atmoszférákban mért)

P

nyomástól:

\begin{matrix} n = 1 + a P, ahol a = 2, 7 \cdot 10^{- 4} atm^{- 1}. \end{matrix}

3.1. Határozd meg mindhárom részecsketípus esetén azt a minimális

P_{{min}_{}^{}}

levegőnyomást, amely fölött a Cserenkov-sugárzás kialakulhat.
3.2. Határozd meg azt a

P_{\frac{1}{2}}

nyomást, amely mellett a kaonokhoz tartozó gyűrű sugara éppen fele a pionokhoz tartozó gyűrű sugarának! Számold ki ebben az esetben a

ϑ_{κ}

és

ϑ_{π}

szögeket is!
Ezen a nyomáson megfigyelhető-e a protonokhoz tartozó gyűrű?

4. Most tegyük fel, hogy a részecskenyaláb nem teljesen monokromatikus; a részecskék impulzusa egy

10

GeV/c körül koncentrált,

Δ p

félértékszélességű eloszlást alkot. Ennek következtében a gyűrűk kiszélesednek, és a

ϑ

szög eloszlásának félértékszélessége

Δ ϑ

. A sugárzó közeg (levegő) nyomása a 3.2. pontban meghatározott

P_{\frac{1}{2}}

érték.
4.1. Határozd meg

\frac{Δ ϑ_{κ}}{Δ p}

és

\frac{Δ ϑ_{π}}{Δ p}

-t, azaz a

\frac{Δ ϑ}{Δ p}

hányados értékét kaon és pion esetén!
4.2. Amennyiben a két gyűrű közti

ϑ_{π} - ϑ_{κ}

szögeltérés nagyobb, mint a félértékszélességek

Δ ϑ = Δ ϑ_{κ} + Δ ϑ_{π}

összegének 10-szerese, tehát ha

ϑ_{π} - ϑ_{κ} > 10 Δ ϑ

, akkor a két gyűrűt jól el lehet különíteni egymástól. Határozd meg azt a maximális

Δ p

értéket, amely mellett a két gyűrű még jól elkülöníthető!

5. Cserenkov a nevéről elnevezett jelenséget először egy vízzel telt palackban figyelte meg, mely radioaktív forrás közelében helyezkedett el. Szemével érzékelte, hogy a palackban levő víz fényt bocsát ki.
5.1. Határozd meg azt a

T_{{min}_{}^{}}

minimális mozgási energiát, amely mellett egy

M

nyugalmi tömegű, vízben haladó részecske Cserenkov-sugárzást bocsát ki! A víz törésmutatója

n = 1, 33

.
5.2. Tudjuk, hogy a Cserenkov által használt sugárforrás vagy

M_{α} = 3, 8 GeV/c^{2}

nyugalmi tömegű

α

-részecskéket (azaz hélium atommagokat) vagy

M_{e} = 0, 51 MeV/c^{2}

nyugalmi tömegű

β

-részecskéket (azaz elektronokat) bocsát ki. Határozd meg

T_{{min}_{}^{}}

számszerű értékét

α

- és

β

-részecskék esetén!
Felhasználva, hogy radioaktív sugárforrások által kibocsátott részecskék mozgási energája soha nem halad meg néhány MeV-ot, döntsd el, hogy melyik részecske hozta létre a Cserenkov által először megfigyelt sugárzást!

6. Az előző kérdésekben a Cserenkov-effektusnak a kibocsátott fény hullámhosszától való függését nem vettük figyelembe. Most tekintetbe vesszük azt a tényt, hogy a Cserenkov-sugárzásnak széles folytonos spektruma van, mely tartalmazza a látható (0,4

μ

m-től 0,8

μ

m-es hullámhosszig terjedő) tartományt is. Azt is tudjuk, hogy a látható fény tartományában a

λ

hullámhossz növelésével a sugárzó közeg

n

törésmutatója lineárisan csökken

(n - 1)

-nek 2%-ával.
6.1. Tekintsünk egy pontosan

10,0 GeV / c

impulzusú pionokból álló nyalábot, amely 6 atm nyomású levegőben halad. Határozd meg a látható tartomány két végpontjához tartozó

δ ϑ

szögeltérést!
6.2. Az előző eredmény alapján tanulmányozd kvalitatíven (nem számszerűen) a diszperzió hatását egy olyan pion-nyaláb által létrehozott gyűrűs képen, melyben a részecskék impulzusa a

p = 10 GeV/c

érték körül

Δ p = 0, 3 GeV/c

félérték-szélességgel oszlik el.
6.2.1. Határozd meg a gyűrűnek a diszperzió (azaz a törésmutató hullámhossz függése miatt bekövetkező) kiszélesedését, valamint a gyűrűnek a nyalábot alkotó részecskék impulzus-inhomogenitásából fakadó kiszélesedését!
6.2.2. Hogyan változik a gyűrű színe, miközben a gyűrű belső élétől a külső él felé haladunk!

3. feladat. A levegő hőmérsékletének magasság szerinti változása, a légköri stabilitás és a légszennyeződés

A levegő függőleges mozgása sok légköri folyamatért (például a felhők és egyéb kiválások kialakulásáért és a légszennyeződés szétterjedéséért) felelős. Ha a légkör stabil, akkor a függőleges mozgás nem valósulhat meg; a levegőben lévő szennyeződések összegyűlnek a kibocsátás helye közelében, nem terjednek szét, nem hígulnak fel. Instabil légkör esetén azonban a levegő függőleges mozgása elősegíti a légszennyeződések függőleges szétterjedését. Emiatt a szennyezők koncentrációja nem csak a kibocsátó források erősségétől, hanem a légkör stabilitásától is függ.
A levegő stabilitását a meteorológiában használatos elemi ,,levegőcsomag'' (air parcel) fogalmának a használatával fogjuk meghatározni, összehasonlítva az adiabatikus állapotváltozás közben emelkedő vagy süllyedő elemi levegőcsomag hőmérsékletét a környező levegő hőmérsékletével. Látni fogjuk, hogy sok esetben a légszennyeződést tartalmazó, a felszínről felfelé emelkedő elemi levegőcsomag nyugalmi állapotba jut bizonyos magasságban, amit keveredési magasságnak nevezünk. Minél nagyobb a keveredési magasság, annál alacsonyabb a légszennyezés koncentrációja. Meg fogjuk határozni a keveredési magasságot és a szén-monoxid koncentrációt, amit egy reggeli csúcsforgalmi helyzetben Hanoi belvárosában a motorbiciklik bocsátanak ki egy olyan esetben, amikor 119 m magasság felett hőmérsékinverzió (amikor a levegő hőmérséklete felfelé növekszik) következtében a függőleges keveredés nem folytatódhat.
A levegőt tekintsük kétatomos ideális gáznak, melynek moláris tömege:

μ = 29

g/mol.
Kvázi-egyensúlyi adiabatikus folyamatban teljesül a

p V^{γ} = állandó

összefüggés, ahol

γ = \frac{c_{p}}{c_{V}}

a gáz fajhőhányadosa.
A következő adatokat használhatod:
Az egyetemes gázállandó:

R = 8, 31 J/(mol\cdotK)

.
A légköri nyomás a földfelszínen:

p_{0} = 101, 3

kPa.
Az állandónak tekinthető gravitációs gyorsulás:

g = 9, 81 m/s^{2}

.
A levegő mólhője állandó nyomáson:

c_{p} = \frac{7}{2} R

.
A levegő mólhője állandó térfogaton:

c_{V} = \frac{5}{2} R

.
Matematikai útmutatás:

\begin{matrix} \int \frac{d x}{A + B x} = \frac{1}{B} \int \frac{d (A + B x)}{A + B x} = \frac{1}{B} ln (A + B x) . \end{matrix}

a)

b)

\frac{d x}{d t} + A x = B

differenciálegyenlet (ahol

A

és

B

állandók) megoldása

\begin{matrix} x (t) = x_{1} (t) + \frac{B}{A}, \end{matrix}

ahol

x_{1} (t)

\frac{d x}{d t} + A x = 0

differenciálegyenlet megoldása.

\begin{matrix} {lim}_{x \to \infty}^{} {(1 + \frac{1}{x})}^{x} = e . \end{matrix}

c)

1. A levegő hőmérsékletének magasság szerinti változása.
1.1. Tegyük fel, hogy a légkör hőmérséklete mindenhol azonos, értéke

T_{0}

. Határozd meg, hogyan függ a légkör

p

nyomása a

z

magasságtól!
1.2. Tegyük fel, hogy a légkör hőmérséklete a következő összefüggés szerint változik a magassággal:

\begin{matrix} T (z) = T (0) - Λ z, \end{matrix}

ahol

Λ

egy állandó, amit a légkör hőmérsékletcsökkenési sebességének nevezünk (a függőleges hőmérsékletgradiens:

- Λ

).
1.2.1. Határozd meg ebben az esetben is, hogyan függ a légkör

p

nyomása a

z

magasságtól!
1.2.2. Szabad áramlás (konvekció) következik be, ha a levegő sűrűsége növekszik a magassággal. Milyen

Λ

értékek esetén valósul meg szabad áramlás?

2. Elemi levegőcsomag hőmérsékletének változása függőleges mozgás közben.
Tekintsünk egy elemi levegőcsomagot, ami fel-le mozog a légkörben. Az elemi levegőcsomag számottevő kiterjedésű levegőtömeg, néhány méter nagyságú, amit független termodinamikai egységként kell kezelnünk, azonban mégis olyan kicsiny, hogy a hőmérsékletét azonosnak, homogénnek tekinthetjük. Egy elemi levegőcsomag függőleges mozgását kváziadiabatikus folyamatként tárgyalhatjuk, azaz a környező levegővel való hőcserét elhanyagolhatjuk. Ha a levegőcsomag emelkedik a légkörben, akkor kitágul és lehűl. Következésképpen, ha lefelé mozog, akkor a növekvő külső nyomás összenyomja a levegőt a csomagon belül, és hőmérséklete emelkedni fog.
Ha a levegőcsomag mérete nem nagy, akkor feltehetjük, hogy a levegőcsomag határán és belsejében a nyomás mindenhol ugyanakkora, és megegyezik a

p (z)

légköri nyomás értékkel, ahol

z

a csomag középpontjának magassága. A csomag hőmérséklete is a csomag minden pontjában ugyanakkorának tekinthető. Ez a hőmérséklet ‐ amit

T_{csomag} (z)

-vel jelölünk ‐ általában különbözik a környező levegő

T (z)

hőmérsékletétől. A 2.1., valamint a 2.2. pontokban a

T (z)

függvényt adottnak tekinthetjük, melynek konkrét formája nem ismert.
2.1. A csomag

T_{csomag}

hőmérsékletének változását a magasság szerint a következő módon adhatjuk meg:

\frac{d T_{csomag}}{d z} = - G

. Vezess le egy formulát a

G

kifejezésre!
2.2. Tekintsük azt a különleges légköri állapotot, amikor bármely

z

magasságban a légkör

T

hőmérséklete megegyezik az elemi levegőcsomag

T_{csomag}

hőmérsékletével:

T (z) = T_{csomag} (z)

. Használjuk ilyenkor a

Γ

jelölést

G

helyett, vagyis

\begin{matrix} Γ = - \frac{d T_{csomag}}{d z}, ha T (z) = T_{csomag} (z) . \end{matrix}

Γ

neve: száraz adiabatikus csökkenési sebesség.
2.2.1. Határozz meg egy formulát a

Γ

kifejezésre!
2.2.2. Számítsd ki

Γ

számszerű értékét!
2.2.3. Add meg ebben az esetben a

T (z)

légköri hőmérséklet kifejezését a magasság függvényében!
2.3. Tegyük fel, hogy a légkör hőmérséklete a következő összefüggés szerint változik a magassággal:

T (z) = T (0) - Λ z

, ahol

Λ

egy állandó. Határozd meg az elemi levegő csomag

T_{csomag} (z)

hőmérsékletének függését a

z

magasságtól!
Add meg a

T_{csomag} (z)

kifejezés közelítő értékét, ha

| Λ \cdot z | ≪ T (0)

és

T (0) \approx T_{csomag}

3. A légköri stabilitás.
Ebben a részben feltesszük, hogy

T

lineárisan változik a magassággal.
3.1. Tekintsünk egy elemi levegőcsomagot, amely kezdetben egyensúlyban van a környező levegővel

z_{0}

magasságban, azaz hőmérséklete ugyanolyan

T (z_{0})

értékű, mint a környező levegő. Ha a levegőcsomag lassan felfelé vagy lefelé mozog, a következő három eset egyikének teljesülnie kell:
‐ A levegőcsomag visszajut az eredeti

z_{0}

magasságba, a levegőcsomag egyensúlya stabil (biztos). A légkört ekkor stabilnak tekinthetjük.
‐ A levegőcsomag folytatja mozgását a megkezdett irányba, a levegőcsomag egyensúlya instabil (bizonytalan). A légkör ilyenkor instabil.
‐ A levegőcsomag megmarad az új helyzetében, a levegőcsomag egyensúlya közömbös (indifferens). A légkört semlegesnek nevezzük.
Milyen feltételnek kell

Λ

értékére teljesülnie, hogy a légkör stabil, instabil, illetve semleges legyen?
3.2. A levegőcsomag talajon mérhető

T_{csomag} (0)

hőmérséklete legyen magasabb, mint a környező levegő

T (0)

hőmérséklete. Ilyenkor a felhajtóerő emelni kezdi a levegőcsomagot. Vezess le egy olyan kifejezést, ami megmondja, hogy a levegőcsomag mekkora maximális magasságba emelkedik stabil légkör esetén! A kifejezésben a hőmérsékleteken kívül csak

Λ

és

Γ

szerepeljen.

4. A keveredési magasság.
4.1. Az 1. táblázat egy meteorológiai léggömb hőmérséklet adatait tartalmazza, amelyeket Hanoiban mértek egy novemberi napon reggel 7:00 órakor. A hőmérséklet magasságtól való függését jó közelítéssel a

T (z) = T (0) - Λ z

formulával lehet leírni, ahol a

Λ

hőmérsékletcsökkenési sebesség a

0 < z < 96

96 m < z < 119 m

, valamint a

119 m < z < 215 m

szakaszokon más és más konstans.

\begin{matrix} Magasság & Hőmérséklet \\ [m] & [^{\circ}C] \\ 5 & 21,5 \\ 60 & 20,6 \\ 64 & 20,5 \\ 69 & 20,5 \\ 75 & 20,4 \\ 81 & 20,3 \\ 90 & 20,2 \\ 96 & 20,1 \\ 102 & 20,1 \\ 109 & 20,1 \\ 113 & 20,1 \\ 119 & 20,1 \\ 128 & 20,2 \\ 136 & 20,3 \\ 145 & 20,4 \\ 153 & 20,5 \\ 159 & 20,6 \\ 168 & 20,8 \\ 178 & 21,0 \\ 189 & 21,5 \\ 202 & 21,8 \\ 215 & 22,0 \\ 225 & 22,1 \\ 234 & 22,2 \\ 246 & 22,3 \\ 257 & 22,3 \end{matrix}

1. táblázat. A meteorológiai léggömb hőmérséklet adatai, melyeket Hanoiban mértek egy novemberi napon reggel 7:00 órakor

Tegyük fel, hogy egy

T_{csomag} (0) = 22^{\circ}

C hőmérsékletű levegőcsomag emelkedni kezd a föld felszínéről. Az 1. táblázat adatainak felhasználásával, és a fenti lineáris közelítés használatával számítsd ki a levegőcsomag hőmérsékletét a 96 m-es és a 119 m-es magasságok között!
4.2. Határozd meg a levegőcsomag által elérhető maximális

H

magasságot, és a levegőcsomag

T_{csomag} (H)

hőmérsékletét!
A

H

magasságot keveredési magasságnak nevezzük. A föld felszínéről érkező légszennyeződések ebben a rétegben keveredhetnek a légköri levegővel (például szelek, örvények stb. útján), és így a levegőcsomagban a szennyeződések felhígulhatnak.

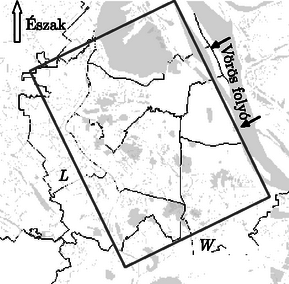
5. Szén-monoxid szennyezés (CO) becslése egy reggeli motorbiciklis csúcsforgalmi órában Hanoiban.
Hanoi belvárosát egy téglalappal közelíthetjük, melynek

L

és

W

oldalát az ábra mutatja, egyik oldalán a Vörös folyó dél-nyugati partjával.

A becslések szerint a reggeli csúcsforgalomban 7-től 8 óráig

8 \cdot 10^{5}

motorbicikli van az utakon, melyek mindegyike átlagosan 5 km utat tesz meg, és közben kilométerenként 12 g szén-dioxidot (CO) bocsát ki. A CO szennyeződés mennyiségét időben egyenletes kibocsátásúnak tekinthetjük, a csúcsforgalom alatt állandó

M

mértékűnek. Ugyanakkor a tiszta észak-keleti szél

u

sebességgel fúj a Vörös folyóra merőlegesen (azaz merőlegesen a téglalap

L

oldalára), és ugyanezzel a sebességgel hagyja el a várost, miközben magával viszi a CO-val szennyezett levegő egy részét.
Használjuk a következő durva, közelítő modellt:

$•$	A CO gyorsan szétoszlik a keveredési réteg teljes térfogatában Hanoi belvárosa felett, így a $t$ időpillanatban a $C (t)$ CO koncentráció állandónak tekinthető az $L$ , $W$ és $H$ méretekkel jellemezhető téglatest alakú doboz belsejében.

$•$	A dobozba befújó szél tiszta, feltehetjük, hogy nem tartalmaz szennyezést, továbbá azt is feltételezhetjük, hogy nem távozik szennyeződés a doboz széllel párhuzamos oldalain át.

$•$	7 óra előtt a levegő CO koncentrációja elhanyagolható.

5.1. Határozd meg azt a differenciálegyenletet, ami megadja a

C (t)

CO koncentráció értékét az idő függvényében!
5.2. Írd le a

C (t)

CO koncentrációra kapott egyenlet megoldását, azaz add meg a

C (t)

függvényt!
5.3. Számítsd ki a CO koncentráció 8 órára vonatkozó számszerű értékét!
Adatok:

L = 15

km,

W = 8

km,

u = 1

m/s.

¹ A hivatalos megoldást és a mérési feladatot a KöMaL novemberi számában ismertetjük.
A feladatok kidolgozására 5 óra állt rendelkezésre.