Kezdőlap


Cím:	A 49. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Szerző(k):	Eisenberger András , Kiss Viktor , Korándi Dániel , Kornis Kristóf , Lovász László Miklós , Tomon István
Füzet:	2008/október, 387 - 394. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

A szerkesztőség

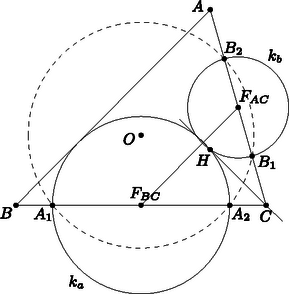
1. A hegyesszögű

A B C

háromszög magasságpontja

H

. Az a

H

-n átmenő kör, amelynek középpontja a

B C

szakasz felezőpontja, a

B C

egyenest

A_{1}

-ben és

A_{2}

-ben metszi. Hasonlóan, az a

H

-n átmenő kör, amelynek középpontja a

C A

szakasz felezőpontja, a

C A

egyenest

B_{1}

-ben és

B_{2}

-ben metszi, az a

H

-n átmenő kör pedig, amelynek középpontja az

A B

szakasz felezőpontja, az

A B

egyenest

C_{1}

-ben és

C_{2}

-ben metszi. Bizonyítsuk be, hogy az

A_{1}

A_{2}

B_{1}

B_{2}

C_{1}

C_{2}

pontok egy körön fekszenek.

Kornis Kristóf megoldása. Legyenek rendre

k_{a}

k_{b}

k_{c}

A_{1} A_{2}

B_{1} B_{2}

C_{1} C_{2}

átmérőjű körök;

F_{A B}

F_{B C}

F_{C A}

rendre az

A B

B C

C A

szakaszok felezőpontjai. Két kör hatványvonala nyilvánvalóan merőleges a középpontjaikat összekötő egyenesre. Emiatt

k_{a}

és

k_{b}

hatványvonala, és

C H

is merőleges

F_{B C} F_{A C}

-re, de mivel mindkettőnek eleme

H

, e két egyenes egybeesik, azaz a

C

pontnak a

k_{a}

és

k_{b}

körökre vonatkozó hatványa megegyezik. Vagyis

\begin{matrix} C A_{1} \cdot C A_{2} = C B_{1} \cdot C B_{2} . \end{matrix}

Azaz

A_{1}

A_{2}

B_{1}

B_{2}

egy körön fekszenek, melynek középpontja az

A_{1} A_{2}

és a

B_{1} B_{2}

szakaszok felezőmerőlegeseinek metszéspontja. Ezek a felezőmerőlegesek viszont éppen egybeesnek az oldalfelező merőlegesekkel, azaz az

A_{1} A_{2} B_{1} B_{2}

kör középpontja

O

, ha

O

a körülírt kör középpontja, tehát

\begin{matrix} O A_{1} = O A_{2} = O B_{1} = O B_{2} . \end{matrix}

Hasonlóan bizonyíthatjuk, hogy

\begin{matrix} O A_{1} & = O A_{2} = O C_{1} = O C_{2} \Rightarrow \\ \Rightarrow O A_{1} & = O A_{2} = O B_{1} = O B_{2} = \\ = O C_{1} = O C_{2} . \end{matrix}

(a)

Mutassuk meg, hogy az

\begin{matrix} \frac{x^{2}}{{(x - 1)}^{2}} + \frac{y^{2}}{{(y - 1)}^{2}} + \frac{z^{2}}{{(z - 1)}^{2}} \geq 1 \end{matrix}

egyenlőtlenség teljesül minden olyan,

1

-től különböző

x

y

z

valós számok esetén, amelyekre

x y z = 1

(b)

Mutassuk meg, hogy van végtelen sok olyan,

1

-től különböző racionális számokból álló

x, y, z

számhármas, amelyre

x y z = 1

, és amelyre a fenti egyenlőtlenségben az egyenlőség esete áll fenn.

Korándi Dániel megoldása. Legyen

a = \frac{x}{1 - x}

b = \frac{y}{1 - y}

c = \frac{z}{1 - z}

\begin{matrix} a b c & = \frac{x y z}{(1 - x) (1 - y) (1 - z)} = \frac{1}{(1 - x) (1 - y) (1 - z)} = \\ = (a + 1) (b + 1) (c + 1), \end{matrix}

azaz

\begin{matrix} (a + 1) (b + 1) (c + 1) - a b c = a b + a c + b c + a + b + c + 1 = 0. \end{matrix}

(1)

Ugyanakkor

\begin{matrix} {(a + b + c + 1)}^{2} & = a^{2} + b^{2} + c^{2} + 1 + 2 (a b + a c + b c + a + b + c) = & (2) \\ = a^{2} + b^{2} + c^{2} - 1. \end{matrix}

Azt kaptuk tehát, hogy

a^{2} + b^{2} + c^{2} - 1 \geq 0

, a feladat

(a)

része pedig pont ezt kérdezi.
A

(b)

rész végtelen sok olyan

(x, y, z)

racionális számokból álló hármast keres, amire

x y z = 1

és felhasználva (2)-t,

a + b + c + 1 = 0

. (1) szerint

a + b + c + 1 = 0

akkor és csak akkor teljesül, ha

a b + a c + b c = 0

, ami ekvivalens

\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0

-val, mivel

a b c \neq 0

. (

x

y

z

egyike sem 0, mivel a szorzat 1. Ekkor viszont

a

b

c

sem lehet 0.) Visszaírva

a

b

c

értékét:

\begin{matrix} \frac{1 - x}{x} + \frac{1 - y}{y} + \frac{1 - z}{z} = 0. \end{matrix}

3-at hozzáadva mindkét oldalhoz:

\begin{matrix} \frac{1}{x} + \frac{1}{y} + \frac{1}{z} = y z + x z + x z = 3. \end{matrix}

Azaz olyan számhármasokat keresünk, amire

x y z = 1

és

x y + x z + y z = 3

, valamint

x, y, z \neq 1

.
Írjunk be

x

helyébe

\frac{1}{y z}

-t.

\frac{1}{z} + \frac{1}{y} + y z = 3

racionális megoldásait keressük. Szorozva

y z

-vel egy másodfokú egyenletet kapunk

y

-ra:

\begin{matrix} z^{2} y^{2} + (1 - 3 z) y + z = 0. \end{matrix}

Olyan racionális

z

-t keresünk, amire ennek az egyenletnek a gyökei is racionálisak, ehhez az kell, hogy a diszkrimináns egy racionális szám négyzete legyen:

\begin{matrix} D & = {(1 - 3 z)}^{2} - 4 z^{3} = - 4 z^{3} + 9 z^{2} - 6 z + 1 = (z - 1) (- 4 z^{2} + 5 z - 1) = \\ = {(z - 1)}^{2} (1 - 4 z) . \end{matrix}

Mivel

y

racionális, azért

{(z - 1)}^{2}

egy racionális szám négyzete, így szükséges, hogy

1 - 4 z

is egy racionális szám négyzete legyen. Ehhez viszont tetszőleges racionális

q

-ra elég

z = \frac{1 - q^{2}}{4}

-et választani. Ekkor

y

is racionális lesz, s így

x = \frac{1}{y z}

is. Tehát van végtelen sok racionális megoldás. Ezzel igazoltuk a

(b)

részt is.

3. Bizonyítsuk be, hogy van végtelen sok olyan

n

pozitív egész szám, amelyre

(n^{2} + 1)

-nek van olyan prímosztója, ami nagyobb, mint

2 n + \sqrt[]{2 n}

Lovász László Miklós megoldása. A bizonyítandó állítás következik az alábbi állításból:
Végtelen sok

p

prím van, amihez létezik olyan

n

, hogy

\begin{matrix} 2 n + \sqrt[]{2 n} < p, és p ∣ n^{2} + 1. \end{matrix}

Ha ugyanis csak véges sok megfelelő

n

lenne, akkor, mivel

(n^{2} + 1)

-nek véges sok különböző prímosztója van, csak véges sok megfelelő

p

lenne.
Ismert, hogy végtelen sok

p = 4 k + 1

alakú prím van, és hogy ezekre létezik olyan

n

, amire

p ∣ n^{2} + 1

. Legyen

p > 20

egy

4 k + 1

alakú prím. Nyilván létezik ekkor ilyen

n

(0, p)

intervallumban¹. Ha

n > \frac{p}{2}

, akkor

p - n < \frac{p}{2}

, így

\begin{matrix} {(p - n)}^{2} + 1 \equiv n^{2} + 1 \equiv 0 (p) . \end{matrix}

Tehát van megfelelő pozitív egész

n

, amire

n < \frac{p}{2}

, vagyis

2 n < p

.
Legyen

n = \frac{p - k}{2}

. Mivel

p

páratlan,

k > 0

\begin{matrix} {(\frac{p - k}{2})}^{2} + 1 & \equiv 0 (p), \\ {(p - k)}^{2} + 4 & \equiv 0 (p), \\ k^{2} + 4 & \equiv 0 (p) . \end{matrix}

k^{2} > 0, 4 > 0 \Rightarrow k^{2} + 4 > 0

, tehát

k^{2} + 4 \geq p

, amiből

k \geq \sqrt[]{p - 4}

. Ekkor tehát

\begin{matrix} n = \frac{p - k}{2} \leq \frac{p - \sqrt[]{p - 4}}{2}, \end{matrix}

vagyis

\begin{matrix} 2 n \leq p - \sqrt[]{p - 4}, 2 n + \sqrt[]{p - 4} \leq p, p - 4 \geq 2 n + \sqrt[]{p - 4} - 4. \end{matrix}

Mivel

p > 20

\sqrt[]{p - 4} > 4

, amiből

p - 4 > 2 n \Rightarrow \sqrt[]{p - 4} > \sqrt[]{2 n}

. Azt kaptuk tehát, hogy

\begin{matrix} p \geq \sqrt[]{p - 4} + 2 n > \sqrt[]{2 n} + 2 n . \end{matrix}

Tehát ha

p

elég nagy, létezik hozzá megfelelő

n

, így mivel végtelen sok

4 k + 1

alakú prím van, végtelen sok megfelelő

p

van, és ezért végtelen sok megfelelő

n

van.

4. Határozzuk meg az összes olyan

f : (0, \infty) \to (0, \infty)

függvényt (

f

tehát a pozitív valós számok halmazából a pozitív valós számok halmazába képez), amelyre

\begin{matrix} \frac{{(f (w))}^{2} + {(f (x))}^{2}}{f (y^{2}) + f (z^{2})} = \frac{w^{2} + x^{2}}{y^{2} + z^{2}} \end{matrix}

teljesül, valahányszor

w

x

y

z

olyan pozitív valós számok, amelyekre fennáll:

w x = y z

Kiss Viktor megoldása. Helyettesítsük be

w = x = y = z = 1

-et. Teljesül az

w x = y z

feltétel, tehát

\begin{matrix} \frac{2 f^{2} (1)}{2 f (1)} = \frac{1^{2} + 1^{2}}{1^{2} + 1^{2}} = 1. \end{matrix}

f (1) > 0

, tehát egyszerűsíthetünk vele, kapjuk, hogy

f (1) = 1

. Ezután helyettesítsünk be

w = 1

x = a

y = z = \sqrt[]{a}

-t, ahol

a

tetszőleges pozitív valós szám. Teljesül, hogy

w x = y z

, tehát

\begin{matrix} \frac{f^{2} (1) + f^{2} (a)}{2 f (a)} = \frac{1 + f^{2} (a)}{2 f (a)} = \frac{1 + a^{2}}{2 a} . \end{matrix}

f (a)

és

a

is pozitív, tehát szorozhatunk velük, kapjuk, hogy

\begin{matrix} a (1 + f^{2} (a)) = f (a) (1 + a^{2}), \end{matrix}

azaz

\begin{matrix} f^{2} (a) \cdot a - f (a) (1 + a^{2}) + a = 0. \end{matrix}

Ez másodfokú egyenlet

f (a)

-ra, megoldásai a következők:

\begin{matrix} f (a) = \frac{1 + a^{2} \pm \sqrt[]{{(1 + a^{2})}^{2} - 4 a^{2}}}{2 a} = \frac{1 + a^{2} \pm \sqrt[]{1 + a^{4} - 2 a^{2}}}{2 a} . \end{matrix}

a \geq 1

, akkor

\begin{matrix} f (a) = \frac{1 + a^{2} \pm \sqrt[]{{(a^{2} - 1)}^{2}}}{2 a} = \frac{1 + a^{2} \pm (a^{2} - 1)}{2 a} = a vagy \frac{1}{a} . \end{matrix}

a < 1

, akkor

\begin{matrix} f (a) = \frac{1 + a^{2} \pm \sqrt[]{{(1 - a^{2})}^{2}}}{2 a} = \frac{1 + a^{2} \pm (1 - a^{2})}{2 a} = a vagy \frac{1}{a} . \end{matrix}

Tehát megkaptuk, hogy

f (a)

értéke tetszőleges

a

-ra

a

vagy

\frac{1}{a}

. Tegyük fel, hogy létezik

a, b \neq 1

, hogy

\begin{matrix} f (a) = a és f (b) = \frac{1}{b} . \end{matrix}

Helyettesítsünk be

w = a

x = b

y = 1

z = a b

-t.
I. eset:

f (a^{2} b^{2}) = a^{2} b^{2}

. Ekkor

\begin{matrix} \frac{f^{2} (a) + f^{2} (b)}{f (1^{2}) + f (a^{2} b^{2})} = \frac{a^{2} + \frac{1}{b^{2}}}{1 + a^{2} b^{2}} = \frac{a^{2} + b^{2}}{1 + a^{2} b^{2}}, \end{matrix}

ami nem lehet, hiszen

b \neq 1

és pozitív, tehát

b^{2} \neq \frac{1}{b^{2}}

.
II. eset:

f (a^{2} b^{2}) = \frac{1}{a^{2} b^{2}}

. Ekkor

\begin{matrix} \frac{f^{2} (a) + f^{2} (b)}{f (1^{2}) + f (a^{2} b^{2})} = \frac{a^{2} + \frac{1}{b^{2}}}{1 + \frac{1}{a^{2} b^{2}}} = \frac{a^{4} b^{2} + a^{2}}{a^{2} b^{2} + 1} = \frac{a^{2} + b^{2}}{1 + a^{2} b^{2}}, \end{matrix}

ami csak akkor teljesülhetne, ha

a^{4} = 1

teljesülne (hiszen

a

pozitív), de ez nem igaz. Tehát megkaptuk, hogy vagy minden

a \neq 1

-re

f (a) = a

, vagy minden

a \neq 1

-re

f (a) = \frac{1}{a}

(mivel

f (1) = 1

, azért a két szóba jövő függvény az

f (x) = x

és az

f (x) = \frac{1}{x}

). Most belátjuk, hogy mindkét függvény teljesíti a feladat feltételeit. Ha az

f (x) = x

-et tekintjük, akkor

\begin{matrix} \frac{f^{2} (w) + f^{2} (x)}{f (y^{2}) + f (z^{2})} = \frac{w^{2} + x^{2}}{y^{2} + z^{2}} \end{matrix}

triviálisan teljesül.
Ha

f (x) = \frac{1}{x}

, akkor

\begin{matrix} \frac{f^{2} (w) + f^{2} (x)}{f (y^{2}) + f (z^{2})} & = \frac{\frac{1}{w^{2}} + \frac{1}{x^{2}}}{\frac{1}{y^{2}} + \frac{1}{z^{2}}} & | \cdot \frac{w^{2} x^{2}}{y^{2} z^{2}} \\ \frac{x^{2} y^{2} z^{2} + w^{2} y^{2} z^{2}}{z^{2} x^{2} w^{2} + y^{2} x^{2} w^{2}} & = \frac{(x^{2} + w^{2}) y^{2} z^{2}}{(y^{2} + z^{2}) x^{2} w^{2}} = \frac{x^{2} + w^{2}}{y^{2} + z^{2}} & (hiszenw x = y z). \end{matrix}

Tehát csak az

f (x) = x

és

f (x) = \frac{1}{x}

függvények teljesítik a feladat feltételeit, és ezek valóban teljesítik azokat.

5. Legyenek

n

és

k

pozitív egészek, amelyekre

k \geq n

és

k - n

páros szám. Adott

2 n

lámpa, amelyek

1

-től

2 n

-ig vannak számozva, és amelyek mindegyike be(kapcsolt) vagy ki(kapcsolt) állapotban lehet. Kezdetben mindegyik lámpa ki állapotban van. Lépések egy sorozatát tekintjük: egy lépés abból áll, hogy valamelyik lámpa állapotát megváltoztatjuk (be-ről ki-re vagy ki-ről be-re).
Legyen

N

az olyan,

k

lépésből álló sorozatok száma, amelyek eredményeképpen az

1

-től

n

-ig számozott lámpák bekapcsolt, az

(n + 1)

-től

2 n

-ig számozott lámpák pedig kikapcsolt állapotban lesznek.
Legyen

M

az olyan,

k

lépésből álló sorozatok száma, amelyek eredményeképpen az

1

-től

n

-ig számozott lámpák bekapcsolt, az

(n + 1)

-től

2 n

-ig számozott lámpák pedig kikapcsolt állapotban lesznek, és a sorozatban az

(n + 1)

-től

2 n

-ig számozott lámpák semelyikét sem kapcsoljuk be semmikor.
Határozzuk meg az

N / M

hányados értékét.

Eisenberger András megoldása.

N / M = 2^{k - n}

.
Alkossunk egy megfeleltetést úgy, hogy minden

M

-beli sorozatot

2^{k - n}

N

-belinek feleltetünk meg úgy, hogy minden

N

-belit pontosan egyszer kapjunk meg.
Vegyünk egy

M

-beli

m

sorozatot. (Ebben a sorozatban tehát 1-től

n

-ig minden lámpát páratlan sokszor kapcsoltunk át.) Induljunk el sorban a sorozat lépésein. Amikor olyan lámpát kapcsolnánk át (legyen az

i

. lámpa), amit

m

szerint még egy későbbi lépésben is kapcsolunk majd, akkor kétféleképp folytathatjuk: az

i

. lámpát vagy az

(n + i)

. lámpát kapcsoljuk, ezután tovább megyünk a következő lépésre. Ha nem ilyen a lépés, tehát

m

-ben már többször nem kapcsolnánk ezt a lámpát, akkor megnézzük, hogy eddig hányszor kapcsoltuk az

i

. lámpát. Ha páros sokszor, akkor most is az

i

. lámpát kapcsoljuk, ha páratlan sokszor, akkor az

(n + i)

. lámpát (itt tehát nincs választásunk). Ezzel a módszerrel a végén az

i

. lámpa biztosan be lesz kapcsolva, az

(n + i)

. pedig biztosan ki, mivel az eredeti sorozatban és most is az

i

. páratlan sokszor szerepelt, így most az

(n + i)

. lámpát biztosan páros sokszor kapcsoltuk. Mindamellett az eredeti sorozathoz hasonlóan

k

lépést hajtottunk végre, ezért az így kapott sorozat

N

eleme.
A sorozat alkotása során az első

n

lámpát legalább egyszer kapcsoltuk, így

n

olyan lépés volt, amikor valamelyiket utoljára kapcsoltuk, tehát a maradék

(k - n)

lépés volt az a fajta, ahol választásunk volt. Vagyis az

M

minden eleméhez az

N

-nek

2^{k - n}

elemét rendeltük. Már csak azt kell megmutatnunk, hogy

N

minden elemét pontosan egyszer kaptuk meg. Ez azért igaz, mert ha veszünk egy sorozatot

N

-ből, és minden olyan kapcsolás helyett, ahol az

(n + i)

. lámpát kapcsolnánk, az

i

. lámpát kapcsoljuk, akkor megkapjuk

M

-nek azt az egyetlen sorozatát, amiből ezt az

N

-beli sorozatot kaphatjuk. És az is egyértelmű, hogy melyik döntésnél hogyan kell dönteni ahhoz, hogy ezt kaphassuk.

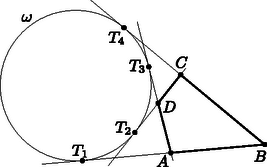
6. Legyen

A B C D

konvex négyszög, amelyben

B A \neq B C

. Jelölje

ω_{1}

, ill.

ω_{2}

A B C

, ill.

A D C

háromszögek beírt körét. Tegyük fel, hogy létezik egy olyan

ω

kör, amelyik érinti a

B A

félegyenes

A

-n túli részét és a

B C

félegyenes

C

-n túli részét, továbbá érinti az

A D

és

C D

egyeneseket. Bizonyítsuk be, hogy az

ω_{1}

és

ω_{2}

körök közös külső érintői az

ω

körön metszik egymást.

Tomon István megoldása. Lemma: Ha egy

A B C D

négyszögnél létezik az

ω

kör, akkor

\begin{matrix} A B + A D = C B + C D . \end{matrix}

Bizonyítás: Legyenek az

ω

kör érintési pontjai az oldalegyenesekkel az ábrán látható módon

T_{1}

T_{2}

T_{3}

T_{4}

. Ekkor felhasználva, hogy egy adott pontból a körhöz húzott érintőknek hossza megegyezik, azt kapjuk, hogy

\begin{matrix} B T_{4} = B T_{1} . \end{matrix}

(1)

Ezen kívül a következő egyenlőséglánc teljesül:

\begin{matrix} B T_{4} & = B C + C T_{4} = B C + C T_{2} = B C + C D + D T_{2} = B C + C D + D T_{3} = \\ = B C + C D + A T_{3} - A D = B C + C D + A T_{1} - A D = \\ = B C + C D + B T_{1} - A D - A B . \end{matrix}

Ezt összevetve (1)-gyel azt kapjuk, hogy

B C + C D = A B + A D

, s ezzel a Lemmát bebizonyítottuk.

Most térjünk rá a feladat bizonyítására. Húzzuk meg az

ω_{1}

kör

A C

-től különböző,

A C

-vel párhuzamos érintőjét, érintse ez

ω_{1}

-et az

E'

pontban.

ω_{1}

és

A C

érintési pontja legyen

E

ω_{2}

és

A C

érintési pontja

F

, ezen kívül húzzuk meg az

ω

körnek az

A C

-vel párhuzamos érintőjét, amely elválasztja

B

-t

ω

-tól, érintse ez

ω

-t a

H

pontban.
Az ismert összefüggés alapján

C E = \frac{- A B + B C + C A}{2}

és

A F = \frac{- C D + A D + A C}{2}

, tehát a Lemma alapján

C E = A F

. Ez azt jelenti, hogy

F

A B C

háromszög

A C

oldalához írt körnek az érintési pontja, tehát ha az

A C

-vel

E'

-n át húzott egyenest

B

-ből

A C

-be nyújtjuk, akkor

E'

F

-be kerül, így

B

E'

F

egy egyenesen vannak, tehát

B

E'

F

H

egy egyenesen vannak.

Legyen

H'

ω_{1}

és

ω_{2}

közös külső érintőinek metszéspontja. Ekkor a

H'

-ből az

ω_{2}

-t az

ω_{1}

körbe nagyíthatjuk, s ekkor az

F

pont az

E'

pontba megy át, így

H'

F

E'

egy egyenesen vannak. Vagyis

B

E'

F

H

H'

egy egyenesen vannak, azaz nézzük csak azt, hogy

B

F

H

H'

egy

f

egyenesen vannak. Hasonlóan, ha

D

-t tekintjük a nyújtás középpontjának, akkor

H

D

F'

E

egy egyenesen vannak. Tekintsük újra a

H'

-ből az

ω_{2}

nagyítását

ω_{1}

-be. Ekkor az

F'

pont

E

-be megy át, így

H'

F'

E

egy egyenesen vannak. Tehát

H'

H

D

E

egy

e

egyenesen vannak. A

B A \neq B C

feltétel biztosítja, hogy a

B F

egyenes nem azonos a

D E

egyenessel. Ezért az

e

és az

f

egyenesek különbözők, tehát csak egyetlen közös pontjuk van. Így szükségképpen

H = H'

, s mivel

H

rajta van a körön, így

H'

is, s ezzel az állítást bebizonyítottuk.

n

p

szerinti osztási maradéka megfelelő lesz.