Cím:	11. Román‐magyar előolimpiai fizikaverseny feladatai
Füzet:	2008/szeptember, 368 - 372. oldal	PDF  |  MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Elméleti feladatok   1. Egy $2l$ hosszúságú, $2m$ tömegű igen hajlékony és nyújthatatlan kötél egyik végét ideálisnak tekinthető erőmérő eszközhöz kötjük, a másik végét pedig addig emeljük, amíg a kötél két vége lényegében ugyanarra a pontra kerül. Ekkor az erőmérő $mg$ erőt jelez. Ezután a kötél szabad végét elengedjük. A légellenállás elhanyagolható. $a)$ Határozzuk meg a kötél szabad végének mozgását az idő függvényében (hely‐idő függvényt kérünk)! $b)$ Határozzuk meg a kötél hajlatának mozgását az idő függvényében (hely‐idő függvényt kérünk)! $c)$ Határozzuk meg és ábrázoljuk grafikusan a kötél mozgási energiáját az idő függvényében (grafikont kérünk)! $d)$ Határozzuk meg és ábrázoljuk grafikusan az erőmérő által jelzett erőt az idő függvényében! $e)$ Számítsuk ki az erőmérő által jelzett erő időátlagát! $f)$ Összesen mennyi hő szabadul fel, ha feltételezzük, hogy amikor az egész kötél eléri a függőleges egyenes helyzetét, akkor a kötél megáll, és állva is marad? $g)$ Határozzuk meg és ábrázoljuk grafikusan a kötél felmelegedésekor a hőteljesítményt az idő függvényében! $h)$ Számítsuk ki a hőteljesítmény-idő grafikon görbe alatti területét!   2. Ebben a feladatban a mágneses tér hatását vizsgáljuk áramjárta vezetőkre. Az áram leírásakor alkalmazzuk az úgynevezett Drude-modellt, ami a vezetési elektronokat úgy írja le, hogy azok egyenletes mozgást végeznek $v_d$ (drift-) sebességgel.   I. RÉSZ: $a)$ $R$ sugarú, kör keresztmetszetű rézdrótban $I$ áram folyik. Mekkora a vezetési elektronok driftsebessége? ($R=1$ mm, $I=10$ A, a réz egy vegyértékűnek tekinthető, vagyis minden rézatom egy elektronnal járul hozzá a delokalizált vezetési elektronokhoz, a réz anyagsűrűsége: ${\rho }_{\text{anyag}}=8920\text{kg/<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$, a réz moláris tömege: $M=63\mathrm{,}54\text{g/mol}$, az elemi töltés: $q_{\text{e}}=1\mathrm{,}602\cdot {10}^{-19}$ C, az Avogadro-szám: $N_{\text{A}}=6\mathrm{,}022\cdot {10}^{23}$ 1/mol.) $b)$ Az előző alkérdésben szereplő esetben az $I$ áram következtében mekkora a mágneses indukció a vezetőn belül és kívül? (Feltehetjük, hogy az áramsűrűség mindenhol azonos. A vákuum mágneses permeábilitása: ${\mu }_0=4\pi \cdot {10}^{-7}\frac{\text{Vs}}{\text{Am}}$, a réz relatív mágneses permeábilitását 1-nek tekinthetjük.) $c)$ Mekkora és milyen irányú erő hat a vezetési elektronokra az áram saját mágneses tere miatt? $d)$ Milyen elektrosztatikus töltéseloszlás alakul ki emiatt a vezetőben? (A vákuum dielektromos állandója: ${\epsilon }_0=\frac{1}{4\pi k}$, ahol $k=8\mathrm{,}99\cdot {10}^9\frac{\text{N<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}}{\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>C</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}}$, a Coulomb-törvényben szereplő állandó.) Értékeld (kommentáld) numerikus eredményedet!   II. RÉSZ: $e)$ Ebben a részben a réz vezető alakja legyen hosszú, négyzetes hasáb. A négyzet oldaléle legyen $a$, az átfolyó áram értéke pedig ugyanúgy $I$, mint az előző részben. A vezetőre merőleges, az egyik oldallappal párhuzamos, $B$ mágneses indukciójú teret kapcsolunk be. Mekkora felületi töltéssűrűség alakul ki ennek hatására a vezetőn? ($I=10$ A, $a=1$ cm, $B=2$ T.)   III. RÉSZ: $f)$ A vezető legyen ugyanilyen réz anyagú, ugyanilyen $R$ sugarú, hosszú, egyenes henger, amelyben ugyanekkora $I$ áram folyik. A vezetőt hűtsük le a szupravezető átmeneti hőmérséklet alá, miközben gondoskodjunk arról, hogy az áram mindvégig ugyanakkora maradjon. A szupravezetők nevezetes tulajdonsága az, hogy belsejükben a mágneses tér nulla, áram tehát csak a felületükön folyhat. A felületi áramsűrűség exponenciális függvény szerint csökken a vezető belseje felé haladva, amit a $\lambda$ behatolási mélység jellemez. Ez azt jelenti, hogy a kicsiny $\lambda$ távolság után az áramsűrűség $e$-ed részére csökken ($e\approx 2\mathrm{,}718$). A behatolási mélység az elektronok $m$ tömegétől, a szupravezető elektronok $n_s$ részecskeszám-sűrűségétől, és az abszolút, illetve a relatív mágneses permeábilitástól (${\mu }_{\text{rel}}{\mu }_0)$ függ. Tudjuk továbbá azt is, hogy a behatolási mélység fordítottan arányos az elektronok $q_e$ töltésével. Dimenzióanalízis segítségével adjuk meg a behatolási mélység matematikai alakját, feltételezve, hogy a formulában a számfaktor értéke 1! $g)$ Fejezd ki az áramsűrűséget közvetlenül a szupravezető drót felületén $I$, $R$ és $\lambda$ függvényében paraméteresen (nem számszerűen)!   IV. RÉSZ: $h)$ Legyen az előzőekkel megegyező anyagú, hosszú szupravezető ($a\times b$) felületű téglalap keresztmetszetű hasáb, ahol $a\ll b$, továbbá a szélesebb oldal mentén, középtájon, vagyis nem közvetlenül a lemez szélein, a felületen az áramsűrűség legyen ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">j</span></span>}}_0$. Kapcsoljunk be egy kicsiny $\text{<span style="font-weight: bold;"><span style="font-style: italic;">B</span></span>}$ mágneses indukciójú teret, amely merőleges a vezetőre és párhuzamos a szélesebb oldallal. A mágneses tér olyan kicsiny, hogy nem szünteti meg a szupravezető viselkedést. Hogyan változik meg a szupravezetőben a szélesebb oldal közepén a felületen az áramsűrűség értéke a mágneses tér következtében? Válaszodat paraméteresen fejezd ki!   3. Etűdök adiabatikus invariánsra Adiabatikus invariáns. Ebben a feladatcsokorban olyan egydimenziós mechanikai rendszereket vizsgálunk, melyek tartalmaznak egy paramétert is. Ilyen rendszerekben sokszor igen érdekes aszimptotikus jelenség figyelhető meg: a paraméter lassú változtatása mellett két eredetileg egymástól független mennyiség egymás függvényévé válik, és úgy viselkednek, mintha valami különös megmaradási törvényt elégítenének ki. Ezeket a lassú paraméterváltozás mellett megmaradó mennyiségeket adiabatikus invariánsoknak nevezzük. Fázistér. A mechanikában fázistérnek nevezzük azt az absztrakt koordinátarendszert, melynek tengelyein az úgynevezett általános koordinátákat és általános impluzusokat ábrázoljuk. A következő problémákban a fázistér kétdimenziós. Lineáris mozgás esetén az általános koordináta egy referenciaponttól számított elmozdulás, míg az általános impulzus a lendület. Körmozgás esetén az általános koordináta egy referenciaponttól számított szögelfordulás, míg az általános impulzus a perdület. Falak közt pattogó labda. Ebben a feladatban a gravitáció hatásától eltekintünk. Az $m$ tömegű pontszerű test két, kezdetben rögzített, egymástól $h_0$ távolsgára levő rugalmas fal között ,,pattog''. A test egydimenziós mozgást végez, és mindig tökéletesen rugalmasan ütközik a falakkal, tehát sebességének $v_0$ nagysága nem változik. Ekkor lassan elkezdjük változtatni a falak $h$ távolságát. $a)$ Változik-e, és ha igen, hogyan a test $v\left(h\right)$ sebessége a falak $h$ távolságának függvényében? $b)$ Ábrázoljuk a falak különböző pillanatnyi helyzetei esetén a mozgást a fázistérben! Találunk-e valamilyen geometriai invariánst (megmaradó mennyiséget) a fázistérben? $c)$ Adjuk meg a kapcsolatot a falak $h$ távolsága és a pattogó labda által a falakra kifejtett $F$ átlagos erő között! $d)$ Az eddig megoldott problémák alapján próbáljuk meg ,,levezetni'' az egyatomos ideális gáz adiabatájának állapotegyenletét! Tekintsünk $N$ darab $m$ tömegű rugalmas, pontszerű részecskét, melyek $A$ alapterületű, $h$ magasságú hengerben mozognak, ahol a $h$ magasság egy dugattyú segítségével lassan változtatható. Határozzuk meg a henger $V=Ah$ térfogata és a részecskék által keltett átlagos $p$ nyomás között a kapcsolatot! 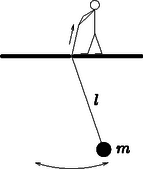(Tegyük föl, hogy a gyakori ütközések következtében a részecskék izotróp módon mozognak.) Változó hosszúságú inga. Tekintsük az $l$ hosszúságú, $m$ tömegű matematikai ingát, mely $\Phi \ll 1$ rad maximális szögkitéréssal csillapítatlanul leng.     $a)$ Adjuk meg az inga kötelét feszítő erő $\overline{K}$ időátlagát! Ezután lassan elkezdjük változtatni az inga $l$ hosszát. $b)$ Változik-e, és ha igen, hogyan a lengés $\Phi \left(l\right)$ maximális szögkitérése az inga $l$ hosszának függvényében? (Tegyük föl, hogy mindvégig $\Phi \ll 1$.) Útmutatás: Írjuk föl az ingára a munkatételt, miközben az inga hosszát $\Delta l$-lel megváltoztatjuk. A kötélerő munkájának számolásakor használjuk az előző pontban kiszámolt időátlagot. $c)$ Ábrázoljuk a mozgást különböző ingahosszak esetén a fázistérben, tehát a szögkitérés‐impulzusmomentum koordinátarendszerben! Találunk-e valamilyen geometriai invariánst (megmaradó mennyiséget) a fázistérben? Mágneses térben keringő töltés. Tekintsük az $m$ tömegű, $q$ töltésű pontszerű testet, mely $B$ nagyságú, homogénnek tekinthető mágneses térben $R$ sugarú körpályán egyenletes körmozgást végez. A mozgás nem relativisztikus. $a)$ Adjuk meg a körmozgás $\omega$ szögsebességét! Ekkor lassan elkezdjük változtatni a $B$ mágneses teret. (A tér mindvégig közel homogén marad, és iránya nem, csak nagysága változik.) $b)$ Változik-e, és ha igen, hogyan a keringés $R\left(B\right)$ sugara a mágneses tér függvényében? Találunk-e valamilyen invariánst (megmaradó mennyiséget)? (Útmutatás: Határozzuk meg, hogy változó mágneses tér esetén mennyivel változik a töltés kinetikus energiája egyetlen ,,kör'' megtétele során.)   Kísérleti forduló   Fényszórás vizsgálata kolloid oldatban Eszközök: lézer tartóval; üveghenger; detektor (kapcsolási rajz alább): elektromos kapcsolás + voltmérő; zseblámpaizzó, változtatható feszültségű adapterrel (az izzó üzemi feszültsége 3 V, néhány esetben ettől eltérően, a beállított értéken használja az adaptert!); mm-papír, mm-papír csíkok; állvány, kémcsőfogó; kolloid oldat egy főzőpohárban; orvosi fecskendő. 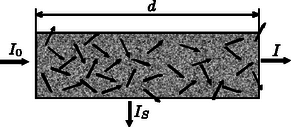Általános ismeretek Amikor fény halad át valamely közegen, akkor a kilépő $I$ fényintenzitás többnyire kisebb, mint a belépő $I_0$. A csökkenés alapvetően két folyamat, az abszorpció és a szórás következménye. További fényveszteséget okoz a határfelületeken fellépő reflexiós veszteség, amely független a réteg vastagságától.     A folyamat mikroszkopikus magyarázata: A fény elektromos mezője mozgásba hozza a részecskéket (kényszerrezgés jön létre). A kényszerrezgés fázisa a beeső hullám fázisától különbözik, ez okozza a fény közegbeli, illetve vákuumbeli sebességének különbözőségét. $a)$ Ha a beeső hullám frekvenciája megegyezik ‐ vagy legalábbis közel esik ‐ a részecskék sajátfrekvenciájához, akkor rezonancia jön létre, majd az elnyelődő energia egy részét a tér minden irányába, általában kisebb energiájú sugárzással bocsátja ki a részecske. Ez a folyamat a vizsgált közegünkben elhanyagolható. $b)$ A fényszórás a részecskék sajátfrekvenciájától eltérő frekvenciákon történik. A szórt fény frekvenciája megegyezik a beeső fény frekvenciájával, iránya véletlenszerű, emiatt az eredeti irányban áthaladó fény intenzitása csökken. A vizsgálandó kolloid oldatunkban ez lesz a meghatározó oka a fény gyengülésének. Ha a közegre oldalról nézünk rá, látjuk is a szórt fényt. A fény hullámhosszához képest kis méretű részecskéken történő szórás esetén azt tapasztaljuk, hogy a hosszú hullámokat kevéssé hatásosan szórják, mint a rövid hullámokat. A probléma matematikai vizsgálatát Rayleigh végezte el elsőként, ezért ezt a típusú szórást Rayleigh-féle fényszórásnak is nevezik. Ez a folyamat felelős az ég kék és a nap sárgás színéért. Ha a szórás a fény hullámhosszánál nagyobb részecskéken történik, akkor Mie-féle szórásról beszélünk. Ebben az esetben a szórt fény intenzitása nem, vagy igen kis mértékben függ csak a hullámhossztól. Emiatt látjuk a felhőket fehér, vagy szürke színűnek. 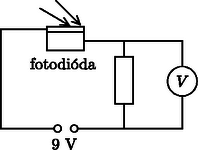Fényintenzitás mérése A fényintenzitást a következő mérőeszközzel mérjük relatív egységekben: A fotodiódára záró irányú feszültséget kapcsolunk, mely a megvilágítás hatására vezetővé válik, ekkor az ellenálláson áram folyik. Voltmérővel mérjük az ellenálláson eső feszültséget.     Mérési feladatok: 1. A zseblámpaizzó segítségével mérje ki a feszültség változását az izzószál és a fotodióda távolságának függvényében! Ábrázolja grafikusan a feszültség‐pozíció függvényt! Alkalmas transzformáció segítségével linearizálja a feszültség‐pozíció függvényt! Állapítsa meg, hogy a feszültség mely tartományában függ lineárisan a fényintenzitástól! (A zseblámpaizzót pontszerű fényforrással közelítjük.) Egyes tartományokban ez a függvény eltérhet a lineáristól. Mi lehet ennek az oka? Tanulmányozza a kolloid oldatban történő fényszórást! Mérje meg az üveghengerbe töltött folyadékon áthaladó lézerfény intenzitását az oldat vastagságának függvényében! Megjegyzések: A fotodióda gondos elhelyezésével elérhető, hogy a fényfolt a fotodióda fényérzékeny részére essen. A lézerből kilépő fényt párhuzamos nyalábnak tekintjük. A belépő és kilépő felületeken fellépő reflexiós veszteségek hatását úgy lehet figyelembe venni, hogy referenciának egy kb. 5 mm-es folyadékoszlopnál mért intenzitást választunk. 2. Ábrázolja grafikonon a mért adatokat! Állapítson meg kvantitatív összefüggést az áthaladó lézerfény intenzitása és az oldat vastagsága között! Adjon meg olyan mennyiséget, amely jellemzi a fény gyengülését! 3. Az egyik asztalon talál néhány edényt, melyekben különböző kolloid oldatok vannak. Mindegyikbe világítson bele a lézerrel és az izzólámpával. Írja le megfigyeléseit! Ezt a feladatot a versenyzők egymás után fogják elvégezni! Az oldatokat vigye a saját asztalához és ott végezzen megfigyeléseket! Ha elkészült a munkával kérjük vigye vissza az oldatokat!!! Az elvégzett méréseiről és a levont következtetésekről készítsen mérési jegyzőkönyvet, mely tartalmazza a mért adatokat, és a mért adatokból a következtetésekig vezető gondolatmenetét!