Kezdőlap


Cím:	A tehetetlenségi nyomatékról
Szerző(k):	Pálfalvi László
Füzet:	2007/január, 38 - 43. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek, Tehetetlenségi nyomaték

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy merev test valamely rögzített tengely körüli forgómozgásának alapegyenlete:

\begin{matrix} M = Θ β, \end{matrix}

ahol

M

a testre ható külső erők forgatónyomatéka az adott tengelyre vonatkoztatva,

β

a test szöggyorsulása,

Θ

pedig a testnek az adott tengelyre vonatkoztatott tehetetlenségi nyomatéka. Látható, hogy

Θ

hasonló szerepet tölt be a forgómozgás leírásánál, mint az

F = m a

mozgásegyenletben a tömeg. Az alábbiakban néhány, a tehetetlenségi nyomatékkal kapcsolatos tételt mutatunk be, és igazoljuk is azokat.
Egy adott tengelytől

r

távolságra lévő

m

tömegű tömegpont tehetetlenségi nyomatéka definíció szerint

\begin{matrix} Θ = m r^{2} . \end{matrix}

((1))

N

darab tömegpontból álló rendszer tehetetlenségi nyomatéka az egyes tömegpontok tehetetlenségi nyomatékainak az összege:

\begin{matrix} Θ = m_{1}^{} r_{1}^{2} + m_{2}^{} r_{2}^{2} + ... + m_{N}^{} r_{N}^{2} = \sum_{i = 1}^{N} m_{i}^{} r_{i}^{2}, \end{matrix}

((2))

ahol

m_{i}

i

-edik tömegpont tömege,

r_{i}

pedig a tengelytől mért távolsága.
A (2) egyenletből következik, hogy több testből álló rendszer tehetetlenségi nyomatéka megegyezik az egyes testek tehetetlenségi nyomatékainak az összegével. Ez az ún. addíciós tétel.
Ugyancsak a (2) összefüggésből következő tulajdonság, hogy egy rendszer tehetetlenségi nyomatéka nem változik, ha annak pontjait a tengellyel párhuzamosan eltoljuk, és akkor sem változik meg a tehetetlenségi nyomaték, ha egy testet a kérdéses tengellyel párhuzamosan összelapítunk vagy megnyújtunk. Ez a megállapítás lapítási tétel néven ismert. Eszerint például egy homogén hengernek, egy lapos korongnak és egy (elméletileg végtelen vékony) körlapnak a körlapjukra merőleges tengelyre vonatkozó tehetetlenségi nyomatéka megegyezik, ha a testek tömege is és a sugara is ugyanakkora (1. ábra).

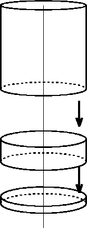1. ábra

Ha egy lapos (síkbelinek tekinthető) test tehetetlenségi nyomatékát vizsgáljuk, érdekes megállapításra juthatunk. Tekintsük a testnek egy tetszőleges pontját! Vegyünk fel egy derékszögű koordináta-rendszert, melynek origója ez a kiválasztott pont,

z

tengelye merőleges a lapos test síkjára, a másik két tengely pedig a 2. ábrán látható módon a síkban fekszik.

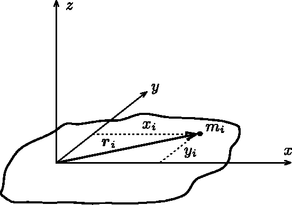2. ábra

z

tengelyre vonatkozó tehetetlenségi nyomaték az ábra jelöléseit és a (2) definíciót használva

\begin{matrix} Θ_{z} = \sum_{i = 1}^{N} m_{i}^{} r_{i}^{2}, \end{matrix}

((3))

és mivel

r_{i}^{2} = x_{i}^{2} + y_{i}^{2}

, fennáll

\begin{matrix} Θ_{z} = \sum_{i = 1}^{N} m_{i}^{} x_{i}^{2} + \sum_{i = 1}^{N} m_{i}^{} y_{i}^{2} . \end{matrix}

((4))

Vegyük észre, hogy (4) jobb oldalának első tagja nem más, mint az

y

tengelyre vonatkozó

Θ_{y} = \sum_{i = 1}^{N} m_{i} x_{i}^{2}

, második tagja pedig az

x

tengelyre vonatkozó

Θ_{x} = \sum_{i = 1}^{N} m_{i} y_{i}^{2}

tehetetlenségi nyomaték, hiszen az összegekben az egyes tömegpontok tömegének és az adott tengelytől mért távolság négyzetének szorzata szerepel. Lapos testekre érvényes tehát a

\begin{matrix} Θ_{z} = Θ_{x} + Θ_{y} \end{matrix}

((5))

összefüggés, azaz egy lapos testnek a lapjára merőleges, egyébként tetszőleges tengelyre vonatkozó tehetetlenségi nyomatéka megegyezik a tengelyt metsző, két egymásra merőleges, a síklapban fekvő tengelyre vonatkozó tehetetlenségi nyomaték összegével. Ezt a tételt poláris-ekvatoriális tételnek hívjuk.
Végül igazoljuk a ‐ KöMaL olvasói közül bizonyára sokaknak ismerős ‐ Steiner-tételt, miszerint a tömegközépponton (TKP) átmenő tengellyel párhuzamos, attól

d

távolságra lévő tengelyre vonatkozó tehetetlenségi nyomaték

\begin{matrix} Θ = Θ^{(TKP)} + m d^{2}, \end{matrix}

ahol

m

a test tömege,

Θ^{(TKP)}

a tömegközépponton átmenő tengelyre vonatkozó tehetetlenségi nyomaték.
Tekintsünk először egy lapos testet! A tömegközépponton és az

A

ponton átmenő tengelyek legyenek merőlegesek a test síkjára (lásd a 3. ábrát!)

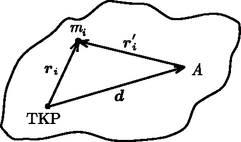3. ábra

A testet kicsiny tömegpontokra bontva az

i

-edik tömegpontba mutató

r_{i}

és

r'_{i}

vektorok közötti kapcsolat

r'_{i} = r_{i} - d

. A tengelyek távolsága

| d | = d

. Az

A

ponton átmenő tengelyre vonatkozó tehetetlenségi nyomaték

\begin{matrix} Θ^{(A)} & = \sum_{i = 1}^{N} m_{i} {r'_{i}}^{2} = \sum_{i = 1}^{N} m_{i} {(r_{i} - d)}^{2} = \sum_{i = 1}^{N} m_{i} {r_{i}}^{2} - 2 d (\sum_{i = 1}^{N} m_{i} r_{i}) + m d^{2} = & (6) \\ = Θ^{(TKP)} + m d^{2}, \end{matrix}

ahol kihasználtuk, hogy a tömegközéppont definíciója szerint

\sum_{i = 1}^{N} m_{i} r_{i} = 0

. Ezzel lapos testre beláttuk a Steiner-tételt.
Vizsgáljunk most egy tetszőleges (tehát nem lapos) merev testet! Osszuk fel a szóban forgó testet

M

darab lapos szeletre olyan síkokkal, amelyek merőlegesek egy ‐ a TKP-n átmenő ‐ tetszőlegesen kiválasztott tengelyre. A 4. ábrán a

J

-edik ilyen szelet látható, jelöljük ennek tömegét

m_{J}

-vel. (A nagybetűs index használata arra utal, hogy itt most nem tömegpontokról, hanem lapos szeletekről beszélünk.)

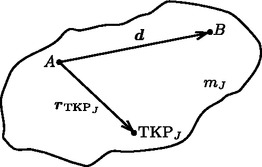4. ábra

A merev test tömegközéppontján átmenő tengely a lapos szelet síkjának

A

pontján, egy vele párhuzamos másik tengely pedig a

B

pontján halad keresztül. A 4. ábrán a vizsgált szelet tömegközéppontját (

{TKP}_{J}

) is feltüntettük. A szelet

A

és

B

pontján, valamint saját tömegközéppontján átmenő tengelyre vonatkozó tehetetlenségi nyomatékának kapcsolata a (6) összefüggés és a 4. ábra alapján:

\begin{matrix} Θ_{J}^{(A)} & = Θ_{J}^{(TKP)} + m_{J} r_{{TKP}_{J}}^{2}, & (7) \\ Θ_{J}^{(B)} & = Θ_{J}^{(TKP)} + m_{J} {(r_{{TKP}_{J}} - d)}^{2} = & (8) \\ = Θ_{J}^{(TKP)} + m_{J} d^{2} - 2 d (m_{J} r_{{TKP}_{J}}) + m_{J} r_{{TKP}_{J}}^{2} . \end{matrix}

A (7) és (8) összefüggésekből

\begin{matrix} Θ_{J}^{(B)} = Θ_{J}^{(A)} + m_{J} d^{2} - 2 d (m_{J} r_{{TKP}_{J}}) \end{matrix}

((9))

adódik. Az addíciós tétel szerint a merev test tömegközéppontján átmenő tengelyre, illetve egy azzal párhuzamos, tőle

d

távolságra levő tengelyre vonatkozó tehetetlenségi nyomatékok közötti összefüggés:

\begin{matrix} Θ^{(B)} = \sum_{J = 1}^{M} Θ_{J}^{(B)} = \sum_{J = 1}^{M} [Θ_{J}^{(A)} + m_{J} d^{2} - 2 d (m_{J} r_{{TKP}_{J}})] = Θ^{(A)} + m d^{2} . \end{matrix}

((10))

(Ismét kihasználtuk, hogy a tömegközéppont definíciója szerint

\sum_{J = 1}^{M} m_{J} r_{{TKP}_{J}} = 0

.) Ezzel a Steiner-tételt általánosan igazoltuk.
Az előző tételek ismerete lehetővé teszi, hogy bizonyos esetekben elemi módszerekkel is meghatározhassuk egy-egy test tehetetlenségi nyomatékát.

1. példa. Határozzuk meg egy

m

tömegű,

L

hosszúságú, homogén tömegeloszlású vékony rúd tehetetlenségi nyomatékát a hossztengelyére merőleges tömegközépponti tengelyre!

Megoldás. Jelöljük a kérdéses tehetetlenségi nyomatékot

Θ_{m, L}

-lel, ahol az index a rúd tömegére és a hosszára utal. Hosszabbítsuk meg gondolatban a vizsgált rudat olymódon, hogy mindkét végéhez egy-egy, az eredetivel megegyező tömegű és hosszúságú rudat erősítünk (5. ábra). Ekkor egy

3 m

tömegű és

3 L

hosszúságú testet kapunk. Ennek tehetetlenségi nyomatéka az addíciós tétel és a Steiner-tétel felhasználásával így számítható:

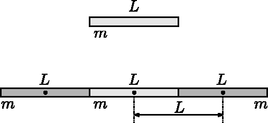\begin{matrix} Θ_{3 m,3 L} = Θ_{m, L} + 2 (Θ_{m, L} + m L^{2}) . \end{matrix}

((11))

5. ábra

Másrészt viszont (2) alapján nyilván igaz, hogy

\begin{matrix} Θ_{3 m,3 L} = 3 \cdot Θ_{m,3 L} és Θ_{m,3 L} = 3^{2} \cdot Θ_{m, L}, \end{matrix}

vagyis

\begin{matrix} Θ_{3 m,3 L} = 27 \cdot Θ_{m, L} . \end{matrix}

((12))

(11) és (12) összevetéséből a vékony rúd tehetetlenségi nyomatékára

\begin{matrix} Θ_{m, L} = \frac{1}{12} m L^{2} \end{matrix}

((13))

adódik.

2. példa. Határozzuk meg egy

m

tömegű,

R

sugarú, homogén tömegeloszlású vékonyfalú gömbhéj (például egy pingponglabda) tehetetlenségi nyomatékát a középpontján átmenő tengelyre! (Felhasználhatjuk, hogy egy homogén, tömör gömb tehetetlenségi nyomatéka

\frac{2}{5} m R^{2} .

)

Megoldás. Jelöljük a gömbhéj vastagságát

h

-val (

h ≪ R

), és számítsuk ki a gömbhéj sűrűségét! Mivel a térfogata

\begin{matrix} V = \frac{4 π}{3} R^{3} - \frac{4 π}{3} {(R - h)}^{3} = 4 π R^{2} h (1 - \frac{h}{R} + \frac{h^{2}}{3 R^{2}}) \approx 4 π R^{2} h, \end{matrix}

a sűrűség jó közelítéssel

\begin{matrix} ϱ = \frac{m}{4 π R^{2} h} . \end{matrix}

((14))

A gömbhéj keresett

Θ

tehetetlenségi nyomatékát az addíciós tétel felhasználásával határozhatjuk meg. A gömbhéj és egy

(R - h)

sugarú tömör gömb együtt egy

R

sugarú tömör gömböt képez, így fennáll

\begin{matrix} Θ + \frac{2}{5} {(R - h)}^{2} \cdot \frac{4 π}{3} {(R - h)}^{3} ϱ = \frac{2}{5} R^{2} \cdot \frac{4 π}{3} R^{3} ϱ, \end{matrix}

ahonnan (14) felhasználásával és algebrai átalakítások után kapjuk:

\begin{matrix} Θ = \frac{8 π}{15} ϱ [R^{5} - {(R - h)}^{5}] \approx \frac{8 π}{15} \cdot \frac{m}{4 π R^{2} h} \cdot 5 R^{4} h = \frac{2}{3} m R^{2} . \end{matrix}

((15))

3. példa. Határozzuk meg egy

m

tömegű,

R

külső és

r

belső sugarú,

L

hosszúságú, homogén tömegeloszlású egyenes cső tehetetlenségi nyomatékát a hossztengelyére merőleges tömegközépponti tengelyre! (Felhasználhatjuk az 1. példa végeredményét, valamint azt, hogy egy homogén, tömör rúd tehetetlenségi nyomatéka a szimmetriatengelyére vonatkoztatva

m R^{2} / 2.

)

Megoldás. Szeleteljük fel a testet a forgástengelyére merőlegesen sok vékony,

Δ z

vastagságú, külön-külön már laposnak tekinthető ,,körgyűrűre''. Egy-egy ilyen darabka tömege

\begin{matrix} Δ m = m \frac{Δ z}{L}, \end{matrix}

((16))

a síkjára merőleges, tömegközépponti tengelyre vonatkozó

Θ_{1}

tehetetlenségi nyomatéka pedig ‐ az addíciós tétel értelmében ‐ egy

R

és egy

r

sugarú tömör korong tehetetlenségi nyomatékának különbségeként áll elő. Mivel a test sűrűsége

\begin{matrix} ϱ = \frac{m}{π L (R^{2} - r^{2})}, \end{matrix}

((17))

a körgyűrű-szelet tehetetlenségi nyomatéka

\begin{matrix} Θ_{1} = \frac{1}{2} (ϱ R^{2} π Δ z) R^{2} - \frac{1}{2} (ϱ r^{2} π Δ z) r^{2} . \end{matrix}

((18))

Ez (16) és (17) felhaszanálásával így is felírható:

\begin{matrix} Θ_{1} = \frac{1}{2} Δ m (R^{2} + r^{2}) . \end{matrix}

((19))

Minket azonban nem ez (a lapos test síkjára merőleges tengelyhez tartozó), hanem a test síkjában fekvő tömegközépponti tengelyre vonatkozó

Θ_{2}

tehetetlenségi nyomaték érdekel. A poláris-ekvatoriális tétel és a forgási szimmetria felhasználásával

Θ_{1} = Θ_{2} + Θ_{2}

, azaz

\begin{matrix} Θ_{2} = \frac{Θ_{1}}{2} = \frac{1}{4} Δ m (R^{2} + r^{2}) . \end{matrix}

((20))

Az egyes körgyűrű-szeletek tehetetlenségi nyomatéka a cső középpontján átmenő (a szeletke síkjától

z

távolságra fekvő) tengelyre vonatkoztatva a Steiner-tétel értelmében

\begin{matrix} Δ Θ = \frac{1}{4} Δ m (R^{2} + r^{2}) + Δ m z^{2} . \end{matrix}

((21))

Az egész cső tehetetlenségi nyomatéka a kérdéses tengelyre az addíciós tétel alkalmazásával kapható meg:

\begin{matrix} Θ = \sum Δ Θ = \sum \frac{1}{4} Δ m (R^{2} + r^{2}) + \sum Δ m z^{2} . \end{matrix}

((22))

A jobb oldal utolsó tagja nem más, mint egy

m

tömegű,

L

hosszúságú rúd tehetetlenségi nyomatéka a rúdra merőleges tömegközépponti tengelyre, ami a (13) összefüggés szerint

\frac{1}{12} m L^{2}

. Végeredményünk tehát:

\begin{matrix} Θ = \frac{1}{4} m (R^{2} + r^{2}) + \frac{1}{12} m L^{2} . \end{matrix}

((23))