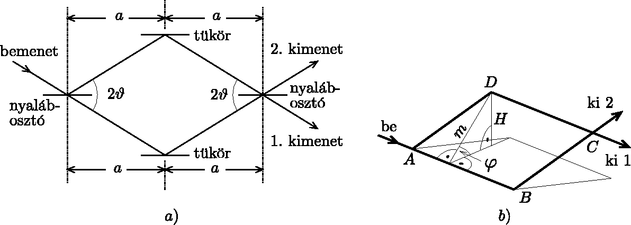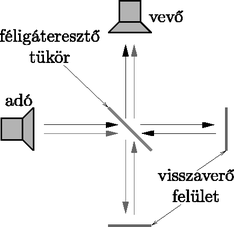Kezdőlap


Cím:	A 37. Nemzetközi Fizikai Diákolimpia feladatai II.
Szerző(k):	Honyek Gyula , Tasnádi Tamás
Füzet:	2006/november, 493 - 504. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az elméleti feladatok megoldása¹

1. feladat. A gravitáció hatása egy neutroninterferométerben

Geometriai elrendezés

1.1. Az 1.a. ábráról leolvasható, hogy az interferáló nyalábok által határolt rombusz átlói

2 a

, illetve

2 a tg ϑ

hosszúságúak, így a keresett terület

A = 2 a^{2} tg ϑ

.
1.2. A

2 ϑ

szögű rombusz magassága

m = \frac{a}{cos ϑ} sin (2 ϑ) = 2 a sin ϑ

, tehát a keresett távolság:

H = m sin φ = 2 a sin ϑ sin φ

(1.b. ábra).

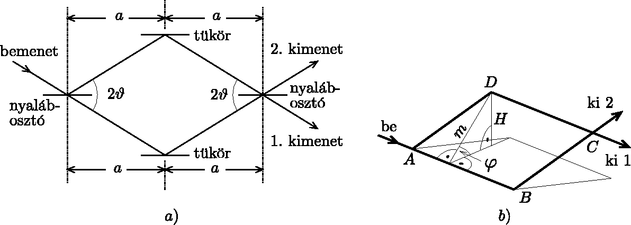1. ábra

Optikai úthossz

1.3. A Föld nehézségi erőterében mozgó neutron gravitációs potenciális energiája növekszik, ha a neutron a vízszinteshez képest magasabb helyre kerül. Ennek következtében mozgási energiája, s vele együtt az impulzusa csökken, a hullámhossza tehát megnő. A feladatban közölt adatok szerint az interferáló neutronok tipikus hullámhossza

λ \approx 10^{- 10} m

nagyságrendű, ez azt jelenti, hogy sebességük

\begin{matrix} v = \frac{h}{λ M} \approx 4 \cdot 10^{3} \frac{m}{s}, \end{matrix}

ami jóval kisebb, mint a fénysebesség, tehát nem kell relativisztikus hatásokkal számolnunk.
Az 1.b. ábráról látható, hogy az

A D

, illetve

B C

ferde szakaszok egymás vízszintes eltoltjai, tehát az optikai úthosszkülönbségbe csak az

L = \frac{a}{cos ϑ}

hosszúságú vízszintes szakaszok adnak járulékot:

\begin{matrix} Δ N_{opt} = \frac{L}{λ_{0}} - \frac{L}{λ_{1}} = \frac{a}{λ_{0} cos ϑ} (1 - \frac{λ_{0}}{λ_{1}}), \end{matrix}

ahol

λ_{0}

, illetve

λ_{1}

A B

, illetve

C D

szakaszon mérhető hullámhosszt jelöli.
A neutronok impulzusa

\frac{h}{λ}

, így az energiamegmaradás törvénye szerint

\begin{matrix} \frac{1}{2 M} {(\frac{h}{λ_{0}})}^{2} = \frac{1}{2 M} {(\frac{h}{λ_{1}})}^{2} + M g H, \end{matrix}

ahonnan

\begin{matrix} \frac{λ_{0}}{λ_{1}} = \sqrt[]{1 - 2 \frac{g M^{2}}{h^{2}} λ_{0}^{2} H} \approx 1 - \frac{g M^{2}}{h^{2}} λ_{0}^{2} H . \end{matrix}

(A legutolsó közelítésnél felhasználtuk, hogy

\frac{g M^{2}}{h^{2}} λ_{0}^{2} H \approx 10^{- 7} ≪ 1

.)
Így az optikai úthosszkülönbségre azt kapjuk, hogy

\begin{matrix} Δ N_{opt} = \frac{a}{λ_{0} cos ϑ} \frac{g M^{2}}{h^{2}} λ_{0}^{2} H = 2 \frac{g M^{2}}{h^{2}} a^{2} λ_{0} tg ϑ sin φ . \end{matrix}

1.4. A fenti eredmény az 1.2. pontban kiszámolt

A

terület és a

V

térfogat segítségével az

\begin{matrix} Δ N_{opt} = \frac{λ_{0} A}{V} sin φ alakban írható, ahol V = 1, 597 \cdot 10^{- 14} m^{3}. \end{matrix}

1.5. Intenzitásmaximum esetén az optikai úthosszak különbsége egész szám,

Δ N_{opt} = 0, \pm 1, \pm 2, ...,

míg intenzitásminimum esetén félegész,

Δ N_{opt} = \pm \frac{1}{2}, \pm \frac{3}{2}, \pm \frac{5}{2}, ...,

így a ciklusok keresett

n

száma:

\begin{matrix} n = Δ N_{opt} |_{ϕ = - 90^{\circ}}^{90^{\circ}} = \frac{2 λ_{0} A}{V} . \end{matrix}

Kísérleti adatok

1.6. A megadott

a = 3, 6 cm

és

ϑ = 22, 1^{\circ}

értékek mellett az interferométer területe

A = 10, 53 cm^{2}

, így a keresett hullámhossz:

\begin{matrix} λ_{0} = \frac{n V}{2 A} = \frac{19 \cdot 1, 597 \cdot 10^{- 14}}{2 \cdot 1, 053 \cdot 10^{- 3}} m = 0, 1441 nm = 1, 441 \cdot 10^{- 10} m. \end{matrix}

1.7. Ugyancsak az 1.5. pontban levezetett képlet alapján

n = 30

és

λ_{0} = 0, 2

nm mellett a terület:

\begin{matrix} A = \frac{n V}{2 λ_{0}} = \frac{30 \cdot 1, 597 \cdot 10^{- 14}}{2 \cdot 2 \cdot 10^{- 10}} m = 11, 98 cm^{2}. \end{matrix}

2. feladat. Mozgó rúd megfigyelése

Alapvető összefüggések

2.1. A lyukkamerával készített képen az

\tilde{x}

helyen látható rúddarabkát kirajzoló fény

T = \frac{\sqrt[]{D^{2} + {\tilde{x}}^{2}}}{c}

idővel korábban indult, mint a felvétel készítésének időpontja. Ennyi idő alatt a rúd

v T

távolságot tesz meg, tehát a felvétel készítésekor a rúd valódi helyzete:

x = \tilde{x} + β \sqrt[]{D^{2} + {\tilde{x}}^{2}}

.
2.2. A fenti egyenletből

\tilde{x}

így fejezhető ki:

\tilde{x} = γ^{2} x - β γ \sqrt[]{D^{2} + {(γ x)}^{2}}

A rúd látszólagos hossza

2.3. A Lorentz-kontrakciónak megfelelően a mozgó rúd hossza

L / γ

, így a mozgó rúd két végének valódi helyzete:

\begin{matrix} x_{\pm} = x_{0} \pm \frac{L}{2 γ}, \end{matrix}

ahol a pozitív jel a rúd elejének, a negatív pedig a végének felel meg.
A lyukkamera képe a rúd két végét a

\begin{matrix} {\tilde{x}}_{\pm} = γ (γ x_{0} \pm \frac{L}{2}) - β γ \sqrt[]{D^{2} + {(γ x_{0} \pm \frac{L}{2})}^{2}} \end{matrix}

helyeken mutatja. Így a rúd

\tilde{L} = {\tilde{x}}_{+} - {\tilde{x}}_{-}

látszólagos hossza

\begin{matrix} \tilde{L} = γ L + β γ \sqrt[]{D^{2} + {(γ x_{0} - \frac{L}{2})}^{2}} - β γ \sqrt[]{D^{2} + {(γ x_{0} + \frac{L}{2})}^{2}} . \end{matrix}

2.4. Mivel a rúd állandó

v

sebességgel mozog, azaz

\frac{d x_{0}}{d t} = v

, így a rúd látszólagos hosszára vonatkozó kérdés azt jelenti, hogy az

\tilde{L}

mennyiség növekszik vagy csökken, ha

x_{0}

növekszik. A rúd látszólagos hosszát mutató kifejezésben szereplő két négyzetgyökös tagot a 2. ábra mutatja vázlatosan.

2. ábra

A ,,

-

''-os és a ,,

+

''-os négyzetgyökös kifejezések különbségéről világosan látszik, hogy ez a különbség folyamatosan csökken, miközben

x_{0}

növekszik. Tehát az

\tilde{L}

látszólagos hossz az idő függvényében folyamatosan csökken.

Szimmetrikus kép

2.5. Szimmetria okokból a rúd látszólagos hossza a szimmetrikus képen megegyezik a rúdnak a lyukkamera koordináta-rendszerében mért ,,valódi'' hosszával, mert a rúd két végéről egyszerre elinduló fény egyszerre ér a lyukkamerába. Ennek megfelelően

\tilde{L} = L / γ

(ami természetesen különbözik a rúd nyugalmi rendszerében észlelt

L

hossztól).
2.6. Ebben az esetben a rúd végpontjainak látszólagos helyzetére érvényes az

{\tilde{x}}_{-} = - {\tilde{x}}_{+}

összefüggés, amit így is kifejezhetünk:

\begin{matrix} 0 = {\tilde{x}}_{+} + {\tilde{x}}_{-} = 2 γ^{2} x_{0} - β γ \sqrt[]{D^{2} + {(γ x_{0} + \frac{L}{2})}^{2}} - β γ \sqrt[]{D^{2} + {(γ x_{0} - \frac{L}{2})}^{2}} . \end{matrix}

Hasonlítsuk össze ezt a kifejezést a szimmetrikus helyzetű rúd hosszával:

\begin{matrix} \frac{L}{γ} = {\tilde{x}}_{+} - {\tilde{x}}_{-} = γ L - β γ \sqrt[]{D^{2} + {(γ x_{0} + \frac{L}{2})}^{2}} + β γ \sqrt[]{D^{2} + {(γ x_{0} - \frac{L}{2})}^{2}} . \end{matrix}

Észrevehetjük, hogy a négyzetgyökös tagok kifejezhetők:

\begin{matrix} \sqrt[]{D^{2} + {(γ x_{0} \pm \frac{L}{2})}^{2}} = \frac{2 γ^{2} x_{0} \pm (γ L - \frac{L}{γ})}{2 β γ} = \frac{γ x_{0}}{β} \pm \frac{β L}{2} . \end{matrix}

Akár a ,,

+

'', akár a ,,

-

'' előjelű változatot választjuk, ugyanarra az eredményre jutunk:

\begin{matrix} x_{0} = β \sqrt[]{D^{2} + {(\frac{L}{2 γ})}^{2}} . \end{matrix}

2.7. A szimmetrikus képen a rúd középpontjának látszólagos helyzetét a 2.2. alkérdésre adott válasz alapján számíthatjuk ki:

\begin{matrix} {\tilde{x}}_{0} = γ^{2} x_{0} - β γ \sqrt[]{D^{2} + {(γ x_{0})}^{2}} = β γ (\sqrt[]{{(γ D)}^{2} + {(\frac{L}{2})}^{2}} - \sqrt[]{{(γ D)}^{2} + {(\frac{β L}{2})}^{2}}) . \end{matrix}

A középpont a rúd elejének képétől

l = {\tilde{x}}_{+} - {\tilde{x}}_{0} = \frac{L}{2 γ} - {\tilde{x}}_{0}

távolságra van, amiből

\begin{matrix} l = \frac{L}{2 γ} - β γ \sqrt[]{{(γ D)}^{2} + {(\frac{L}{2})}^{2}} + β γ \sqrt[]{{(γ D)}^{2} + {(\frac{β L}{2})}^{2}}, \end{matrix}

ami így is felírható:

\begin{matrix} l = \frac{L}{2 γ} (1 - \frac{\frac{β L}{2}}{\sqrt[]{{(γ D)}^{2} + {(\frac{L}{2})}^{2}} + \sqrt[]{{(γ D)}^{2} + {(\frac{β L}{2})}^{2}}}) . \end{matrix}

Nagyon korai és nagyon késői képek

2.8. A nagyon korai képek

x_{0}

nagyon nagy negatív értékeihez tartoznak, így a nagyon korai képeken a rúd látszólagos hossza:

\begin{matrix} {\tilde{L}}_{korai} = \tilde{L} (x_{0} \to - \infty) = (1 + β) γ L = \sqrt[]{\frac{1 + β}{1 - β}} L . \end{matrix}

Ugyanígy a nagyon késői képek

x_{0}

nagyon nagy pozitív értékeihez tartoznak, így a nagyon késői képeken a rúd látszólagos hossza:

\begin{matrix} {\tilde{L}}_{késői} = \tilde{L} (x_{0} \to + \infty) = (1 - β) γ L = \sqrt[]{\frac{1 - β}{1 + β}} L . \end{matrix}

A kifejezésekből következik, hogy

{\tilde{L}}_{korai} > {\tilde{L}}_{késői}

, tehát a 3 méteres látszólagos kép korai, míg az 1 méteres késői kép.

Megjegyzés. Az utolsó három részfeladat a múlt havi számunkból tévedésből kimaradt; ezek kérdéseit most pótoljuk. (A szerk.)

2.9. (1 pont) Határozd meg a rúd

v

sebességét!

Az előző kifejezésekből a

β = \frac{v}{c}

arány kifejezhető:

\begin{matrix} β = \frac{{\tilde{L}}_{korai} - {\tilde{L}}_{késői}}{{\tilde{L}}_{korai} + {\tilde{L}}_{késői}}, \end{matrix}

vagyis

β = \frac{1}{2}

, tehát

v = \frac{c}{2}

.
2.10. (0,6 pont) Határozd meg a nyugvó rúd

L

hosszát!
A sebességarányhoz hasonlóan határozható meg

γ

is:

\begin{matrix} γ = \frac{{\tilde{L}}_{korai} + {\tilde{L}}_{késői}}{2 \sqrt[]{{\tilde{L}}_{korai} \cdot {\tilde{L}}_{késői}}} = \frac{2}{\sqrt[]{3}} = 1, 155. \end{matrix}

Ezzel kifejezhető a nyugvó rúd hossza:

L = \sqrt[]{{\tilde{L}}_{korai} \cdot {\tilde{L}}_{késői}} = 1, 73 m

.
2.11. (0,4 pont) Számold ki a szimmetrikus képen látható rúd látszólagos hosszát!
A 2.5. alkérdésnek megfelelően a rúd látszólagos hossza a szimmetrikus képen:

\begin{matrix} \tilde{L} = \frac{2 {\tilde{L}}_{korai} \cdot {\tilde{L}}_{késői}}{{\tilde{L}}_{korai} + {\tilde{L}}_{késői}} = 1, 5 m. \end{matrix}

3. feladat.

Digitális kamera

3.1. A digitális kamerák felbontóképességét két tényező korlátozza: a nyílás fényszórása (diffrakciója) és a pixelek mérete. A diffrakció miatti

Θ_{R}

szögfelbontást a fény

λ

hullámhosszának és a kameranyílás átmérőjének aránya határozza meg:

\begin{matrix} Θ_{R} = 1, 22 \frac{λ}{D}, \end{matrix}

ahol az 1,22-es tényező a kameranyílás kör alakjának a következménye. Mivel a legtöbb gyakorlati esetben a tárgy eléggé messze van a kamerától, így a kép a kamera fókuszsíkjában keletkezik, tehát akkor különböztethetünk meg egymástól két képpontot, ha a közöttük lévő távolság nagyobb, mint

\begin{matrix} Δ x = f \cdot Θ_{R} = 1, 22 \cdot λ \cdot F #, \end{matrix}

melynek számszerű értéke:

Δ x = 1, 22 μm

. Becsléskor a lehető legnagyobb nyílást (tehát a lehető legkisebb, vagyis

F # = 2

-es numerikus apertúra értéket) választottuk, valamint a megadott

λ = 500 nm

-es tipikus hullámhosszat használtuk.
3.2. A digitális felbontóképességet a szomszédos pixelek középpontja közötti

l

távolság adja meg. Az 5 Mpix-es kameránk esetén ez a távolság közelítőleg:

\begin{matrix} l = \frac{L}{\sqrt[]{N_{p}}} = 15, 65 μ m. \end{matrix}

Ideális esetben az optikai és a digitális felbontóképesség összhangban van egymással. Ha a sokkal jobb optikai felbontóképességet várjuk el a digitális felbontástól is, akkor a szükséges pixelszám:

\begin{matrix} N = {(\frac{L}{Δ x})}^{2} \approx 823 Mpix. \end{matrix}

3.3. Az optika akkor nem befolyásolja a felbontóképességet, ha

l \geq Δ x

. Ehhez olyan

F # \leq F_{0}

értéket kell választanunk, ahol

\begin{matrix} F_{0} = \frac{L}{1, 22 \cdot λ \cdot \sqrt[]{N_{0}}} = 2 \sqrt[]{\frac{N}{N_{0}}} = 14, 34. \end{matrix}

Mivel a kamerákon ilyen

F #

érték beállítása nem lehetséges, ezért azt a hozzá legközelebbi numerikus apertúrát kell választanunk, ami jobb felbontóképességet ad, vagyis

F_{0} = 11

.
3.4. Ha a szemünktől

z

távolságra lévő képet nézzük, két szomszédos képpont közötti (kicsiny) látószög így adható meg:

φ = \frac{l}{z}

, ahol

l

a szomszédos képpontok közötti távolság. Mivel az emberi szem szög szerinti felbontóképessége kb.

2'

(azaz 2 szögperc²), a kérdéses távolság:

\begin{matrix} z = \frac{l}{φ} = \frac{2, 54 \cdot 10^{- 2} m}{2 \cdot 2, 91 \cdot 10^{- 4} \cdot 300} = 14, 55 cm \approx 15 cm. \end{matrix}

Keménytojás

3.5. Az egész tojásnak el kell érnie a kicsapódási hőmérsékletet. Ez azt jelenti, hogy a tojás hőmérsékletének növekedése:

\begin{matrix} Δ T = T_{c} - T_{0} = 65^{\circ} C - 4^{\circ} C = 61^{\circ} C . \end{matrix}

Így a tojás teljes kicsapódásához szükséges minimális energia:

U = μ V c Δ T

, ahol

V = 4 π R^{3} / 3

a tojás térfogata. A kicsapódáshoz szükséges minimális energia számértéke:

\begin{matrix} U = μ \frac{4 π R^{3}}{3} c (T_{c} - T_{0}) = 16 800 J. \end{matrix}

3.6. Durva becslésként felhasználhatjuk a hővezetés egyszerűsített Fourier-törvényét, és így közelítőleg kiszámíthatjuk a kezdeti

J

hőáramsűrűséget. Feltehetjük, hogy a tojás közepében a hőmérséklet megegyezik a tojás kezdeti

T_{0} = 4^{\circ} C

-os hőmérsékletével, továbbá a tojást jellemző tipikus hossz

Δ r = R

a tojás sugara, illetve az ennek megfelelő hőmérsékletkülönbség

Δ T = T_{1} - T_{0}

, ahol

T_{1} = 100^{\circ} C

a víz forráspontja. Így

\begin{matrix} J = \frac{κ (T_{1} - T_{0})}{R} = 2460 W\cdotm^{- 2}. \end{matrix}

3.7. A fenti hőáram segítségével becslést adhatunk a forró vízből a tojás felszínén át a tojásba áramló hőteljesítmény nagyságára:

\begin{matrix} P = 4 π R^{2} J = 4 π κ R (T_{1} - T_{0}) \approx 19 W. \end{matrix}

3.8. A hőteljesítmény megadja a tojásba behatoló hő mennyiségét másodpercenként. Ezzel és a kicsapódáshoz szükséges energiával közelítő becslést adhatunk a keménytojás

τ

főzési idejére:

\begin{matrix} τ = \frac{U}{P} = \frac{μ c R^{2}}{3 κ} \cdot \frac{T_{c} - T_{0}}{T_{1} - T_{0}} \approx 880 s \approx 15 perc . \end{matrix}

Villámlás

3.9. A villám

Q

töltését az áramerősség-idő függvény görbe alatti területe (esetünkben egy háromszög területe) adja meg:

\begin{matrix} Q = \frac{I_{0} τ}{2} = 5 C. \end{matrix}

3.10. Az átlagos áram a töltés és az idő hányadosa, a lineáris áramerősség-idő függvény miatt egyszerűen a maximális áramérték fele:

\begin{matrix} I = \frac{Q}{τ} = \frac{I_{{max}_{}^{}}}{2} = 50 kA. \end{matrix}

3.11. Mivel a felhő alja negatív töltésű, így a talaj pozitív töltésű, ezért a villámláskor megvalósuló helyzetet lényegében egy gigantikus síkkondenzátorral közelíthetjük. Így a villámcsapás előtti pillanatban a felhalmozódott energia

Q E_{0} h / 2 = 7, 5 \cdot 10^{8} J

, ahol

E_{0} h

a felhő alja és a talaj közötti feszültség. Villámláskor közelítőleg ekkora, 750 MJ-nyi energia szabadul fel. Ezek után már könnyen kiszámíthatjuk, hogy a Föld egy évi összes villámjának energiája, amit (gondolatban) szétosztunk a Föld teljes népessége között, mennyi ideig tudna emberenként egy-egy 100 W-os izzólámpát működtetni:

\begin{matrix} t = \frac{32 \cdot 10^{6}}{6, 5 \cdot 10^{9}} \cdot \frac{7, 5 \cdot 10^{8} J}{100 W} \approx 10 h. \end{matrix}

Hajszálerek

3.12. A Poisseuille-féle törvényt átrendezve megkaphatjuk az összes hajszálér által képviselt

R_{Σ}

eredő áramlási ellenállást:

\begin{matrix} R_{Σ} = \frac{Δ p}{D} = 10^{7} \frac{P a s}{m^{3}}. \end{matrix}

Minthogy a hajszálerek ,,párhuzamosan vannak kapcsolva'', az elektromos analógiát használva

\begin{matrix} \frac{1}{R_{Σ}} = \frac{N}{R}, ahol R = \frac{8 η L}{π r^{4}} \approx 4, 5 \cdot 10^{16} \frac{k g}{m^{4} s} \end{matrix}

egyetlen hajszálér áramlási ellenállása. Innen a hajszálerek száma:

\begin{matrix} N = \frac{R}{R_{Σ}} \approx 4, 5 \cdot 10^{9} . \end{matrix}

3.13. A térfogati ,,vérhozamot'' (

D

) kifejezhetjük a vér

v

áramlási sebességével, valamint az erek

r^{2} π

keresztmetszetével:

\begin{matrix} D = v N r^{2} π, ahonnan v = \frac{D}{N r^{2} π} = 0, 44 \frac{m m}{s}. \end{matrix}

Felhőkarcoló

3.14. A

p V = N k T

ideális gázegyenletnek és az adiabatikus folyamatokat jellemző

p V^{γ} = állandó

összefüggésnek a kombinálásából adódik, hogy adiabatikus folyamat esetén

p^{γ - 1} = K T^{γ}

, ahol

K

a gázra jellemző konstans. Ha a nyomás kis

d p

-vel megváltozik, akkor az egyenlet bal oldala

(γ - 1) p^{γ - 2} d p

-vel változik meg, és hasonlóan kis

d T

hőmérsékletváltozás esetén a jobb oldal

K γ T^{γ - 1} d T

-vel változik meg. E két változás azonban megegyezik, tehát

\begin{matrix} (γ - 1) p^{γ - 2} d p = K γ T^{γ - 1} d T . \end{matrix}

A fenti két egyenletet elosztva egymással megkapjuk a keresett összefüggést:

\begin{matrix} \frac{d T}{T} = (1 - \frac{1}{γ}) \frac{d p}{p} = \frac{2}{7} \frac{d p}{p} . \end{matrix}

Ugyanezt az eredményt úgy is megkaphatjuk, hogy képezzük a

p V = N k T

egyenlet mindkét oldalának kicsiny megváltozását:

p d V + V d p = N k d T

, valamint felírjuk az adiabatikus állapotváltozásra vonatkozó

\begin{matrix} d E + p d V = \frac{5}{2} N k d T + p d V = 0 \end{matrix}

egyenletet (kihasználva, hogy a nitrogénmolekulák szabadsági foka 5). A fenti három egyenletből

V

és

d V

kiküszöbölése után

\begin{matrix} \frac{d T}{T} = \frac{2}{7} \frac{d p}{p} . \end{matrix}

adódik.
3.15. Az

A

vízszintes felületű,

z

magasságban levő,

d z

vastagságú levegőrétegre ható nehézségi erővel a felső és alsó lapra ható nyomás különbségéből származó erő tart egyensúlyt. Az

A d z

térfogatban levő részecskék száma a gáztörvény alapján

N = \frac{p A d z}{k T}

, tehát a gázra ható nehézségi erő

N m g = \frac{p A d z}{k T} m g

, ahol

m

egyetlen részecske tömege. A

d p = p (z + d z) - p (z)

nyomáskülönbségből származó erő pedig

A d p

, tehát

\begin{matrix} \frac{p A d z}{k T} m g = - A d p, ahonnan d p = - \frac{m g p}{k T} d z . \end{matrix}

(A negatív előjel arra utal, hogy a nyomás a magasság növekedésével csökken.)
3.16. Az előző két pontban levezetett összefüggések alapján a hőmérsékletváltozás és a magasságváltozás között a kapcsolat:

\begin{matrix} d T = - (1 - \frac{1}{γ}) \frac{m g}{k} d z = - \frac{2 m g}{7 k} d z . \end{matrix}

Látható, hogy a hőmérséklet a magassággal egyenes arányban csökken, így a keresett hőmérsékletet:

\begin{matrix} T_{fent} = T_{lent} - \frac{2 m g H}{7 k} = 20, 6^{\circ} C. \end{matrix}

(Felhasználtuk, hogy

T_{lent} = 30^{\circ} C

, és

H = 1000

m.)

A mérési feladat³

A versenyzőknek négy különböző hullámtani jelenséget kellett vizsgálni mikrohullámok segítségével. Minden versenyző kapott egy-egy mikrohullámú adó- és vevőkészüléket, árammérő műszert, melyet a vevő egységhez csatlakoztatva a hullám amplitudóját lehetett mérni, szög- és távolságmérő eszközöket, valamint egyszerű ,,optikai'' berendezéseket.
A mikrohullámú sugárzás tartományában működő optikai eszközök első ránézésre igen furcsák. A lencsék, plánparalel lemezek, nyalábosztók, prizmák a normál fényt át nem eresztő műanyagból, illetve viaszból készültek. Az interferencia tanulmányozására használt ,,vékonyréteg'' néhány centiméteres vastagságú hasáb volt, és a Bragg-reflexió vizsgálatához a versenyzők mintegy 20 cm oldalélű fekete dobozt kaptak, melyben egymástól 4‐5 cm távolságban elhelyezett fémrudak alkották a rácsot. E szokatlan méreteket könnyen megértetjük, ha figyelembe vesszük, hogy a mérésben használt mikrohullámú sugárzás hullámhossza körülbelül 3 cm volt.
A mérési feladatok között voltak olyanok is, melyben a versenyzőknek a diákolimpia követelményrendszerében nem szereplő hullámoptikai jelenséget kellett tanulmányozniuk. Ilyenkor ‐ a diákolompiák szellemének megfelelően ‐ a kiadott feladat szövege röviden ismertette a vizsgálandó jelenség leírását, és ezután következett maga a mérés.
Az alábbiakban (érdektelen technikai részletek elhagyásával) rövidítve ismertetjük az olimpián szereplő mérési feladat szövegét, és vázlatosan utalunk a megoldás ,,kényesebb'' részleteire.

1. Michelson-interferométer

A Michelson-féle interferométerben egy nyalábosztó (féligáteresztő tükör) a bemenő elektromágneses hullámot két részre bontja, melyek két különböző utat futnak be, majd visszaverődések után a nyalábosztó ismét egyesíti őket, így szuperponálódnak és interferencia-mintázatot hoznak létre. A 3. ábra a Michelson-interferométer felépítését mutatja. A beérkező hullám két különböző úton jut el a forrástól a vevőkészülékbe. Ez a két hullám szuperponálódik és interferál egymással. Az észlelt jel erőssége a két hullám közötti fáziskülönbségtől függ, ami az optikai úthosszkülönbség változtatásával befolyásolható.

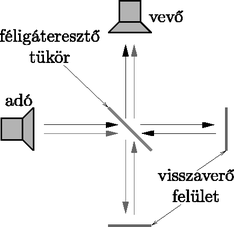3. ábra. A Michelson-interferométer felépítése

A versenyzőknek a rendelkezésre álló eszközökből össze kellett állítaniuk a Michelson-féle interferométert, és az egyik kar hosszának változtatásával meg kellett mérniük a mikrohullám hullámhosszát néhány tizedmilliméter pontossággal.
Könnyű rájönni, hogy az egyik kar hosszát folyamatosan növelve félhullámhosszonként kapunk újra és újra erősítést (illetve gyengítést) a vevőben. Mivel a hullámhosszat viszonylag nagy pontossággal kell meghatározni, ezért célszerű több (körülbelül 10‐20) egymás utáni erősítéshez (vagy gyengítéshez) tartozó úthossznövekedést mérni.

2. ,,Vékonyréteg''-interferencia

Szigetelő anyagból készült ,,vékony'' rétegre eső elektromágneses hullám két nyalábra bomlik (4. ábra). Az

A

nyaláb a réteg felső lapjáról verődik vissza, míg a

B

nyaláb a réteg alsó lapjáról verődik vissza. Az

A

és

B

nyaláb szuperpozíciója adja az úgynevezett vékonyréteg-interferenciát.

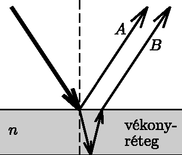4. ábra. Interferencia vékonyrétegen

A

és a

B

nyalábhoz tartozó optikai úthosszak közti különbség erősítő vagy gyengítő interferenciához vezet. Az eredő intenzitás a két interferáló sugár közti útkülönbségtől függ, amit pedig a beesési szög, a sugárzás hullámhossza valamint a (,,vékony-'') réteg vastagsága és

n

törésmutatója határoz meg.
A versenyzőknek fel kellett venni a beesési szög függvényében az eredő intenzitást, majd a kapott grafikon alapján meghatározhatták a vékonyréteg anyagának

n

törésmutatóját és a törésmutató

Δ n

hibáját. A mérés kivitelezésénél többek között arra kellett figyelni, hogy vékonyréteg minden esetben a beeső és a (detektor által meghatározott irányú) visszavert sugarak szögfelezőjére merőlegesen álljon.

3. Megzavart teljes visszaverődés

A teljes visszaverődés jelensége akkor jöhet létre, ha a hullám optikailag sűrűbb közegből optikailag ritkább közeg felé halad. A valóságban (a geometriai optika által jósolt felületi visszaverődés helyett) a beeső hullám valamennyire behatol a kevésbé sűrű közegbe, valamekkora távolságig a felülettel párhuzamosan halad, majd visszatér a sűrűbb közegbe. Ez az effektus a visszaverődő nyaláb

D

eltolódásával írható le, ami a szakirodalomban Goos‐Hänchen-eltolódásként ismert.
Ha két, azonos (

n_{1}

törésmutatójú) anyagból készült testet úgy helyezünk el egymás közelében, hogy a közöttük levő vékony,

d

szélességű térrészt kisebb (

n_{2}

törésmutatójú) közeg (pl. levegő) töltse ki (5. ábra), akkor az elektromágneses hullám mintegy ,,átalagutazik'' a közbülső (második) közegen keresztül. Ezt a meglepő jelenséget megzavart teljes visszaverődésnek hívják. Az áthaladó hullám

I_{t}

intenzitása exponenciálisan csökken a

d

távolság növekedtével:

\begin{matrix} I_{t} = I_{0} e^{- 2 γ d}, ahol γ = \frac{2 π}{λ} \sqrt[]{\frac{n_{1}^{2}}{n_{2}^{2}} sin^{2} α - 1}, \end{matrix}

I_{0}

a beeső hullám intenzitása,

λ

a hullámhossza a

2

-es közegben, és

α

a beesési szög.

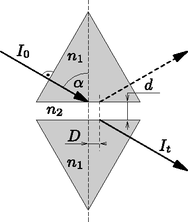5. ábra. Megzavart teljes visszaverődés

A versenyzőknek össze kellett állítani a megzavart teljes visszaverődés tanulmányozására alkalmas mérési elrendezést, majd fel kellett venniük az

I_{t} - d

grafikont, és a mérési adatok elemzésével meghatározhatták a prizmák anyagának

n_{1}

törésmutatóját és annak mérési hibáját.

4. Mikrohullámok elhajlása fémrudakból álló rácson és a Bragg-egyenlet

A kristályok rácsszerkezete a Bragg-egyenlet segítségével vizsgálható:

\begin{matrix} 2 d sin ϑ = m λ, \end{matrix}

ahol

d

jelöli a röntgensugárzást ,,visszaverő'' párhuzamos kristálysíkok közti távolságot,

m

az elhajlás rendje és

ϑ

a beeső röntgensugár és a kristálysíkok közötti szög. A Bragg-egyenlet teljesülése esetén szokás a röntgendiffrakcióban Bragg-reflexióról beszélni.
Mivel a röntgensugarak hullámhossza összemérhető a kristályok rácsállandójával, a hagyományos Bragg-elhajlásos méréseket röntgensugarakkal végzik. Mikrohullámok esetén azonban az elhajlás sokkal nagyobb rácsállandóval rendelkező periodikus szerkezeteken jön létre, ezek akár egy vonalzóval is jól mérhetőek.
Talán ez a feladat volt a mérés legérdekesebb része. A versenyzők egy körülbelül 20 cm oldalélű ,,fekete dobozt'' kaptak, melynek belsejében fémrudakból kialakított kétdimenziós négyzetrácsot helyeztek el (6. ábra). Ennek a rácsnak az átlós síkján kellett vizsgálni a mikrohullámú sugárzás Bragg-reflexióját, ebből lehetett meghatározni az

a

rácsállandót (és annak hibáját). A fekete dobozon csak az átlós irányt jelölték be, maguknak a fémrudaknak a helyzetét természetesen nem láthatták a versenyzők.

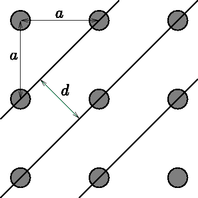6. ábra. A fekete dobozban levő szabályos négyzetrács felülnézetből

¹A feladatok szövegét múlt havi számunkban közöltük.

²Múlt havi számunkban szögperc helyett tévesen szögmásodperc szerepelt.

³A mérés elvégzésére és kiértékelésére 5 óra állt rendelkezésre.