Kezdőlap


Cím:	A 37. Nemzetközi Fizikai Diákolimpia elméleti feladatai
Füzet:	2006/október, 427 - 432. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. A gravitáció hatása egy neutroninterferométerben

Elvi áttekintés. Collela, Overhauser és Werner híres neutroninterferencia kísérletének egy olyan idealizált változatát vizsgáljuk, ahol a tükrökről és a nyalábosztókról feltételezzük, hogy tökéletesek. A kísérletben a gravitációnak a neutronok de Broglie-féle hullámtermészetére kifejtett hatását vizsgálták.

Fizikai elrendezés. Az interferométer elvi felépítése megegyezik a hasonló optikai interferométerek felépítésével, ami az 1.a. ábrán látható. A neutronok az IN bemeneten át lépnek be az interferométerbe, majd az ábrán látható két utat követik. A neutronokat az OUT1 és OUT2 kimenetek egyikén detektáljuk. A két út rombusz alakú területet zár be, amelynek tipikus mérete néhány

cm^{2}

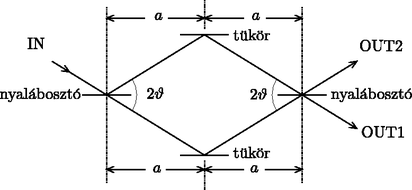1.a. ábra

A neutronok de Broglie-hullámai (tipikus hullámhosszuk

10^{- 10}

m) úgy interferálnak, hogy amikor az interferométer síkja vízszintes, akkor az összes neutron az OUT1 kimeneten lép ki. Azonban, ha az interferométert

φ

szöggel megdöntjük a bejövő neutronok által alkotott tengely körül (lásd az 1.b. ábrát), akkor a megfigyelő a

φ

szögtől függő módon a neutronok másféle eloszlását észleli az OUT1 és OUT2 kimeneteken.

1.b. ábra

Geometriai elrendezés.

φ = 0

esetén az interferométer síkja vízszintes;

φ = 90^{\circ}

esetén a sík függőleges, és a kimenetek a forgástengely felett helyezkednek el.
1.1. (1 pont) Mekkora a rombusz alakú terület

A

nagysága, amit az interferométerben haladó két út határol?
1.2. (1 pont) Mekkora az OUT1 kimenet

H

magassága a forgástengelyen átfektetett vízszintes sík felett?
Fejezd ki

A

-t és

H

-t a következő mennyiségekkel:

a

ϑ

és

φ

Optikai úthossz. Az optikai úthossz megadható egyszerűen egy számmal is, amit jelöljünk

N_{opt}

-tal. Ezt a számot a geometriai úthossz (távolság) és a

λ

hullámhossz hányadosaként definiáljuk. Ha a

λ

hullámhossz változik az optikai út mentén, akkor az

N_{opt}

számot úgy kaphatjuk meg, ha a

λ^{- 1}

függvényt integráljuk az út mentén.
1.3. (3 pont) Mekkora a két út optikai úthosszának

Δ N_{opt}

különbsége, ha az interferométert

φ

szöggel elfordítjuk? Fejezd ki válaszodat a következő mennyiségekkel:

a

ϑ

és

φ

, valamint a neutron

M

tömegével, a bejövő neutronok

λ_{0}

de Broglie-hullámhosszával, a

g

gravitációs gyorsulással és a

h

Planck-állandóval.
1.4. (1 pont) Vezesd be a következő térfogati paramétert:

\begin{matrix} V = \frac{h^{2}}{g M^{2}}, \end{matrix}

és fejezd ki a

Δ N_{opt}

különbséget kizárólag

A

V

λ_{0}

és

φ

segítségével! Állapítsd meg a

V

térfogat számszerű értékét, felhasználva, hogy

M = 1, 675 \cdot 10^{- 27}

kg,

g = 9, 800 m/s^{2}

és

h = 6, 626 \cdot 10^{- 34}

Js.
1.5. (2 pont) Hány ciklus (periódus) észlelhető az OUT1 kimenetnél, ha

φ

értéke

φ = - 90^{\circ}

-tól

φ = 90^{\circ}

-ig növekszik? Egy ciklust úgy értelmezünk, hogy a kimenetnél az intenzitás nagy intenzitásról kicsire csökken, majd visszanő nagyra.

Kísérleti adatok. Egy bizonyos kísérletben az interferométerre jellemző méret:

a = 3, 600

cm, továbbá

ϑ = 22, 10^{\circ}

és 19,00 teljes ciklus észlelhető.
1.6. (1 pont) Számszerűleg mekkora volt

λ_{0}

ebben a kísérletben?
1.7. (1 pont) Ha egy másik, hasonló kísérletben

λ_{0} = 0, 2000

nm hullámhosszúságú neutronokat használnánk, és így 30,00 teljes ciklust észlelnénk, milyen nagy lenne az

A

terület?
Segítség: Ha

| x | ≪ 1

, akkor megengedhető, hogy

{(1 + x)}^{α}

helyett az

1 + α x

közelítést használjuk.

2. feladat. Mozgó rúd megfigyelése
Fizikai elrendezés. Egy lyukkamerával (camera obscura), melynek nyílása

x = 0

-nál, az

x

tengelytől

D

távolságra helyezkedik el, képeket készítünk egy mozgó rúdról, olymódon, hogy a kamera nyílását nagyon rövid időre kinyitjuk. Az

x

tengely mentén egyenlő közű osztások találhatók, ahogy a 2. ábra is mutatja, melyek segítségével a rúd látszólagos hossza leolvasható a kamerával készített képről. A nyugvó rúdról készített egyik képen ez a hossz

L

. A feladatban megfigyelt rúd azonban nincs nyugalomban, hanem állandó

υ

sebességgel mozog az

x

tengely mentén.

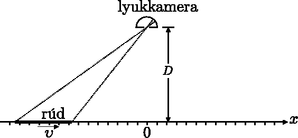2. ábra

Alapvető összefüggések. A lyukkamerával készített képek egyikén a rúd egy rövid darabkája az

\tilde{x}

helyen látható.
2.1 (0,6 pont) Határozd meg a rúd ugyanezen darabkájának valódi

x

helyzetét abban az időpillanatban, amikor a kép készült! Eredményedet az

\tilde{x}

D

L

υ

mennyiségek és a

c = 3, 00 \cdot 10^{8} m/s

fénysebesség segítségével fejezd ki, valamint használd a

\begin{matrix} β = \frac{υ}{c} és γ = \frac{1}{\sqrt[]{1 - β^{2}}} \end{matrix}

jelöléseket, ha ezekkel egyszerűbb alakban adható meg az eredmény.
2.2. (0,9 pont) Határozd meg a fenti kifejezés inverzét is, azaz add meg

\tilde{x}

-t az

x

D

L

υ

és

c

mennyiségek segítségével!
Megjegyzés: A rúd valódi helyzetét abban a vonatkoztatási rendszerben határozzuk meg, amelyben a lyukkamera nyugalomban van.

A rúd látszólagos hossza. A lyukkamerával abban a pillanatban készítünk képet a rúdról, amikor a rúd középpontjának valódi helyzete

x_{0}

.
2.3. (1,5 pont) Az adott mennyiségek segítségével határozd meg a rúd látszólagos hosszát ezen a képen!
2.4. (1,5 pont) Az alábbi lehetőségek egyikének kiválasztásával jelezd, hogyan változik a rúd látszólagos hossza az idő függvényében! A látszólagos hossz

•

először növekszik, elér egy maximális értéket, majd csökken;

•

először csökken, elér egy minimális értéket, majd növekszik;

•

az egész idő alatt csökken;

•

az egész idő alatt növekszik.

Szimmetrikus kép. A lyukkamerával készített képek egyikén a rúd mindkét vége ugyanolyan távolságra látszik a középponttól (origótól).
2.5. (0,8 pont) Határozd meg a rúd látszólagos hosszát ezen a képen!
2.6. (1 pont) Add meg a rúd középpontjának valódi helyzetét abban az időpillanatban, amikor ez a kép készült!
2.7. (1,2 pont) Hol látható a rúd középpontjának képe a felvételen?

Nagyon korai és nagyon késői képek. A lyukkamérával készítettünk egy nagyon korai képet, amikor a kamerához közeledő rúd még igen távol volt, valamint egy nagyon késői képet, amikor a kamerától távolodó rúd már igen messze volt. Az egyik képen a rúd látszólagos hossza 1,00 m, míg a másikon 3,00 m.
2.8. (0,5 pont) Az alábbi lehetőségek egyikének kiválasztásával jelezd, hogy melyik hossz melyik képen látható!

•

A látszólagos hossz 1 m a korai képen, és 3 m a késői képen.

•

A látszólagos hossz 3 m a korai képen, és 1 m a késői képen.

3. feladat. Ez a feladat öt, egymástól független részből áll. Minden részben csak nagyságrendi becslést kell végezned, nem szükséges pontos választ adnod.

Digitális kamera. Tekintsünk egy

N_{p} = 5

Mpix (1

Mpix = 10^{6}

pixel) érzékelőfelületű digitális kamerát. A négyzet alakú, CCD érzékelőlap lineáris mérete (oldala)

L = 35

mm. A kamera lencséjének fókusztávolsága:

f = 38

mm. A lencsén megjelenő, jól ismert számsorozatot (2, 2,8, 4, 5,6, 8, 11, 16, 22)

F

-számoknak (numerikus apertúrának) hívjuk, és így jelölünk:

F #

, és a fókusztávolság és a

D

lencsenyílás (apertúra) átmérőjének arányaként definiálunk:

F # = f / D

.
3.1. (1 pont) Add meg a kamera lehető legjobb, csak a lencse által korlátozott

Δ x_{{min}_{}^{}}

felbontóképességét az érzékelőfelületén. Eredményedet fejezd ki a

λ

hullámhossz és

F #

(numerikus apertúra) segítségével, majd add meg a felbontóképesség számszerű értékét is

λ = 500

nm esetén.
3.2. (0,5 pont) Add meg a megapixelek ahhoz szükséges

N

számát, hogy a CCD érzékelő megfeleljen a fenti optimális felbontóképességnek.
3.3. (0,5 pont) Időnként a fényképészek úgy próbálják a kamerájukat használni, hogy a lehető legkisebb nyílást (apertúrát) állítják be. Tegyük fel, hogy a fényképezőgépünk

N_{0} = 16

Mpix-es, és érzékelőfelületének mérete, valamint lencséjének fókusztávolsága az előzőekkel megegyező. Milyen

F #

értéket állítsunk be, hogy a kép minőségét az optika ne korlátozza?
3.4. (0,5 pont) Tudjuk, hogy az emberi szem szög szerinti felbontóképessége nagyjából

φ = 2''

(szögmásodperc), és egy tipikus nyomtató minimum 300 dpi (dots per inch, azaz pont/hüvelyk) finomsággal nyomtat, legalább milyen minimális

z

távolságra tartsuk az oldalt a szemünktől, hogy ne lássuk külön-külön a pontokat?
Adatok: 1

hüvelyk = 25, 4

mm,

1'' = 2, 91 \cdot 10^{- 4}

rad.

Keménytojás. A hűtőszekrényből kivett tojás hőmérséklete

T_{0} = 4^{\circ} C

. Ezt a tojást forrásban lévő vízbe tesszük. A víz jól ismert forráspontját jelöljük így:

T_{1}

.
3.5. (0,5 pont) Mekkora

U

mennyiségű energiára van szükség ahhoz, hogy az egész tojás kicsapódjon (koagulálódjon)?
3.6. (0,5 pont) Mekkora

J

hőáramsűrűség folyik a tojásba, ha a közepe még hideg?
3.7. (0,5 pont) Mekkora

P

fűtőteljesítmény melegíti ilyenkor a tojást?
3.8. (0,5 pont) Ilyen hőátadással mennyi idő alatt lesz kemény a tojás?
Segítség: Használhatod a hővezetés egyszerűsített Fourier-törvényét:

J = κ Δ T / Δ r

, ahol

Δ T

a feladat tipikus

Δ r

hosszméretéhez tartozó hőmérsékletkülönbség. A

J

hőáramsűrűség mértékegysége:

Wm^{- 2}

.
Adatok: A tojás (tömeg) sűrűsége:

μ = 10^{3} kgm^{- 3}

. A tojás fajhője:

c = 4, 2 JK^{- 1}g^{- 1}

. A tojás sugara:

R = 2, 5

cm. A tojásfehérje kicsapódási hőmérséklete:

T_{c} = 65^{\circ} C

. Hővezetési együttható (melyről feltételezhetjük, hogy a folyékony és a szilárd tojásfehérjére ugyanakkora):

κ = 0, 64 WK^{- 1}m^{- 1}

.
Villámlás. A villámok nagyon leegyszerűsített modelljével foglalkozunk. A villámokat a felhőkben felhalmozódó elektrosztatikus töltések okozzák. A felhők alja rendszerint pozitív töltésű, a tetejük negatív töltésű, és a felhő alatt a talaj negatívan töltött. Ha az elektromos térerősség eléri a levegő átütési értékét, akkor kisülés következik be; ez a villám.

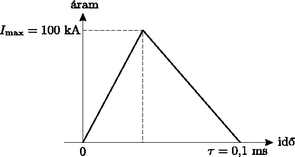3. ábra. Egy villám idealizált impulzusa (a felhő és a talaj között folyó áramerősség az idő függvényében)

A következő kérdésekre ennek az egyszerűsített áramerősség‐idő görbének (3. ábra) és az alábbi adatoknak a segítségével válaszolj:
A felhő alja és a talaj közötti távolság:

h = 1

km.
A nedves levegő átütési térerőssége:

E_{0} = 300 kVm^{- 1}

.
A Földet évente elérő villámok teljes száma:

32 \cdot 10^{6}

.
A Föld népessége:

6, 5 \cdot 10^{9}

ember (= 6,5 Gigaember).
3.9. (0,5 pont) Mekkora egy villám

Q

töltése?
3.10. (0,5 pont) Mekkora átlagos

I

áram folyik villámláskor a felhő alja és a talaj között?
3.11. (1 pont) Képzeljük el, hogy a viharok egy év alatti összes elektromos energiáját összegyűjtjük, majd egyenletesen szétosztjuk az emberek között. Milyen hosszan tudna folyamatosan világítani egy 100 W-os izzólámpa az egy emberre jutó átlagos energiával?

Hajszálerek. Az emberi vért tekintsük olyan összenyomhatatlan, viszkózus folyadéknak, melynek

μ

(tömeg-) sűrűsége megegyezik a vízével, dinamikus viszkozitása pedig

η = 4, 5 gm^{- 1}s^{- 1}

. A hajszálér-hálózatot egyenes,

r

sugarú,

L

hosszúságú hengeres csövekkel modellezzük, és a véráram leírására a Poiseuille-féle

\begin{matrix} Δ p = R D \end{matrix}

törvényt alkalmazzuk, mely a hidrodinamikában hasonló szerepet játszik, mint az elektromosságtanban az Ohm-törvény. A fenti képletben

Δ p

az ér (cső) eleje és vége közti nyomáskülönbség, a

D = S υ

(vér-) hozam az ér

S

keresztmetszetén időegység alatt átáramlott folyadék térfogata,

υ

pedig a véráram sebessége. Az

R

áramlási ellenállást a következő formula adja meg:

\begin{matrix} R = \frac{8 η L}{π r^{4}} . \end{matrix}

Nyugalmi állapotban az emberi nagyvérkörben (amely a szív bal pitvarától a jobb kamráig vezet) a ,,vérhozam''

D \approx 100 cm^{3}s^{- 1}

. A következő kérdések megválaszolásánál a nagyvérkör leírására olyan modellt használj, melyben a hajszálerek párhuzamosan vannak kapcsolva, és mindegyikük

r = 4 μ m

sugarú,

L = 1

mm hosszúságú, és

Δ p = 1

kPa nyomáskülönbségnek van kitéve.
3.12. (1 pont) Hány hajszálér található az emberi testben?
3.13. (0,5 pont) Mekkora

υ

sebességgel áramlik a vér a hajszálerekben?

Felhőkarcoló. Egy 1000 m magas felhőkarcoló aljánál a külső levegő hőmérséklete

T_{lent} = 30^{\circ} C

. Célunk a felhőkarcoló tetejénél mérhető

T_{fent}

külső hőmérséklet megállapítása. Tekintsünk egy vékony levegőréteget (ideális nitrogéngáz, adiabatikus kitevője

γ = 7 / 5

), amely lassan

z

magasságba emelkedik, ahol a nyomás alacsonyabb, valamint tegyük föl, hogy a levegőréteg eközben adiabatikusan tágul, és így hőmérséklete a környező levegőével megegyező értékre csökken.
3.14. (0,5 pont) Határozd meg a

d T / T

relatív hőmérsékletváltozásnak és a

d p / p

relatív nyomásváltozásnak a hányadosát!
3.15. (0,5 pont) Fejezd ki a

d p

nyomáskülönbséget a

d z

magasságváltozás függvényében!
3.16. (1 pont) Mennyi a levegő hőmérséklete a felhőkarcoló tetejénél?
Adatok: A Boltzmann-állandó:

k = 1, 38 \cdot 10^{- 23} JK^{- 1}

. A nitrogénmolekula tömege:

m = 4, 65 \cdot 10^{- 26}

kg. A nehézségi gyorsulás:

g = 9, 80 ms^{- 2}

¹ A részpontszámokat azok kedvéért közöljük, akik ‐ későbbi versenyekre készülve ‐ az olimpiához hasonló feltételek mellett önállóan akarják megoldani a feladatokat. A ,,hivatalos'' megoldást és a mérési feladatot a KöMaL novemberi számában ismertetjük.
A feladatok kidolgozására 5 óra állt rendelkezésre.