Cím:	Olimpiai megjegyzések
Szerző(k):	Nagy Csaba
Füzet:	2006/december, 525 - 531. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A Minkowski-féle összeadás egy alkalmazása   A 2006. évi Matematikai Diákolimpián a legnehezebb, 6. feladatra összesen 8 darab jó megoldás született; a feladat nagyon nehéz volt. Az alábbiakban Kós Géza előadása nyomán megmutatjuk, hogy milyen tudással felvértezve, miképpen oldható meg a feladat.   6. feladat. Egy $\text{P}$ konvex sokszög mindegyik $b$ oldalához hozzárendeljük a legnagyobb területű olyan háromszög területét, aminek egyik oldala $b$ és ami benne van $\text{P}$-ben. Bizonyítsuk be, hogy a $\text{P}$ oldalaihoz rendelt területek összege legalább a kétszerese $\text{P}$ területének.   A Minkowski-féle összeadás   Értelmezni fogunk egy ponthalmazokon értelmezett kétváltozós műveletet, az úgynevezett Minkowski-féle összeadást. Ehhez a sík (vagy a tér) pontjait azonosítjuk a helyvektoraikkal. Ekkor természetes módon értelmezhetjük pontok összegét, mint a helyvektoraik összegéhez tartozó pontot. Hasonlóan, tetszőleges $P$ pont és $\lambda$ skalár esetén $\lambda P$ az a pont, amelynek $\lambda \text{p}$ a helyvektora (ahol $\text{p}$ a $P$ pont helyvektora). Ezek után az $\text{A}$ és $\text{B}$ ponthalmazok Minkowski-féle összege az $\text{A}+\text{B}=\{A+B\mid A\in \text{A}$, $B\in \text{B}\}$ halmaz. Vizsgáljuk meg ennek a műveletnek a tulajdonságait. Először is vegyük észre, hogy az alakzatok vagy az origó eltolása nem változtatja meg az összeg ,,alakját'', csak annak helyzetét. Ezért aztán amikor alakzatok összegét vizsgáljuk, akkor az origót tetszőlegesen vehetjük föl.   1. állítás. Konvex alakzatok összege is konvex.   $\text{A}+\text{B}$ akkor konvex, ha tetszőleges két pontjával együtt azok összekötő szakaszát is tartalmazza, azaz minden $C_1\mathrm{,}{C}_2\in \text{A}+\text{B}$ és $0\le \lambda \le 1$ esetén $\begin{array}{c}{\displaystyle \lambda C_1+\left(1-\lambda \right)C_2\in \text{A}+\text{B}}\end{array}$ A bizonyítás ezek után leolvasható az 1. ábráról.     1. ábra   2. állítás. Legyen $\text{A}$ és $\text{B}$ egy-egy konvex sokszög, a csúcsaik (pozitív körüljárás szerint) $A_1\mathrm{,}{A}_2\mathrm{,}\text{...}\mathrm{,}{A}_n$, illetve $B_1\mathrm{,}{B}_2\mathrm{,}\text{...}\mathrm{,}{B}_m$. Ekkor $\text{A}+\text{B}$ is konvex sokszög, a csúcsai pedig megegyeznek az $A_i+B_j$ $(1\le i\le n$, $1\le j\le m)$ pontok konvex burkának1 csúcsaival.   A definíciók alapján ez is igen egyszerűen adódik, a bizonyítást gondolja meg az olvasó. Szükségünk lesz egy újabb fogalomra: az $e$ egyenest egy síkbeli alakzat támaszegyenesének nevezünk, ha az $e$ egyik oldalán nincsen pontja az alakzatnak, de ugyanez már nem teljesül, ha az egyenest egy tetszőlegesen kicsiny vektorral eltoljuk az alakzat felé. Szemléletesen nyilvánvaló, és a megfelelő eszközök birtokában a bizonyítás sem nehéz, hogy egy korlátos alakzatnak minden iránnyal párhuzamosan két támaszegyenese van. Ha az irányokat vektorokkal adjuk meg, akkor beszélhetünk irányított támaszegyenesekről: ennek a bal oldalára esik az alakzat, amennyiben az adott vektorral azonosan irányítjuk. Korlátos alakzatnak minden irányhoz pontosan egy irányított támaszegyenese van.   3. állítás. Ha $A\in \text{A}$ és $B\in \text{B}$ pontja az $\text{A}$, illetve $\text{B}$  $\text{v}$ irányú támaszegyenesének, akkor $A+B$ is pontja az $\text{A}+\text{B}$ összeg $\text{v}$ irányú támaszegyenesének. Ennek az állításnak a megfordítása is igaz, ha $C\in \text{A}+\text{B}$ pontja az összeg $\text{v}$ irányú támaszegyenesének, akkor minden $C=A+B$, $A\in \text{A}$ és $B\in \text{B}$ felbontás esetén $A$ és $B$ szükségképpen $\text{A}$, illetve $\text{B}$ megfelelő támaszegyenesén vannak (2. ábra).     2. ábra   (A bizonyításhoz toljuk el $\text{A}$-t és $\text{B}$-t úgy, hogy az origó a támaszegyenesükre essék, majd a pontok helyvektorait bontsuk $\text{v}$-vel párhuzamos, és arra merőleges komponensekre.) $\text{A}$ és $\text{B}$ legyenek továbbra is konvex sokszögek. A 2. állításban jellemeztük az összegük csúcsait, nézzük meg, mint mondhatunk ennek a sokszögnek az oldalairól. Legyen $P$ az $\text{A}+\text{B}$ tetszőleges csúcsa, a pozitív körüljárás szerinti következő csúcs pedig legyen $Q$. Ekkor a 2. állítás szerint $P=A_s+B_t$ és $Q=A_u+B_v$ valamilyen $s$, $t$, $u$, $v$ indexekre. Egy (zárt) konvex sokszögnek egy adott irányú támaszegyenesén a sokszögnek kettő vagy egy csúcsa van aszerint, hogy a sokszögnek van a támaszegyenessel egyirányú oldalvektora (ezeket pozitív körüljárás szerint irányítjuk) vagy sem. Az előbbi esetben a két csúcs az oldal két végpontja. Mivel $P$ és $Q$ az összeg $\left(\text{q}-\text{p}\right)$ irányú támaszegyenesén vannak, a 3. állítás szerint $A_s$ és $A_u$ az $\text{A}$, $B_t$ és $B_v$ pedig a $\text{B}$ ilyen irányú támaszegyenesének pontjai. Ezért ha $A_s\ne A_u$, akkor mindkettő az $\text{A}$ sokszög $\left(\text{q}-\text{p}\right)$ irányú oldalának csúcsai, és ekkor szükségképpen $A_u=A_{s+1}$ ($A_{n+1}=A_1$). Tehát vagy $A_u=A_{s+1}$ vagy pedig $A_u=A_s$, és hasonló teljesül $B_t$-re és $B_v$-re is. Nem lehet, hogy egyszerre $A_u=A_s$ és $B_v=B_t$, mert $Q\ne P$; ha most $A_u=A_{s+1}$ és $B_v=B_{t+1}$, akkor az ${\text{a}}_u-{\text{a}}_s$ és ${\text{b}}_v-{\text{b}}_t$ oldalvektorok egyirányúak $\left(\text{q}-\text{p}\right)$-vel és ezért egymással is, és az összegük $\left(\text{q}-\text{p}\right)$. Ha $A_u=A_s$ és $B_v=B_t$ közül az egyik teljesül, akkor $\text{A}$ és $\text{B}$ közül csak az egyiknek van ilyen irányú oldalvektora, és az egyenlő $\left(\text{q}-\text{p}\right)$-vel (ha mindkét sokszögnek volna ilyen irányú oldala, akkor a $PQ$ oldalegyenesen ‐ és nem a két pont között ‐ lenne még egy $A_i+B_j$ alakú pont, ezért $PQ$ nem lenne oldala $\text{A}+\text{B}$-nek). Tehát $\text{A}+\text{B}$ minden oldalvektora oldalvektora $\text{A}$-nak vagy $\text{B}$-nek, vagy pedig $\text{A}$ és $\text{B}$ azonos irányú oldalvektorainak összege. $\text{A}+\text{B}$ konvex, ezért minden oldalvektorát egy pozitív irányú (a megfelelő külső szöggel egyenlő nagyságú) forgatás (és egy nagyítás) viszi a következőbe. Így végül igazoltuk a következőt: 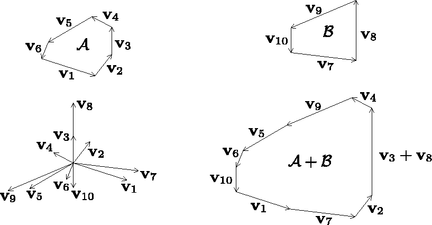  4. állítás. $\text{A}+\text{B}$-t úgy kaphatjuk meg, hogy $\text{A}$ és $\text{B}$ oldalvektorait irány szerint sorbarendezzük, majd ebben a sorrendben összefűzzük őket (3. ábra).     3. ábra   Most bebizonyítunk egy tételt, amelyet az olimpiai feladat megoldásánál fel fogunk használni.   Brunn‐Minkowski-egyenlőtlenség. Ha $\text{A}$ és $\text{B}$ konvex sokszögek, akkor $\begin{array}{c}{\displaystyle \sqrt[]{t\left(\text{A}+\text{B}\right)}\ge \sqrt[]{t\left(\text{A}\right)}+\sqrt[]{t\left(\text{B}\right)}\mathrm{,}}\end{array}$ ahol $t\left(X\right)$ az $X$ alakzat területét jelenti.   Megjegyzések. 1. A tétel igaz tetszőleges síkidomokra. A Minkowski-féle összeadás definiálható magasabb dimenziókban is, és ott is teljesül az egyenlőtlenség megfelelője, amelyben $n$-edik gyök és $n$-dimenziós térfogat szerepel. 2. A B. 3591. feladatra (a megoldás 2003/5. számunkban olvasható) mindössze 17 dolgozat érkezett, ezek közül mindössze 7 volt helyes: a feladat nehéz volt. A feladat így szólt: A konvex $ABCD$ négyszög területe $T$, egy belső pontja $P$. A $P$-n keresztül $BC$-vel húzott párhuzamos egyenes a $BA$ oldalt az $E$, az $AB$-vel húzott párhuzamos egyenes a $BC$ oldalt az $F$, az $AD$-vel húzott párhuzamos egyenes a $CD$ oldalt a $G$ pontban, a $CD$-vel húzott párhuzamos egyenes az $AD$ oldalt a $H$ pontban metszi. Jelölje az $AEPH$ négyszög területét $t_1$, a $PFCG$ négyszög területét $t_2$. Bizonyítsuk be, hogy $\sqrt[]{t_1}+\sqrt[]{t_2}\le \sqrt[]{T}$. Talán látszik a megoldás $\text{...}$   A tételt $\text{A}+\text{B}$ oldalszáma szerinti teljes indukcióval bizonyítjuk. Ha $\text{C}=\text{A}+\text{B}$ háromszög, akkor $\text{A}$, $\text{B}$ és $\text{C}$ hasonló egyállású háromszögek, ugyanis ebben az esetben az összeg oldalvektorainak előállítása miatt $\text{A}$-nak és $\text{B}$-nek nem lehet olyan oldala, amely nem párhuzamos $\text{C}$ valamelyik oldalával. Az állítás ekkor egyenértékű azzal, hogy $\text{A}$ és $\text{B}$ megfelelő oldalainak összege $\text{C}$ megfelelő oldalának a hossza, hiszen a jól ismert tulajdonság szerint hasonló háromszögek területének aránya a hasonlóság (és így az oldalak) arányának a négyzete. Ha $\text{A}+\text{B}$ paralelogramma, akkor $\text{A}$ és $\text{B}$ is paralelogramma, mégpedig ugyanolyan oldalirányokkal. $\text{A}$ és $\text{B}$ oldalainak hossza legyen $p$ és $q$, illetve $r$ és $s$, az oldalak szöge pedig $\alpha$. Ekkor $\text{C}$ oldalai $p+r$ és $q+s$ hosszúak, a szögük $\alpha$, az állítás pedig: $\sqrt[]{\left(p+r\right)\left(q+s\right)\text{sin}\alpha }\ge \sqrt[]{pq\text{sin}\alpha }+\sqrt[]{rs\text{sin}\alpha }$. Ehhez az kell, hogy $\left(p+r\right)\left(q+s\right)\ge pq+rs+2\sqrt[]{pqrs}$, azaz $\frac{ps+qr}{2}\ge \sqrt[]{ps\cdot qr}$, ez pedig teljesül a számtani és mértani közép közti összefüggés miatt. Tegyük fel, hogy $\text{A}+\text{B}$ nem háromszög és nem is paralelogramma, és az állítás igaz kisebb oldalszám esetén. Könnyen látható, hogy ekkor $\text{A}+\text{B}$-nek van két olyan szomszédos szöge, amelyeknek az összege nagyobb, mint ${180}^{\circ }$. Tekintsük azt a $d$ oldalt, amely ennek a két szögnek a közös szára és a vele szomszédos két oldalt meghosszabbítva rajzoljunk rá ,,kifelé'' egy $\tilde{\text{C}}$ háromszöget, majd az $\text{A}$ és a $\text{B}$  $d$-vel egyirányú oldalára rajzoljuk meg a $\tilde{\text{C}}$-vel egyállású, $\tilde{\text{A}}$ és $\tilde{\text{B}}$ háromszögeket (4. ábra).     4. ábra   $\text{A}$ és $\text{B}$ közül legalább az egyiknek van $d$ irányú oldala. Ha a másiknak ‐ mondjuk $\text{A}$-nak ‐ nincsen, akkor azt a csúcsát, amelyiken átmegy az adott oldallal egyirányú támaszegyenese, tekintsük egy $0$ hosszúságú oldalnak. (Ekkor $\tilde{\text{A}}$ egyetlen ponttá fajul.) Az így keletkező sokszögek közül az első, $\left(\text{A}+\text{B}\right)\text{'}$ nyilvánvalóan konvex, és felhasználva a 4. állításnak az $\text{A}+\text{B}$ oldalvektorainak a sorrendjére vonatkozó részét könnyen látható, hogy a másik kettő, $\text{A}\text{'}$ és $\text{B}\text{'}$ is azok. $\left(\text{A}+\text{B}\right)\text{'}$-nek nyilván kevesebb oldala van, mint $\left(\text{A}+\text{B}\right)$-nek, végül az olvasóra hagyjuk annak bizonyítását, hogy $\left(\text{A}+\text{B}\right)\text{'}=\text{A}\text{'}+\text{B}\text{'}$. Legyen ezután $t\left(\text{A}\right)=a^2$, $t\left(\text{B}\right)=b^2$, $t\left(\text{A}+\text{B}\right)=c^2$, $t\left(\tilde{\text{A}}\right)={\tilde{a}}^2$ és $t\left(\tilde{\text{B}}\right)={\tilde{b}}^2$; $\tilde{\text{C}}$, $\tilde{\text{A}}$ és $\tilde{\text{B}}$ hasonlósága miatt $t\left(\tilde{\text{C}}\right)={\left(\tilde{a}+\tilde{b}\right)}^2$. Az $\left(\text{A}+\text{B}\right)\text{'}$ sokszögnek kevesebb oldala van, mint $\left(\text{A}+\text{B}\right)$-nek, ezért alkalmazhatjuk az indukciós feltevést az $\text{A}\text{'}$ és $\text{B}\text{'}$ sokszögekre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{t\left(\text{A}+\text{B}\right)\text{'}}}& {\displaystyle \ge \sqrt[]{t(\text{A')}}+\sqrt[]{t(\text{B')}}\mathrm{,}\text{azaz}}\hfill \\ \hfill {\displaystyle \sqrt[]{t\left(\text{A}+\text{B}\right)+t\left(\tilde{\text{C}}\right)}}& {\displaystyle \ge \sqrt[]{t(\text{A)}+t\left(\tilde{\text{A}}\right)}+\sqrt[]{t(\text{B)}+t\left(\tilde{\text{B}}\right)}\mathrm{.}}\hfill \end{array}}$ Jelöléseinkkel felírva $\sqrt[]{c^2+(\tilde{a}+\tilde{b}{)}^2}\ge \sqrt[]{a^2+{\tilde{a}}^2}+\sqrt[]{b^2+{\tilde{b}}^2}$. A jobb oldal alulról becsülhető, ha felírjuk a háromszög-egyenlőtlenséget a $\left(0;0\right)$, $\left(a;\tilde{a}\right)$, $\left(a+b;\tilde{a}+\tilde{b}\right)$ pontok által meghatározott háromszögre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{\left(a^2+{\tilde{a}}^2\right)}+\sqrt[]{\left(b^2+{\tilde{b}}^2\right)}}& {\displaystyle \ge \sqrt[]{{\left(a+b\right)}^2+(\tilde{a}+\tilde{b}{)}^2}\mathrm{,}\text{és így}}\hfill \\ \hfill {\displaystyle \sqrt[]{(c^2+(\tilde{a}+\tilde{b}{)}^2}}& {\displaystyle \ge \sqrt[]{{\left(a+b\right)}^2+(\tilde{a}+\tilde{b}{)}^2}\mathrm{.}}\hfill \end{array}}$ Ebből pedig következik, hogy $\begin{array}{c}{\displaystyle c\ge a+b\mathrm{,}\text{tehát valóban}\sqrt[]{t\left(\text{A}+\text{B}\right)}\ge \sqrt[]{t\left(\text{A}\right)}+\sqrt[]{t\left(\text{B}\right)}\mathrm{.}}\end{array}$ Ezzel az indukciós lépést és így a tételt igazoltuk.   Az olimpiai feladat megoldása   Tekintsük a $\text{P}-\text{P}$ sokszöget (azaz $\text{P}+\left(-\text{P}\right)$-t), ahol $-\text{P}=\left\{-P\mid P\in \text{P}\right\}$. Ez nem más, mint $\{A-B\mid A$, $B\in \text{P}\}$. Ez a sokszög szimmetrikus az origóra, mert ha $C=A-B$ pontja, akkor $-C=B-A$ is; ezen kívül független (a helye is) az origó helyzetétől, mert csak $P$ pontjainak különbsége szerepel benne. Vizsgáljuk $\text{P}-\text{P}$ oldalait. Ha valamelyik oldal $\text{P}$ és $-\text{P}$ egyirányú oldalvektorának összege (ez akkor fordul elő, ha $\text{P}$-nek van két párhuzamos oldala, mert $-\text{P}$ oldalvektorai $\text{P}$ oldalvektorainak ellentettjei), akkor vegyünk fel ezen az oldalon egy újabb csúcsot úgy, hogy az a két oldalvektorral egyenlő nagyságú részekre bontsa (és ugyanezt végezzük el ennek az oldalnak a tükörképére is, úgy, hogy a középpontos szimmetria megmaradjon). Ezekkel a csúcsokkal együtt $\left(\text{P}-\text{P}\right)$-nek kétszer annyi csúcsa lesz, mint $\text{P}$-nek, és a kerületén megjelennek $\text{P}$ és $-\text{P}$ oldalai. Kössük össze a csúcsokat az origóval. Tekintsük az így keletkező háromszögeket. Ezek mindegyike $\text{P}$ vagy $-\text{P}$ egy oldalvektorára (az utóbbi $\text{P}$ egy oldalvektorának tükörképe) illeszkedik. Bebizonyítjuk, hogy minden ilyen háromszög egybevágó a $\text{P}$ megfelelő oldalához rendelt maximális területű háromszöggel. Ebből pedig az következik, hogy $\text{P}-\text{P}$ felbontásában minden maximális területű háromszög kétszer szerepel. Legyen $\text{P}$ egyik oldala $A_i{A}_{i+1}$, az ennek az oldalnak megfelelő oldal $\left(\text{P}-\text{P}\right)$-ben $B_i{B}_{i+1}$ (5. ábra). Feltehetjük, hogy az origó az $A_i{A}_{i+1}$ oldalhoz hozzárendelt háromszög harmadik csúcsa, azaz $\text{P}$-nek az a csúcsa, amelyiken átmegy a másik $A_i{A}_{i+1}$-gyel párhuzamos támaszegyenes (ha több ilyen csúcs is van, mert $\text{P}$-ben van egy $A_i{A}_{i+1}$-gyel párhuzamos oldal, akkor majd később határozzuk meg, hogy hol legyen a maximális területű háromszög harmadik csúcsa). Ekkor $-\text{P}$  $\left({\text{a}}_{i+1}-{\text{a}}_i\right)$ irányú támaszegyenese átmegy az origón.     5. ábra   Ha $\text{P}$-nek nincs $A_i{A}_{i+1}$-gyel párhuzamos oldala, akkor $-\text{P}$ egyetlen közös pontja az ${\text{a}}_{i+1}-{\text{a}}_i$ irányú támaszegyenesével az origó. Ezért $\text{P}-\text{P}$ közös pontjai az ilyen irányú támaszegyenesével az $O+A$ alakú pontok, ahol $O$ az origó, $A$ pedig az $A_i{A}_{i+1}$ oldal pontja; ez megegyezik az $A_i{A}_{i+1}$ oldallal. Másrészt $\text{P}-\text{P}$ metszete ezzel a támaszegyenesével $B_i{B}_{i+1}$. Ebből $A_i{A}_{i+1}=B_i{B}_{i+1}$. Tehát $O{B}_i{B}_{i+1}$ egybeesik az $A_i{A}_{i+1}$ oldalhoz tartozó háromszöggel. Ennek tükörképe az origóra szintén a felbontásban szereplő háromszög, vagyis az $A_i{A}_{i+1}$-hez tartozó háromszög valóban kétszer szerepel a felbontásban. Ha $\text{P}$-nek van még egy $A_i{A}_{i+1}$-gyel párhuzamos oldala, akkor azt forgassuk el (pl. a felezőpontja körül) egy elegendően kicsi $\epsilon >0$ szöggel (6. ábra). (Ekkor $\epsilon$ függvényében $\text{P}$ oldalainak hossza is változik, illetve a csúcsok elmozdulnak, de ha $\epsilon$ tart a 0-hoz, akkor ennek a megváltozásnak a mértéke is.) Ekkor $\left(\text{P}-\text{P}\right)$-nek azok az oldalai, amelyek $\text{P}$ és $-\text{P}$ egyirányú oldalvektorainak összegei, ,,megtörnek'', úgy, hogy a két rész hossza egyenlő lesz a két oldalvektorral. Feltehetjük, hogy $\text{P}-\text{P}$ oldalain úgy választottuk meg a belső csúcsokat, hogy ezekben kerül sor erre a törésre. Hasonlóan forgassuk el a többi párhuzamos oldalpár egy-egy oldalát is. Az így kapott ${\text{P}}_{\epsilon }$ sokszögnek már nincsenek párhuzamos oldalai, ezért ${\text{P}}_{\epsilon }-{\text{P}}_{\epsilon }$ felbontásában a maximális területű háromszögek szerepelnek (mindegyikük kétszer).     6. ábra   $\text{P}$-ben a párhuzamos oldalpárok miatt nem egyértelmű az oldalakhoz rendelt maximális területű háromszögek harmadik csúcsa. ${\text{P}}_{\epsilon }$-ban viszont tudjuk, hogy melyik csúcsa lesz egy adott oldalhoz tartozó háromszög harmadik csúcsa, ezért meghatározhatjuk, hogy $\text{P}$-ben is ugyanez a csúcs legyen. Ekkor $\epsilon \ge 0$ függvényében ${\text{P}}_{\epsilon }$ csúcsainak a helye, minden hossz és terület, és az oldalakhoz rendelt háromszögek harmadik csúcsának helye is folytonosan változik, és az állítás igaz $\epsilon$ minden (elég kicsi) pozitív értékére, ezért az $\epsilon =0$, vagyis ${\text{P}}_{\epsilon }=P$ esetben is igaz. $\left(\text{P}-\text{P}\right)$-ben tehát minden maximális területű háromszög kétszer szerepel, ezért a területe az oldalakhoz hozzárendelt területek összegének kétszerese. Azt kell bebizonyítanunk, hogy ez $\text{P}$ területének legalább 4-szerese. Alkalmazzuk ehhez a Brunn‐Minkowski-egyenlőtlenséget $\text{A}=\text{P}$, $\text{B}=-\text{P}$-re: $\sqrt[]{t\left(P-\text{P}\right)}\ge \sqrt[]{t\left(\text{P}\right)}+\sqrt[]{t\left(-\text{P}\right)}=2\sqrt[]{t\left(\text{P}\right)}$. Innen $t\left(\text{P}-\text{P}\right)\ge 4t\left(\text{P}\right)$, és ezt kellett bizonyítanunk. 1 A legkisebb olyan konvex tartomány, amely tartalmazza a pontok mindegyikét.