Cím:	Hogyan szervezzünk körmérkőzéses focibajnokságot?
Szerző(k):	Kiss György
Füzet:	2006/december, 514 - 525. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1   A címben feltett kérdésre válaszolva alkalmas előkészületek után két módszert is megadunk. Ezek egyike véges geometriai, s e cikk nem titkolt célja az, hogy megismertesse az olvasót a véges geometriák néhány alapvető fogalmával.   1. Számolás egyszerűen, avagy mik azok a véges testek?   Ha egész számokkal összeadást, kivonást vagy szorzást végzünk és nem vagyunk kíváncsiak a pontos eredményre, hanem csak azt szeretnénk tudni, hogy az páros vagy páratlan, akkor ezt egyszerűen megtehetjük. Ha az elvégzendő műveletekben a páros számokat $0$-val, a páratlanokat pedig $1$-gyel helyettesítjük, majd kiszámoljuk az eredményt, akkor annak paritása meg fog egyezni az eredeti művelet eredményének paritásával, mert páros számot bármilyen másikkal szorozva az eredmény páros szám ($0$-szor bármi $0$), különböző paritású számok összege és különbsége páratlan ($\pm 1\pm 0=\pm 1$), megegyező paritású számok összege és különbsége pedig páros ($1\pm 1=0$ vagy $2$, $0\pm 0=0$). Módszerünk akkor is működik, ha $2$ helyett tetszőleges $p$ prímszámra alkalmazzuk, azaz ha a pontos eredmény helyett csak arra vagyunk kíváncsiak, hogy az $p$-vel osztva mennyi maradékot ad. Ha így szeretnénk számolni, akkor az összes egész szám helyett elegendő a $\mathrm{0,1,}\text{...}\mathrm{,}p-1$ számokkal dolgoznunk, mert minden $a$ egész helyett írhatjuk azt a számot, amit $a$ $p$-vel való osztásakor kapunk maradékul. Ennek a számolásnak egyéb érdekes tulajdonságai is vannak, ezeket foglaljuk össze a fejezet hátralévő részében. Ha az olvasó ismeri a véges testek fogalmát, akkor a cikk olvasását a 2. fejezetnél folytathatja. Legyen $p$ egy rögzített prímszám. Az egész számokat soroljuk be osztályokba aszerint, hogy mennyi maradékot adnak a $p$-vel való osztáskor. Így $p$ darab különböző osztályt kapunk, az azonos osztályban lévő számok felírhatók $np+m$ alakban, ahol $n$ végigfut az egész számok halmazán, $m$ pedig az osztályra jellemző maradék, amelyről feltehetjük, hogy $0\le m\le p-1$. Két egész szám pontosan akkor van egy osztályban, ha különbségük osztható $p$-vel. Legyen ${\text{Z}}_p=\left\{\mathrm{0,1,}\text{...}\mathrm{,}p-1\right\}$. Ekkor a ${\text{Z}}_p$ halmaz elemeit természetes módon azonosíthatjuk a fenti osztályokkal. A ${\text{Z}}_p$ elemei közt definiáljuk az összeadást és a szorzást annak megfelelően, ahogy a $p$-vel való osztáskor kapott maradékkal való számolásnál tettük: $a\oplus b=c$, illetve $a\odot b=c$, ha az egészek közt elvégezve az összeadást, illetve a szorzást, az eredményül kapott szám abba az osztályba esik, amelyiket $c$ reprezentálja. Először gondoljuk meg, hogy ez a definíció ,,jó'', azaz a műveletek eredménye csak az osztályoktól függ, és nem attól, hogy az egyes osztályoknak melyik elemét tekintjük. Ehhez azt kell belátnunk, hogy ha $a$ és $a\text{'}$, valamint $b$ és $b\text{'}$ ugyanabba az osztályba tartozik, akkor $a+b$ és $a\text{'}+b\text{'}$ is, továbbá $ab$ és $a\text{'}b\text{'}$ is ugyanabba az osztályba tartozik. Ez igaz, mert ha $p\mid a-a\text{'}$ és $p\mid b-b\text{'}$, akkor $p\mid \left(a-a\text{'}\right)+\left(b-b\text{'}\right)=\left(a+b\right)-\left(a\text{'}+b\text{'}\right)$ és $p\mid \left(a-a\text{'}\right)b+\left(b-b\text{'}\right)a\text{'}=ab-a\text{'}b\text{'}$. A kivonást és az osztást az összeadás, illetve a szorzás inverz műveleteként definiáljuk. Először megmutatjuk, hogy ${\text{Z}}_p$ minden $m$ eleméhez egyértelműen létezik egy olyan $\left(-m\right)$-mel jelölt elem, az $m$ additív inverze, melyre $m\oplus \left(-m\right)=0$. Ez az állítás nyilvánvaló, mert ha tekintjük a $p-m$ kivonás eredményét, akkor a $p$-nél kisebb nemnegatív egészek közt nyilván csak erre lesz igaz, hogy $m$-mel összeadva $p$-vel osztható számot kapunk. Vegyük észre azt is, hogy $-m=\left(p-1\right)\odot m$, azaz $-m$ tekinthető $m$ és $-1$ szorzatának (${\text{Z}}_p$-ben $-1$ az $1$ additív inverze). Tehát $m$-et úgy kell kivonni $n$-ből, hogy $n$-hez $-m$-et adunk. Az is könnyen belátható, hogy ha $0\ne m\in {\text{Z}}_p$, akkor pontosan egy olyan $m^{-1}$-nel jelölt eleme van ${\text{Z}}_p$-nek, $m$ multiplikatív inverze, amelyre $m\odot m^{-1}=1$. Az $m$-mel való szorzás ugyanis ${\text{Z}}_p$ elemeinek egy permutációját adja, mert ha $a\ne b$, akkor $m\odot a\ne m\odot b$, hiszen $m\odot a=m\odot b$ azt jelentené, hogy $p\mid ma-mb=m\left(a-b\right)$. Viszont $p$ prím (először használjuk ki ezt a tényt), ezért ebből $p\mid m$ vagy $p\mid a-b$ következik, ami ellentmondás, mert $0<m<p$ és $0<|a-b|<p$. Ha viszont az $m$-mel való szorzás ${\text{Z}}_p$ elemeinek egy permutációját adja, akkor pontosan egy olyan elem van ${\text{Z}}_p$-ben, amelyet $m$-mel szorozva $1$-et kapunk. Az $m$-mel való osztást definiáljuk tehát $m\ne 0$ esetén $m^{-1}$-nel való szorzásként, a $0$-val való osztást pedig ne engedjük meg. Mivel $m\odot 0=0$ és az $m$-mel való szorzás permutálja az elemeket, azért ha $m_1\odot m_2=0$, akkor $m_1$ és $m_2$ közül legalább az egyik $0$. Ezt a tényt röviden úgy mondjuk, hogy a szorzás nullosztómentes. Az $n\odot m^{-1}$ szorzatot a továbbiakban (a valós számoknál megszokott módon) $n/m$-mel fogjuk jelölni. Azok a műveleti tulajdonságok, melyeket a valós számok köréből ismerünk, érvényesek a ${\text{Z}}_p$ halmaz elemein most bevezetett $\oplus$ és $\odot$ műveletekre is. Összefoglalva ezeket kapjuk, hogy ($a$, $b$, $c$ tetszőleges ${\text{Z}}_p$-beli elemeket jelöl): ‐ a műveletek asszociatívak, azaz $\begin{array}{c}{\displaystyle \left(a\oplus b\right)\oplus c=a\oplus \left(b\oplus c\right)\text{és}\left(a\odot b\right)\odot c=a\odot \left(b\odot c\right);}\end{array}$ ‐ a műveletek kommutatívak, azaz $\begin{array}{c}{\displaystyle a\oplus b=b\oplus a\text{és}a\odot b=b\odot a;}\end{array}$ ‐ a műveleteknek van egységelemük, a $0$, illetve az $1$, amelyekre teljesül, hogy $\begin{array}{c}{\displaystyle a\oplus 0=0\oplus a=a\text{és}a\odot 1=1\odot a=a\mathrm{.}}\end{array}$ Minden elemnek egyértelműen létezik additív inverze, a $0$-tól különböző elemeknek pedig egyértelműen létezik multiplikatív inverzük, azaz olyan $-a$, illetve $a^{-1}$ elemek, melyekre $\begin{array}{c}{\displaystyle a\oplus \left(-a\right)=0\text{és}a\odot a^{-1}=1.}\end{array}$ Az összeadás a szorzásra nézve disztributív, azaz $\begin{array}{c}{\displaystyle a\odot \left(b\oplus c\right)=\left(a\odot b\right)\oplus \left(a\odot c\right)\mathrm{.}}\end{array}$ Ezeket a tulajdonságokat összefoglaló néven úgy mondjuk, hogy ${\text{Z}}_p$ a $\oplus$ és $\odot$ műveletekre nézve véges test. Megmutatható, hogy ha valamely $\text{F}$ véges halmazon tudunk definiálni két darab kétváltozós műveletet úgy, hogy azok kielégítik a fenti tulajdonságokat, akkor $\text{F}$ elemszáma prímhatvány. Ami ennek az állításnak a megfordítását illeti, ha $\text{F}$ elemszáma prímszám, akkor a műveletek ,,lényegében'' csak az általunk definiált $\oplus$ és $\odot$ lehetnek. Ha $\text{F}$ elemszáma valamely prímszám $1$-nél nagyobb kitevőjű hatványa, akkor is létezik a megfelelő elemszámú test, ennek előállítása azonban már bonyolultabb. Az érdeklődő olvasó ennek a [2], [3] vagy az [5] könyvekben nézhet utána. Példaként megadjuk a 4 elemű és a 9 elemű testek műveleti tábláit. A testek elemeit az egyszerűség kedvéért számokkal jelöltük, ezek a számok azonban már nem azonosíthatók a maradékos osztásnál fellépő osztályokkal. A táblázatok $i$-edik sorának és $j$-edik oszlopának kereszteződésében az $i\oplus j$, illetve $i\odot j$ értéke áll (pl. a 9 elemű testben $4\odot 6=2$). Látható, hogy a műveletek nem egyeznek meg a $4$-gyel, illetve $9$-cel való maradékos összeadással és szorzással. A szorzás esetén ezt nem is várhatjuk el, hiszen pl. két páros szám szorzata osztható $4$-gyel, de $2\odot 2\ne 0$ kell hogy teljesüljön, mert a szorzás véges testben nullosztómentes. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⊕</mo></math> }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{1 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill \\ \hfill {\displaystyle \text{2 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill \\ \hfill {\displaystyle \text{3 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill \end{array}}{\displaystyle \begin{array}{ccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⊙</mo></math> }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill \\ \hfill {\displaystyle \text{1 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{2 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill \\ \hfill {\displaystyle \text{3 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill \end{array}}}\end{array}$ $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cccccccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⊕</mo></math> }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill \\ \hfill {\displaystyle \text{0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill \\ \hfill {\displaystyle \text{1 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill \\ \hfill {\displaystyle \text{2 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill \\ \hfill {\displaystyle \text{3 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill \\ \hfill {\displaystyle \text{4 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill \\ \hfill {\displaystyle \text{5 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill \\ \hfill {\displaystyle \text{6 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill \\ \hfill {\displaystyle \text{7 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{8 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill \end{array}}{\displaystyle \begin{array}{cccccccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⊙</mo></math> }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill \\ \hfill {\displaystyle \text{0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill \\ \hfill {\displaystyle \text{1 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill \\ \hfill {\displaystyle \text{2 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill \\ \hfill {\displaystyle \text{3 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill \\ \hfill {\displaystyle \text{4 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill \\ \hfill {\displaystyle \text{5 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill \\ \hfill {\displaystyle \text{6 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill \\ \hfill {\displaystyle \text{7 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill \\ \hfill {\displaystyle \text{8 }}\hfill & \hfill {\displaystyle \text{ 0 }}\hfill & \hfill {\displaystyle \text{ 8 }}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill & \hfill {\displaystyle \text{ 2 }}\hfill & \hfill {\displaystyle \text{ 7 }}\hfill & \hfill {\displaystyle \text{ 3 }}\hfill & \hfill {\displaystyle \text{ 1 }}\hfill & \hfill {\displaystyle \text{ 6 }}\hfill & \hfill {\displaystyle \text{ 5 }}\hfill \end{array}}}\end{array}$ A véges testek elemeivel tehát lényegében ugyanúgy számolhatunk, mint a valós számokkal. A továbbiakban az $\oplus$ és $\odot$ jelölések helyett a szokásos összeadás és szorzás jelét fogjuk használni. A műveletek sorrendje is ugyanaz, mint a valós számok esetén, azaz hatványozás, szorzás‐osztás, összeadás‐kivonás.   2. Véges affin síkok   Sok geometriai kérdésre ad egyszerű megoldási módot a koordinátageometria. Ilyenkor a valós számok műveleti tulajdonságait felhasználva bizonyítunk geometriai állításokat. Mivel a véges testek rendelkeznek a legfontosabb klasszikus műveleti tulajdonságokkal, azért természetesnek tűnik az a kérdés, hogy lehet-e véges testek és a klasszikus koordinátageometria keresztezésével valami geometria-szerűséget előállítani. A válasz igen, így készíthetjük el a véges affin síkokat. Legyen ${\text{<span style="font-weight: bold;">F</span>}}_q$ valamely rögzített $q$ elemű véges test. A $q$-adrendű affin sík, amit a szokásos módon $AG\left(\mathrm{2,}q\right)$-val jelölünk, a következő: Nevezzük pontoknak az összes olyan rendezett $\left(a\mathrm{,}b\right)$ párt, ahol $a\mathrm{,}b\in {\text{<span style="font-weight: bold;">F</span>}}_q$ (a klasszikus esetben a sík pontjai a valós számokból készített rendezett pároknak felelnek meg). Az egyenesek kétfélék: egyrészt az $\left[m\mathrm{,}k\right]$ típusú rendezett párok, ahol $m\mathrm{,}k\in {\text{<span style="font-weight: bold;">F</span>}}_q$, másrészt a $\left[c\right]$ típusú elemek, ahol $c\in {\text{<span style="font-weight: bold;">F</span>}}_q$. (A klasszikus esetben a sík nem függőleges egyenesei egyértelműen megadhatók $m$ meredekségükkel és azzal a $\left(\mathrm{0,}k\right)$ ponttal, ahol az $Y$ tengelyt metszik, míg a függőleges egyenesek egyértelműen leírhatók azzal a $\left(c\mathrm{,0}\right)$ ponttal, ahol az $X$ tengelyt metszik). A véges síkon definiálnunk kell az illeszkedést is, azaz meg kell mondanunk, hogy egy pont mikor van rajta egy egyenesen. Az $\left(a\mathrm{,}b\right)$ pont akkor és csak akkor legyen rajta az $\left[m\mathrm{,}k\right]$ egyenesen, ha teljesül, hogy $b=ma+k$, a $\left[c\right]$ egyenesen pedig pontosan akkor, ha $a=c$. A klasszikus esethez hasonlóan azt mondjuk, hogy az $\left[m\mathrm{,}k\right]$ egyenes egyenlete $Y=mX+k$, illetve a $\left[c\right]$ egyenes egyenlete $X=c$. Az illeszkedés helyett gyakran fogjuk használni a geometriában megszokott fogalmakat, pl. beszélünk két pont összekötő egyeneséről: ezen olyan egyenest értünk, amely mindkét pontra illeszkedik.   1. állítás. Az $AG\left(\mathrm{2,}q\right)$ síkon $q^2$ darab pont és $q^2+q$ darab egyenes van. Bármely két különböző pontnak egyértelműen létezik összekötő egyenese.   Bizonyítás. A pontok száma megegyezik az ${\text{<span style="font-weight: bold;">F</span>}}_q$ elemeiből képezhető rendezett párok számával, ami $q^2$, mert ${\text{<span style="font-weight: bold;">F</span>}}_q$-nak $q$ eleme van. Ugyanezért az $\left[m\mathrm{,}k\right]$ típusú egyenesek száma is $q^2$. Az összes egyenes száma ennél $q$-val több, mert $\left[c\right]$ típusú egyenesből pontosan annyi van, ahány eleme van ${\text{<span style="font-weight: bold;">F</span>}}_q$-nak. Legyen $\left(a_1\mathrm{,}{b}_1\right)$ és $\left(a_2\mathrm{,}{b}_2\right)$ két különböző pont. Ha $a_1=a_2$, akkor a $\left[c\right]$ típusú egyenesek közül az $X=a_1$ egyenletű mindkét pontra illeszkedik. Más $\left[c\right]$ típusú egyenes nyilván nem illeszkedik a pontokra, és $\left[m\mathrm{,}k\right]$ típusú sem, mert ha az $Y=mX+k$ mindkét ponton átmenne, akkor $b_1=m{a}_1+k=m{a}_2+k=b_2$, azaz a két pont nem lenne különböző. Ha $a_1\ne a_2$, akkor $\left[c\right]$ típusú egyenes nyilván nem kötheti össze a pontokat. Ha valamely $Y=mX+k$ egyenletű egyenes mindkét ponton átmegy, az azt jelenti, hogy $\begin{array}{c}{\displaystyle b_1=m{a}_1+k\text{és}{b}_2=m{a}_2+k\mathrm{.}}\end{array}$ Ezekből következik, hogy $-b_2=-\left(m{a}_2+k\right)=-m{a}_2-k$, s ezért $\begin{array}{c}{\displaystyle b_1-b_2=m{a}_1+k-m{a}_2-k=m{a}_1-m{a}_2+k-k=m{a}_1-m{a}_2=m\left(a_1-a_2\right)\mathrm{.}}\end{array}$ Mivel $a_1\ne a_2$, azért létezik ${\left(a_1-a_2\right)}^{-1}$, így kapjuk, hogy $\begin{array}{c}{\displaystyle m=\frac{b_1-b_2}{a_1-a_2}\text{és}k=b_1-a_1\frac{b_1-b_2}{a_1-a_2}=\frac{b_2{a}_1-a_2{b}_1}{a_1-a_2}\mathrm{.}}\end{array}$ Tehát csak az az $\left[m\mathrm{,}k\right]$ típusú egyenes mehet át mindkét ponton, melynek egyenlete $\begin{array}{c}{\displaystyle Y=\frac{b_1-b_2}{a_1-a_2}X+\frac{b_2{a}_1-a_2{b}_1}{a_1-a_2}\mathrm{.}}\end{array}$ (1) Egyszerű számolással adódik, hogy ezt az egyenletet mindkét pont koordinátái ki is elégítik.  $\square$   A bizonyítás végén kiszámolt egyenlet formálisan megegyezik a klasszikus esetben kapott egyenlettel, hiszen a valós síkon az $\left(a_1\mathrm{,}{b}_1\right)$ és az $\left(a_2\mathrm{,}{b}_2\right)$ koordinátájú pontok összekötő egyenesének egyenlete $a_1\ne a_2$ esetén éppen (1).   2. állítás. Az $AG\left(\mathrm{2,}q\right)$ sík minden egyenesén $q$ pont van és minden ponton $q+1$ egyenes megy át.   Bizonyítás. Az $\left(a\mathrm{,}b\right)$ pont pontosan akkor van rajta az $X=c$ egyenletű egyenesen, ha $a=c$. Mivel ekkor $b$ tetszőleges, azért $q$ különböző értéket vehet fel, tehát az egyenesen $q$ pont van. Az $Y=mX+k$ egyenletű egyenesen pedig akkor van rajta a pont, ha $b=ma+k$. Azaz $a$ tetszőlegesen választható, ez $q$ lehetőség, $a$ választása viszont már meghatározza $b$-t. Tehát az ilyen típusú egyeneseken is $q$ pont van. Legyen most $P$ egy tetszőleges pont, a rajta átmenő egyenesek száma pedig $t$. Ezen egyenesek mindegyike $q-1$ darab $P$-től különböző pontot tartalmaz. E pontok egymástól is különböznek, mert az 1. állítás szerint két különböző ponton át pontosan egy egyenes megy. Tehát a síkon összesen $1+t\left(q-1\right)$ pont van. Viszont szintén az 1. állításból következik, hogy ez a szám $q^2$. Tehát $\begin{array}{c}{\displaystyle 1+t\left(q-1\right)=q^2\mathrm{,}}\end{array}$ amiből kapjuk, hogy $t=q+1$.  $\square$   Nevezzük az $e$ és $f$ egyeneseket párhuzamosaknak, ha nincs közös pontjuk, vagy ha egybeesnek. Ez megfelel a párhuzamosság klasszikus definíciójának. A következő állítás is hasonlít az euklidészi geometria megfelelő tételére:   3. állítás. Ha az $AG\left(\mathrm{2,}q\right)$ sík $P$ pontja nincs rajta a sík $e$ egyenesén, akkor $P$-n át pontosan egy $e$-vel párhuzamos egyenes megy. A sík egyenesei párhuzamossági osztályokba sorolhatók úgy, hogy két egyenes pontosan akkor van egy osztályban, ha párhuzamosak. Minden osztályban $q$ darab egyenes van, a sík minden pontján át minden osztályból pontosan egy egyenes megy.   Bizonyítás. A 2. állítás szerint $P$-n át $q+1$ egyenes megy. Az $e$ egyenesen $q$ különböző pont van, ezeket $P$-vel összekötve összesen $q$ darab $e$-t metsző és $P$-n átmenő egyenest kapunk. Vagyis $P$-n át $\left(q+1\right)-q=1$ darab $e$-t nem metsző egyenes megy. Legyen most $e$ és $f$ két tetszőleges, de különböző egyenes, amelyek az $M$ pontban metszik egymást. Az $f$ egyenesen $q-1$ darab $M$-től különböző pont van, legyenek ezek $F_1\mathrm{,}{F}_2\mathrm{,}\text{...}\mathrm{,}{F}_{q-1}$. Az előzőek szerint minden $F_i$ ponthoz pontosan egy olyan $e_i$ egyenes van, amelyik átmegy rajta és párhuzamos $e$-vel. Az $e_i$ egyenesek egymással is párhuzamosak, mert ha $i\ne j$ esetén az $N$ pont $e_i$-n is és $e_j$-n is rajta lenne, akkor $N$-en át két $e$-vel párhuzamos egyenes is menne, hiszen $e_i$ is és $e_j$ is ilyen. Ez viszont ellentmond állításunk már bizonyított első részének. Tehát $e$ osztályában, s mivel $e$ tetszőleges volt, így minden párhuzamossági osztályban $q$ darab egyenes van. Mivel minden egyenesre $q$ pont illeszkedik, azért az is igaz, hogy a sík minden pontján át minden osztályból pontosan egy egyenes megy.  $\square$   A legegyszerűbb esetekben, amikor $q$ kicsi, könnyen ,,lerajzolhatjuk'' az $AG\left(\mathrm{2,}q\right)$ síkot. A klasszikus síkkal való analógia akkor látszik a legjobban, ha a pontokat a szokásos derékszögű koordinátarendszer azon rácspontjainak választjuk, melyeknek mindkét koordinátája a $\left\{\mathrm{0,1,}\text{...}\mathrm{,}q-1\right\}$ halmazból való. Ekkor persze a véges sík egyenesei az euklidészi síkon már nem lesznek egyenesek, de hasonlítanak azokra, és a párhuzamosság is jól szemléltethető. A $q=2$, $q=3$ esetek egyszerűek, ezek láthatók az 1. ábrán. 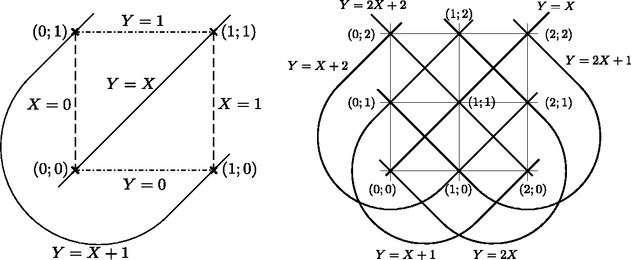    1. ábra   Ha $q=5$, akkor érdemesebb az egyes párhuzamossági osztályokat külön-külön lerajzolni, egyébként az ábra már áttekinthetetlenné válna. Ez látható a 2. ábrán.     2. ábra   A valós síkon nemcsak az egyenesek, hanem különféle görbék is megadhatók az egyenletükkel. Azok az egyenletek, melyekben $X$-nek és $Y$-nak csak elsőfokú kifejezése szerepel, azaz az $AX+BY+C=0$ ($A$ és $B$ egyszerre nem 0) típusú egyenletek mindig egyenesek egyenletei. A legegyszerűbb nem ilyen egyenlet az $Y=X^2$. Ez a valós síkon parabolát határoz meg. Vizsgáljuk meg, hogy mit mondhatunk erről az egyenletről, azaz az általa meghatározott ponthalmazról véges affin síkokon. A fejezet hátralévő részében szereplő tételek minden olyan $AG\left(\mathrm{2,}q\right)$ síkon igazak, ahol $q$ páratlan prímhatvány, a bizonyítások azonban egyszerűbbek, ha prímhatványok helyett csak prímeket tekintünk. Az érdeklődő olvasó a prímhatvány esetre vonatkozó bizonyításokat megtalálja pl. a [3] vagy [4] könyvekben. Legyen tehát $p$ páratlan prím. Ekkor a $p$ elemű testet azonosíthatjuk ${\text{Z}}_p$-vel. Tekintsük az $AG\left(\mathrm{2,}p\right)$ síkon az $Y=X^2$ egyenletnek eleget tevő pontokat. Az egyszerűség kedvéért a továbbiakban ezt a ponthalmazt $p$-edrendű parabolának nevezzük, ha pedig egy pont benne van a halmazban, akkor azt mondjuk, hogy a pont rajta van a parabolán.   4. állítás. A $p$-edrendű parabolának $p$ pontja van, ezek közül a sík bármely egyenese legfeljebb kettőt tartalmaz.   Bizonyítás. A sík $\left(a\mathrm{,}b\right)$ pontja akkor és csak akkor van rajta a $p$-edrendű parabolán, ha $b=a^2$. A pont első koordinátája tehát meghatározza a másodikat. Mivel $a$ tetszőleges, azért a parabolán lévő pontok száma megegyezik a véges test elemeinek számával, tehát $p$. Vizsgáljuk most meg egy egyenes és a parabola közös pontjait. Ha az egyenes $\left[c\right]$ típusú, akkor a közös pontok száma 1, mert a közös pontok koordinátái kielégítik az $X=c$ és az $Y=X^2$ egyenleteket is, s e két egyenletnek csak a $\left(c\mathrm{,}{c}^2\right)$ pont tesz eleget (a klasszikus síkon is ugyanígy látjuk be, hogy egy függőleges egyenesnek pontosan egy pontja van a parabolán). Ha az egyenes $\left[m\mathrm{,}k\right]$ típusú, akkor a közös pontok koordinátáira $Y=mX+k$ és $Y=X^2$ is teljesül, vagyis $X^2=mX+k$ is igaz. Próbáljuk megoldani ezt a másodfokú egyenletet. A valós esetből ismert megoldóképletet nem tudjuk alkalmazni, hiszen abban négyzetgyökvonás szerepel, amit véges test elemein egyelőre nem értelmeztünk. Megpróbálhatjuk viszont követni azt az utat, ahogy bebizonyítottuk a megoldóképletet. Vigyük az ismeretlent tartalmazó tagokat az egyenlet bal oldalára és egészítsük ki az ott szereplő kifejezést teljes négyzetté (az ${\left(a-b\right)}^2=a^2-2ab+b^2$ azonosság véges testekben is igaz, ha a $2$-vel jelölt elem az $1+1$ összeadás eredménye). Mivel $p$ páratlan, azért $1+1=2\ne 0$ és $2\cdot 2=4\ne 0$ (ha $p=3$, akkor ‐ mint láttuk ‐ $4$ helyett $1$-et kell írnunk), ezért ezekkel az elemekkel oszthatunk. Egyenletünk tehát $\begin{array}{c}{\displaystyle X^2-mX+\frac{m^2}{4}=k+\frac{m^2}{4}\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle {\left(X-\frac{m}{2}\right)}^2=k+\frac{m^2}{4}}\end{array}$ (2) alakra hozható. Most kellene négyzetgyököt vonni. Ehhez némi előkészületre van szükségünk. Ha ${\text{Z}}_p$ elemeit négyzetre emeljük, akkor $\left(p+1\right)/2$ különböző elemet kapunk. A szorzás asszociativitása és kommutativitása miatt ugyanis ${\left(-a\right)}^2={\left(-1\right)}^2{a}^2=a^2$, tehát a $0$-tól különböző elemek párokba állíthatók úgy, hogy az egyes párokban lévő elemek négyzete megegyezik. Különböző párokhoz tartozó elemek négyzete viszont különböző, mert ha $a^2=b^2$, akkor $a^2-b^2=\left(a-b\right)\left(a+b\right)=0$, vagyis a nullosztómentesség miatt vagy $a=b$ vagy $a=-b$. A párok száma $\left(p-1\right)/2$, ehhez kell még a $0$-t hozzáadni, s így kapunk $\left(p+1\right)/2$ különböző elemet. Tehát pontosan egy olyan elem van, amelynek a négyzete $0$, a nemnulla elemek fele nem áll elő ${\text{Z}}_p$-beli elem négyzeteként ‐ ezeket a továbbiakban nemnégyzet elemeknek nevezzük ‐, másik fele viszont pontosan két ${\text{Z}}_p$-beli elem négyzete, ezeket a továbbiakban négyzetelemeknek nevezzük. (A valós számok esetén a nemnégyzetek a negatív, a négyzetek pedig a pozitív számok). A (2) egyenletnek tehát nincs megoldása, ha a bal oldalon nemnégyzet elem áll, 1 megoldása van, ha a bal oldalon $0$ van, és két megoldása van, ha a bal oldalon négyzetelem áll. A $p$-edrendű parabolának és az $Y=mX+k$ egyenesnek ezért nincs közös pontja, ha $k+m^2/4$ nemnégyzet. Ha $k+m^2/4=0$, akkor egyetlen közös pontjuk van, ez az $\left(m/\mathrm{2,}{m}^2/4\right)$, ha pedig $k+m^2/4$ négyzetelem, akkor a közös pontok száma kettő, ezek $\left(m/2+d\mathrm{,}{m}^2/4+md+d^2\right)$ és $\left(m/2-d\mathrm{,}{m}^2/4-md+d^2\right)$, ahol $d^2=k+m^2/4$.  $\square$   A valós síkon a parabolának minden $P$ pontjában van érintőegyenese. Ez az a nem függőleges egyenes, amelyiknek a parabolával csak egy közös pontja van, $P$. Különböző pontokhoz tartozó érintők nem párhuzamosak, a függőleges irányt kivéve minden irányú érintője van a parabolának. Ezek a $p$-edrendű parabolára is igazak.   5. állítás. A $p$-edrendű parabola tetszőleges $T$ pontján át $p-1$ olyan egyenes megy, amelyik két pontban metszi a parabolát és két olyan, amelyik csak $T$-ben. A $\left[c\right]$ típusú egyenesek mindegyike egy pontban metszi a parabolát, a többi párhuzamossági osztály mindegyikében pontosan egy olyan egyenes van, amelyik egy pontot tartalmaz a paraboláról.   Bizonyítás. Tudjuk, hogy $T$-n át $p+1$ egyenes megy. A parabolának $p-1$ $T$-től különböző pontja van, ezeket $T$-vel összekötve csupa különböző egyenest kapunk, mert a 4. állítás szerint egyetlen egyenes sem metszheti kettőnél több pontban a parabolát. Tehát $T$-n át $p-1$ darab két pontban metsző egyenes megy, a maradék $\left(p+1\right)-\left(p-1\right)=2$ egyenes pedig csak $T$-ben metszi a parabolát. Azt már beláttuk, hogy a $\left[c\right]$ típusú egyenesek mindegyike egy pontban metszi a parabolát. A 4. állítás bizonyítása során azt is kiszámoltuk, hogy az $Y=mX+k$ egyenesnek pontosan akkor van egy közös pontja a parabolával, ha $k+m^2/4=0$. Ha tehát $m$-et rögzítjük, azaz egy párhuzamossági osztály egyeneseit tekintjük, akkor pontosan egy egyenesnek, az $Y=mX-m^2/4$ egyenletűnek lesz egy közös pontja a parabolával. (Ez a pont $\left(m/\mathrm{2,}{m}^2/4\right)$.)  $\square$   A továbbiakban a $p$-edrendű parabola érintőjének nevezzük azokat az $\left[m\mathrm{,}k\right]$ típusú egyeneseket, melyeknek egy közös pontjuk van a parabolával. Az $\left(a\mathrm{,}{a}^2\right)$ pontban tehát a parabola érintőjének egyenlete $Y=2aX-a^2$, ami formálisan ugyanaz, mint a valós sík esetén. A 3. ábrán $p=5$ esetén látható a parabola és az egyes párhuzamossági osztályokhoz tartozó érintői. 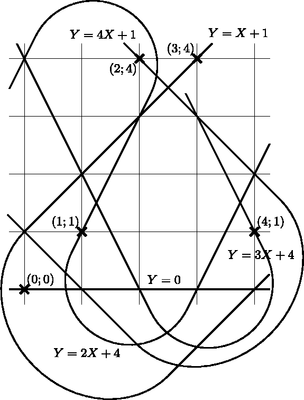    3. ábra   Ebben az esetben a négyzetelemek 1, 4; a nemnégyzetek 2, 3. A parabola pontjai $\left(\mathrm{0,0}\right)$, $\left(\mathrm{1,1}\right)$, $\left(\mathrm{2,4}\right)$, $\left(\mathrm{3,4}\right)$ és $\left(\mathrm{4,1}\right)$, az egyes pontokban az érintők egyenlete pedig rendre $Y=0$, $Y=2X+4$, $Y=4X+1$, $Y=X+1$ és $Y=3X+4$.   3. A focibajnokság szervezése   Most már mindent tudunk ahhoz, hogy nekilássunk a focibajnokság megszervezéséhez. Körmérkőzéses bajnokságban minden csapat minden másikkal pontosan egyszer találkozik. A bajnokságot fordulókra osztják, minden fordulóban minden csapat egy meccset játszik. Ez azt jelenti, hogy a csapatok száma páros. (Páratlan számú csapat esetén minden fordulóban egy csapat pihen, ezért ha benevezünk egy virtuális csapatot, amelyiknek a neve PIHEN FC, akkor a bajnokság megszervezését visszavezettük a páros sok résztvevő esetére.) Ha a csapatok száma kicsi, akkor könnyű dolgunk van. Két csapat esetén csak egy meccs van. Ha négy csapatunk van, $A$, $B$, $C$ és $D$, akkor lényegében egyféleképp szervezhető a bajnokság, mert minden fordulót egyértelműen meghatároz az, hogy $A$ kivel játszik: ${\displaystyle \begin{array}{ccc}{\displaystyle \text{ 1. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill \\ {\displaystyle \text{ 2. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill \\ {\displaystyle \text{ 3. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math> }}\hfill \end{array}}$   Ha még két csapat, $E$ és $F$ is benevez, akkor már kicsit bonyolultabb a helyzet. Ha például úgy kezdődne a bajnokság, hogy ${\displaystyle \begin{array}{cccc}{\displaystyle \text{ 1. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill \\ {\displaystyle \text{ 2. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill \\ {\displaystyle \text{ 3. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math> }}\hfill \end{array}}$   akkor abban a fordulóban, amelyikben az $A$‐$D$ meccsre sor kerülne, $E$ nem tudna kivel játszani, mert $B$-vel, $C$-vel és $F$-fel már találkozott. Rövid próbálkozás után persze itt is találunk megoldást, pl: ${\displaystyle \begin{array}{cccc}{\displaystyle \text{ 1. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill \\ {\displaystyle \text{ 2. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill \\ {\displaystyle \text{ 3. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math>}}\hfill \\ {\displaystyle \text{ 4. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill \\ {\displaystyle \text{ 5. forduló:}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>F</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi></math>‐<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>E</mi></math> }}\hfill \end{array}}$   Meg lehet mutatni (lásd pl. [1]), hogy hat lényegében különböző bajnokság szervezhető. A legtöbb bajnokságban azonban hatnál jóval több csapat szerepel. Az európai elsőosztályú focibajnokságok közül sokban 20 (pl. olasz, spanyol) vagy 18 (német, francia) csapat szerepel. Ezekben a számokban az a közös, hogy felírhatók $p+1$ alakban, ahol $p$ páratlan prím. Ilyen létszám mellett könnyen megszervezhető a bajnokság a $p$-edrendű parabola tulajdonságait felhasználva. Bajnokság $p+1$ csapattal. Tekintsük az $AG\left(\mathrm{2,}p\right)$ síkon a $p$-edrendű parabolát. Legyenek ennek pontjai $A_0\mathrm{,}{A}_1\mathrm{,}\text{...}\mathrm{,}{A}_{p-1}$, ahol az indexeket úgy választjuk, hogy a parabola $A_i$-beli érintője párhuzamos legyen a sík $Y=iX$ egyenletű egyenesével minden $i\in {\text{Z}}_p$ esetén. A bajnokságban szereplő csapatok közül $p$ darabot feleltessünk meg a parabola pontjainak, egy csapatot pedig egy $\left(\infty \right)$ jelnek. A fordulókat feleltessük meg a sík párhuzamos egyenesei által alkotott osztályoknak úgy, hogy a $\left[c\right]$ típusú egyenesek osztálya nem felel meg fordulónak. A többi párhuzamossági osztály mindegyike egyértelműen jellemezhető azzal az $m\in {\text{Z}}_p$ értékkel, amelyik az adott osztályba tartozó egyenesek egyenletében $X$ együtthatója. Tehát beszélhetünk az $m$ meredekséghez tartozó fordulóról. Ebben az ${\text{F}}_m$-mel jelölt fordulóban a csapatok párosítása legyen a következő: $A_m$‐$\left(\infty \right)$ és $A_i$‐$A_j$ pontosan akkor, ha az $A_i{A}_j$ egyenes egyenlete $Y=mX+k$ alakú. Megmutatjuk, hogy így egy jó lebonyolítást kapunk. A fordulók száma eggyel kisebb, mint a csapatok száma. Minden $m\in {\text{Z}}_p$ esetén igaz, hogy az ${\text{F}}_m$ fordulóban minden csapat pontosan egy meccset játszik, mert a parabola tetszőleges $A_i$ pontján át az 5. állítás szerint pontosan egy $m$ meredekségű egyenes megy. Ha ez az érintő, akkor $i=m$ és $A_i$ ellenfele $\left(\infty \right)$ ha pedig $i\ne m$, akkor az $A_i$-n átmenő $m$ meredekségű egyenes a 4. állítás szerint a parabolának még pontosan egy $A_j\ne A_i$ pontját tartalmazza, s az ennek megfelelő csapattal játszik $A_i$ az ${\text{F}}_m$ fordulóban. Az is látszik, hogy bármely két csapat pontosan egyszer találkozik a bajnokság során. Ez $\left(\infty \right)$ esetén az 5. állításnak abból a részéből következik, amely szerint a $\left[c\right]$ típusú egyenesek osztályát kivéve a parabolának minden párhuzamossági osztályban pontosan egy érintője van; $A_i$ és $A_j$ esetén pedig az 5. állítás azon részéből, mely szerint a $\left[c\right]$ típusú egyenesek egy pontban metszik a parabolát, azaz az $A_i{A}_j$ egyenes nem ilyen, tehát egyenlete $Y=mX+k$ alakú, s ezért a meccsre az ${\text{F}}_m$ fordulóban sor kerül. Az $AG\left(\mathrm{2,}q\right)$ sík parabolájából kiindulva ugyanezzel a módszerrel lehet megszervezni a bajnokságot pl. Máltán, ahol $10=3^2+1$ csapat van az első osztályban. A magyar NB I-ben viszont 16 csapat szerepel, ezért ott módszerünk nem működik. Az ilyen ,,nem jó'' bajnokságokat is meg lehet persze szervezni. Erre a legegyszerűbb módszer a következő ($n>1$ tetszőleges egész szám): Bajnokság $2n$ csapattal. Tekintsünk az euklidészi síkon egy szabályos $\left(2n-1\right)$-szöget. Legyenek ennek csúcspontjai $A_1\mathrm{,}{A}_2\mathrm{,}\text{...}\mathrm{,}{A}_{2n-1}$. A bajnokságban szereplő csapatok közül $2n-1$ darabot feleltessünk meg a sokszög csúcspontjainak, egy csapatot pedig a sokszög köré írható kör $K$ középpontjának. A fordulókat feleltessük meg a $K{A}_m$ irányoknak, ahol $m=\mathrm{1,2,}\text{...}\mathrm{,2}n-1$. Ekkor beszélhetünk az $m$ indexhez tartozó fordulóról. Ebben az ${\text{F}}_m$-mel jelölt fordulóban a csapatok párosítása legyen a következő (lásd a 4. ábrát).     4. ábra   $A_m$‐$K$ és $A_i$‐$A_j$ pontosan akkor, ha az $A_i{A}_j$ egyenes merőleges az $A_{m}K$ egyenesre. Megmutatjuk, hogy így egy jó lebonyolítást kapunk. A fordulók száma eggyel kisebb, mint a csapatok száma. Minden $m=\mathrm{1,2,}\text{...}\mathrm{,2}n-1$ esetén igaz, hogy az ${\text{F}}_m$ fordulóban minden csapat pontosan egy meccset játszik, mert $A_m$ ellenfele $K$, ha pedig $i\ne m$, akkor az $A_i$ pont $A_{m}K$ egyenesre vonatkozó tükörképe a sokszög egy $A_j\ne A_i$ csúcsa (itt használjuk ki, hogy a sokszögnek páratlan sok csúcsa van), s az ennek megfelelő csapattal játszik $A_i$. Az is látszik, hogy bármely két csapat pontosan egyszer találkozik a bajnokság során. Ez $K$ esetén nyilvánvaló, $A_i$ és $A_j$ esetén pedig abból következik, hogy az $A_i{A}_j$ szakasz felezőmerőlegese átmegy $K$-n és a sokszögnek pontosan egy $A_m$ csúcsát tartalmazza, a meccsre az ennek megfelelő ${\text{F}}_m$ fordulóban kerül sor.   A kétféle bajnokságszervezés leírása alig tér el egymástól. Ez nem véletlen, azért van így, mert a véges síkok parabolái és az euklidészi sík körei sok szempontból ugyanolyan görbék. Az azonban, hogy mit értünk ezen, már egy következő cikk témája.   Irodalom   [1] Bérczi Gergely, Gács András, Hraskó András és Szőnyi Tamás: Reguláris gráfok, Új matematikai mozaik (szerk. Hraskó András), Typotex Kiadó, Budapest, 2002, 77‐104. [2] Freud Róbert: Lineáris algebra, ELTE Eötvös Kiadó, Budapest, 1998. [3] Kárteszi Ferenc: Bevezetés a véges geometriákba, Akadémiai Kiadó, Budapest, 1972. [4] Kiss György és Szőnyi Tamás: Véges geometriák, Polygon Kiadó, Szeged, 2001. [5] Montágh Balázs: Salakmotor versenyek és véges síkok, Új matematikai mozaik (szerk. Hraskó András), Typotex Kiadó, Budapest, 2002, 7‐52. [6] Wallis, W. D.: One-Factorizations, Kluwer Academic Publishers, Dordrecht, 1997. 1A cikk elklészítését a Nemzeti Kutatási és Technológiai Hivatal (NKTH) támogatta az Öveges József program keretében. A támogatás forrása a Kutatási és Technológiai Innovációs Alap.