Cím:	A 2005-2006. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2006/november, 454 - 459. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. KEZDŐK   Első forduló   Mindhárom kategória   1. Aladár és Béla együtt ünnepli születésnapját 2006-ban. Aladár pontosan kétszer annyi idős, mint Béla. Aladár születési évének utolsó két számjegyét felcserélve éppen Béla születési évét kapjuk. Mennyi idősek most? (6 pont)   2. Rest Elek nem készült a dolgozatra, de tudta, hogy ugyanazokat a feladatokat szokták kapni, mint a párhuzamos osztály, legfeljebb más sorrendben. Megtudta, hogy a párhuzamos osztályban A, C, D, B voltak a helyes válaszok. Így ő is ezt írta le valamilyen sorrendben. Mennyi annak a valószínűsége, hogy $a)$ nem lesz jó válasza; $b)$ pontosan 1 jó válasza lesz; $c)$ pontosan 2 jó válasza lesz; $d)$ pontosan 3 jó válasza lesz; $e)$ mind a négy válasza jó lesz? (6 pont)   3. Hányféleképpen lehet (a tízes számrendszerben) a 2006-ot legalább két egymást követő pozitív egész szám összegeként felírni? (8 pont)   4. Az $ABCD$ derékszögű trapézban $AB$ párhuzamos $CD$-vel, $AD$ merőleges $AB$-re és $AB=AD=2CD$. Jelölje $M$ az $AC$ és $BD$ átlók metszéspontját, és $F$ az $AD$ oldal felezőpontját! Bizonyítsa be, hogy $MF$ merőleges $BC$-re! (10 pont)   5. Oldja meg a $\begin{array}{c}{\displaystyle p^q+q^p=r}\end{array}$ egyenletet, ha $p$, $q$, $r$ pozitív prímszámok! (10 pont)   Második (döntő) forduló   I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   1. Igazolja, hogy $9^n+8^n+7^n+6^n-4^n-3^n-2^n-1^n$ bármely $n$ természetes szám esetén osztható 10-zel!   2. Adott egy hegyesszög tartomány belsejében a $P$ pont. Szerkesszen $P$-n át olyan egyenest, amely mind a két szögszárat metszi és a szögtartományból a legkisebb területű háromszöget metszi ki!   3. Igazolja, hogy ha az $x$ valós számra $3\le x\le 16$, akkor: $\begin{array}{c}{\displaystyle \sqrt[]{x+5}+\sqrt[]{2x-6}+\sqrt[]{49-3x}\le 12.}\end{array}$   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   1. Le lehet-e ültetni egy kerek asztal köré hat olyan embert, akik közül mindenkinek pontosan két haragosa van (a harag kölcsönös) úgy, hogy senki ne üljön haragosa mellett?   2. Egy 4 dm élű kocka mindegyik csúcsát levágtuk olyan síkkal, amely a csúcsból induló élek felezőpontjaira illeszkedik. Az így kapott testtel ugyanígy jártunk el. Mennyi a most keletkezett test felszíne?   3. Tekintsük azokat a 9-jegyű számokat, amelyek az $\mathrm{1,2,}\text{...}\mathrm{,9}$ számjegyekből képezhetők úgy, hogy minden számjegy pontosan egyszer szerepel. Rendezzük ezeket növekvő sorba, majd vegyük a szomszédos számok különbségét! Melyek azok a számok, amelyek a kapott számok között páratlan sokszor szerepelnek?   III. kategória: Speciális tantervű osztályokban tanulók   1. Aladár és Béla a következő játékot játsszák. Felváltva mondanak egy-egy pozitív egész számot, azzal a megkötéssel, hogy a kimondott szám mindig kisebb, de legalább fele akkora legyen, mint az előzőleg elhangzott szám. Az győz, aki először mondja ki az 1-et. Aladár a 2006-os számmal kezdi a játékot. Mit kell erre mondania Bélának, ha azt akarja, hogy biztosan nyerjen?   2. Adott egy egységsugarú kör. Tekintsük azokat a körbe írható 2006-szögeket, melyek belsejükben tartalmazzák a kör középpontját. Bizonyítsuk be, hogy minden ilyen sokszög kerülete nagyobb, mint 4 egység!   3. Igazolja, hogy ha a $p$ és a $q$ pozitív egész számokra fennáll a $p^{q^p}=q^{p^q}$ egyenlőség, akkor $p=q$.   HALADÓK   I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. Hány olyan egész számokból álló $\left(x;y\right)$ számpár van, amelyre $\frac{1}{x}+\frac{1}{y}=\frac{1}{2005}$ teljesül?   2. A szultán kastélya egy négyzet alakú területen épült, és félhold alakú tó veszi körül, az ábrán látható módon. 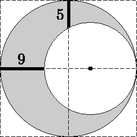    A tavon két híd vezet át, melyek egyenese átmegy a négyzet középpontján. A hidak hossza 5 és 9 méter. Mekkora a négyzet alakú terület?   3. Ha $x<-1$, akkor mi az $\begin{array}{c}{\displaystyle \left|x^{-1}-\frac{{\left(\frac{1}{x+1}-\frac{1}{x}\right)}^2}{\frac{1}{x}-\frac{1}{x+1}}-{\left(\frac{1}{1-x}\right)}^{-1}\right|}\end{array}$ kifejezés legkisebb értéke?   4. Az $ABC$ háromszögben $A{A}_1$, $B{B}_1$, $C{C}_1$ magasságok, $A{A}_2$, $B{B}_2$, $C{C}_2$ súlyvonalak. Bizonyítsuk be, hogy az $A_2{B}_1{C}_2{A}_1{B}_2{C}_1{A}_2$ töröttvonal hossza az $ABC$ háromszög kerületével egyenlő!   5. Határozza meg azokat az egész számokból álló $\left(x;y\right)$ számpárokat, amelyek kielégítik a következő egyenletet: $\begin{array}{c}{\displaystyle {\left(x+2\right)}^4-x^4=y^3\mathrm{.}}\end{array}$   Második forduló   1. Oldjuk meg az egész számok halmazán a ${\left(\sqrt[]{2}-1\right)}^6=\sqrt[]{m}-\sqrt[]{m-1}$ egyenletet!   2. Igazoljuk, hogy ha egy derékszögű háromszög súlyvonalaiból ‐ mint oldalakból ‐ derékszögű háromszög szerkeszthető, akkor a szerkesztett háromszög hasonló az eredeti háromszöghöz.   3. Milyen $n$ pozitív egész esetén oldható meg az alábbi egyenletrendszer: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}{\displaystyle x+y+z=1}\hfill \\ {\displaystyle xyz=2^n}\hfill \end{array}}\text{ha}x\mathrm{,}y\mathrm{,}z\in \text{Z}?}\end{array}$   4. Válasszunk ki egy kocka csúcsai közül az összes lehetséges módon hármat, és tekintsük a csúcsok által meghatározott háromszögeket! Mekkora a kapott derékszögű háromszögek számának és az összes háromszög számának aránya?   Harmadik (döntő) forduló   1. Oldja meg a következő egyenletrendszert a valós számok halmazán! $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}{\displaystyle \text{I.}}\hfill & \hfill {\displaystyle {\left(x+y\right)}^3}& {\displaystyle =z\mathrm{,}}\hfill \\ {\displaystyle \text{II.}}\hfill & \hfill {\displaystyle {\left(y+z\right)}^3}& {\displaystyle =x\mathrm{,}}\hfill \\ {\displaystyle \text{III.}}\hfill & \hfill {\displaystyle {\left(z+x\right)}^3}& {\displaystyle =y\mathrm{.}}\hfill \end{array}}}\end{array}$   2. Az $AB$ szakasz egy belső pontja $C$, amire $AC>CB$. Az $AB$ és $BC$ szakaszok, mint átmérő fölé ($AB$ azonos oldalán) félköröket rajzolunk, legyenek ezek rendre $k_1$ és $k_2$. Az $AB$-re $C$-ben állított merőleges $m$. A $k$ kör érinti az $m$ egyenest, a $k_2$ félkört kívülről, a $k_1$ félkört pedig belülről. Legyen $k$ középpontja $O$, és jelölje $k$ és $k_2$ érintési pontját $E$. Végül az $OE$ egyenes és $m$ metszéspontja $M$. Mutassuk meg, hogy $AC=EM$!   3. Nevezzünk egy halmazt csonkának, ha nincs két ‐ nem feltétlenül különböző ‐ elem a halmazban, aminek az összege is eleme a halmaznak. Mekkora az $\left\{\mathrm{1,2,3,}\text{...}\mathrm{,}2n+1\right\}$ halmaz maximális elemszámú csonka részhalmaza?   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló   1. Az $a$ és $b$ valós számra $a^2+b^2=1$ teljesül, ahol $ab\ne 0$. Határozzuk meg az $\begin{array}{c}{\displaystyle \left(1+\frac{1}{a^2}\right)\left(1+\frac{1}{b^2}\right)}\end{array}$ szorzat minimumát.   2. Az $AB$ alapú egyenlő szárú háromszög alapjának felezőpontja $F$, súlypontja $S$, magasságpontja $M$, beírt köre $k$. Ha $FM=\sqrt[]{6}$ és $S$ illeszkedik $k$-ra, akkor mekkora a háromszög kerülete?   3. A Piramis Bank elnöke a külvárosból jár be munkahelyére dolgozni. Hétköznapokon egy sofőr jön érte, aki minden nap ugyanabban az időpontban indul a banktól, felveszi az elnököt, és pontosan nyitásra megérkeznek. Egyik reggel a sofőr telefonált, hogy valami baj van az autóval, ezért valószínűleg késni fog. Az elnök emiatt a szokottnál egy órával korábban, gyalog indult munkába. A sofőr közben megjavította az autót, és mégis el tudott indulni a szokásos időpontban, így útközben találkozott a bankárral. Felvette, és nyitás előtt 20 perccel érkeztek a bankhoz. Mennyi ideig sétált a bankár? (Feltehetjük, hogy az autó sebessége állandó és az utas felvétele nem jár időveszteséggel.)   4. Egy $ABC$ hegyesszögű háromszög belsejében egy tetszőleges $O$ pontból merőlegeseket bocsátunk az $AB$, $BC$ és $CA$ oldalakra. A talppontokat rendre jelöljük $R$-rel, $P$-vel és $Q$-val. Rajzoljunk kifelé négyzeteket az $RB$-re, $PC$-re és $AQ$-ra. Mekkora a három négyzet területének összege, ha tudjuk, hogy $AR=7$, $BP=5$ és $CQ=6?$   5. Határozza meg azokat az egész számokból álló $\left(x;y\right)$ számpárokat, amelyek kielégítik a következő egyenletet: $\begin{array}{c}{\displaystyle {\left(x+2\right)}^4-x^4=y^3\mathrm{.}}\end{array}$   Második forduló   1. Határozza meg az $a$, $b$, $c$ egészek értékét úgy, hogy a következő egyenlőség minden valós $x$-re teljesüljön: $\begin{array}{c}{\displaystyle \left(x-a\right)\cdot \left(x-10\right)+1=\left(x+b\right)\cdot \left(x+c\right)\mathrm{.}}\end{array}$   2. A $t$ területű, $m$ magasságú $ABCD$ húrtrapéz alapjai $AB$ és $CD$, az átlók metszéspontja $M$, a trapéz körülírt körének középpontja $O$. A $BC$ oldal felezőpontja $E$, az $AD$ oldalé pedig $F$. Bizonyítsuk be, hogy ha $t=m^2$, akkor az $OEMF$ négyszög rombusz.   3. Határozzuk meg a valós számok halmazán értelmezett $f\left(x\right)=\frac{x^2-1}{x^2+3x+4}$ függvény legkisebb és legnagyobb értékét!   4. Az $\left(a_n\right)$ számsorozatot a következő módon határozzuk meg: $a_1=a$, ahol az ,,$a$'' szám pozitív egész szám, $n\ge 1$ esetén pedig $\begin{array}{c}{\displaystyle a_{n+1}=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{1}{2}{a}_n\mathrm{,}}& {\displaystyle \text{ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mi>n</mi></mrow></msub></mrow></math> páros szám,}}\hfill \\ \hfill {\displaystyle 2a_n+\mathrm{2,}}& {\displaystyle \text{ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mi>n</mi></mrow></msub></mrow></math> páratlan szám.}}\hfill \end{array}}}\end{array}$ Bizonyítsuk be, hogy $a=2^{2006}+5$ esetén a sorozatnak tagja az 1, 2, 3, 4, 5 számok mindegyike.   Harmadik (döntő) forduló   1. Egy négyzet egyik oldalára az ábrán látható módon három kisebb négyzetet rajzoltunk. Kössük össze a nagy és a középső kis négyzet középpontját, valamint a két szélső négyzet középpontját. Bizonyítsa be, hogy ezek a szakaszok derékszöget zárnak be!     2. Milyen $n$ természetes számra igaz, hogy a $4^{2005}+4^{2006}+4^n$ összeg értéke négyzetszám?   3. Egy különleges számológép legfeljebb 10-jegyű nemnegatív egész számokkal tud dolgozni. Két művelet van a gépen. Az ``N'' művelet négyzetre emel, a ``T'' művelet pedig levágja a szám utolsó (egyesek helyén álló) jegyét, ha a szám legalább kétjegyű. Egy alkalommal valaki egy legfeljebb háromjegyű számból kiindulva, több művelet végrehajtása után, a 2 számot kapta eredményül. Mi lehetett az eredeti szám?   III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló   1. Oldjuk meg az egész számok halmazán a következő egyenletrendszert: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle x^2}& {\displaystyle =y^2+z^2+\mathrm{1,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle x}& {\displaystyle =y+z-3.}\hfill & \text{(<mn>2</mn>)}\end{array}}$   2. Az $AB$ szakasz $A$ csúcshoz közelebbi harmadolópontja $H$. Az $AHC$ és $HBD$ szabályos háromszögek az $AB$ egyenes azonos oldalán helyezkednek el. $AD$ és $HC$ metszéspontja $P$, $BC$ és $HD$ metszéspontja $Q$, $AD$ és $BC$ metszéspontja $M$. Határozzuk meg a $PQ:AB$ arány értékét, és bizonyítsuk be, hogy az $M$, $P$, $H$, $Q$ pontok egy körön vannak.   3. Legyen $x$ tetszőleges pozitív egész szám, és jelölje $f\left(x\right)$ az $x$ szám és $x$ számjegyei összegének különbségét, ahol $f\left(x\right)=0$, ha az $x$ szám egyjegyű. Oldjuk meg az $f\left(f\left(f\left(x\right)\right)\right)=9$ egyenletet!   4. Bizonyítsuk be, hogy a $\begin{array}{c}{\displaystyle {\left(\sqrt[]{2}-1\right)}^{2006}=\sqrt[]{m}-\sqrt[]{m-1}}\end{array}$ egyenlet megoldható a pozitív egész számok halmazán!   5. Adott $2n+3$ pont a síkon úgy, hogy nincs 3 egy egyenesen, és nincs 4 egy körön. Bizonyítsa be, hogy mindig létezik egy $k$ kör, ami pontosan 3 ponton megy keresztül, és $n$ pont van a kör belsejében és $n$ a körön kívül!   Második (döntő) forduló   1. Az $AB$ átfogójú derékszögű háromszögben $AC>BC$. A háromszög köréírt körét a $C$ csúcsból induló magasságvonal az $E$, míg a $C$-ből induló belső szögfelező a $D$ pontban metszi. Bizonyítsuk be, hogy a $BCDE$ négyszög területe megegyezik az $ABC$ háromszög területével.   2. Definiáljuk az $x_i$ sorozatot a következőképpen: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle x_1}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle x_{k+1}}& {\displaystyle =x_k^2+x_k\mathrm{,}k\ge \mathrm{1,}k\in \text{Z}\mathrm{.}}\hfill \end{array}}}\end{array}$ Bizonyítsuk be, hogy az $\begin{array}{c}{\displaystyle S=\frac{1}{1+x_1}+\frac{1}{1+x_2}+\frac{1}{1+x_3}+\text{...}+\frac{1}{1+x_{2006}}}\end{array}$ összeg 1-nél kisebb!   3. Bizonyítsuk be, hogy az egységnyi oldalú $ABCD$ négyzet belsejében végtelen sok olyan $P$ pont van, amelyre igaz, hogy a $\frac{PB}{PA}$, $\frac{PC}{PA}$, $\frac{PD}{PA}$ arányok mindegyike racionális szám.