Cím:	IX. Román-magyar előolimpiai fizikaverseny
Füzet:	2006/szeptember, 375 - 378. oldal	PDF  |  MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1   (Budapest, 2006. június 6‐10.)     1. feladat (amely három független részből áll).   1/A. Folyadékcsepp tömege (3 pont) Egy asztallapon folyadékcsepp ,,fekszik''. A folyadék felületi feszültsége $\alpha$, sűrűsége $\varrho$. A csepp magassága $h$, legmagasabb pontjánál a felület görbületi sugara $R$. A csepp az asztallal $r$ sugarú kör mentén érintkezik, és az ,,érintkezési szög'' $\varth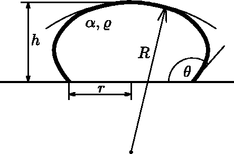eta$ (1. ábra).     1. ábra   Mekkora a csepp tömege?   1/B. Henger mozgása lejtőn (4 pont) $\alpha ={30}^{\circ }$-os hajlásszögű, hosszú lejtőn $l=30$ cm hosszúságú, érdes felületű papírlap közepén tömör, homogén anyageloszlású henger fekszik (2. ábra). Az elengedést követően a papírlapot úgy húzzuk felfelé, hogy a henger tömegközéppontja mozdulatlan marad. (A henger a papírlapon nem csúszik meg.) A henger és a lejtő között a tapadási és a csúszási súrlódási együttható megegyezik, értéke 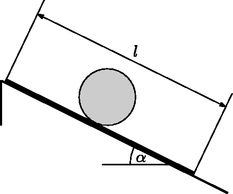$\mu =0\mathrm{,}3$.     2. ábra   Ábrázoljuk közös grafikonon a papírlap sebességét és a henger tömegközéppontjának sebességét az idő függvényében! A grafikonon numerikusan jelöljük be a jellemző idő- és sebesség-értékeket!   1/C. Politrop folyamatok (3 pont) Bizonyos mennyiségű egyatomos ideális gáz nyomása az $A$ jelű kezdőállapotban $p_A$, térfogata $V_A$. A gázzal a következő körfolyamatot végeztetjük: $\left(A\right)\to \left(B\right)$: Összenyomjuk $V_B=V_A/4$ térfogatra úgy, hogy a nyomása nem változik meg. $\left(B\right)\to \left(C\right)$: Politropikus állapotváltozással (vagyis amikor $p{V}^n=$ állandó, ahol $n$ konstans) eljuttatjuk a $p_C=8p_A$, $V_C=V_A/8$ állapotba. $\left(C\right)\to \left(D\right)$: Izobár módon kitágítjuk $V_D=V_A/4$ térfogatra. $\left(D\right)\to \left(A\right)$: Végül politrop módon visszajuttatjuk a kezdőállapotba.   $a)$ Mekkora az egyes részfolyamatokhoz tartozó politrop kitevő? $b)$ Mekkora a gáz mólhője az egyes részfolyamatokban? $c)$ Melyik részfolyamatban történik hőfelvétel és melyikben ad le hőt a gáz?   2. feladat. Űrszonda a Napba? (10 pont) Egy űrszondát a Merkur gravitációs terének (az ún. parittya-hatásának) kihasználásával szeretnénk a Napba (a Nap közvetlen közelébe) juttatni. A szondát a Föld közvetlen közelében rövid ideig működő rakétával gyorsítjuk fel a Föld felszínéhez képest $v_0$ nagyságú, a további mozgás szempontjából legalkalmasabb irányú sebességre. (Ezután további, hajtóművel történő pályamódosításra már nincs lehetőség, mert a rakéta minden üzemanyagát elhasználta.) Az űrszonda ,,elhagyja'' a Föld gravitációs terét, és bizonyos idő múlva eljut a Merkur közelébe. Itt a bolygó gravitációs terének hatására az űrszonda sebessége megváltozik, és a Merkur gravitációs terét elhagyva a Napba zuhanhat. A szonda mozgásának elemzésekor felhasználhatjuk a következő közelítést: Amíg a szonda valamelyik égitest (a Föld, a Merkur stb.) közelében tartózkodik, elegendő csak annak az égitestnek a gravitációs hatásával számolni, a többi bolygó és a Nap gravitációs terétől eltekinthetünk. A bolygóktól ,,kellően'' eltávolodott szondánál viszont a bolygók gravitációs terét figyelmen kívül hagyhatjuk, és a szonda mozgását egyedül a Nap gravitációs vonzóerejéből számíthatjuk. Feltételezhetjük továbbá, hogy a szonda olyan ellipszispályán mozog, amely mind a Föld, mind pedig a Merkur pályáját érinti. A Föld és a Merkur pályáját azonos síkban fekvő körnek tekinthetjük, és az egyszerűség kedvéért a Föld forgástengelyének irányát vegyük erre a síkra merőlegesnek! Adatok: A Föld egyenlítői sugara: $R_F=6380\text{km}$. A gravitációs állandó: $G=6\mathrm{,}67\cdot {10}^{-11}\text{N <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>/k<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>g</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$. A Föld tömege: $M_F=5\mathrm{,}97\cdot {10}^{24}\text{kg}$. A Nap tömege: $M_N=1\mathrm{,}98\cdot {10}^{30}\text{kg}$. A Föld közepes pályasugara: $r_F=1\mathrm{,}50\cdot {10}^{11}\text{m}$. A Merkur közepes pályasugara: $r_M=5\mathrm{,}79\cdot {10}^{10}\text{m}$. A Merkur keringési ideje: $T_M=88$ (földi) nap. $a)$ A Föld mely pontjai a legkedvezőbbek az űrszonda indítására, és milyen földrajzi irányba célszerű indítani a rakétát? $b)$ Mekkora a szonda $v_1$ sebessége a Föld tömegközéppontjához képest a rakétahajtóművel történő gyorsítás végén? A választ a $v_0$ indítási sebesség és a többi adat segítségével adjuk meg! $c)$ A Földhöz képest mekkora $v_2$ sebességgel mozog a szonda, amikor elhagyja a Föld gravitációs terét? A választ a $v_1$ sebesség és a többi adat segítségével adjuk meg! $d)$ A Naphoz képest mekkora $v_3$ sebességgel mozog a szonda, amikor éppen elhagyta a Föld gravitációs terét? A választ a $v_2$ sebesség és a többi adat segítségével adjuk meg! $e)$ A Naphoz képest mekkora $v_4$ sebességgel mozog a szonda, amikor már viszonylag közel van a Merkur bolygóhoz, de az még nem befolyásolta jelentősen a szonda mozgását? A választ a feladat paramétereivel is és numerikusan is adjuk meg! Adjuk meg a szondának a Merkurhoz viszonyított $\Delta v$ sebességét is numerikusan! $f)$ A  szonda a Merkur gravitációs terében irányt változtat, és ha a Merkurhoz viszonyított sebessége elegendően nagy, akkor a bolygóval való ,,ütközése'' után a Napba zuhanhat. Teljesül-e ez a feltétel, azaz megvalósítható-e a program a leírt módon?   3. feladat. Stern‐Gerlach-kísérlet a klasszikus fizika szemszögéből (10 pont) Stern és Gerlach az atomok elektronoktól származó mágneses momentumát vizsgálta úgy, hogy atomokból álló részecskenyalábot lőtt inhomogén mágneses térbe, és a nyaláb eltérülését vizsgálta. A részecskenyaláb több, különböző szögben eltérülő, egymástól jól elkülöníthető nyalábra oszlott. Ez a kísérleti tény igazolta, hogy az atomban kötött elektronok impulzusmontuma, és így mágneses momentuma is kvantált. A kísérlet alkalmas az elektron saját mágneses momentumának, spinjének kimutatására, és a különböző spinbeállású elektronok szétválasztására is. Vizsgáljuk meg, hogy milyen mélységben érthető meg a jelenség pusztán klasszikus fogalmak felhasználásával! Az egyszerűség kedvéért tekintsünk szabad (nem atomban kötött) elektront. Az elektront tekintsük $m$ tömegű, $-e$ töltésű, $r$ sugarú, térfogatában egyenletesen töltött kis gömbnek, mely $\text{v}$ sebességgel halad, és $\overrightarrow{\omega }$ szögsebességgel forog. Hozzunk létre a tér egy $0<x<d$ tartományában inhomogén mágneses teret, melyet az elektronok pályája mentén a $\begin{array}{c}{\displaystyle \text{B}\left(\text{r}\right)=\left[{\displaystyle \begin{array}{c}\hfill {\displaystyle B_x\left(x\mathrm{,}y\mathrm{,}z\right)}\hfill \\ \hfill {\displaystyle B_y\left(x\mathrm{,}y\mathrm{,}z\right)}\hfill \\ \hfill {\displaystyle B_z\left(x\mathrm{,}y\mathrm{,}z\right)}\hfill \end{array}}\right]=\left[{\displaystyle \begin{array}{c}\hfill {\displaystyle 0}\hfill \\ \hfill {\displaystyle \alpha z}\hfill \\ \hfill {\displaystyle B_0+\alpha y}\hfill \end{array}}\right]\mathrm{,}\text{ha}0<x<d}\end{array}$ formula jellemez, és lőjük át ezen a térrészen a ,,klasszikus'' elektront az $x$ tengely mentén $\text{v}$ sebességgel és $\overrightarrow{\omega }$ szögsebességgel, ahol $\begin{array}{c}{\displaystyle \text{v}=\left[{\displaystyle \begin{array}{c}\hfill {\displaystyle v}\hfill \\ \hfill {\displaystyle 0}\hfill \\ \hfill {\displaystyle 0}\hfill \end{array}}\right]\mathrm{,}\overrightarrow{\omega }=\pm \left[{\displaystyle \begin{array}{c}\hfill {\displaystyle 0}\hfill \\ \hfill {\displaystyle 0}\hfill \\ \hfill {\displaystyle \omega }\hfill \end{array}}\right]\mathrm{.}}\end{array}$ A megoldás során feltételezhetjük, hogy az elektronok szögeltérülése kicsiny, és alkalmazhatunk ennek megfelelő közelítéseket. $a)$ Milyen irányban és mekkora szöggel térülnének el az elektronok, ha nem forognának? Az eredményt fejezzük ki az elektron $I$ impulzusával és töltésével, valamint a mágneses tér jellemzőivel! $b)$ Mekkora erő hat a forgó elektronnak a középpontjától $\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\text{'}$ vektorral megadott helyen levő, kicsiny $\Delta V$ térfogatú darabkájára? $c)$ Milyen irányban (melyik koordinátatengely mentén) válik szét a kétféle forgásirányú elektronokból álló nyaláb? $d)$ Határozzuk meg a pozitív, illetve negatív irányban forgó elektronok szétválásának szögét! Eredményünket fejezzük ki az elektron $I$ impulzusával és $N$ impulzusmomentumával, töltésével, valamint a mágneses tér jellemzőivel! 1A versenyen egy kísérleti és három elméleti feladat szerepelt; itt most ‐ terjedelmi okokból ‐ az elméleti problémákat ismertetjük.