Cím:	A lyukas dob hangjai
Szerző(k):	Hagymási Imre
Füzet:	2008/május, 301 - 305. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek, Egyéb hullámfajták

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1   Bevezetés   A membránok (vékony, hajlékony, elhanyagolható tömegű, megfeszített hártyák, pl. egy dob hártyája, vagy szappanhártya) rezgéseinek leírása már régóta foglalkoztatja a fizikusokat. Különösen a téglalap és kör alakú membránokat vizsgálták részletesen a szakirodalomban. A membránok és vékony lemezek rezgésének tanulmányozása több mint 200 évvel korábbra, egészen Ernest Friedrich Florens Chladni munkásságáig nyúlik vissza, aki különböző alakú lemezeken kialakuló csomóvonalakat tanulmányozott. Erről írt Cserti József a KöMaL 2004. évi áprilisi számában A Chladni-féle porábráktól a nanofizikáig címmel. A rugalmasságtan elméleti alapjainak kidolgozása után megnyugtatóan tisztázódtak a membránok, lemezek és a 3 dimenzióban kiterjedt rugalmas testek rezgéseit megadó elvi kérdések, bár még ma is igen nehéz feladat a rezgési mintázatok és a hozzájuk tartozó frekvenciák, az ún. sajátfrekvenciák megadása egy tetszőleges alakú membrán esetén. Mint említettük, a kör alakú membrán rezgése megoldott probléma, ismertek a sajátfrekvenciái. Természetesen vetődhet fel a kérdés: hogyan változik meg egy dob (membrán) hangja, ha kilyukasztjuk középen? Ezen kérdés megválaszolásához egy koncentrikusan lyukas membrán sajátrezgéseit vizsgáltuk, azzal a határfeltétellel, hogy a külső perem rögzített, míg a belső határvonal szabadon elmozdulhat. A dobok esetében a szabadon mozgó lyuk fizikailag úgy valósítható meg, hogy a hártyára nyújthatatlan, de könnyen hajló fonálból zárt hurkot erősítünk, majd a hártyának a hurkon belüli részét eltávolítjuk. Meglepő, hogy ezt a problémát (ezekkel a határfeltételekkel) mindeddig még nem vizsgálták, legalábbis nincs rá utalás a szakirodalomban. Igen érdekes, hogy a fentebb kitűzött feladattal egy másik ‐ az alkalmazások szempontjából talán jelentősebb ‐ problémát is megoldunk. A mai félvezetőiparban már elő tudnak állítani néhány 100 nanométer méretű mintákat, amelyekben az elektronok mozgását kisméretű, kétdimenziós tartományokra lehet korlátozni. Ilyen kétdimenziós tartomány jön létre például GaAs és AlGaAs félvezető rétegek összeillesztésénél. Egy ilyen kisméretű síkbeli tartományban ‐ esetünkben egy kilyukasztott körlapon ‐ mozgó elektron leírása csak a kvantummechanika segítségével lehetséges. Az ilyen rendszerek viselkedésének megértése elengedhetetlen pl. a ,,nanotranzisztorok'' létrehozásához. A továbbiakban megpróbáljuk illusztrálni, hogy a fent említett két terület hogyan is kapcsolódik össze és miképpen válnak a membránok rezgéséről megszerzett ismereteink a kvantumfizikában is hasznosítható tudássá.   Membránok rezgései   Egy membrán $u\left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\mathrm{,}t\right)$ kitérés-idő függvényét egy bonyolult differenciálegyenlet írja le. Ha a problémának egy adott $\omega$ frekvenciájú, harmonikus rezgőmozgást leíró (ún. monokromatikus) megoldását keressük, akkor egy kicsit egyszerűbb egyenlethez, az ún. Helmholtz-egyenlethez jutunk. Ez az egyenlet határozza meg, hogy melyek a membrán lehetséges rezgési frekvenciái, mik a sajátfrekvenciái. Általában minden sajátfrekvenciához tartozik a membránnak egy jellegzetes ,,rezgési alakja'', ezt nevezzük sajátmódusnak. Középiskolából is jól ismert, hogy egy egydimenziós rezgő rendszer, a mindkét végén rögzített húr sajátfrekvenciái egy bizonyos (a húr hosszától függő) alapfrekvenciáknak egész számú többszörösei. Téglalap vagy kör alakú membránnál ez már nem igaz, a sajátfrekvenciák bonyolultabb rend szerint követik egymást. Téglalap esetében zárt alakban megadható egy formula a sajátfrekvenciákra, de kör esetében már ez sem igaz. Elvben tetszőleges alakú membránnak egyértelműen kiszámíthatók a sajátfrekvenciái és sajátmódusai, amennyiben megadjuk, hogy a membrán szélei rögzítettek vagy sem. Általában ez igen nehéz matematikai feladat, főleg ha a vizsgált rendszer nem rendelkezik semmilyen szimmetriával. Feltehető a fordított kérdés is: vajon hallható-e egy dob alakja, vagyis ha ismerjük a dob valamennyi sajátfrekvenciáját, meg tudjuk-e határozni ebből a dob alakját? Ezt a kérdést ilyen formában Mark Kac vetette fel 1966-ban, de a probléma sokkal régebbre nyúlik vissza, Hermann Weyl, a híres matematikus is foglalkozott vele 1911-ben. A kérdés egészen 1991-ig nyitott maradt, amikor találtak két olyan különböző alakú membránt, amelyek frekvenciaspektruma (sajátfrekvenciáinak rendszere) megegyezett. Egy kör alakú membrán esetén elvileg egyértelműen meghatározottak a sajátfrekvenciák és a rezgési módusok. Ez igaz marad akkor is, ha a középen lyukas membránt tekintjük. A sajátfrekvenciákat azonban ‐ mindkét esetben ‐ csak numerikus módszerek segítségével lehet kiszámolni. Jelöljük a lyuk sugarát $R_1$-gyel, a membránét pedig $R_2$-vel, és vezessük be a $\begin{array}{c}{\displaystyle \lambda =\frac{R_1}{R_2}}\end{array}$ (1) dimenziótlan paramétert! A táblázatban feltüntettük, hogy a lyuk sugarától függően hogyan változik a dob első sajátfrekvenciája ahhoz képest, mintha nem lenne lyuk rajta. A hátsó borítón pedig az eddig említett membránok első néhány sajátmódusát ábrázoltuk.   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>λ</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>1</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>2</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>3</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>5</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>9</mn></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Δ</mi><mi>ω</mi><mo stretchy="false">/</mo><mi>ω</mi></math>}}\hfill & \hfill {\displaystyle \text{0,01}}\hfill & \hfill {\displaystyle \text{0,07}}\hfill & \hfill {\displaystyle \text{0,15}}\hfill & \hfill {\displaystyle \text{0,49}}\hfill & \hfill {\displaystyle \text{5,67}}\hfill \\ \hline\end{array}}$   Az alapfrekvencia relatív megváltozása a lyuk sugarának néhány értékénél   Fizikailag érezzük, hogy minél nagyobb a lyuk sugara, annál nagyobbak a sajátfrekvenciák. A rendszer részletesebb analízisével kimutatható, hogy a sajátfrekvenciák a következőképpen függnek a lyuk méretétől: $\begin{array}{c}{\displaystyle {\omega }_n\sim \frac{1}{1-\lambda }\mathrm{,}}\end{array}$ (2) vagyis a lyuk sugarát növelve a sajátfrekvenciák hiperbola ágak mentén tartanak a végtelenhez.   Alkalmazás a kvantummechanikában   Ma már egyértelműen bizonyítottnak tekinthető, hogy a mikrorészecskék hullámtermészettel rendelkeznek; ezt számos kísérleti tény támasztja alá. Egy kvantummechanikai rendszerről minden információt tartalmaz a rendszer $\Psi \left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\mathrm{,}t\right)$ hullámfüggvénye. Egyetlen mikrorészecske esetén például a részecske megtalálási valószínűsége az $\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}$ pontban és $t$ időpillanatban arányos a hullámfüggvény abszolút értékének négyzetével, $|\Psi \left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\mathrm{,}t\right){|}^2$-tel. A $\Psi \left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\mathrm{,}t\right)$ függvény kielégíti az ún. Schrödinger-egyenletet. Ez egy bonyolult, többváltozós függvényre vonatkozó differenciálegyenlet, amelynek ‐ bizonyos határfeltételekhez tartozó ‐ megoldása megadja a részecske hullámfüggvényét. Már a kvantummechanika törvényeinek részletes ismerete előtt ismert volt a hidrogénatom vonalas színképe, ezt és a hidrogénatom állapotának további részleteit később a Schrödinger-egyenlet is nagy pontossággal igazolta. Az atomokban az elektronok csak bizonyos energiájú szinteken ,,tartózkodhatnak'', és általánosabban is igaz, hogy egy kötött állapotban levő részecske energiaszintjei a Schrödinger-egyenlet szerint diszkrét (egymástól élesen elkülönülő) spektrumot alkotnak. A membrán $u\left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\mathrm{,}t\right)$ kitérésfüggvényét leíró egyenlet és egy szabad részecske $\Psi \left(\text{<span style="font-weight: bold;"><span style="font-style: italic;">r</span></span>}\mathrm{,}t\right)$ hullámfüggvényét meghatározó egyenlet egyaránt a Helmholtz-egyenlet (feltéve, hogy a membrán egy meghatározott sajátfekvencián rezeg, illetve a részecske egy meghatározott energiájú állapotban, ún. sajátállapotban van). Belátható, hogy a membrán sajátfrekvenciáit megfeleltethetjük a részecske energiaszintjeinek az alábbi formula szerint: $\begin{array}{c}{\displaystyle E_n=\frac{{\hslash }^2{k}_n^2}{2m}\left(\hslash =\frac{h}{2\pi }\right)\mathrm{,}}\end{array}$ (3) ahol $k_n=\frac{{\omega }_n}{c}$, ${\omega }_n$ a membrán $n$-edik sajátfekvenciája, $c$ pedig a hullám terjedési sebessége a membránban. Egy igen kicsiny (atomi méretű) kétdimenziós tartományt, amelynek a faláról klasszikus fogalmaink szerint visszaverődik a részecske, kvantum-biliárdnak nevezünk. Jelen esetben a lyukas membrán sajátrezgései az atomi világban annak feleltethető meg, hogy egy mikrorészecske egy lyukas körlap alakú ,,biliárdasztalon'' mozog. Azt állíthatjuk, hogy egy kilyukasztott kör alakú tartományba zárt részecske megengedett energiaszintjei megfeleltethetők a lyukas dob sajátfrekvenciáinak a (3) formulának megfelelően. Még egy fogalmat érdemes megemlítenünk: az energiaszintek állapotsűrűségét. Jelölje 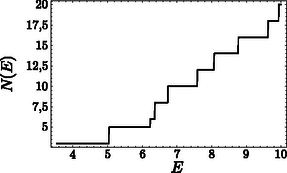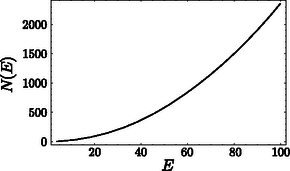$N\left(E\right)$ azon energiaszintek számát, amelyekre teljesül, hogy $E_n<E$. Ez a függvény ugrásszerűen változik, ún. lépcsőfüggvény, amint azt a kinagyított 1. ábra mutatja. Ha viszont $N\gg 1$ esetben az $N\left(E\right)$ függvény ábráját nagyítás nélkül vizsgáljuk, az összefüggés egy folytonos, sima függvénnyel közelíthető (2. ábra).     1. ábra     2. ábra   A lépcsőfüggvény (pontosabban $N\left(E\right)$ kisimított változatának) növekedési ütemét (deriváltját) kiszámítva a $\begin{array}{c}{\displaystyle \varrho \left(E\right)=\frac{dN\left(E\right)}{dE}}\end{array}$ (4) állapotsűrűség nevű mennyiséget kapjuk. Első ránézésre egy kicsit mesterkéltnek tűnik ez a fogalom, de a kísérletek kiértékelése szempontjából ez az egyik legfontosabb fizikai mennyiség. Például egy zárt rendszerhez elektromos kontaktusokat csatlakoztatva és azokon feszültség- és áramerősség-méréseket végezve az eredmények kiértékelése annak ismeretében végezhető el, hogy tudjuk: a rendszer vezetőképessége arányos a rendszer állapotsűrűségével. Ennek további részletezésére (például a lépcsőfüggvény alakja, szerkezete) itt nincs lehetőségünk, az érdeklődő Olvasó ezt megtalálhatja a hivatkozott diákköri dolgozatban. Záró megjegyzésként még két dologról kell szót ejtenünk. Az egyik valószínűleg az Olvasóban is felmerült: mi van akkor, ha nem középen van a membránon a lyuk? Ez az eset sokkal bonyolultabb a koncentrikus esetnél, de numerikusan ekkor is meghatározhatók a sajátfrekvenciák. Ez a rendszer azért különösen érdekes, mert a neki megfelelő biliárd a klasszikus fizika törvényei szerint kaotikus mozgáshoz vezet, míg a koncentrikus eset nem kaotikus mozgásokat eredményez. Miután a klasszikus fizikán belül jelentkező kaotikus jelenségeket az 1970-es években megértették, felmerült a kérdés, hogy ha egy rendszer klasszikusan kaotikus, akkor ez a tény hogyan nyilvánul meg (ha megnyilvánul egyáltalán) a rendszer kvantumos megfelelőjében. Ez vezetett el a kvantumkáosz témakörének kutatásához. Ha egy rendszer kaotikus, az a klasszikus mechanikában azt jelenti, hogy a közeli kezdőhelyzetekből (kezdőállapotokból) indított részecskék pályája az idő múltával egymástól exponenciálisan távolodik. Kvantummechanikában nincs értelme egy biliárdban pattogó részecske pályájáról beszélni, ott a kaotikus viselkedés másképp jelentkezik. Bebizonyították, hogy egy mikrorendszernél a kaotikus jelleg a rendszer energiszintjeinek spektrumából ismerhető fel. A dolgozatban beláttuk, hogy a koncentrikus elrendezés valóban nem kaotikus. A dolgozatban elért eredmények kisebb módosítással átvihetők egy másik rendszerre, az ún. mezoszkopikus gyűrűre. Mágneses térbe helyezve a gyűrűt, állandósult áramokat figyeltek meg benne. A rendszer mágneses szuszceptibilitását mérték, melyet elméleti úton is meghatároztak, de az elméleti érték két nagyságrenddel (!) kisebb a mért értéknél. Ezt a furcsaságot a 90-es évek elején kezdték el vizsgálni, és azóta sem találtak kielégítő elméleti magyarázatot rá. A szuszceptibilitás függ a rendszer állapotsűrűségétől. Sejtésünk alapján az állapotsűrűségben fellépő szingularitások (amikre itt nem tudtunk kitérni) magyarázatot adhatnak a meglepő kísérleti eredményekre. 1Az alább bemutatásra kerülő cikk annak a tudományos diákköri dolgozatnak rövid kivonata, amelyet a szerző az ELTE TTK Komplex Rendszerek Fizikája Tanszékén készített, témavezetője Cserti József volt. Hagymási Imre, az ELTE III. éves fizikus hallgatója a 2007. évi XXVIII. Országos Tudományos Diákköri Konferencián I. díjat nyert.