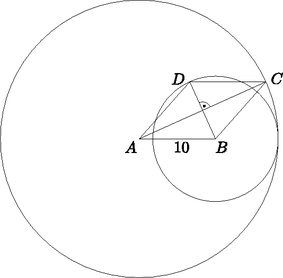Cím:	Megoldásvázlatok a 2006/4.sz emelt szintű gyakorló feladataihoz
Szerző(k):	Csík Zoltán
Füzet:	2006/május, 282 - 286. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Két konvex sokszög belső szögösszegének különbsége megegyezik egy hétszög belső szögösszegével, és egyiküknek kétszer annyi csúcsa van, mint ahány oldala a másiknak. Hány átlójuk van összesen?   Megoldás. A két sokszög csúcsainak száma legyen $n$ és $m$. Ekkor a belső szögeik összege $\left(n-2\right)\cdot {180}^{\circ }$, illetve $\left(m-2\right)\cdot {180}^{\circ }$. Ezek különbsége egy hétszög belső szögösszegével egyezik meg, azaz $\left(n-m\right)\cdot {180}^{\circ }=\left(7-2\right)\cdot {180}^{\circ }$, ahonnan az $n-m=5$ összefüggést kapjuk. Tudjuk, hogy az egyiknek kétszer annyi csúcsa van, mint ahány oldala a másiknak, de egy sokszögnek ugyanannyi csúcsa van, mint oldala, ezért $2m=n$. Az egyenletrendszerből kapjuk: $n=10$ és $m=5$. Az átlók száma: $\frac{n\left(n-3\right)}{2}=\frac{10\left(10-3\right)}{2}=35$, illetve $\frac{m\left(m-3\right)}{2}=\frac{5\left(5-3\right)}{2}=5$. Vagyis összesen 40 átlójuk van.   2. Oldjuk meg a következő egyenletrendszert a pozitív egész számpárok halmazán: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^{y^2-15y+56}}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle y-x}& {\displaystyle =5.}\hfill \end{array}}$   Megoldás. Az első egyenlet teljesüléséhez vagy az $y^2-15y+56$-nak kell 0-nak lennie, amiből az $y^2-15y+56=\left(y-7\right)\left(y-8\right)$ miatt $y=8$ vagy $y=7$; vagy az $x$-nek kell 1-nek lennie. A második egyenlettel összevetve az eredményeket három számpár elégíti ki az egyenletrendszert: $\left(3;8\right)$, $\left(2;7\right)$, $\left(1;6\right)$.   3. A $k^2\left(2+4x\right)-x\left(x+1+k\right)+3\left(x-2\right)\left(2k+1\right)-\left(1-x\right)\left(k+3\right)=0$ egyenlet gyökei $x_1=1$ és $x_2=2$. Adjuk meg $k$ értékét.   Megoldás. Ha $x_1=1$, akkor ezt az egyenletbe helyettesítve 0-t kell kapnunk: $\begin{array}{c}{\displaystyle k^2\left(2+4\right)-\left(1+1+k\right)+3\left(1-2\right)\left(2k+1\right)-\left(1-1\right)\left(k+3\right)=\mathrm{0,}}\end{array}$ rendezve: $6k^2-7k-5=0$, ennek megoldásai: $k_1=\frac{5}{3}$, $k_2=-\frac{1}{2}$. Hasonlóan, ha $x_2=2$, akkor $\begin{array}{c}{\displaystyle k^2\left(2+8\right)-2\left(2+1+k\right)+3\left(2-2\right)\left(2k+1\right)-\left(1-2\right)\left(k+3\right)=\mathrm{0,}}\end{array}$ rendezve: $10k^2-k-3=0$, ennek megoldásai: $k_1=\frac{3}{5}$, $k_2=-\frac{1}{2}$. Mivel mind a két feltételnek teljesülnie kell, azért $k=-\frac{1}{2}$.   4. Egy teázóban úgy szolgálják fel a teát, hogy a csésze 16 db kockacukorral az ábrán látható módon körberakható (a szomszédos kockacukrok csúcsai összeérnek, egy-egy oldalukkal érintik a csészét, két-két csúcsuk pedig a csészealj peremén van). Hány cm a kockacukor éle, illetve a csésze sugara, ha a csészealj átmérője 10 cm?       Megoldás. Egy kockacukorhoz $\frac{2\pi }{16}$ nagyságú középponti szög tartozik. Ezt megfelezve és az $OC$ sugarat berajzolva az $AOE$ derékszögű háromszögben $r=\frac{x}{2}\cdot \text{ctg}\left(\frac{\pi }{16}\right)$, az $OCF$ derékszögű háromszögben pedig  $R^2={\left(x+r\right)}^2+{\left(\frac{x}{2}\right)}^2$.     Ebben az egyenletben $R=5$ és $\text{ctg}\left(\frac{\pi }{16}\right)\approx 5$ alapján $r\approx \frac{5}{2}x$. A következő ,,egyenletet'' kapjuk: $\begin{array}{c}{\displaystyle 25\approx {\left(x+\frac{5}{2}x\right)}^2+{\left(\frac{x}{2}\right)}^2\mathrm{,}}\end{array}$ ahonnan $x\approx \sqrt[]{2}$, azaz a kockacukor éle kb. 1,4 cm, a csésze átmérője kb. 7 cm.   II. rész   5. Hány megoldása van az $|||||x|-1|-1|-1|-1|=\frac{kx}{7}$ egyenletnek a pozitív egész $k$ értékétől függően?   Megoldás. Készítsünk vázlatrajzot az $f\left(x\right)=|||||x|-1|-1|-1|-1|$ függvényről:     Az $f\left(x\right)$ függvénynek az 1 meredekségű egyenessel végtelen sok közös pontja, az $\frac{1}{3}$ meredekségű egyenessel 4 közös pontja van, és ezek a ,,választóvonalak''. Ha $k>7$, akkor egy, ha $k=7$, akkor végtelen sok, ha $k\in \left\{6;5;4;3\right\}$, akkor három, és ha $k\in \left\{2;1\right\}$, akkor öt megoldása van az egyenletnek.   6. Adott a $10$ egység oldalú $ABCD$ rombusz. Az $A$ középpontú, $C$ csúcson áthaladó kört belülről érinti a $B$ középpontú, $D$ csúcson áthaladó kör. Határozzuk meg a rombusz területét.   Megoldás. Legyen a nagyobbik kör sugara, ami egyben a hosszabbik átló a rombuszban $R$, és a kisebbik kör sugara, amely a rövidebbik átló, $r$. Mivel a rombusz átlói merőlegesen felezik egymást, a Pitagorasz-tétel alapján: $\begin{array}{c}{\displaystyle \frac{R^2}{4}+\frac{r^2}{4}=100.}\end{array}$ Mivel pedig a két kör érinti egymást: $R-r=10$. A két összefüggésből a $\begin{array}{c}{\displaystyle 2r^2+20r-300=0}\end{array}$ másodfokú egyenletet kapjuk, melynek pozitív gyöke $r=5\sqrt[]{7}-5$, amiből $R=5\sqrt[]{7}+5$.     A rombusz területe: $\begin{array}{c}{\displaystyle t=\frac{Rr}{2}=\frac{\left(5\sqrt[]{7}-5\right)\left(5\sqrt[]{7}+5\right)}{2}=75.}\end{array}$   7. Az $x^2+y^2=25$ egyenletű kör, az $y=\frac{1}{3}{x}^2+1$ egyenletű parabola és az abszcisszatengely egy síkidomot határoznak meg, amelyet megforgatunk az abszcisszatengely körül. Mekkora a keletkezett forgástest térfogata?     Megoldás. Határozzuk meg a parabola és a kör metszéspontjainak koordinátáit. A két egyenletből a metszéspontok: $A\left(-3;4\right)$ és $B\left(3;4\right)$. A keletkezett forgástest térfogata: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V}& {\displaystyle =2\pi \left[\underset{0}{\overset{3}{\int }}{\left(\frac{1}{3}{x}^2+1\right)}^{2}dx+\underset{3}{\overset{5}{\int }}\left(25-x^2\right)dx\right]=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\pi \left[\underset{0}{\overset{3}{\int }}\left(\frac{x^4}{9}+\frac{2x^2}{3}+1\right)dx+\underset{3}{\overset{5}{\int }}\left(25-x^2\right)dx\right]=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\pi {\left[\frac{x^5}{45}+\frac{2x^3}{9}+x\right]}_0^3+2\pi {\left[25x-\frac{x^3}{3}\right]}_3^5=\frac{144}{5}\pi +\frac{104}{3}\pi =\frac{952}{15}\pi \approx 199\mathrm{,}4.}\hfill \end{array}}$   8. Egy cég golyó alakú, tömör rágógumit gyártott, és darabját $10$ forintért adta el. Az alapanyagok drágulása miatt az előállítási költség $300\%$-kal növekedett. A gyártó szeretné, ha a rágógumik eladása utáni nyereség és az előállítási költség aránya nem változna, ezért a rágógumi darabárát $20$ forintra emelte. A terméket is átalakították: a 2 cm átmérőjű gömb alakú rágógumik belseje egy koncentrikus gömb alakú üreget is tartalmaz. Számoljuk ki az új rágógumi falának vastagságát.   Megoldás. Legyen a régi fajta rágógumi előállítási költsége $x$ Ft, és legyen az új és a régi rágógumi mennyiségének (tömegének) aránya $y$ $\left(x\mathrm{,}y\ne 0\right)$. Ekkor a következő táblázatot készíthetjük: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|ccc|}\hline \multicolumn{1}{c}{{\displaystyle }}& {\displaystyle \text{Régi fajta}}\hfill & \hfill {\displaystyle \text{Új fajta }}\hfill \\ {\displaystyle \text{Az előállítás költsége (Ft)}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn><mi>x</mi><mi>y</mi></math>}}\hfill \\ {\displaystyle \text{Az eladási ár (Ft)}}\hfill & \hfill {\displaystyle \text{10}}\hfill & \hfill {\displaystyle \text{20}}\hfill \\ {\displaystyle \text{Nyereség darabonként (Ft)}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>10</mn><mo stretchy="false">-</mo><mi>x</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>20</mn><mo stretchy="false">-</mo><mn>4</mn><mi>x</mi><mi>y</mi></math>}}\hfill \\ {\displaystyle \text{Arány}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>10</mn><mo stretchy="false">-</mo><mi>x</mi></mrow><mrow><mi>x</mi></mrow></mfrac></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="14pt" width="0pt" depth="8pt"></mspace></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>20</mn><mo stretchy="false">-</mo><mn>4</mn><mi>x</mi><mi>y</mi></mrow><mrow><mn>4</mn><mi>x</mi><mi>y</mi></mrow></mfrac></mrow></math>}}\hfill \\ \hline\end{array}}}\end{array}$ Mivel az előállítás után a nyereség/költség arány nem változott, azért: $\begin{array}{c}{\displaystyle \frac{10-x}{x}=\frac{20-4xy}{4xy}\mathrm{,}\text{ahonnan}y=\frac{1}{2}\mathrm{.}}\end{array}$ Az új rágógumi anyagfelhasználása fele a régiének, a belsejében lévő üres gömb sugara $\sqrt[3]{\frac{1}{2}}$. Így a rágógumi falának vastagsága $1-\sqrt[3]{\frac{1}{2}}\approx 0\mathrm{,}2$ cm.   9. Oldjuk meg az alábbi egyenletrendszereket: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{x-4}+\sqrt[]{x-5}-1}& {\displaystyle =7x-x^2-2xy\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{log}{}_5{64}^x\cdot \text{log}{}_4{125}^y}& {\displaystyle =45.}\hfill \end{array}}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle }& {\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle xy+y}& {\displaystyle =\mathrm{2,}}\hfill \\ \hfill {\displaystyle \left(1-y\right)\cdot 2\text{cos}\frac{x\cdot \pi }{3}}& {\displaystyle =\frac{x-1}{x+1}\mathrm{.}}\hfill \end{array}}}\hfill & \text{(<mi>*</mi>)}\end{array}}$   Megoldás. $a)$ A feladatban $x\ge 5$-nek teljesülni kell. A második egyenlet bal oldalát átalakítva: $\begin{array}{c}{\displaystyle \text{log}{}_5{64}^x\cdot \text{log}{}_4{125}^y=\text{log}{}_5{4}^{3x}\cdot \text{log}{}_4{5}^{3y}=3x\cdot \text{log}{}_{5}4\cdot 3y\cdot \text{log}{}_{4}5=9xy\cdot \underset{1}{\overset{}{\underbrace{\text{log}{}_{5}4\cdot \text{log}{}_{4}5}}}=9xy\mathrm{,}}\end{array}$ ahonnan $xy=5$. Az első egyenletbe behelyettesítve: $\begin{array}{c}{\displaystyle \sqrt[]{x-4}+\sqrt[]{x-5}-1=7x-x^2-10=\left(x-5\right)\left(2-x\right)\mathrm{.}}\end{array}$ A kikötések miatt $x\ge 5$. A bal oldal szigorúan monoton nő, nem negatív és csak $x=5$-nél egyenlő 0-val. A jobb oldal $x\ge 5$ esetén nem pozitív, és $x=5$ esetén 0. Így csak az $x=5$ megoldás. Az egyenletrendszer megoldása: $\left(5;1\right)$. $b)$ Az $x=-1$ jól láthatóan nem megoldás. Ha $x\ne -1$, akkor az első egyenletből: $y=\frac{2}{x+1}$. A második egyenletbe beírva: $\begin{array}{c}{\displaystyle \left(1-\frac{2}{x+1}\right)\cdot 2\text{cos}\frac{x\cdot \pi }{3}=\frac{x-1}{x+1}\mathrm{.}}\end{array}$ A bal oldalt tovább alakítva: $\begin{array}{c}{\displaystyle \left(\frac{x+1}{x+1}-\frac{2}{x+1}\right)\cdot 2\text{cos}\frac{x\cdot \pi }{3}=2\cdot \frac{x-1}{x+1}\cdot \text{cos}\frac{x\cdot \pi }{3}\mathrm{.}}\end{array}$ A $2\cdot \frac{x-1}{x+1}\cdot \text{cos}\frac{x\cdot \pi }{3}-\frac{x-1}{x+1}=0$ egyenletet kell megoldanunk. Szorzattá alakítva: $\frac{x-1}{x+1}\left(2\text{cos}\frac{x\cdot \pi }{3}-1\right)=0$. Innen kapjuk, hogy $x=1$, illetve $\text{cos}\frac{x\cdot \pi }{3}=\frac{1}{2}$. Mivel $\begin{array}{c}{\displaystyle \frac{1}{2}=\text{cos}\left(\frac{\pi }{3}+2k\pi \right)=\text{cos}\pi \left(\frac{1+6k}{3}\right)\mathrm{,}\text{illetve}\frac{1}{2}=\text{cos}\left(\frac{5\pi }{3}+2l\pi \right)=\text{cos}\pi \left(\frac{5+6l}{3}\right)\mathrm{,}}\end{array}$ ezért a két megoldáscsoport $x=6k+1$, illetve $x=6l+5$, ahol $k\mathrm{,}l\in Z$, és ebben az $x=1$ is benne van. A megoldások: $\left(6k+1;\frac{1}{3k+1}\right)$, ahol $k\in \text{Z}$, illetve $\left(6l+5;\frac{1}{3l+3}\right)$, ahol $l\in \text{Z}$.