| Cím: | Beszélgetés az Abel-díjas Lax Péterrel | ||
| Szerző(k): | Ratkó Éva | ||
| Füzet: | 2006/május, 277 - 282. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Lax Péter 1926. május 1-jén született Budapesten. Szüleivel és bátyjával 1941-ben kimenekült Amerikába, és azóta ott él. A világ egyik legelismertebb matematikusa, számos díj, elismerés birtokosa. Annak ellenére, hogy New Yorkban igen kevés lehetősége van magyarul beszélni, itthon sokszor tart magyar nyelven előadást. Kedvenc regénye Jókai Az élet komédiásai című műve, melyet feleségének (Jókai több más regényével együtt) le is fordított angolra. ─ Neked hogy tetszett a ,,Petrosz bácsi''-könyv?1 Milyen volt a visszhangja? ‐ Nem tudom, hogy milyen volt a visszhangja, én kicsit gyerekesnek találtam. És van benne egy matematikai hiba. Úgy emlékszem, az a könyv poénja, hogy a Goldbach-tétel nem eldönthető. Itt van: ,,Jusson eszedbe Kurt Gödel, Petrosz bácsi. Jusson eszedbe a nemteljességi tétel Goldbach sejtése2 bizonyíthatatlan!'' Na mármost, ha bizonyíthatatlan, akkor igaz. Mert ha eldönthetetlen lenne, akkor abból következne, hogy nem létezik olyan páros szám, ami nem írható föl két prím összegére. Mert minden páros számra el lehet dönteni, hogy felírható-e két prímszám összegeként. Úgyhogy ha az ember találna egy olyan páros számot, ami nem írható fel, az megcáfolná Goldbach tételét. Ebből következik, hogy nem létezik ilyen páros szám, tehát Goldbach tétele igaz. Ez persze egy metamatematikai érvelés. De ha úgy mondjuk ki a Goldbach sejtést, hogy egy véges számú halmazt kivéve minden páros szám felírható két prímszám összegeként, akkor ez a sejtés lehet eldönthetetlen. Nem áll rá az előbbi érvelés. Bosszant, hogy ha hamis matematikai tételeket olvasok egy könyvben. ─ Nem matematikus ismerőseim azt mondták, megértették belőle, hogy a matematika művészet. Nem az, amit a középiskolai emlékek alapján gondoltak róla. ‐ Akkor jó. Ha egy nem matematikusnak ad egy képet arról, hogy milyen a matematika, akkor jó. ─ Az ankéton mondtad az előadás elején, hogy annak idején Te is feladatmegoldó voltál. ‐ Igen, én is oldottam a KöMaL-t. ─ Emlékszel a Trefortbeli idődből valami olyan matematikai feladatra, amelynek megragadott a megoldása? Vagy valamire, ami matematikával kapcsolatos? ‐ Van egy érdekes emlékem. A tanárunk az algebrát vezette be és azt mondta, hogy ha a rendőrség nyomoz valakit, akkor az első dolog, amit tesznek, hogy elnevezik XY-nak. Amerikában úgy hívják XY-t, hogy John Doe. Ha van elég információnk, akkor ki lehet következtetni, hogy ki az a John Doe. Az algebrában, ha felírjuk, hogy mit tudunk -ről, vagy ha két ismeretlen van, akkor -ről és -ról, akkor ha van elég információnk, meg tudjuk határozni -et és -t. Engem ez megragadott. A legtöbb kezdő fiatal matematikus először a geometriába szeret bele. Először én is a geometriába szerettem bele. De csak nagyon kevesen lesznek geométerek. Ez érdekes kérdés: miért van az, hogy a geometria először annyira vonzza az embert. Azt hiszem, azért, mert az a geometria, ami az iskolai gyerekeket megfogja, az mind síkgeometria, nagyon lapos. Az igazi, az izgató geometriában van görbülés. A síkgeometria nagyon egyenes, csak egyenesekből áll. Íme egy szép bizonyítás: a tétel az, hogy a háromszög belső szögeinek az összege 180 fok. Mennyi a külső szögeinek az összege? A külső és a belső szögeinek a nagysága összesen , így a külső szögeinek az összege . Tehát, ha a belső szögek összegét tudjuk, akkor kiszámíthatjuk a külső szögek összegét, és megfordítva, ha a külső szögek összege , abból következik, hogy a belső szögeké . Tehát elég azt bebizonyítani, hogy a külső szögek összege . Nomármost, hogy bizonyítjuk ezt be? (Egy tollat az egyik oldalhoz illeszt az ábra szerinti 1. helyzetbe, majd elforgatja a nyíl szerint a 2. helyzetbe, majd megint elforgatja a 3. helyzetbe, végül újra elforgatja, így a toll visszakerül az 1. helyzetbe.) Azonban először ennyi (mutatja) szöggel fordítottam el, aztán ennyi szöggel, végül ennyi szöggel, és a három szög összege . 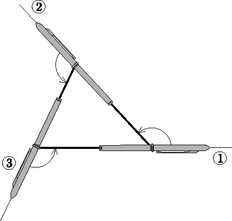 ─ És ezt ki találta ki? ‐ Nem tudom. Nagyon érdekes bizonyítás. Az, hogy a külső szögek összege , minden sokszögre fönnáll. Nem csak háromszögre, hanem ötszögre, hétszögre, tizenhétszögre és milliószögre. ─ Sokáig tartana elmutogatni. ‐ Nézzük az általánosítást. Vegyünk egy olyan poliédert, amelyből, ha felfújjuk, gömb lesz. Rajzoljunk egy sokszöget a lapjaira (lásd az ábrát). Mennyi a belső szögeinek az összege? És a külső szögeinek? Hogy definiálom itt a szögeket? A következő módon: minden egyes szöget az őt meghatározó két él síkjában mérek meg. Ha a sokszög síkban feküdne, akkor 360 fok lenne a külső szögeinek az összege. De nem síkban van, úgyhogy nem tudjuk, hogy mennyi az összeg. A válasz a görbüléssel van kapcsolatban. 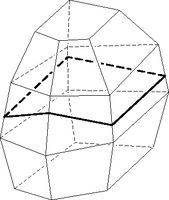 ─ Azt mondtad, hogy Te bárkinek el tudod magyarázni a matematikát. ‐ Azt mondtam? ─ Ha érdekli. ‐ Ha érdekli. ─ Ebben a cikkben3 nem értettem ezt a részt: a valós folyamatok időbeli megfordíthatatlanságáról van szó, az entrópiáról. ‐ Azt tudod, hogy az entrópia növekszik? ─ Azt sem tudom, mi az az entrópia. ‐Az entrópiát nem lehet olyan könnyen megmagyarázni. Ha van két tálunk, az egyikben forró, a másikban hideg víz, akkor ha összeöntjük őket, langyos vizet kapunk. De nincs olyan fizikai eljárás, amelynek a segítségével egy tál langyos vizet szét lehetne választani forró vízre és hideg vízre. A hideg és a forró víz összekeverése visszafordíthatatlan. Ez egy nagyon fontos fizikai tény, a hidrodinamikának nagyon fontos alapelve. Igazából a termodinamikának az alapelve, de legfontosabb alkalmazása a hidrodinamikában van. ─ És ez kapcsolatban van a differenciálegyenletekkel? ‐ Igen. Meglepő és mulatságos, hogy hogyan kerül ez ki a differenciálegyenletekből. Ezen magam is csodálkoztam. Ez egy tanulságos dolog, de ahhoz túl sok matematika kell, hogy elmagyarázzam. ─ Elég sok mindennel foglalkoztál. Van olyan probléma, amelynek a leginkább megörültél? ‐ A lökéshullámok kiszámítása, az volt nagyon mulatságos. Sok minden mulattatott, és van öt-hat dolog, amire nagyon szívesen emlékszem vissza. ─ Nálatok milyen az egyetemi oktatás? Nálunk vannak előadások és gyakorlatok, ahol feladatokat oldanak meg. ‐ Az alapvető kurzusokon, mint például az integrál- és differenciálszámítás, vannak gyakorlatok. Gyakran fordul elő, hogy egy alapvető integrál- és differenciálegyenleti kurzuson van 100 hallgató vagy még több. Én nem szeretek annyi embert tanítani, mert nem is lehet. Egészen másképpen kell tanítani, és vannak, akik tudnak hatékonyan tanítani ilyen tömeget. Én nem nagyon, inkább 30-at tanítok szívesen. Ha százan vannak, akkor elvesztem a kapcsolatot a hallgatókkal. Akkor olyan a hallgató, mint aki a tv-t vagy a mozivásznat nézi ‐ nézi vagy nem nézi, inkább nem nézi. ─ Az Ankéton is sokan voltak az előadásodon. ‐ Jó sokan voltak, de ott nagyon jól éreztem magam, mert tudtam, hogy mindenkit érdekel. Az egyetemen pedig nagyon sokan felveszik, mert kötelező tárgy. Biológusoknak is kell például egy szemeszter matematika, meg a fizikusok is felveszik, őket inkább érdekli, de azt is mondják, hogy a matematikusok sok mindent tanítanak, ami nem érdekli a fizikusokat. A fizikusokat az érdekli, hogy hogyan lehet a matematikai fizika differenciálegyenleteit megoldani, a többi ,,quatch''. ─ És középiskolásoknak tanítottál valaha valamit? ‐ Egyszer előadtam. New Yorkban van pár nagyon jó gimnázium. Az egyik a Stuyvesant High School. Amikor Amerikába jöttem '41 végén, akkor '42 februárjában felvettek a Stuyvesant High Schoolba, és egy évre rá be is fejeztem. Csak 6.-ban jöttem, de a magyar iskolákban többet tanítottak, úgyhogy egy év múlva, amikor pedig csak a 7. osztály felét fejeztem volna be, már eleget tudtam az érettségihez. És aztán 60 év után megkértek, hogy menjek vissza abba az iskolába és tartsak egy előadást azoknak, akik már elég magas matematikai kurzusra járnak. Úgyhogy nem tömegnek, csak 30-40 diáknak adtam elő. A mulatságos az volt, hogy a legidősebb unokám, Tommy ugyanabba a gimnáziumba járt. De nagy változások voltak. Az én időmben a Stuyvesant High Schoolba csak fiúkat vettek fel. Aztán ez megváltozott a háború után. Van egy kedves barátom, aki ügyvéd és a szabadsági ügyek kifejezetten érdeklik. Ha valakit jogfosztás ér, akkor ő síkra száll. A leghíresebb eset az volt, amikor a feketéket külön iskolába járatták délen, miután a rabszolgaság megszűnt. Volt egy híres törvényszéki ítélet: lehet két különböző iskola feketéknek és fehéreknek, de egyenlő nívón kell lenniük. Persze ez hazugság volt, sosem volt egyenlő a nívó, a fehér iskolákban a tankönyvtől kezdve minden jobb, illetve több volt. Az '50-es években aztán megint volt egy nagy per, amiben azt bizonyították, hogy nem lehet egyenlő a nívó, mert ha különválasztják a feketéket, akkor már maga ez a tény nagyon káros hatással van rájuk. És megvolt a törvényszéki ítélet ‐ egyértelműleg egyetértett. Ez egy nagyon fontos és híres bírói döntés volt. Szóval ez a kedves barátom, aki ügyvéd és ilyen ügyek érdeklik, pert indított New York városa ellen, hogy ez a kiváló iskola, a Stuyvesant High School, ami különösen matematikára és tudományra tanítja a diákokat, de csak fiúkat vesznek fel és lányokat nem, nem adja meg ugyanazt az esélyt a lányoknak, mint a fiúknak. És már előre látta: híres per lesz, aminek ő a hőse. De New York városa rögtön beleegyezett. Ez az egyik változás a Stuyvesant High Schoolban. A másik az, hogy a régi iskolai épület helyett, ahova én jártam (egy nagyon régi, három emeletes, nem nagyon jó, kicsit lábszagú hely volt) egy magas, hét emeletes, rém előkelő épület van, mindenféle laboratóriummal, auditóriummal, szép nagy sporttermekkel. Oda járt az unokám. Ez a szép, új iskola csak négy blokknyira volt a World Trade Centertől, amibe ‐ emlékszel ‐ szeptember 11-én beleröpültek. Úgyhogy az unokám ott volt négy blokknyira az egésztől. Hála Istennek, semmi sérülés nem volt az iskolában. Persze gyalog kellett hazamenniük, és egy kicsit aggódtam. ─ Látták? ‐ Mindent láttak. Látta, hogy az emberek kiugranak az ablakon. Látta, hogy összeomlik. De erős idegei vannak, úgyhogy nem roppantotta meg. Ilyesmi is előfordul az életben. ─ És miről beszéltél nekik? ‐ A következő érdekes problémáról. Tudjátok, mik a prímszámok, ugye? Még egy muzsikus is tudja. Azt is tudjátok, hogy minden más számot, ún. összetett számot faktorizálni lehet prímszámokra. Az aritmetika egyik alapvető tétele az, hogy csak egyféleképpen lehet prímszámokra faktorizálni. Amikor az ember először hallja ezt és utánagondol, akkor azt mondja: teljesen világos. Ha még egy kicsit meggondolja, már nem olyan teljesen világos. S ha még egyszer meggondolja, akkor: ,,miért van ez?''. Szóval ez egy nagyon nem, egyáltalában nem könnyen bizonyítható tény. Ezt bizonyítottam be. Egy óráig tartott. ─ És sikerült? ‐ Előre kellett készülni. Még egy hivatásos matematikusnak is kicsit utána kell gondolnia, hogy hogy is van ez a bizonyítás. Aztán ennek általánosításáról is beszéltem. Szóval erről adtam elő. Ha legközelebb előadok, azt hiszem, arról fogok mesélni, amiről a KöMaL-os gyerekeknek is, a kockákkal és a háromszöggel. ─ A Pólya-függvényt4 nem ismerték, többen mondták, hogy nagyon tetszett nekik, nem is hallottak róla eddig. ‐ Nem is hallották? Ez jó, ennek örülök. 1914-ben jelent meg. ─ Úgy tudom, hogy mindennap bemész az egyetemre. Mivel töltöd ott az időt? ‐ Rendszerint délre megyek be és hatra érek haza. Megnézem az e-mailemet, beszélek a barátaimmal, néha használom a könyvtárat. Mindig van valami. Sosem unatkozom. ─ Dolgozol is vagy azt inkább otthon? ‐ Dolgozom is. Reggel otthon dolgozom. ─ És tanítasz is? ‐ Nem tanítok, már hat éve nyugdíjba mentem. Amerikában van egy törvény, hogy a kora miatt senkit sem lehet nyugdíjba vonulásra kényszeríteni. Ez mindenkire vonatkozik, a professzorokra is, meg a földmunkásokra (kapálókra, kaszálókra) is. Én mindig úgy gondoltam, hogy egy olyan törvény, ami egy gödröt ásó munkásra és egy professzorra is alkalmazható, az nem lehet nagyon jó törvény. A régi szabály az volt, hogy 70 évesen nyugdíjba kell menni. Mikor 70 éves lettem, még két évig maradtam félidőre, és aztán teljesen visszavonultam. Szerintem ez a helyes. Néha van egy-két professzor, aki nem hajlandó. ─ Itthon is van ilyen. ‐ Itthon nincs ilyen törvény? Mesélek egy mulatságos történetet egy barátomról. A Berkeley-i egyetemen matematikus és már közeledik a 80-hoz. Nem volt hajlandó visszavonulni. A hallgatói már azt kívánták, hogy menjen a pokolba. De nem lehetett a kora miatt nyugdíjba vonulásra kényszeríteni. Más okból persze lehetett. Így a tanszék megkérte az adminisztrációt, hogy tegyék a visszavonultak listájára, abból az okból, hogy gyatrák az előadásai. Az egyetem szabályai szerint az illetékes védheti magát, és ő védte is magát. A védelem az volt, hogy ,,az előadásaim mindig gyatrák voltak''. ─ És mi lett a vége? ‐ Azt hiszem, végleg visszavonult. ─ Vannak kollégák, akikkel tudsz magyarul beszélni? ‐ Van egy kollégám Michiganban, együtt dolgozunk és néha összejövünk vagy telefonon beszélünk. Máskülönben nincs sok alkalmam magyarul beszélni. 1Aposztolosz Doxiadisz: Petrosz bácsi és a Goldbach sejtés, Európa Kiadó (Budapest, 2004).2Goldbach sejtése szerint minden 2-nél nagyobb páros szám fölírható két prím összegeként.3Fritz József: Lax Péter tudományos munkásságáról (Természet Világa, 2005. június, http://www.kfki.hu/cheminfo/TermVil/szamok/tv2005/tv0506/lax5.html)4A Pólya-féle függvény definíciója a következő: Legyen és legyen adva egy nem egyenlő szárú derékszögű háromszög. Írjuk fel -t kettes számrendszerben: Állítsunk merőlegest a derékszögű csúcsból az átfogóra. Így két hasonló háromszögre bontottuk az eredeti háromszöget. Ha , akkor válasszuk ki a nagyobbikat, ha pedig , akkor a kisebbiket. Ezután a választott háromszög derékszögű csúcsából állítsunk merőlegest az átfogójára, majd értékétől függően válasszunk a keletkezett két kisebb háromszögből. Ezt az eljárást folytatva, a határérték egy pont, ez lesz . Bizonyítható, hogy a háromszög minden pontja előáll, valamint az is, hogy folytonos. |