Kezdőlap


Cím:	A transzformátor mechanikai hasonmása
Szerző(k):	Halász Gábor
Füzet:	2006/április, 233 - 238. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismert tény, hogy számos elektromos áramkörnek létezik mechanikai hasonmása (analogonja), vagyis egy olyan mechanikai rendszer, melynek viselkedését, mozgását formailag az áramkörével megegyező egyenletek írják le. A két egyenletrendszerben a fizikai mennyiségek páronként megfeleltethetőek egymásnak, és emiatt természetesen az egyenletek (megfelelő kezdőfeltételekhez tartozó) megoldása is azonos alakú. A két rendszer (a mechanikai és az elektromos) valamilyen szinten hasonlóan is viselkedik, bizonyos jelenségek az egyik rendszerben összekapcsolhatók a másik rendszer látszólag egészen eltérő jelenségeivel.
Mire is lehet használni egy ilyen analógiát? Általában igaz, hogy egy bonyolult, váltóáramra kapcsolt, kondenzátorokkal és tekercsekkel telepakolt áramkör működését nehezebb első látásra megérteni, ,,átérezni'', mint egy egyszerű mechanikai rendszerét. Az analógia segítségével esetleg könnyebben felismerhetünk fontos dolgokat az áramkör viselkedésével kapcsolatban, méghozzá az esetenként igen bonyolult egyenletek megoldása nélkül.
A klasszikus példa az elektromos-mechanikai hasonlóságra a váltóáramú soros $R L C$ -kör, amely egy csillapított kényszerrezgéssel állítható analógiába. Ha ugyanis egy $k$ erősségű rugó egyik végére egy $m$ tömegű testet erősítünk, a másik végét pedig egy adott $y (t)$ függvénynek megfelelő módon mozgatjuk, továbbá a testre a sebességével arányos közegellenállási erő is hat, akkor a test $x (t)$ elmozdulására vonatkozó Newton-egyenlet:

\begin{matrix} m \ddot{x} (t) = k [y (t) - x (t)] - λ \dot{x} (t), \end{matrix}

azaz

\begin{matrix} m \ddot{x} (t) + λ \dot{x} (t) + k x (t) = k y (t), \end{matrix}

(1)

ahol az

x

feletti ,,pont'' az idő szerinti változási sebességet (deriváltat), a két pont pedig a gyorsulást (második deriváltat) jelöli. Mivel egy soros

R L C

-körben a

Q (t)

töltéssel rendelkező

C

kapacitású kondenzátoron a feszültség

\frac{Q (t)}{C}

, az áramerősség

\dot{Q} (t)

, így az

R

ellenálláson

R \dot{Q} (t)

és az

L

induktivitású tekercsen

L \dot{I} (t) = L \ddot{Q} (t)

feszültség esik, az

U (t)

feszültségre kapcsolt soros kör egyenlete:

\begin{matrix} L \ddot{Q} (t) + R \dot{Q} (t) + \frac{1}{C} Q (t) = U (t) . \end{matrix}

(2)

Az (1) és (2) egyenletet összevetve látható a hasonlóság, és az is leolvasható, hogy a különböző elektromos mennyiségeknek milyen mechanikai mennyiség a párja. (Az

U (t)

váltófeszültség a mozgást gerjesztő

y (t)

elmozdulás

k

-szorosának, a kondenzátor

Q (t)

töltése az

x (t)

elmozdulásnak, az

R

ellenállás a

λ

csillapítási együtthatónak, az

L

induktivitás a test

m

tömegének, a kapacitás reciproka pedig a

k

rugóállandónak felel meg.)
A mozgást (illetve az áramkört) leíró egyenletet nem könnyű megoldani, a mechanikai analógiát (vagyis a kényszerrezgést) végiggondolva néhány dolgot meg lehet ,,érezni'' az elektromos rendszerrel kapcsolatban. Ha például a gerjesztés periodikus és a frekvenciája elég kicsi, akkor a test a rugó másik végével együtt mozog, a rugó nyújtatlan marad. Ilyenkor tehát a test periodikus elmozdulása a gerjesztéssel azonos fázisú, és az amplitúdója is arányos (nevezetesen megegyezik) a gerjesztés amplitúdójával. Ha viszont a gerjesztési frekvencia nagyon nagy, a test nem tudja követni a rugó másik végének nagyon gyorsan váltakozó mozgását, az amplitúdó gyakorlatilag nullára csökken. Ekkor a közegellenállási erő elhanyagolható a rugóerő mellett, és emiatt az

x (t)

elmozdulás

y (t)

-vel ellentétes fázisú rezgéssel írható le. A rendszer sajátfrekvenciájának közelében fellép a rezonancia jelensége: az

x (t)

elmozdulás a gerjesztéshez képest

90^{\circ}

-os fázistolásba, a sebesség viszont a gerjesztéssel azonos fázisba kerül. A külső erő ilyenkor folyamatosan pozitív munkát végez a rendszeren, így az amplitúdó növekedésének csak a csillapítás szab határt.
Használjuk az analógiát, és próbáljuk ezeket a megállapításokat az

R L C

-körre alkalmazni. Ha a váltóáram frekvenciája nagyon kicsi, a kondenzátor töltése minden pillanatban arányos a feszültséggel, éppen úgy, mintha az ellenállás és az induktivitás nem is lenne az áramkörben. Ha a frekvencia elég nagy, a kondenzátorra alig esik feszültség, és az is ellentétes fázisú a gerjesztő feszültséggel. Ekkor nyilván a tekercsre esik a feszültség legnagyobb része. Az analógia alapján megjósolhatjuk a feszültség-rezonancia jelenségét is, amely akkor lép fel, ha a gerjesztő frekvencia megközelít valamilyen, csak az

R L C

-körre jellemző frekvenciát (a sajátfrekvenciát). Mindezt anélkül állapíthatjuk meg, hogy az egyenleteket megoldanánk, vagy megpróbálnánk részletesen végiggondolni, mi is történik valójában egy

R L C

-körben.
A 2005. évi Eötvös-verseny 3. feladatával¹ kapcsolatban valószínűleg hozzám hasonlóan sokan mások is belebonyolódtak az egyenletekbe, annak ellenére, hogy a feladat megoldása tulajdonképpen igen egyszerű volt. A ,,jó minőségű transzformátor'' kifejezés nyilván a rendszert jellemző fizikai mennyiségeknek valamilyen határesetét jelenti, és az előző példából látszik, hogy éppen az ilyen határesetek érthetők meg könnyen egy alkalmas mechanikai analógia alapján. A verseny után kezdtem el mechanikai analógiát keresni a transzformátorra, amely segítségével annak viselkedése kvalitatív szinten megérthető, és esetleg még a számszerű kiértékelést is egyszerűbbé teszi.
Az 1. ábrán egy olyan transzformátor kapcsolása látható, amelynek a szokásostól eltérő módon nem csak a szekunder-, hanem a primer körét is ellenállással terheljük. A primer körbe iktatott tápegység feszültsége az idő ismert függvénye, például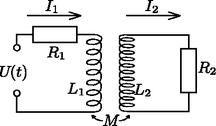

\begin{matrix} U (t) = U_{0} sin (ω t), \end{matrix}

de ettől eltérő módon is változhat. A tekercsek menetszámai

N_{1}

és

N_{2}

, ezek hányadosa legyen

N

, tehát

N_{2} = N \cdot N_{1}

. A kölcsönös indukciós együtthatót jelöljük

M

-mel, az önindukciós együtthatókat

L_{1}

-gyel és

L_{2}

-vel. Ha az első tekercs teljes fluxusa átmenne a másodikon, és viszont, igaz lenne, hogy

L_{1} = \frac{M}{N}

és

L_{2} = M N

. Mivel az induktív kapcsolat a tekercsek között nem lehet tökéletes, az önindukciós együtthatók valamivel nagyobbak ezeknél az értékeknél,

\begin{matrix} L_{1} = \frac{M}{N} + M_{1} és L_{2} = M N + M_{2} . \end{matrix}

Az ideális határesetben az induktív kapcsolat tökéletessé (ún. szoros csatolásúvá) válik, ekkor

\begin{matrix} M_{1} = M_{2} = 0. \end{matrix}

1. ábra

Írjuk fel a fenti jelöléseket alkalmazva Kirchhoff huroktörvényét a transzformátor primer körére:

\begin{matrix} U (t) = I_{1} R_{1} + L_{1} \dot{I_{1}} + M \dot{I_{2}}, \end{matrix}

vagyis

\begin{matrix} U (t) = R_{1} I_{1} + M_{1} \dot{I_{1}} + M (\frac{\dot{I_{1}}}{N} + \dot{I_{2}}) . \end{matrix}

(3a)

(Az áramerősségek jele feletti pont ‐ a mechanikai rendszernél alkalmazott írásmódhoz hasonlóan ‐ az időbeli változás sebességét, az időderiváltat jelöli.) A szekunder körre is felírhatjuk a megfelelő hurokegyenletet:

\begin{matrix} 0 = I_{2} R_{2} + L_{2} \dot{I_{2}} + M \dot{I_{1}}, \end{matrix}

tehát

\begin{matrix} 0 = R_{2} I_{2} + M_{2} \dot{I_{2}} + M (\dot{I_{1}} + \dot{I_{2}} N) . \end{matrix}

(3b)

Tekintsük most a 2. ábrán látható, három dugattyúval elzárt folyadéktartályt, melyben összenyomhatatlan, súrlódásmentes, elhanyagolható sűrűségű folyadék található. Megmutatjuk, hogy ez a ,,hidraulikus rendszer'' a szóban forgó transzformátor mechanikai hasonmásának tekinthető. Jelölje

m_{1}

m_{2}

és

m_{0}

a dugattyúk tömegét,

A_{1}

A_{2}

és

A_{0}

pedig a dugattyúk keresztmetszetét.

A_{2}

és

A_{1}

hányadosát

n

-nel jelöljük, vagyis

A_{2} = n A_{1}

. A folyadék nyomása (pontosabban a légköri nyomáshoz viszonyított többletnyomása) legyen

Δ p

, ez időben változó mennyiség is lehet.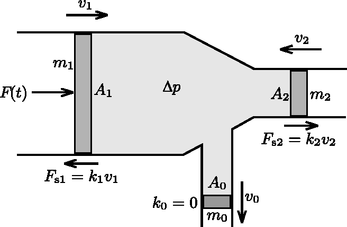

2. ábra

Tegyük fel, hogy a bal és a jobb oldali dugattyúkra a sebességükkel egyenesen arányos fékezőerő is hat, az arányossági tényezők

k_{1}

és

k_{2}

. (Ilyen fékezőerőt pl. egy erősen viszkózus folyadékban történő mozgásnál fellépő közegellenállás okozhat. A továbbiakban erre az erőre az egyszerűség kedvéért súrlódási erőként hivatkozunk.) Ha tehát a bal oldali dugattyú

v_{1}

sebességgel csúszik, a rá ható súrlódási erő

F_{s1} = k_{1} v_{1}

, és hasonló egyenlet igaz a jobb oldali dugattyúra is. Az alsó dugattyú viszont mozogjon súrlódásmentesen. (Az ,,alsó'' szóhasználat csak az ábrán való tájékozódást segíti, a három dugattyú mozgását vízszintes síkban képzeljük, így a gravitációs erőt nem kell számításba vennünk.)
A bal oldali dugattyúra időben adott módon változó

F (t)

erővel hatunk (ez lehet pl. periodikus, azaz

F_{0} sin (ω t)

alakú, de ettől eltérő módon is megadhatjuk), és szeretnénk meghatározni a dugattyúk mozgását. A rendszert négy ismeretlen mennyiség (

v_{1}

v_{2}

v_{0}

és

Δ p

) jellemzi, ezért négy egyenletre van szükségünk. Mindhárom dugattyúra felírhatjuk a Newton-féle mozgásegyenletet:

\begin{matrix} m_{1} {\dot{v}}_{1} & = F (t) - A_{1} Δ p - k_{1} v_{1}, \\ m_{2} {\dot{v}}_{2} & = - A_{2} Δ p - k_{2} v_{2}, \\ m_{0} {\dot{v}}_{0} & = A_{0} Δ p . \end{matrix}

A negyedik egyenletet az anyagmegmaradás törvénye szolgáltatja; összenyomhatatlan folyadéknál ez a térfogat megmaradásával egyenértékű:

A_{1} v_{1} + A_{2} v_{2} = A_{0} v_{0}

. Ezekből (

v_{0}

és

Δ p

kiküszöbölése után)

v_{1}

-re és

v_{2}

-re a következő két egyenletet kapjuk:

\begin{matrix} F (t) = k_{1} v_{1} + m_{1} {\dot{v}}_{1} + m_{0} \frac{A_{1} A_{2}}{A_{0}^{2}} (\frac{{\dot{v}}_{1}}{n} + {\dot{v}}_{2}), & (4a) \\ 0 = k_{2} v_{2} + m_{2} {\dot{v}}_{2} + m_{0} \frac{A_{1} A_{2}}{A_{0}^{2}} ({\dot{v}}_{1} + \frac{{\dot{v}}_{2}}{n}) . & (4b) \end{matrix}

Ha a (3a)‐(3b) egyenletrendszert (4a)‐(4b)-vel összehasonlítjuk, láthatjuk, hogy azok alakilag azonosak, feltéve, hogy az elektromos és a mechanikai mennyiségeket az alábbi módon feleltetjük meg egymásnak:

\begin{matrix} I_{1} & \Leftrightarrow v_{1}, & I_{2} & \Leftrightarrow v_{2}, \\ U (t) & \Leftrightarrow F (t), & N & \Leftrightarrow n, \\ R_{1} & \Leftrightarrow k_{1}, & R_{2} & \Leftrightarrow k_{2}, \\ M_{1} & \Leftrightarrow m_{1}, & M_{2} & \Leftrightarrow m_{2}, \\ M & \Leftrightarrow m_{0} \frac{A_{1} A_{2}}{A_{0}^{2}} . \end{matrix}

Az analógia felállítása után vizsgáljunk meg határeseteket, és próbáljuk a mechanikai modell alapján megjósolni, mi történik a transzformátorban. Az első speciális eset legyen az, amikor egy adott pillanatban

U_{0}

egyenfeszültséget kapcsolunk a primer körre. Ez a hidraulikus rendszer esetében azt jelenti, hogy a bal oldali dugattyúra állandó

F_{0}

erővel hatunk. Az erőhatás kezdetekor a belül hirtelen megnövekvő nyomás miatt a másik két dugattyú is megindul. Az alsó dugattyúra fékezőerő nem hat, így az a mozgása során csak gyorsulhat, a jobb oldali viszont a súrlódás miatt lassulhat is. Előbb-utóbb a bal oldali dugattyú akkora sebességre gyorsul fel, hogy a súrlódás már önmagában ellentart a külső nyomóerőnek, a nyomáskülönbség megszűnik. A jobb oldali dugattyú nyilván nem mozoghat tartósan nyomáskülönbség nélkül, a súrlódás előbb-utóbb megállítja. Ezért elég hosszú idő után, csak a bal oldali és az alsó dugattyú mozog állandó sebességgel, úgy, hogy az erőegyensúly és a térfogatmegmaradás is teljesüljön. A transzformátorra vonatkoztatva ez azt jelenti, hogy a szekunder körben egy ideig folyik áram, de aztán ez nullára csökken. A primer körben ekkor a primer ellenállásnak megfelelő (

U_{0} / R_{1}

nagyságú) egyenáram fog folyni.
Egy másik határeset az ideális transzformátor, melyről a versenyfeladatban volt szó. Egy ,,jó minőségű transzformátorban'' a tekercsek között majdnem tökéletes az induktív kapcsolat,

M_{1}

és

M_{2}

tehát nagyon kicsi. Ez a mechanikai rendszerben annak felel meg, hogy mind a bal oldali, mind pedig a jobb oldali dugattyú tömege nagyon kicsi, a rendszerre jellemző többi (tömeg dimenziójú) mennyiség mellett elhanyagolható. Másrészt a tekercsek induktív ellenállásai (egy szokásosan működő, tehát terhelt transzformátornál) sokkal nagyobbak, mint az ohmos ellenállások (pl. egy izzó ellenállása). Az induktív ellenállás arányos az önindukciós együtthatóval, ezért ha az önindukciós együtthatók ,,elég nagyok'', éppen ezt az esetet kapjuk. A kölcsönös indukciós együttható (

M

, amely ideális transzformátor esetén az önindukciós együtthatók mértani közepe) szintén nagyon nagy kell legyen. A kétféle rendszer elemeinek fentebb megadott megfeleltetése szerint (ha az

A_{0}

keresztmetszetet

A_{1}

-gyel és

A_{2}

-vel azonos nagyságrendűnek választjuk) az

M

kölcsönös indukciós együttható akkor lesz nagy, ha az alsó dugattyú

m_{0}

tömegét igen nagynak választjuk.
Vajon mi történik akkor, ha a szinuszos váltófeszültségre kapcsolt ideális transzformátor szekunder körét egy kapcsolóval megszakítjuk? Ekkor a szekunderköri ellenállás végtelenné válik, a terheletlen transzformátor határesetét kapjuk. A mechanikai rendszerre vonatkoztatva ez azt jelenti, hogy a jobb oldali dugattyúnál a súrlódás végtelen naggyá válik. Ilyenkor ‐ akármekkora is a folyadék többletnyomása ‐ a jobb oldali dugattyú nem mozdulhat meg; olyan, mintha az a cső egy merev falban végződne. Így a folyadékot csak két dugattyú választja el a külvilágtól, ezek a térfogatmegmaradás miatt együtt (egymással arányos sebességgel) kell mozogjanak. Másrészt viszont a külső erő által létrehozott nyomáskülönbség az igen nagy tömegű alsó dugattyút csak alig tudja megmozdítani, és emiatt a bal oldali dugattyú is csak nagyon picit mozoghat.
Hogyan néz ki ugyanez az analóg elektromos rendszerben, a transzformátornál? A terheletlen transzformátornál a nagy indukciós együtthatójú tekercsen és az ellenálláson átfolyó primerköri áram sokkal kisebb lesz, mint a tekercs nélküli, csak ellenállást tartalmazó áramkörben: az induktivitás fojtótekercsként működik. Ez volt a harmadik,

(c)

lehetőség az Eötvös-verseny 3. feladatában. Ott azonban a transzformátor nem maradt terheletlen, a szekunder kört egy izzóval terheltük, melynek ellenállása összemérhető volt a primer ellenállással, és szintén elhanyagolható a tekercsek induktív ellenállásaihoz képest. A hidraulikus rendszerben ekkor az alsó dugattyú igen nagy tömege miatt alig mozdul meg, a jobb oldali és a bal oldali viszont egymással ,,szinkronban'' mozog. Tömegük elhanyagolható, így az erő változására pillanatszerűen beállnak a kicsiny súrlódási együtthatók által meghatározott sebességekre. A külső erővel gyakorlatilag csak a súrlódási erők tartanak ,,egyensúlyt'', ezért a két dugattyú szinuszosan változó sebessége nemcsak egymással, de a külső erővel is azonos fázisú kell legyen.
Innentől kezdve a feladat roppant egyszerűen megoldható. Felírhatjuk a térfogatmegmaradás egyenletét az alsó dugattyú kihagyásával:

A_{1} v_{1} + A_{2} v_{2} = 0

, továbbá Newton II. törvényét mindkét dugattyúra:

\begin{matrix} F - A_{1} Δ p - k_{1} v_{1} = 0, - A_{2} Δ p - k_{2} v_{2} = 0. \end{matrix}

Az eredetileg felírt differenciálegyenletekkel szemben ezek közönséges algebrai egyenletek, így elemi matematikával egyszerűen megoldhatók:

\begin{matrix} v_{1} = F \frac{n^{2}}{k_{1} n^{2} + k_{2}}, v_{2} = - F \frac{n}{k_{1} n^{2} + k_{2}}, \end{matrix}

ahol

n = \frac{A_{2}}{A_{1}}

. A mechanikai mennyiségeket a megfelelő elektromosra kicserélve és a versenyfeladatban szereplő számarányokat

(N = 3

R = R_{2} = 4 R_{1})

felhasználva kiszámíthatjuk az áramerősségek abszolút értékeit:

\begin{matrix} I_{1} & = \frac{U N^{2}}{R_{1} N^{2} + R_{2}} = \frac{N^{2}}{\frac{R_{1}}{R_{2}} N^{2} + 1} \frac{U}{R} = \frac{36}{13} \frac{U}{R}, \\ I_{2} & = \frac{U N}{R_{1} N^{2} + R_{2}} = \frac{N}{\frac{R_{1}}{R_{2}} N^{2} + 1} \frac{U}{R} = \frac{12}{13} \frac{U}{R} . \end{matrix}

Ebből a primer- illetve a szekunderköri izzókra eső feszültség:

\begin{matrix} U_{1} = I_{1} \frac{R}{4} = \frac{9}{13} U, U_{2} = I_{2} R = \frac{12}{13} U . \end{matrix}

Látszik, hogy az összes izzó tűrhetően ég, tehát az első

(a)

válasz volt a helyes.

¹3. feladat: Egy jó minőségű transzformátor szekunder tekercsének menetszáma háromszorosa a primer tekercsének. Ezt a trafót az ábra szerint hálózati váltóáramú feszültségforrásra kapcsoljuk a következő módon: A primer körbe egymással párhuzamosan iktatunk be öt egyforma, a hálózati feszültségre méretezett izzó közül négyet, az ötödiket a szekunder körbe kötjük. Mi történik a

K

kapcsoló zárása után?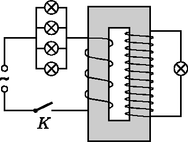

a)

Mindegyik izzó tűrhetően ég.

b)

A primer körbeli négy izzó szépen ég, az ötödik legfeljebb pislákol.

c)

A szekunder körbeli izzó egy pillanat alatt kiég, utána a primer körbeli izzók sem világítanak, mivel a primer tekercs fojtótekercsként hat.
Melyik a helyes válasz? (A részletes megoldást lásd múlt havi számunkban. ‐ A szerk.)