Cím:	Emelt szintű gyakorló feladatsor
Szerző(k):	Meszlényiné Róka Ágnes
Füzet:	2008/április, 202 - 203. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Oldjuk meg az alábbi egyenleteket: (11 pont)   2. Egy 32 lapos magyar kártyából 2 lapot húzunk. A húzás sorrendjét nem vesszük figyelembe. $a)$ Hány különböző lappárunk lehet? $b)$ Hány olyan lappár van, amelyben van makk? $c)$ A teljes kártyacsomagban hány különböző sorrendben lehetnek a piros lapok? $d)$ Mekkora a valószínűsége annak, hogy a megkevert teljes kártyacsomagban az első két helyen nincs piros lap?  (12 pont)   3. Egy vállalatnál jutalomosztáskor a jutalom összegét hat ember között $1:2:3:4:5:5$ arányban akarják szétosztani. Időközben kiderült, hogy az egyik dolgozó, aki a pénz 25%-át kapta volna, nem tett eleget a követelményeknek. Ekkor a neki szánt 225 000 Ft-ot úgy szerették volna szétosztani az öt ember között, hogy a kiosztott összegek egymás közötti aránya ne változzon meg. Mekkora összeget kap az öt ember külön-külön?  (14 pont)   4. Egy 10 egység oldalú négyzet $A$ csúcsa az origó, egyik oldalának meredeksége pedig 2. A négyzet az $x$ tengely felett helyezkedik el. $a)$ Adjuk meg a négyzet csúcsainak koordinátáit pontosan. $b)$ Tükrözzük a négyzetet az $x$ tengelyre. Mik lesznek a tükrözött négyzet csúcsainak koordinátái? $c)$ Mekkora a területe a koordinátatengelyekkel párhuzamos oldalú legkisebb téglalapnak, amelyet a két négyzet köré írtunk?  (14 pont)   II. rész   5. Adott egy $O$ középpontú 5 cm sugarú kör. Legyen a kör $AB$ átmérőjének $B$ ponton túli meghosszabbításán $B$-től 5 cm-re a $C$ pont. Ebből a pontból húzzunk érintőt a körhöz, ezen az érintési pont legyen $E$. $a)$ Igazoljuk, hogy az $ACE$ háromszög egyenlő szárú. $b)$ Számítsuk ki az $ACE$ háromszög oldalainak hosszát, szögeinek nagyságát. $c)$ Mekkora az $ACE$ háromszög területe? $d)$ Számítsuk ki az $ACE$ háromszögbe írható kör sugarának a pontos értékét.  (16 pont)   6. $a)$ Oldjuk meg a következő egyenletet: $2\cdot {\left(\frac{1}{4}\right)}^{3x}-{\left(\frac{1}{8}\right)}^{x-1}=384$. 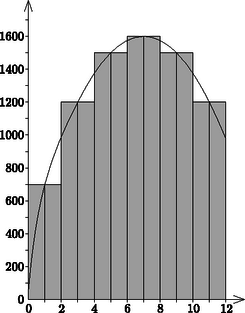$b)$ Van-e valós megoldása a $2\text{log}{}_{\frac{1}{4}}3x-\text{log}{}_{\frac{1}{4}}\left(x-1\right)=a$ egyenletnek, ha az $a$ paraméter nemnegatív valós szám?  (16 pont)   7. Az ábrán egy útszakaszon éjféltől délig elvégzett forgalomszámlálás eredményét látjuk. A vízszintes tengelyen az órákat, a függőlegesen százasokra kerekítve az elhaladó kocsik számát ábrázoltuk.     A forgalomszámláló kétóránként összesítette az ott elhaladó járműveket, és az így kapott adatokat egy-egy órára átlagolva oszlopdiagramon ábrázolta. (Az oszlopok területének mérőszáma az adott időintervallumban elhaladó kocsik számát adja.) Az ábrázolás után észrevette, hogy az egymás mellett fekvő azonos magasságú oszlopok felső vízszintes szakaszainak hat felezőpontja illeszkedik egy parabolára (lásd az ábrán). Szerinte ez a parabola valóságosabban mutatja az adott útszakasz forgalmának változását a megadott időben. $a)$ Hány autó haladt el a vizsgált útszakaszon az adott időben a diagram szerint? $b)$ Ha az autók számát nem az előbbi módon számoljuk, hanem a parabola alatti területtel közelítjük, akkor mit kapunk eredményül?  (16 pont)   8. Egy matematika versenyen 30 feladatot tűztek ki. András jó megoldásainak száma 16, míg Balázsé 14. Megállapították, hogy 7 olyan feladat volt, amelyiket mindketten jól oldottak meg. $a)$ Hány olyan feladat volt, amelyikkel egyikőjük sem boldogult? $b)$ Dénes, aki szintén részt vett a versenyen, megállapította, hogy 5 olyan feladat van, melyeket mindhárman jól megoldottak. Dénes egyeztette megoldásait Andrással, majd Balázzsal, rájöttek, hogy Andrással 8, Balázzsal 9 közös jó megoldásuk van. Végül azt is észrevették, hogy mindegyik feladatra legalább az egyikőjük jó megoldást adott. Kinek lett közülük a legtöbb jó megoldása? $c)$ Véletlenszerűen kiválasztunk a 30 feladatból egyet. Mennyi a valószínűsége, hogy pont ketten adtak rá jó megoldást?  (16 pont)   9. Az $x^2+\left(3p-2\right)x-\left(7p+2\right)=0$ egyenlet két gyöke nem negatív, akkor tekintsük úgy a két számot, mintha egy-egy kocka élének a hosszát jelentené. Határozzuk meg a $p$ paraméter értékét úgy, hogy a felszínösszeg minimális legyen.  (16 pont)