Kezdőlap


Cím:	Ízelítő a Fermat‐Torricelli problémakörből
Szerző(k):	Szmerka Gergely
Füzet:	2008/április, 194 - 201. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Pierre de Fermat 1643-ban tett feljegyzései között található a következő feladat: Adott három pont a síkon. Keressük azt a pontot, melynek távolságösszege e háromhoz minimális. Annak ellenére, hogy Fermat találta ki ezt az egyszerűnek tűnő feladatot, ő maga nem adott rá megoldást, nem foglalkozott sokat vele. Azonban ahhoz, hogy ez a geometriai probléma egész problémakörré növekedjen, Fermat megtette az első lépést: a XVII. századi tudományos élet szokásai szerint útjára bocsátotta, vagyis levélben elküldte egyik kortársának, a híres Mersenne-nek. A feladat aztán Mersenne közvetítésével eljutott Torricellihez, Vivianihoz Firenzébe és Cavalierihez Bolognába. Ők voltak az elsők, akik megoldásokat adtak a feladatra. Később aztán sokan foglalkoztak a problémával, annak általánosításával és mechanikai vonatkozásaival. A neves és tekintélyes Steiner is írt vázlatokat ezzel kapcsolatban. (Szokás ezt a feladatot Steiner feladatának is nevezni.) Az alábbiakban a viszonylag terjedelmes problémakörből szeretnék ízelítőt adni.
A feladatban keresett pontot a továbbiakban $P_{{min}_{}^{}}$ -nek vagy a három adott pont Fermat‐Torricelli pontjának fogom nevezni. Az első megoldás Torricelli nevéhez fűződik, melynek kiegészített változatát úgy nevezik, hogy

Torricelli tétele

1. eset: Ha az

A

B

C

pontok által meghatározott háromszög minden szöge

< 120^{\circ}

, akkor a

P_{{min}_{}^{}}

a háromszög izogonális pontja

(P_{iz})

, vagyis amely pontból a háromszög minden oldala egyenlő szögben látszik.

2. eset: Ha az

A

B

C

pontok által meghatározott háromszögnek van egy

120^{\circ}

-nál nagyobb vagy azzal egyenlő szöge, akkor

P_{{min}_{}^{}}

ennek a szögnek a csúcsa.

Meg kell említeni, hogy Torricelli pusztán az 1. esettel foglalkozott. Tekintve, hogy a 2. eset Cavalierinél fordult elő először, ezt Cavalieri változatának is szokták nevezni. Az első eset másik elnevezése: lebegő eset, a másodiké pedig: kötött eset. (Ez a

P_{{min}_{}^{}}

-nek az

A

B

C

pontokhoz viszonyított elhelyezkedését szemlélteti.)
Az itt következő bizonyítások első csoportja nem foglalkozik a Fermat‐Torricelli pont létezésének igazolásával.

Az 1. eset bizonyítása: A bizonyítás elején feltesszük, hogy egyértelműen létezik ez a

P_{{min}_{}^{}}

pont. Tekintsük azt az

e

ellipszist, amelynek fókuszpontjai

A

és

B

, és illeszkedik a

P_{{min}_{}^{}}

pontra, továbbá azt a

k

kört, amelynek középpontja a

C

pont és illeszkedik a

P_{{min}_{}^{}}

pontra (1. ábra).

1. ábra

P_{{min}_{}^{}}

pont a

k

és az

e

érintési pontja kell legyen. Ugyanis, tegyük fel indirekt, hogy a

P_{{min}_{}^{}}

a két alakzat (egyik) metszéspontja. Ekkor a

P_{{min}_{}^{}}

ponttal a

k

körön az ellipszis egy belső pontjába (

P'

-be) mozdulva azt kapnánk, hogy:

A P_{{min}_{}^{}} + B P_{{min}_{}^{}} > A P' + B P'

, míg

C P_{{min}_{}^{}} = C P'

. (Ugyanez a helyzet állna elő, ha az ellipszisen mozognánk a kör belseje felé.) Ez ellentmondás.
Az érintési pontban meghúzva a két alakzat közös érintőjét adódik, hogy

A P_{{min}_{}^{}} C ∢ = B P_{{min}_{}^{}} C ∢

, mivel, az ellipszis fokális tulajdonságának értelmében, az érintő felezi az adott pontba húzott rádiuszvektorok szögét, és a

k

kör érintője merőleges az adott pontba húzott sugárra. De, ha nem a

C

, hanem a

B

vagy az

A

pont körül rajzoljuk a kört, akkor másik két szög egyenlőségét kapjuk meg. Tehát:

A P_{{min}_{}^{}} C ∢ = B P_{{min}_{}^{}} C ∢ = A P_{{min}_{}^{}} B ∢

□

Torricelli és Cavalieri e tétel alapján mindjárt adott egy eljárást a

P_{{min}_{}^{}}

pont megszerkesztésére a lebegő esetre.

P_{{min}_{}^{}}

A B C

háromszög oldalai fölé kifele rajzolt egyenlő oldalú háromszögek körülírt köreinek közös metszéspontja (2. ábra).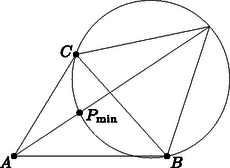

2. ábra

Hasonló szerkesztési módszert adott Simpson: Ha az

A B C

háromszög oldalai fölé kifelé egyenlő oldalú háromszögeket emelünk, akkor ‐ az ,,új'' pontokat

A'

B'

C'

-vel jelölve ‐ a

P_{{min}_{}^{}}

pont az

A A'

B B'

C C'

szakaszok metszéspontja (3. ábra).

3. ábra

Továbbá

\begin{matrix} A A' = B B' = C C' = A P_{{min}_{}^{}} + B P_{{min}_{}^{}} + C P_{{min}_{}^{}} . \end{matrix}

A körülírt körök segítségével való szerkesztést Viviani is ismerte, de adott egy olyan eljárást is, amely ennek és Simpson szerkesztésének az összekapcsolásaként is felfogható.
Viviani nevéhez fűződik az alábbi tétel általánosabb változata.

Viviani tétele az egyenlő oldalú háromszögekre

Ha egy szabályos

A B C

háromszög egy tetszőleges belső

P

pontjából merőlegeseket állítunk az oldalakra, akkor a

P T_{1} + P T_{2} + P T_{3}

összeg állandó és egyenlő az

A B C

háromszög magassainak hosszával, ahol

T_{1}

T_{2}

T_{3}

P

pontból az oldalakra bocsátott merőlegesek talppontjai.

Bizonyítás.

\begin{matrix} T_{A B C ▵} = A B \cdot m = T_{A B P ▵} + T_{B C P ▵} + T_{A P C ▵} = \\ = A B \cdot P T_{1} + B C \cdot P T_{2} + A C \cdot P T_{3} = A B \cdot (P T_{1} + P T_{2} + P T_{3}) . □ \end{matrix}

Úgy is szokták fogalmazni ezt a tételt, hogy az egyenlő oldalú háromszög rendelkezik a Viviani‐Steiner tulajdonsággal.

Viviani első bizonyítása Torricelli tételére

Viviani is csak az első esetet bizonyította, indirekt úton: Tegyük fel, hogy nem az izogonális pont a

P_{{min}_{}^{}}

, hanem valamely másik

P'

belső pont, vagyis

\exists P' \in A B C ▵

P' \neq P_{iz}

, amelyre

\begin{matrix} P_{iz} A + P_{iz} B + P_{iz} C \geq \\ \geq P' A + P' B + P' C, \end{matrix}

ahol

P_{iz}

A B C

háromszög izogonális pontja (4. ábra). Tekintsük azt az egyenlő oldalú

A' B' C'

háromszöget, amelynek oldalai rendre merőlegesek az

A P_{iz}

B P_{iz}

C P_{iz}

szakaszokra. Legyenek továbbá a

T_{A}

T_{B}

T_{C}

pontok a

P'

pontból az

A' B' C'

háromszög oldalaira bocsátott merőlegesek talppontjai. Ekkor Viviani tétele alapján felírhatjuk, hogy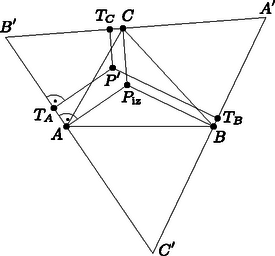

\begin{matrix} P_{iz} A + P_{iz} B + P_{iz} C = P' T_{A} + P' T_{B} + P' T_{C} < P' A + P' B + P' C . \end{matrix}

Vagyis ellentmondásra jutottunk.

□

4. ábra

Viviani nevéhez kapcsolható egy másik bizonyítás is, amely az alábbi lemma alapján könnyen befejezhető.

A Viviani-lemma

Tekintsük az

S = {P_{1}, P_{2}, ..., P_{n}}

ponthalmazt, és azt a

P_{{min}_{}^{}}

pontot, amelyre a

\sum_{j = 1}^{n} P_{j} P

minimális, ha

P = P_{{min}_{}^{}}

, továbbá az

S' = {P_{1}', P_{2}', ..., P_{n}'}

ponthalmazt és a

P'_{{min}_{}^{}}

pontot, amelyre

\sum_{j = 1}^{n} P_{j}' P

minimális, ha

P = P'_{{min}_{}^{}}

. Ha (minden

j

-re)

P_{j}'

P_{{min}_{}^{}} P_{j}

szakasz pontja, akkor

P'_{{min}_{}^{}} = P_{{min}_{}^{}}

, vagyis az

S

és az

S'

ponthalmaznak ugyanaz a Fermat‐Torricelli pontja.

Bizonyítás (

n = 3

pontra).

P_{1}

P_{2}

P_{3}

helyett

A

B

C

-vel fogom jelölni a pontokat. Nézzük tehát az

A B C

háromszöget, amelynek

P_{{min}_{}^{}}

a Fermat‐Torricelli-pontja. Legyen

A' \in P_{{min}_{}^{}} A

B' \in P_{{min}_{}^{}} B

C' \in P_{{min}_{}^{}} C

(5. ábra). Tegyük fel először, hogy az

A B C'

háromszögnek nem a

P_{{min}_{}^{}}

a Fermat‐Torricelli-pontja, vagyis

\exists P' \in A B C' ▵

, amelyre:

\begin{matrix} P_{{min}_{}^{}} A + P_{{min}_{}^{}} B + P_{{min}_{}^{}} C' > P' A + P' B + P' C' . \end{matrix}

Másrészt a

P'

pontra (is) tudjuk, hogy

\begin{matrix} P' A + P' B + P' C > P_{{min}_{}^{}} A + P_{{min}_{}^{}} B + P_{{min}_{}^{}} C, \end{matrix}

hiszen

P_{{min}_{}^{}}

A B C

háromszög Fermat‐Torricelli-pontja.

5. ábra

A két egyenlőtlenséget összeadva kapjuk:

\begin{matrix} P_{{min}_{}^{}} A + P_{{min}_{}^{}} B + P_{{min}_{}^{}} C' + P' A + P' B + P' C > \\ > P' A + P' B + P' C' + P_{{min}_{}^{}} A + P_{{min}_{}^{}} B + P_{{min}_{}^{}} C . \end{matrix}

Rendezve:

\begin{matrix} P_{{min}_{}^{}} C' + P' C > P' C' + P_{{min}_{}^{}} C . \end{matrix}

Tekintve, hogy

C' \in P_{{min}_{}^{}} C

szakasz:

\begin{matrix} P_{{min}_{}^{}} C = P_{{min}_{}^{}} C' + C C', \end{matrix}

ezért:

\begin{matrix} P_{{min}_{}^{}} C' + P' C > P' C' + P_{{min}_{}^{}} C' + C C' . \end{matrix}

Tovább egyszerűsítve:

\begin{matrix} P' C > P' C' + C C' . \end{matrix}

Ez azonban ellentmond a háromszög-egyenlőtlenségnek. Igazoltuk tehát, hogy az

A B C'

háromszögnek ugyanaz a Fermat‐Torricelli pontja, mint az

A B C

háromszögnek. Ugyanígy igazolhatjuk, hogy az

A B C

háromszögnek ugyanaz a Fermat‐Torricelli pontja, mint az

A B' C'

háromszögnek és az

A' B' C'

háromszögnek.
A bizonyítás szó szerint ugyanígy működik három helyett tetszőleges számú pontra, feltéve, hogy mindegyik ponthalmaznak egyértelműen létezik Fermat‐Torricelli-pontja.
Ezzel a lemmával igazolható Torricelli tételének első esete.

A Torricelli-tétel első esetének bizonyítása a Viviani-lemma segítségével

Tekintsük az

A B C

háromszöget. Szerkesszünk egy egyenlő oldalú

A' B' C'

háromszöget úgy, hogy az tartalmazza az

A B C

háromszöget és izogonális pontjaik egybeessenek. Az

A B C

háromszögnek belső pontja lesz az egyenlő oldalú háromszög izogonális pontja, amely egyben (a létezés egyértelműsége és a szimmetria miatt) az

A' B' C'

háromszög Fermat‐Torricelli pontja is. Ezek után alkalmazzuk a Viviani-lemmát az

A B C

és az

A' B' C'

háromszögre.

□

Tovább folytatva az első eset bizonyításainak sorát elérkezünk a sokak által legelegánsabbnak tartott bizonyításhoz, mely J. E. Hofmann nevéhez fűződik.¹

Egy forgatásos bizonyítás Torricelli tételének első esetére

Tekintsünk egy

A B C

háromszöget, amelynek minden szöge kisebb

120^{\circ}

-nál és benne egy tetszőleges

P

pontot. Forgassuk el

+ 60^{\circ}

-kal az

A

pont körül az

A P C

háromszöget. Így a

P

pont képe a

P'

pont lesz, a

C

pont képe pedig a

C'

(6. ábra). A forgatás távolságtartását felhasználva kapjuk, hogy

P' C' = P C

, illetve

A P = P P'

, hiszen az

A P P'

háromszög egyenlő szárú és a szárak által bezárt szöge

60^{\circ}

, tehát egyenlő oldalú is. Ezekből következően: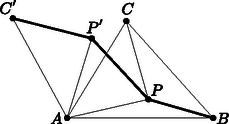

\begin{matrix} P A + P B + P C = P B + P P' + P' C' . \end{matrix}

Tehát az összeg, amelyet minimalizálni szeretnénk, megegyezik a

B P P' C'

töröttvonal hosszával. Ez nyilván pontosan akkor minimális, ha egybeesik a

B C'

szakasszal, mert a két végpontja (

B

és

C'

)

P

helyétől függetlenül mindig ugyanott van. Ebből következően a

P_{{min}_{}^{}}

pontnak és az elforgatott képének, a

P'_{{min}_{}^{}}

pontnak is a

B C'

szakaszon kell lennie (7. ábra). Tehát az

A P_{{min}_{}^{}} B ∢ = 120^{\circ}

(ez a szög az

A P_{{min}_{}^{}} P'_{{min}_{}^{}}

egyenlő oldalú háromszög egyik külső szöge.) Másrészt

P_{{min}_{}^{}}

rajta van az

A C C'

háromszög körülírt körén ‐ hiszen az

A P_{{min}_{}^{}} C' ∢ = A C C' ∢

, így mindkét szög csúcsa az

A C'

szakaszhoz tartozó

60^{\circ}

-os látószögköríven van, amely az

A C C'

háromszög körülírt köre ‐ tehát az

A P_{{min}_{}^{}} C = 120^{\circ}

. Ebből adódóan a

B P_{{min}_{}^{}} C ∢ = 120^{\circ}

6. ábra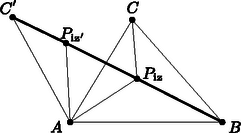

7. ábra

Megjegyzés: 1. Arra is hivatkozhattunk volna a kis háromszög elforgatása után, hogy a

P_{{min}_{}^{}}

pont az egyik Simpson egyenesre esik. Persze mindegy, hogy melyik csúcsot választjuk ki a forgatáshoz, ezért mindhárom csúcsra és mindhárom kis háromszögre hasonló eredményt kapunk. Vagyis a

P_{{min}_{}^{}}

a Simpson egyenesek metszéspontja.
2. Ez a bizonyítás ‐ az eddigiekkel szemben ‐ azt is megmutatta hogy a

P_{{min}_{}^{}}

pont létezik és egyértelmű.

A fenti bizonyításokkal alaposan körüljártuk Torricelli tételének első esetét, lássuk, hogy hogyan igazolható a második eset.

Egy forgatásos bizonyítás Torricelli tételének második esetére

Nem tudtam kideríteni, hogy ez a bizonyítás kinek a nevéhez fűződik, annyi azonban bizonyos, hogy a Skljavszkij‐Csencov‐Jaglom szerzőhármas könyvében bukkantam rá. Hofmann nem foglalkozott ezzel az esettel, annak ellenére, hogy a bizonyítás szinte lépésről lépésre ugyanúgy működik, mint az övé:
Tekintsük az

A B C

háromszöget, melynek egyik szöge, pl.

γ \geq

120

^{\circ}

, illetve az

A B C

háromszög egy tetszőleges belső pontját,

P

-t. Válasszuk ki az

A B C

háromszög egyik olyan csúcsát, amelynél

120^{\circ}

-nál kisebb szög van, pl. az

A

-t. Ha e pont körül elforgatjuk az

A P C

háromszöget

+ 60^{\circ}

-kal, akkor az

A P' C'

háromszöget kapjuk (8. ábra). A forgatás (előbb részletezett) tulajdonságai alapján azt kapjuk, hogy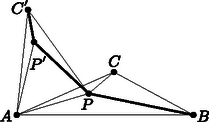

\begin{matrix} A P + B P + C P = B P + P P' + P' C' . \end{matrix}

Ez a

B P P' C'

töröttvonal hossza.

P

választásától függően csak a

P

és a

P'

pontok mozdulhatnak el,

P

viszont belső pont, tehát nem lehet az

A B C

háromszögön kívül. Így, a feltételeknek megfelelő

B

-t

C'

-vel összekötő töröttvonalak közül a

B C C'

lesz a legrövidebb. Ez pontosan akkor valósul meg, ha

P = C

□

8. ábra

Megjegyzés. A Skljavszkij‐Csencov‐Jaglom szerzőhármas könyvében található indoklás arra is, hogy külső pont miért nem lehet Fermat‐Torricelli pontja egy adott

A B C

háromszögnek. (Ez nyilván a könyv kérdésfeltevéséből is fakad, mert a feladat ott nem zárja ki a lehetséges megoldások közül a külső pontokat, míg sok korábbi szerző csak a belső vagy határpontokra szorítkozott a lehetséges megoldásokat illetően. Bár Fermat eredeti kérdése nem is háromszögre, hanem három pontra vonatkozott.) Lássuk a külső pontokat is! Vegyünk egy tetszőleges

A B C

háromszöget és egy tetszőleges külső pontját,

P

-t.

a)

P

beleesik az

A B C

háromszög valamelyik csúcsszögtartományába (pl.

γ

-éba), akkor az

\begin{matrix} A P + B P + C P > A C + B C \end{matrix}

teljesül (9. ábra).

9. ábra

b)

P

egyik csúcsszögtartományba sem esik bele, akkor (mondjuk) a

C P

szakasz elmetszi az

A B

oldalt, tehát a

P' = C P \cap A B

-re igaz, hogy

\begin{matrix} A P + B P + C P > A P' + B P' + C P' . \end{matrix}

Különös, hogy a második esetre egy másik, szintén forgatásos bizonyítás is van.

Sokolowsky (forgatásos) bizonyítása Torricelli tételének
második esetére

Tekintsük az

A B C

háromszöget, melynek valamelyik szöge (pl.

γ) \geq 120^{\circ}

. Forgassuk el a

C P A

háromszöget a

C

pont körül

μ

szöggel úgy, hogy az

A'

, a

C

és a

B

pontok egy egyenesre essenek.

γ \geq 120^{\circ}

, ezért

μ \leq 60^{\circ}

és

C P \geq P P'

(10. ábra). Ezt és a forgatás tulajdonságait kihasználva állíthatjuk, hogy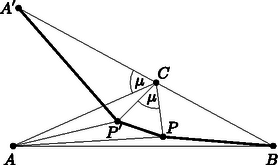

\begin{matrix} A P + B P + C P \geq B P + P P' + P' A' . \end{matrix}

B P P' A'

töröttvonal hossza akkor a legkisebb, ha a töröttvonal egybeesik a

B A'

szakasszal, vagyis ‐

P

helyzetét vizsgálva ‐ ha

P = C

10. ábra

Dörrie A diadalmas matematika című könyvében található egy bizonyítás Torricelli tételének második esetére.

Dörrie bizonyítása Torricelli tételének második esetére

Tekintsük az

A B C

háromszöget, melynek a

C

csúcsnál lévő szöge legyen

γ \geq 120^{\circ}

és egy tetszőleges

U

pontot a síkon.
Az alábbi módon igazolható, hogy

\begin{matrix} A C + B C < A U + B U + C U . \end{matrix}

Tekintsük az

A C U = ψ

és a

B C U = φ

szögeket. Az

U

pont eshet 1) az

A C B = γ

szög szárai közé, 2)

γ

csúcsszögének szárai közé, vagy 3)

γ

mellékszögének szárai közé. Ettől függően a következő összefüggések állapíthatók meg (11. ábra):
1)

ψ + φ = γ

,
2)

ψ + φ = 360^{\circ} - γ

, vagy
3)

φ - ψ = γ

11. ábra

Legyenek

F

és

G

U

pontból

A C

-re és

B C

-re bocsátott merőlegesek talppontjai. Akkor ezeknek a távolsága

C

-től:

\begin{matrix} F U = x = C U cos ψ \end{matrix}

és

\begin{matrix} G U = y = C U cos φ, \end{matrix}

ahol egy ilyen távolság, mondjuk

x

, pozitív vagy negatív aszerint, hogy

cos ψ

pozitív vagy negatív. Tehát mindegyik esetben:

\begin{matrix} A C = A F + x \end{matrix}

és

\begin{matrix} B C = B G + x, \end{matrix}

ezért:

\begin{matrix} A C + B C = A F + B G + x + y . \end{matrix}

Ebből következően:

\begin{matrix} x + y & = C U cos ψ + C U cos φ = \\ = C U (cos ψ + cos φ) = 2 \cdot C U \cdot cos \frac{ψ + φ}{2} cos \frac{ψ - φ}{2} . \end{matrix}

Mivel a fentiek szerint ezen egyenlet jobb oldalán álló két cosinus közül az egyiknek az abszolút értéke

cos \frac{γ}{2}

, ez azonban (

\frac{γ}{2} \geq 60^{\circ}

folytán) kisebb, mint

\frac{1}{2}

, a jobb oldal abszolút értéke legfeljebb

C U

. Következésképpen:

\begin{matrix} A C + B C \leq A F + B G + C U . \end{matrix}

Mivel továbbá az

A U F

és

B U G

derékszögű háromszögek, melyeknek

A F

és

B G

befogói kisebbek, mint az

A U

és

B U

átfogók, azért

\begin{matrix} A C + B C < A U + B U + C U . □ \end{matrix}

Irodalom

[1]	Heinrich Dörrie: A diadalmas matematika (Gondolat, Budapest, 1965.)

[2]	Y. S. Kupitz ‐ H. Martini: Geometric Aspects of the Generalized Fermat‐Torricelli Problem (in: Intuitive Geometry ‐ Bolyai Society Mathematical Studies, 6., Budapest, 1997, 55‐127. old.)

[3]	H. S. M. Coxeter: A geometriák alapjai (Műszaki Könyvkiadó, Budapest 1987.)

[4]	D. O. Skljarszkij ‐ N. N. Csencov ‐ I. M. Jaglom: Válogatott feladatok és tételek az elemi matematika köréből II. rész, 2. kötet: Geometriai szélsőértékfeladatok (Tankönyvkiadó, Budapest, 1973.)

[5]	Daniel Sokolowsky: A note on the Fermat‐Torricelli problem (in: American Mathematical Monthly, 83 (1976), 276. old.)

[6]	J. E. Hofmann: Elementare Lösung einer Minimumsaufgabe, Zeitschr. Math.-Naturwiss Unterr., 60 (1929), 22‐23.

¹A bizonyítást először 1929-ben J. E. Hofmann közölte, de Gallai is ugyanerre az eredményre jutott, tőle függetlenül.