|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész
1. Összeöntöttünk 5 kg 15 tömegszázalékos, 8 kg 20 tömegszázalékos és 12 kg 40 tömegszázalékos cukoroldatot. Az oldószer mindegyik esetben víz volt. Azóta beleborult 40 dkg cukor, elpárolgott a víz százaléka, és az egyensúly beállt.
Hány százalékos az oldat most?
Hányadrészét kell vízzel helyettesíteni az oldatnak, ha tömegszázalékos oldatot szeretnénk kapni? (11 pont)
Megoldás. Az összeöntés után keletkező 25 kg tömegű oldatban , azaz 7,15 kg oldott anyag, és 17,85 kg oldószer van. A cukor beleömlésével az oldott anyag tömege 7,55 kg-ra, a víz elpárolgásával az oldószer tömege 15,708 kg-ra változott.
Az oldat tehát tömegszázalékos.
kg tömegű oldatban 7,55 kg cukor van. Az kellene, hogy 2,3258 kg cukor legyen benne, mert a helyettesítés után az oldat mennyisége nem változik. Ezért kg cukrot ki kell venni belőle. Ezt a mennyiséget, egyenletes elkeveredést feltételezve megközelítőleg kg oldat tartalmazza. Ez a teljes oldat mennyiségének része.
Vagyis az oldat kb. 0,692 részét kell vízzel helyettesíteni.
2. A következő táblázat a földrészek lakosságának számát mutatja -ben.
a) Állapítsuk meg az adatsokaság átlagát, szórását.
b) Készítsünk diagramot a Föld lakosságának kontinensek szerinti eloszlásáról. (12 pont)
Megoldás. a) A kontinensek átlagos lakossága: 952,6˙ millió fő, a szórás közelítőleg: 1162,4 millió.
b) Az eloszlást jól szemléltethetjük például kördiagrammal. A körcikkekhez tartozó középponti szögeket a táblázat mutatja. (Természetesen bármilyen jól elkészített diagramm megfelel a feladat kérésének.)
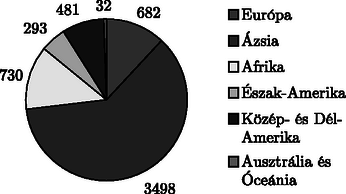 FöldrészKözéppontiszög (fok)Európa242,95Ázsia220,31Afrika245,98Észak-Amerika218,45Közép- és Dél-Amerika230,29Ausztrália és Óceánia222,02
3. a) Tudjuk, hogy p és 10p-1 pozitív prímszámok. Lehet-e prímszám a 10p+1?
b) Péter és Pál mindketten nagyon okosak. Egy alkalommal Péter azt mondta Pálnak:
‐ Az imént meglátogattak engem hárman. Az életkoruk összege néggyel több, mint a tiéd, az életkoruk szorzata a 35 négyzetének a duplája, és mindegyikük több, mint négyéves.
‐ Nem tudom a választ ‐ közölte rövid gondolkodás után Pál.
‐ Az egyik látogatóm idősebb nálam ‐ folytatta Péter a párbeszédet.
‐ Akkor tudom a választ ‐ mondta Pál.
Mennyi Péter és Pál közt a korkülönbség? (14 pont)
Megoldás. a) Ha p=3, akkor 10p-1=29, ami prímszám és 10p+1=31, ami szintén prímszám.
Ha p≠3 és prím, akkor 10p-1, amiről tudjuk, hogy prím és minimum 19 nem lehet osztható 3-mal. Nyilván 10p sem osztható hárommal, ezért 10p+1 osztható hárommal (három egymást követő egész szám közül pontosan egy osztható hárommal). Mivel 10p+1 osztható hárommal és nagyobb, mint 19 ezért nem lehet prím.
Tehát a feladat feltételei mellett kizárólag a p=3 esetén prímszám a 10p-1 és a 10p+1.
b) Pál kiszámolta, hogy 35 négyzetének a duplája 2450, ami 2⋅52⋅72 alakban bontható fel prímtényezőkre, és a következő módokon bontható a feltételeknek megfelelő, háromtényezős szorzatokra:
SzorzótényezőkSzorzatÖsszeg559824501085770245082510492450645143524505477502450647103524505271425245046
Mivel Pál ismeri a saját életkorát, ezért nyilván a vastagított két eset között nem tudott dönteni. Tehát Pál 60 éves. Mikor Péter azt mondta, hogy a látogatók egyike idősebb nála, és Pál ezután már tudott dönteni, ebből mi arra következtethetünk, hogy Péter 49 éves, hiszen ha ennél fiatalabb lenne, akkor Pál nem tudott volna dönteni, ha pedig idősebb lenne, akkor ellentmondásra jutnánk. Tehát Pál 11 évvel idősebb, mint Péter.
4. a) Adott a síkon 2007 darab olyan pont, amelyek közül semelyik három nem esik egy egyenesbe. Ezek közül három pont zöld. Tekintsük az összes olyan háromszöget, amelyeket a 2007 pont meghatároz. Hány olyan van ezek között, amelynek van zöld csúcsa?
b) Mutassuk meg, hogy a Fibonacci-sorozat bármely két szomszédos tagja relatív prím.
(A Fibonacci-sorozat képzési szabálya: a1=1; a2=1; an=an-1+an-2, minden n>2 esetén.) (14 pont)
Megoldás. b) Olyan háromszög, amelynek nincs zöld csúcsa (20043) darab van. Összesen (20073) darab háromszöget határoznak meg a pontok. Ezekből adódóan (20073)-(20043) darab olyan háromszög van, amelynek van zöld csúcsa.
a) Indirekt módon bizonyítunk. Tegyük fel állításunk ellenkezőjét, vagyis hogy a Fibonacci-sorozatnak van két olyan szomszédos tagja, melyek nem relatív prímek. Jelöljük őket a következőképpen: ak és ak-1. Feltevésünk alapján van olyan 1-nél nagyobb m egész szám, amelyre igaz, hogy m∣ak és m∣ak-1. Ebből az oszthatóságra vonatkozó összefüggések alapján következik, hogy m∣(ak-ak-1)=ak-2. Hasonló gondolatmenettel igazoljuk, hogy m∣ak-1 és m∣ak-2 ismeretében m∣ak-3. Véges sok lépés után eljutunk oda, hogy m∣a2=1 is igazolást nyer. Ez pedig ellentmondás. Tehát az eredeti állítás igaz.
II. rész
5. a) Oldjuk meg a következő egyenletet: 2x3-3x2+3x-1=0.
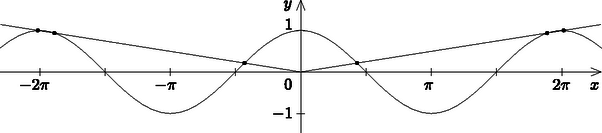
b) Hány megoldása van a cosx=|x|2π egyenletnek? (16 pont)
Megoldás. a) Rendezzük az egyenletet a következő alakra: x3-3x2+3x-1=-x3. Az x=0 nem megoldás, ezért oszthatunk x3-nal: (x-1)3x3=-1. Azaz x-1x=-1, amiből kapjuk, hogy x=12.
Ez valóban megoldása az eredeti egyenletnek.
b) Az egyenlet két oldalán álló függvények közös koordináta-rendszerben történő ábrázolása után megállapíthatjuk, hogy az egyenletnek pontosan 6 db gyöke van.
x=±2π megoldása az egyenletnek és mivel ebben a két pontban a cosx érintőjének meredeksége 0, még 4 megoldásnak kell lennie. A [-2π;2π] intervallumon kívül további megoldás nincs.
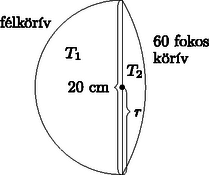
6. Az ábrán fából készült kerítésoszlopok keresztmetszetét látjuk. A 80 db kerítésoszlop mindegyike 3 méter hosszú, és 1 méteres darabjuk lesz a földben. A kerítésoszlopoknak ezt a részét speciális folyadékkal itatják át, hogy tartósabbak legyenek.
a) Mennyi folyadékra van szükség, ha 1m3 faanyag 2,5 liter folyadékot ,,nyelt el''?
b) Mennyi festékre van szükség a már felállított kerítésoszlopok festéséhez, ha a használt festékből 1 kg 4m2-re elegendő? (16 pont)
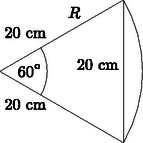
Megoldás. Használjuk a vázlatrajzok jelöléseit.
a) A félkör területe: T1=r2π2≈157,08. A 60∘-os középponti szögű körszelet területe: | T2=16R2π-R2sin60∘2≈36,23. |
A metszetidom területe: T=T1+T2=193,31.
Egy (földben lévő) kerítésláb magassága 1 m, térfogata: V=T⋅m=193,31⋅100≈19331cm3, azaz kb. 0,0193 m3.
A szükséges folyadékmennyiség: 80⋅V⋅2,5=80⋅0,0193⋅2,5=3,9. Azaz kb. 3,9 liter folyadék szükséges.
b) A félkör körívhossza: k1=2rπ2≈31,42. A körszelet körívhossza: A metszetidom kerülete: k=k1+k2≈52,36. A befestendő test magassága: m'=200. A befestendő felszín: | A=80⋅T+80⋅k⋅m'≈853225cm2, |
ami kb. 85,3 m2.
A szükséges festékmennyiség: A4≈21,33 kg.
7. Hajótöröttek egy lakatlan, növényzet nélküli szigeten azt tervezik, hogy a viharban zátonyra futott eredeti vitorlás hajójuk darabjaiból új, kisebb hajót építenek. A vihar az árbocot véletlenszerűen három darabra törte. Ha az eredeti 40 m hosszú árbocnak maradt egy legalább 20 m-es darabja, akkor a hajó megépíthető. Mi a valószínűsége annak, hogy amikor visszaúsznak a hajóroncshoz, találnak ilyen darabot? (16 pont)
Megoldás. A feladat lényegében a következő: Ha az egységszakaszon véletlenszerűen kiválasztunk két pontot, melyek három részre osztják az egységszakaszt, akkor mi a valószínűsége annak, hogy keletkezik egy legalább 12 hosszúságú szakasz. A törési helyek kiválasztását ezek szerint úgy tesszük meg, hogy a 40 métert egységnek, a 20 métert pedig 12-nek tekintve, a koordinátasík egységnégyzetének (x;y) koordinátájú pontját választjuk ki véletlenszerűen. A probléma komplementerének valószínűségét fogjuk meghatározni, nevezetesen: Ha az egységszakaszon véletlenszerűen kiválasztunk két pontot, melyek három részre osztják az egységszakaszt, akkor mi a valószínűsége annak, hogy a keletkezett szakaszok egyike sem hosszabb 12-nél.
Két esetet különböztetünk meg:
I. x<y. Ekkor egyszerre a következő feltételeknek kell teljesülni: x<12, y-x<12, azaz y<x+12, továbbá 1-y<12, azaz y>12.
II. x>y. Ekkor egyszerre a következő feltételeknek kell teljesülni: y<12, x-y<12, azaz y>x-12, továbbá 1-x<12, azaz x>12.
A feltételeket teljesítő pontokat ábrázolva látszik, hogy a keresett valószínűség: p'=0,25.
Visszatérve az eredeti feladatra: p=1-p'=0,75 annak a valószínűsége, hogy a hajótöröttek találnak nekik megfelelő darabot.
8. Egy vállalattól 100 db henger alakú, 1m3 belső térfogatú, speciális fémlemezből kialakított zárt tartályt rendeltek. A megrendelő csak a térfogatot és az alakot határozta meg. Mekkora legyen a henger magassága, ha a vállalat a lehető legkevesebb anyagot szeretné felhasználni? (16 pont)
Megoldás. Keressük, hogy az 1m3 térfogatú henger felszíne mekkora magasság mellett lesz minimális. A szokásos jelölést használva a térfogat: V=r2πm=1, amiből r2=1πm. Ekkor a felszín: | A=2r2π+2rπm=21πmπ+21πm⋅πm=2m+2πm. |
Vagyis az A(m)=2m+2πm minimumát keressük.
Meghatározzuk a derivált zérushelyét: | A'(m)=-2m-2+π⋅m-12=0,vagyisπ⋅m-12=2m2. |
Ebből kapjuk, hogy Mivel a függvény második deriváltja ezen a helyen pozitív, azért m=4π3 esetén a felszínnek minimuma van.
Vagyis a henger magassága kb. 1,08 m.
9. A tengerpart mentén sík terepen állomásozó saját tüzérségét, és az ugyancsak a tengerpart menti sík terepen található ellenséges gyalogos hadtest helyzetét vizsgálja a hadvezér egy 480 m magas hegy tetejéről. A két hadtest látszólagos távolsága 71,2∘. A hadvezér a tüzérséget 6∘30', a gyalogságot 8∘ depressziószög alatt látja. Kiadja-e a matematikához jól értő hadvezér a tűzparancsot, ha tudja, hogy tüzérsége ágyúinak maximális lőtávolsága 4 km? (16 pont)
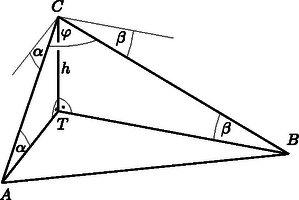
Megoldás. Elkészítjük a szöveg alapján a vázlatrajzot.
Az ábra szerint az A pontban van a gyalogság, B pontban van a tüzérség, és a C pontban tartózkodik a hadvezér. Az adatok: α=8∘, β=6∘30', φ=71,2∘, h=480 m.
Szögfüggvények alkalmazásával:
AC=hsinα≈3448,94;BC=hsinβ≈4240,16.
Alkalmazva a koszinusztételt: AB2=AC2+BC2-2⋅AC⋅BC⋅cosφ, ebből adódik, hogy AB≈4522 m.
Tehát a matematikához jól értő hadvezér nem fog tűzparancsot adni. |
 PDF | MathML
PDF | MathML