Kezdőlap


Cím:	A lécháromszög mint fizikai inga
Szerző(k):	Légrádi Imre
Füzet:	2008/február, 108 - 112. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Lapunkban korábban (lásd a 2002. évi 5. szám 229. old.) már foglalkoztunk az ,,egydimenziós háromszögek'' (vagyis a háromszög oldalai mentén koncentrált tömegeloszlású testek) súlypontjának meghatározásával. Az ott közöltek alkalmazásaként az alábbiakban az ilyen háromszögből készült fizikai inga lengésidejét számítjuk ki. A rövidség kedvéért nevezzük lécháromszögnek az ingaként felfüggesztett alakzatot, és vizsgáljuk az alábbi feladatot: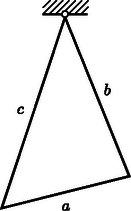
Egyenletes keresztmetszetű és anyagsűrűségű $a \leq b \leq c$ hosszúságú vékony lécekből merev háromszöget készítünk, és azt az egyik, mondjuk a legrövidebb oldallal szemközti csúcsában a háromszög síkjára merőleges tengelyre ingaként felfüggesztjük (1. ábra). Határozzuk meg ennek a fizikai ingának kis kitérések esetén érvényes lengésidő-képletét!

1. ábra

A fizikai ingák lengésidejének képletében a

\begin{matrix} \frac{Θ}{M g s} \end{matrix}

kifejezés szerepel; ebben

Θ

az ingatestnek a forgástengelyre vonatkozó (teljes, a három léc összesített) tehetetlenségi nyomatéka,

M

az össztömeg,

s

pedig az inga

S

tömegközéppontjának (súlypontjának) a tengelytől mért távolsága.
Számítsuk ki először

Θ

-t! Esetünkben a két hosszabb oldal egy-egy vége illeszkedik a tengelyre, tehát együttes tehetetlenségi nyomatékuk (ha a léc hosszegységre eső tömegét

ϱ

-val jelöljük):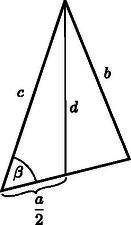

\begin{matrix} Θ_{b} + Θ_{c} = \frac{1}{3} m_{b} \cdot b^{2} + \frac{1}{3} m_{c} \cdot c^{2} = \frac{1}{3} ϱ (b^{3} + c^{3}) . \end{matrix}

A harmadik (legrövidebb) oldal tehetetlenségi nyomatékát a Steiner-tétel segítségével határozzuk meg. Ebben szükség van az oldal felezőpontja és a tengely

d

távolságára (2. ábra).

2. ábra

Írjuk fel a koszinusztételt először a teljes háromszögre, majd annak bal oldali felére úgy, hogy a

b

, illetve a

d

szakaszokat fejezzük ki. Mindkét összefüggésben szerepel

cos β

, ezt kiküszöbölve kapjuk a keresett

d

szakasz négyzetére:

\begin{matrix} d^{2} = \frac{2 b^{2} + 2 c^{2} - a^{2}}{4} . \end{matrix}

Ennek felhasználásával már felírhatjuk az egész lécháromszög tehetetlenségi nyomatékának képletét:

\begin{matrix} Θ & = & \frac{1}{3} ϱ (b^{3} + c^{3}) + \frac{1}{12} ϱ a \cdot a^{2} + ϱ a \cdot \frac{2 b^{2} + 2 c^{2} - a^{2}}{4} = \\ = & \frac{2 b^{3} + 2 c^{3} - a^{3} + 3 a b^{2} + 3 a c^{2}}{6} ϱ . \end{matrix}

Az inga össztömege az oldalak tömegének összegeként számítható:

\begin{matrix} M = (a + b + c) ϱ . \end{matrix}

Belátható (lásd pl. az idézett cikket a KöMaL 2002. évi 5. számában), hogy egy lécháromszög

S

súlypontja a háromszög

P

Q

és

R

oldalfelező pontjai által meghatározott háromszög belső szögfelezőinek metszéspontjában, vagyis az ide beírható kör középpontjában van (3. ábra). (Az eredeti háromszög szögei a szokásos jelekkel: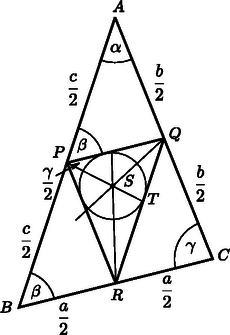

α

β

és

γ

3. ábra

s

szakasz meghatározásához tekintsük azt a négyszöget, amelynek csúcsai a következők: az

S

súlypont, a

b

oldal

Q

felezőpontja, a lengési tengelyt képező

A

háromszög-csúcspont, és végül a

c

oldal

P

felezőpontja (4. ábra).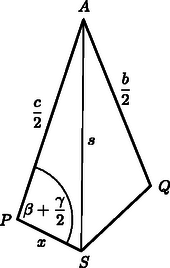

4. ábra

A vizsgált négyszögben az

A S

átlóra vonatkozó koszinusztétel:

\begin{matrix} s^{2} = \frac{c^{2}}{4} + x^{2} - 2 \cdot \frac{c}{2} \cdot x \cdot cos (β + \frac{γ}{2}) . \end{matrix}

Ebben

x

az eredeti háromszög oldalfelező pontjai által képzett kis háromszög egyik belső szögfelezőjének része (azon darabja, amely a

c

oldal

P

felezőpontjától a kis háromszögbe beírható kör középpontjáig, vagyis esetünkben a léckeret

S

fizikai súlypontjáig tart). Nagyságát meg tudjuk határozni abból, hogy a háromszög szögfelezőjének hossza ismert módon (lásd pl. Lukács Ottó, Scharnitzky Viktor: Érdekes matematikai feladatok VI., Középiskolai szakköri füzetek, 1975. 108. feladat) kiszámítható az oldalak hosszából. A számolás során felhasználjuk a szögfelező-tételt, amelyben a

c

oldalnak a szögfelelző által szétválasztott két része,

c_{1}

és

c_{2}

szerepel (5. ábra).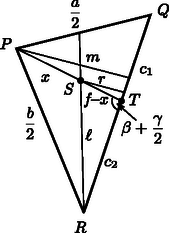

5. ábra

Jelen esetben a kis háromszög

\frac{a}{2}

és

\frac{b}{2}

hosszúságú oldalai által közrefogott szögfelezőről van szó, amelynek hossza tehát (az idézett tétel szerint):

\begin{matrix} f = \frac{\sqrt[]{a b {(a + b)}^{2} - a b c^{2}}}{2 (a + b)} . \end{matrix}

Az 5. ábrán szerepel még az oldalfelező pontok által meghatározott kis háromszögbe írható kör

r

sugara, illetve a

\frac{c}{2}

hosszúságú oldalhoz tartozó

m

magasság. A magasság és a szögfelező, valamint

r

és a szögfelező mellette levő része két derékszögű háromszöget alkot; ezek hasonlósága miatt fennáll, hogy

\begin{matrix} \frac{f - x}{f} = \frac{r}{m} . \end{matrix}

Ha az eredeti (

a

b

és

c

oldalú) nagy háromszög területe

t

, akkor a kis háromszögé

\frac{t}{4}

. Héron képletét használva kapjuk, hogy

\begin{matrix} \frac{r}{m} = \frac{c}{a + b + c}, \end{matrix}

s evvel:

\begin{matrix} x = f \cdot \frac{a + b}{a + b + c} = \frac{\sqrt[]{a b {(a + b)}^{2} - a b c^{2}}}{2 (a + b + c)} . \end{matrix}

A 4. ábrán látható négyszög átlója

s

hosszának kiszámításához szükségünk van a

β + \frac{γ}{2}

szög koszinuszának értékére is. Az 5. ábrán az

S T R ∢

a 4. ábrán látható

A P S ∢

váltószöge, tehát egyenlőek. Az

T R P

háromszög

R S

szögfelezőjének

ℓ

hossza ugyanúgy határozható meg, ahogyan korábban

x

-et kaptuk. A kiszámított

ℓ

értéket az

S T R

háromszögre felírt

\begin{matrix} ℓ^{2} = {(f - x)}^{2} + c_{2}^{2} - 2 (f - x) c_{2} \cdot cos (β + \frac{γ}{2}) \end{matrix}

koszinusztételbe helyettesítve, majd abból a kívánt koszinusz értéket kifejezve:

\begin{matrix} cos (β + \frac{γ}{2}) = \\ = \frac{c^{2} [a b {(a + b)}^{2} - a b c^{2}] + b^{2} c^{2} {(a + b + c)}^{2} - {(a + b)}^{2} [b c {(b + c)}^{2} - a^{2} b c]}{2 (a + b + c) b c^{2} \sqrt[]{a b {(a + b)}^{2} - a b c^{2}}} . \end{matrix}

Ezzel (a már felírt koszinusztételből) a súlypont és a tengely keresett távolságára:

\begin{matrix} s = \frac{\sqrt[]{c {(a + b + c)}^{2} (c - b) + a (b - c) [{(a + b)}^{2} - c^{2}] + [{(b + c)}^{2} - a^{2}] {(a + b)}^{2}}}{2 (a + b + c)}, \end{matrix}

a lengésidő képlete pedig (algebrai átalakítások után):

\begin{matrix} T = 2 π \sqrt[]{\frac{2 (b^{2} + c^{2} - b c) + a (b + c) - a^{2}}{3 g} \sqrt[]{\frac{a + b + c}{b^{3} + c^{3} - a^{3} + a (2 b^{2} + 2 c^{2} - b c)}}} . \end{matrix}

A kapott ‐ meglehetősen terjedelmes ‐ lengésidő-képletet (amely akkor is érvényes, ha nem

a

a legrövidebb oldal) érdemes néhány speciális esetben a fentiektől független, önálló számítással is ellenőrizni. Ilyen speciális eset, amikor

b = c

, vagyis egyenlőszárú háromszög képezi az ingát (

0 < a < 2 b

). Egy ilyen inga súlypontjának helye közvetlen számítással úgy kapható, hogy a két szár együttes

2 b ϱ

tömegét az

a

alaphoz tartozó

m

hosszúságú magasságvonalra, annak felezőpontjába helyezzük, az alapvonal teljes

a ϱ

tömegét pedig a magasságvonal alsó végpontjába koncentrálva képzeljük el. A lécháromszög súlypontja a magasság felezőpontja alatt bizonyos

x

távolságban lesz, s ezt a távolságot a szokásos nyomatéki egyenletből számíthatjuk ki:

\begin{matrix} 2 b ϱ \cdot x = a ϱ (\frac{m}{2} - x) . \end{matrix}

Ebből

\begin{matrix} x = \frac{m a}{2 (2 b + a)}, \end{matrix}

vagyis a súlypont és a forgástengely távolsága

\begin{matrix} s = \frac{m}{2} + x = \frac{m}{2} + \frac{m a}{2 (2 b + a)} = m \cdot \frac{a + b}{2 b + a} . \end{matrix}

Az inga teljes tömege:

M = (a + 2 b) ϱ

. A rendszer tehetetlenségi nyomatéka a három léc tehetetlenségi nyomatékának összegeként számolható. A háromszög alapját képező lécdarabnak a rajta kívül fekvő tengelyre vonatkozó tehetetlenségi nyomatéka a Steiner-tétel alapján

\begin{matrix} Θ_{a} = \frac{1}{12} a ϱ \cdot a^{2} + a ϱ \cdot m^{2}, \end{matrix}

ahol (a Pitagorasz-tételt alkalmazva) a magasság négyzete

\begin{matrix} m^{2} = b^{2} - \frac{a^{2}}{4} . \end{matrix}

A háromszög szárait alkotó lécek tehetetlenségi nyomatéka a végpontjukon átmenő tengelyre vonatkoztatva:

\begin{matrix} Θ_{b} = Θ_{c} = \frac{1}{3} b ϱ \cdot b^{2}, \end{matrix}

a teljes lécháromszög tehetetlenségi nyomatéka pedig

\begin{matrix} Θ = Θ_{a} + Θ_{b} + Θ_{c} = 2 \cdot \frac{1}{3} b ϱ \cdot b^{2} + \frac{1}{12} a ϱ \cdot a^{2} + a ϱ \cdot m^{2} = \frac{4 b^{3} + 6 a b^{2} - a^{3}}{6} ϱ . \end{matrix}

Mindezek felhasználásával a lengésidő:

\begin{matrix} T = 2 π \sqrt[]{\frac{4 b^{3} + 6 a b^{2} - a^{3}}{3 g (a + b) \sqrt[]{4 b^{2} - a^{2}}}} = 2 π \sqrt[]{\frac{(2 b^{2} + 2 b a - a^{2}) \sqrt[]{2 b + a}}{3 g (a + b) \sqrt[]{2 b - a}}} . \end{matrix}

Az általános képletben

b = c

helyettesítést alkalmazva megkapjuk ugyanezt az eredményt, ezzel ellenőriztük egy speciális esetben az általános formula helyességét.
Ha ‐ mesterkélt módon ‐ még az

a = 0

,,oldalhosszal'' is számolunk, akkor két, szorosan egymás mellett elhelyezkedő lécdarab, vagyis egy

M

tömegű rúdinga esetét kapjuk, amelynek lengésideje:

\begin{matrix} T = 2 π \sqrt[]{\frac{Θ}{M g s}} = 2 π \sqrt[]{\frac{\frac{1}{3} M b^{2}}{M g \frac{b}{2}}} = 2 π \sqrt[]{\frac{2 b}{3 g}}, \end{matrix}

amit természetesen ‐ határesetben ‐ az általános képlet is visszaad.
Hasonlóan számíthatjuk ki egy szabályos lécháromszög lengésidejét is. Az általános képletből

a = b = c

helyettesítéssel, vagy a fizikai inga lengésidő-képletéből (a tömegközéppont helyzetének ismeretében, és a Steiner-tételt alkalmazva) adódik:

\begin{matrix} T = 2 π \sqrt[]{\frac{a \sqrt[]{3}}{2 g}} . \end{matrix}