Cím: A 2007. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):  Fleiner Tamás 
Füzet: 2008/február, 67 - 70. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd), Matematika, Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Egy kör mentén n>3 kártyát helyeztünk el úgy, hogy mindegyik kártyának a hátoldala látható. Egy lépésben három szomszédos kártyával az alábbi helycserét végezhetjük: a három közül az egyik szélső kártyát a másik szélső kártya helyére tesszük, a fennmaradó két kártyát pedig eggyel odébbtoljuk és megfordítjuk. Ilyen lépések sorozatával elérhető-e, hogy minden kártya a kiindulási helyére kerüljön és az előlapja legyen látható?

 
Megoldás. Állítjuk, hogy nem létezik a feladatban leírt lépéssorozat. Indirekt bizonyítunk: tegyük fel, hogy van ilyen. Figyeljük meg, hogy minden lépésben páros sok kártyát fordítunk meg, ezért a hátoldalukat mutató kártyák számának paritása sosem változik. Mivel kiinduláskor minden kártyának a hátoldala volt látható, a lépéssorozat végére pedig 0 ilyen kártya lett, a kör mentén elhelyezett kártyák száma páros. A kártyák helyét ezek szerint kiszínezhetjük feketére és fehérre úgy, hogy a színek felváltva következzenek a kör mentén. A helycsere szabályából adódóan ha egy kártyát egy lépésben megfordítunk, akkor a helyének a színe is megváltozik, ha pedig nem fordítjuk meg a kártyát a lépés során, akkor az ugyanolyan színű helyre kerül, mint amilyenen a lépés előtt volt. Ebből az következik, hogy ha egy kártya az eredeti helyére kerül egy lépéssorozat során, akkor annak szükségképpen a hátlapja (tehát nem az előlapja) látszik. Ez ellentmond az indirekt feltevésünknek, vagyis igazoltuk, hogy nem létezik a feladatban leírt lépéssorozat.  □
 
2. feladat. Bizonyítsuk be, hogy ha egy 2-vel kezdődő, egészekből álló (véges vagy végtelen) számtani sorozat bármely 2007 szomszédos tagja között van olyan, amely a többi 2006-hoz relatív prím, akkor bármely 2008 szomszédos tagja között van olyan, amely a többi 2007-hez relatív prím.
 
Megoldás. Jelölje d a szóban forgó számtani sorozat különbségét. Ha d páros, akkor a sorozat csupa páros számból áll. Egy ilyen sorozatra csak úgy lehet igaz a feladatban leírt tulajdonság, ha a sorozatnak legfeljebb 2006 tagja van. Ekkor persze a feladat az üreshalmaz eleméről állít valamit, tehát nincs mit bizonyítanunk.
Az érdekes eset az, amikor d páratlan. Tekintsük a sorozat 2008 egymást követő tagját, legyen ezek halmaza mondjuk H={a,a+d,a+2d,...,a+2007d}. Mivel d páratlan, azért a és a+2007d ellentétes paritásúak; jelölje p közülük a páratlant. Ekkor H∖{p} a vizsgált számtani sorozat 2007 szomszédos tagja, így a feltétel szerint valamelyikük (mondjuk q) relatív prím H∖{p} minden eleméhez. Állítjuk, hogy q teljesíti a feladat által megkívánt tulajdonságot, azaz q a H halmaz minden eleméhez relatív prím. Ehhez pedig csupán azt kell igazolnunk, hogy p és q relatív prímek.
Világos, hogy q páratlan, hiszen a H∖{p} sorozatnak van q-tól különböző páros tagja, amihez q relatív prím. Márpedig ha p és q páratlan tagjai egy páratlan különbségű számtani sorozatnak, akkor sorszámuk páros számmal különbözik, így r:=p+q2 is tagja a számtani sorozatnak. Ráadásul, mivel p a H ,,szélső'' eleme, r∈H∖{p} is teljesül. Ezért q és r relatív prímek a q választása miatt. Jelölje D a (páratlan) p és q számok legnagyobb közös osztóját. Világos, hogy D∣p+q és mivel D páratlan, azért D∣p+q2=r is teljesül. Azt kaptuk, hogy D közös osztója a relatív prím q és r számoknak. Ezt azt jelenti, hogy D=1, tehát p és q is relatív prímek. Nekünk pedig éppen ezt kellett igazolnunk.  □
 
Megjegyzés. Több dolgozatban szerepel, hogy a feladatban leírt tulajdonságú számtani sorozatok differenciája páratlan. Jóllehet ez az állítás nem igaz, az értékelés során ezt nem tekintettük komoly hibának, hiszen az ,,elnézett'' esetben a feladat állítása az üreshalmaz elemére vonatkozik. Felmerül azonban, hogy páratlan d esetén nincs-e vajon ugyanerről szó. Más szóval: létezik-e egyáltalán olyan legalább 2007 tagú számtani sorozat, ami megfelel a feladat feltételeinek. ,,Szerencsére'' a válasz igen: könnyen belátható, hogy ha d a 2-nél nagyobb és 1004-nél kisebb prímek szorzata, akkor a 2+d,2+2d,2+3d,... végtelen számtani sorozat bármely 2007 egymást követő tagja közül a középső relatív prím a többi 2006 tag bármelyikéhez.
 
3. feladat. Bizonyítandó, hogy a sík rácspontjainak tetszőleges véges H halmazából kiválasztható olyan K részhalmaz, melyre teljesülnek az alábbi tulajdonságok:
(a) a sík bármely tengelypárhuzamos (azaz függőleges vagy vízszintes) egyenese K-t legfeljebb 2 pontban metszi,
(b) H∖K bármely pontja rajta van egy K-beli végpontokkal rendelkező, tengelypárhuzamos szakaszon.
 
1. megoldás. Azt mondjuk, hogy K' a H megengedett részhalmaza, ha K'-nek minden függőleges egyenesen legfeljebb két pontja van (tehát vízszintes egyenesen lehet akár több is), és a K' pontjait összekötő tengelypárhuzamos szakaszok lefedik H minden pontját. Létezik megengedett halmaz: ilyen K'-t alkotnak például H mindazon pontjai, amelyek a saját függőleges egyenesükön legalsók vagy legfelsők, hiszen ekkor már a K' pontjai meghatározta függőleges szakaszok lefedik H minden pontját.
Legyen K egy olyan megengedett halmaz, amelyre a K pontjait összekötő függőleges (esetleg ponttá fajuló) zárt szakaszok által lefedett H-beli pontok száma minimális. Állítjuk, hogy ez a K kielégíti a feladat követelményeit. A K halmaz megengedettsége miatt mindössze azt kell belátnunk, hogy K-nak minden vízszintes egyenesen legfeljebb két pontja van.
Indirekt bizonyítunk. Tegyük fel, hogy K három pontja, mondjuk p, q és r egy vízszintes egyenesre esnek úgy, hogy a q a p és az r között van. Ha a q pontot tartalmazó függőleges egyenesen K-nak nincs más pontja, akkor legyen K'=K∖{q}. Ha van, akkor pontosan egy van (mondjuk s). Legyen q' a qs nyílt félegyenesnek a q végponthoz legközelebbi H-beli pontja (ilyen van, mert s∈K⊆H), és legyen K'=K∖{q}∪{q'}. Mindkét esetben K'⊆H, K'-nek minden függőleges egyenesen legfeljebb két pontja van, és a K' pontjait összekötő tengelypárhuzamos szakaszok lefedik H∖K' minden pontját. Ráadásul a K' pontjait összekötő függőleges (esetleg ponttá fajuló) zárt szakaszok által lefedett H-beli pontok száma kisebb, mint ugyanez a szám a K esetén. Ez nem lehetséges.
A kapott ellentmondás igazolja, hogy a K halmaz a feladatban megfogalmazott mindkét feltételt teljesíti.  □
 

A fenti érvelés bár igazolja a feladat állítását, nem ad jól használható algoritmust egy megfelelő K halmaz megtalálására. Az alábbi megoldás ezzel is szolgál.
 
2. megoldás. A H halmaz mérete szerinti indukcióval bizonyítunk. Világos, hogy ha |H|=1, akkor K=H teljesíti a feladatbeli feltételeket. Tegyük fel, hogy legfeljebb n pontú H halmazra már igazoltuk az állítást, és legyen a H halmaznak n+1 pontja.
Alkossák a K* halmazt a H azon pontjai, amelyek a saját függőleges egyenesükön legalsók vagy legfelsők. Világos, hogy K* teljesíti a feladat (b) feltételét. Ha az (a) feltétel is teljesül K*-ra, akkor készen vagyunk: K=K* megfelelő. Ha azonban az (a) feltétel nem teljesül, akkor ennek az az oka, hogy van K*-nak olyan q pontja, hogy a q vízszintes egyenesén q-tól balra és jobbra is van K*-nak pontja, mondjuk p és r.
Az indukciós feltevés szerint az n pontú H∖{q} halmaznak létezik olyan K részhalmaza, ami minden tengelypárhuzamos egyenesen legfeljebb két pontot tartalmaz, és H∖{q} minden pontját lefedik a K által meghatározott tengelypárhuzamos szakaszok. Állítjuk, hogy ugyanez a K halmaz H-hoz is megfelelő. Ehhez elegendő azt belátnunk, hogy q rajta van egy K-beli végpontokkal rendelkező vízszintes szakaszon. Vizsgáljuk a p pontot! Mivel p egy függőleges egyenes H-beli legalsó vagy legfelső pontja, azért vagy p∈K, vagy p egy K-végpontú vízszintes szakaszon található, tehát q vízszintes egyenesén van p-től balra K-nak pontja. Hasonlóan, ha r∉K, akkor r is csak egy K meghatározta vízszintes szakaszon lehet, így K-nak r-től jobbra is van pontja. Azt kaptuk, hogy q csakugyan egy K végpontú vízszintes szakasz belsejében van, tehát K valóban megfelel a feladat feltételeinek, vagyis az állítás n+1 pontú halmazokra is igaz. Ezzel az indukciós lépést igazoltuk, a bizonyítást befejeztük.  □
 
Megjegyzések. 1. A 2. megoldásból úgy kaphatunk hatékony algoritmust a K halmaz keresésére, hogy első lépésben képezzük a K* halmazt. Ha K* nem alkalmas K-nak a bizonyításbeli q pontja miatt, akkor a H∖{q} halmazra rekurzívan meghívjuk ugyanezt az algoritmust. Így legfeljebb |H|-1 alkalommal képezve a megfelelő K* halmazt, előbb-utóbb egy keresett K-t kapunk. (Az is könnyen látható, hogy nem kell egyenként elhagyni a q pontokat: megtehetjük azt is, hogy H-ból egyszerre hagyjuk el K* összes olyan pontját, ami K*-beli végpontokkal rendelkező vízszintes szakasz belsejében van. Így az algoritmus gyorsabban végetér.)
2. Több hamis bizonyítás érkezett a feladatra. Legtöbbjük módszeréből az is következne, hogy tetszőleges H halmazhoz egyértelműen létezik a keresett K. A példa mutatja, hogy ez koránt sincs így.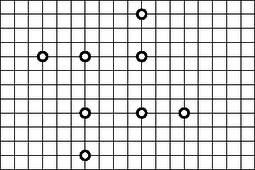
 
 

3. Érdekes tulajdonsága a fenti megoldásokban konstruált K halmaznak, hogy ha egy K' halmaz rendelkezik a feladatbeli (a) és (b) tulajdonságokkal, akkor minden K'-beli végpontokkal rendelkező függőleges szakasz része egy K meghatározta függőleges szakasznak, továbbá minden K meghatározta vízszintes szakasz része egy K'-beli végpontokkal rendelkező vízszintes szakasznak. Más szóval K a ,,legmagasabb'' és egyben ,,legkeskenyebb'' a kívánt tulajdonságú halmazok között. Természetesen ha a 90∘-kal elforgatott ábrán végezzük el a konstrukciót (azaz a függőleges és vízszintes szavakat felcseréljük a bizonyításban), akkor a ,,legalacsonyabb'' és ,,legszélesebb'' megoldást kapjuk meg.
4. A feladat szoros rokonságot mutat Gale és Shapley (sajnos nem eléggé) ismert ,,stabil házassági'' tételével.