Cím:	Megoldásvázlatok a 2007/9. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2008/január, 13 - 18. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Oldjuk meg a valós számok halmazán az alábbi egyenletet: $\begin{array}{c}{\displaystyle \frac{2x^2-10x+9}{x^2-4x-12}=\frac{x^2-x-9}{\left(x-6\right)\left(x+2\right)}\mathrm{.}\text{<span style="font-weight: normal;font-style: normal;">(<span style="font-style: italic;">11 pont</span>)</span>}}\end{array}$   Megoldás. A két nevező egyenlő. A feladat értelmezési tartománya: $x\in \text{R}\backslash \left\{-2;6\right\}$. A számlálóknak is egyenlőnek kell lenni: $2x^2-10x+9=x^2-x-9$. A következő másodfokú egyenletet kapjuk: $\begin{array}{c}{\displaystyle x^2-9x+18=0.}\end{array}$ A gyökök: $x_1=3$, $x_2=6$. A feladat megoldása az $x_1=3$, mert csak ez van benne az értelmezési tartományban. 2. Az $ABC$ háromszög oldalainak hossza $26$, $28$ és $30$. $a)$ Igazoljuk, hogy a háromszög hegyesszögű! $b)$ Mekkora a háromszög leghosszabb magassága? $c)$ Az $ABC$ háromszög síkjával párhuzamos síkban van egy $A\text{'}B\text{'}C\text{'}$ háromszög, amely az $ABC$ háromszöghöz középpontosan hasonló, a hasonlóság aránya $0\mathrm{,}5$. A két párhuzamos sík távolsága $12$. Mennyi az $ABCA\text{'}B\text{'}C\text{'}$ test térfogata?  (12 pont)   Megoldás. $a)$ Számoljuk ki az $ABC$ háromszög leghosszabb oldalával szemközti, legnagyobb $\gamma$ szögét. Írjuk föl a koszinusz-tételt a $\gamma$ szögre: $\begin{array}{c}{\displaystyle {30}^2={26}^2+{28}^2-2\cdot 26\cdot 28\cdot \text{cos}\gamma \mathrm{,}}\end{array}$ amiből $\text{cos}\gamma \approx 0\mathrm{,}3846$. Vagyis a háromszög legnagyobb szöge hegyes ($\gamma \approx 67\mathrm{,}{4}^{\circ })$, így a háromszög hegyesszögű. $b)$ Számoljuk ki az $ABC$ háromszög területét. A Heron-képlet szerint $\begin{array}{c}{\displaystyle T=\sqrt[]{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}\mathrm{,}}\end{array}$ ahol $s$ a háromszög kerületének felét, az $a$, $b$, $c$ pedig a háromszög oldalainak a hosszát jelenti. Vagyis $T=\sqrt[]{42\cdot 12\cdot 14\cdot 16}=336$. A leghosszabb $m_a$ magasság a legrövidebb oldalhoz tartozik. Ezzel felírva a területet: $\begin{array}{c}{\displaystyle 336=\frac{26\cdot m_a}{2}\mathrm{,}\text{amiből}{m}_a=\frac{336}{13}\approx 25\mathrm{,}83.}\end{array}$ $c)$ Az $ABC$ háromszög területe $T=336$. A hozzá hasonló háromszög területe: $t=\frac{1}{4}\cdot 336=84$, mivel a hasonlóság aránya 0,5, és a terület a hasonlóság arányának négyzetével arányos. A kérdéses test egy csonkagúla, írjuk fel a térfogatát: $\begin{array}{c}{\displaystyle V=\frac{m}{3}\left(T+\sqrt[]{Tt}+t\right)=\frac{12}{3}\cdot \left(336+\sqrt[]{336\cdot 84}+84\right)=2352.}\end{array}$ 3. $a)$ Hány olyan négyjegyű szám van, amely osztható $3$-mal és $9$-re végződik? $b)$ Ha egy számtani sorozat első $51$ darab páratlan sorszámú elemének összegéből kivonjuk az első $50$ darab páros sorszámú elemének összegét, különbségként $2007$-et kapunk. Ha ugyanennek a számtani sorozatnak az első $50$ darab páros sorszámú elemének összegéből kivonjuk az első $50$ darab páratlan sorszámú elemének összegét, akkor pedig $2000$ a különbség. Határozzuk meg a sorozat $101$. elemét.  (14 pont)   Megoldás. $a)$ A 9-re végződő négyjegyű szám akkor osztható 3-mal, ha a 9 előtt levő háromjegyű szám osztható 3-mal. 900 háromjegyű szám van, és ezek közül minden harmadik, azaz 300 darab osztható 3-mal. Vagyis 300 darab olyan négyjegyű szám van, amely osztható 3-mal és 9-re végződik. $b)$ Legyen a számtani sorozat első eleme $a$, a differenciája $d$. Az első 51 darab páratlan sorszámú elemének összege: $51a+2550d$. Az első 50 darab páros sorszámú elemének összege: $50a+2500d$. Az első 50 darab páratlan sorszámú elemének összege: $50a+2450d$. A szöveg szerint: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(51a+2550d\right)-\left(50a+2500d\right)=a+50d}& {\displaystyle =\mathrm{2007,}}\hfill \\ \hfill {\displaystyle \text{és}\left(50a+2500d\right)-\left(50a+2450d\right)=50d}& {\displaystyle =2000.}\hfill \end{array}}$ Vagyis $d=40$, $a=7$. A sorozat 101. eleme az $a+100d=7+100\cdot 40=4007$. 4. Mekkora szögben látszik a $PQ$ szakasz az $y=x^2-2x-2$ egyenlettel megadott alakzat $P\left(-1;1\right)$ és $Q\left(2;-2\right)$ pontjában húzott érintők metszéspontjából? Adjuk meg az érintők metszéspontjának koordinátáit.  (14 pont)   Megoldás. Az érintő meredekségét az első derivált adja: 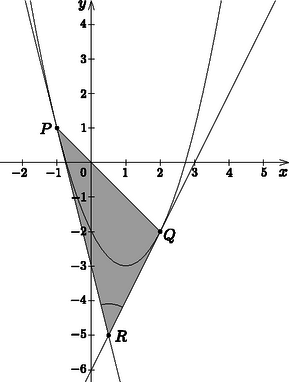$\begin{array}{c}{\displaystyle \left(x^2-2x-2\right)\text{'}=2x-2.}\end{array}$ A $P$ pontra illeszkedő érintő meredeksége $-4$, a $Q$ pontra illeszkedő érintő meredeksége 2. A $P$-re illeszkedő érintő egyenlete: $\begin{array}{c}{\displaystyle e_P:y-1=-4\left(x+1\right)\mathrm{,}}\end{array}$ azaz $y=-4x-3$. A $Q$-ra illeszkedő érintő egyenlete: $\begin{array}{c}{\displaystyle e_Q:y+2=2\left(x-2\right)\mathrm{,}}\end{array}$ azaz $y=2x-6$. Vagyis a két érintő metszéspontja: $R\left(\frac{1}{2};-5\right)$.     A $PQR$ háromszög oldalainak hosszát kiszámítjuk a csúcsok koordinátáiból: $RQ=\sqrt[]{11\mathrm{,}25}$, $RP=\sqrt[]{38\mathrm{,}25}$, $PQ=3\sqrt[]{2}$. Írjuk fel a koszinusz-tételt a kérdéses szögre: $\begin{array}{c}{\displaystyle 18=11\mathrm{,}25+38\mathrm{,}25-2\cdot \sqrt[]{11\mathrm{,}25}\cdot \sqrt[]{38\mathrm{,}25}\cdot \text{cos}\phi \mathrm{,}}\end{array}$ ahonnan $\text{cos}\phi \approx 0\mathrm{,}7593$, vagyis $\phi \approx 40\mathrm{,}{6}^{\circ }$.   II. rész   5. Legyen $P$ az $ABCD$ négyzet $AC$ átlójának az a pontja, amelyre $AP=AB=1$. Az $AC$ átlóra a $P$ pontban állított merőleges egyenes a $BC$ oldalt a $Q$ pontban metszi. Az $ABCD$ sík $P$ pontjában a síkra állított merőleges egyenesre mérjük fel a $PE=1$ távolságot. $a)$ Igazoljuk, hogy az $ABQP$ négyszög deltoid. $b)$ A deltoid területe hányadrésze a négyzet területének? $c)$ Számítsuk ki az $ABCDE$ gúla oldallapjainak az alaplap síkjával bezárt hajlásszögét.  (16 pont)   Megoldás. $a)$ A feltétel szerint $AP=AB=1$ és $AC=\sqrt[]{2}$, azért $PC=\sqrt[]{2}-1$. A $CPQ$ derékszögű háromszögben a $C$-nél ${45}^{\circ }$ van, ezért $PQ=PC=\sqrt[]{2}-1$. A $CPQ$ derékszögű háromszög átfogójának hossza: $CQ=\sqrt[]{2}\left(\sqrt[]{2}-1\right)=2-\sqrt[]{2}$. Ebből következik, hogy $BQ=CB-CQ=1-\left(2-\sqrt[]{2}\right)=\sqrt[]{2}-1$. Vagyis $AP=AB$, valamint $BQ=PQ$, így az $ABQP$ négyszög valóban deltoid. 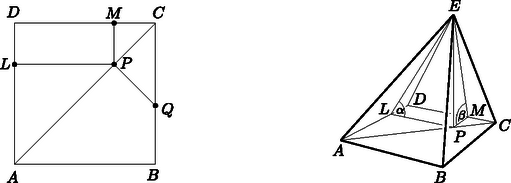    $b)$ Az $ABCD$ négyzet területe 1. Mivel az $ABQP$ négyszög derékszögű deltoid, azért területe: $t=AB\cdot BQ=1\cdot \left(\sqrt[]{2}-1\right)\approx 0\mathrm{,}41$. Ennyied része a deltoid területe a négyzet területének. $c)$ Két-két oldallap hajlásszöge megegyezik, így két szöget kell kiszámítanunk. A $P$ pontból az $AD$ élre állított merőleges talppontja legyen $L$, a $DC$ élre állított merőlegesé pedig $M$. Az $APL$ és a $PCM$ egyenlő szárú derékszögű háromszögek felhasználásával: $LP=\frac{1}{\sqrt[]{2}}$, $MP=\frac{\sqrt[]{2}-1}{\sqrt[]{2}}$. A keresett $\alpha$, illetve $\beta$ szögek az $LPE$ és az $MPE$ derékszögű háromszögekből határozhatók meg: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \text{tg}\alpha =\frac{1}{\frac{1}{\sqrt[]{2}}}=\sqrt[]{2}\mathrm{,}}& {\displaystyle \text{vagyis}}\hfill & {\displaystyle \alpha \approx 54\mathrm{,}{74}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{és}\text{tg}\beta =\frac{1}{\frac{\sqrt[]{2}-1}{\sqrt[]{2}}}=\frac{\sqrt[]{2}}{\sqrt[]{2}-1}\mathrm{,}}& {\displaystyle \text{vagyis}}\hfill & {\displaystyle \beta \approx 73\mathrm{,}{68}^{\circ }\mathrm{.}}\hfill \end{array}}$ 6. A ${10}^n+{14}^n+{15}^n+{21}^n$ kifejezésben az $n$  $3$-mal osztható pozitív páratlan1 egész számot jelöl. $a)$ Igazoljuk, hogy a négytagú összeg minden ilyen $n$ esetén osztható lesz $1260$-nal. $b)$ A négytagú összeg két tagját véletlenszerűen kiválasztjuk. Mekkora valószínűséggel lesz a két tag összege hárommal osztható?  (16 pont)   Megoldás. $a)$ Alakítsuk át a négytagú kifejezést: $\begin{array}{c}{\displaystyle {10}^n+{14}^n+{15}^n+{21}^n=2^n\cdot 5^n+2^n\cdot 7^n+3^n\cdot 5^n+3^n\cdot 7^n=\left(2^n+3^n\right)\left(5^n+7^n\right)\mathrm{.}}\end{array}$ Legyen $n=3k$, ahol $k$ páratlan pozitív egész számot jelöl. Ekkor $\begin{array}{c}{\displaystyle \left(2^n+3^n\right)\left(5^n+7^n\right)=\left(2^{3k}+3^{3k}\right)\left(5^{3k}+7^{3k}\right)=\left(8^k+{27}^k\right)\left({125}^k+{343}^k\right)\mathrm{.}}\end{array}$ Mivel a kitevők páratlan számok, azért $35\mid 8^k+{27}^k$ és $468\mid {125}^k+{343}^k$. A 468 osztható 36-tal, és $\left(35;36\right)=1$, ezért a kifejezés osztható $35\cdot 36=1260$-nal. $b)$ A négytagú összeg két tagját hatféleképpen választhatjuk ki. Mivel a kitevők páratlan számok, azért az összeg osztható lesz az alapok összegével. Az alapok összege a következő hat érték közül kerülhet ki: 24, 25, 31, 29, 35, 36. Ezek közül két szám osztható hárommal, vagyis két esetben biztosan 3-mal osztható az összeg. A további négy esetben nem kaphatunk 3-mal osztható számot, mert a kéttagú összeg egyik tagja osztható 3-mal, a másik pedig nem. Így a keresett valószínűség $\frac{1}{3}$. 7. Igazoljuk, hogy a valós számok halmazán értelmezett $f\left(x\right)=8x^3-6x-1$ hozzárendeléssel megadott függvénynek három különböző zérushelye van és ezek közül a legnagyobb: $x_1=\text{cos}\frac{\pi }{9}$.  (16 pont)   Megoldás. Tudjuk, hogy $f\left(x\right)$ mindenütt folytonos függvény. Mivel az 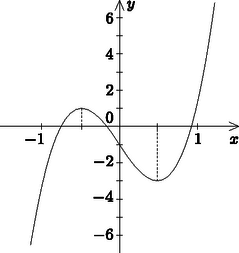$\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=24x^2-6}\end{array}$ függvény zérushelyei a $-\frac{1}{2}$ és az $\frac{1}{2}$, azért itt lehet az eredeti függvénynek lokális szélsőértéke. Ezeken a helyeken az első derivált előjelet vált (pozitívból negatívba, illetve negatívból pozitívba megy át), így az első helyen lokális maximuma, a második helyen lokális minimuma van a függvénynek. Számolással kapjuk, hogy $f\left(-0\mathrm{,}5\right)=1$ és $f\left(0\mathrm{,}5\right)=-3$. Vagyis a $\left]-\frac{1}{2};\frac{1}{2}\right]$ intervallumon van zérushelye a függvénynek. ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↗</mo></math>}}\hfill & \hfill {\displaystyle \text{maximum}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↘</mo></math>}}\hfill & \hfill {\displaystyle \text{minimum}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↗</mo></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mo stretchy="false">'</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill \\ \hline\end{array}}$     Mivel $\underset{x\to \infty }{\overset{}{\text{lim}}}\left(8x^3-6x-1\right)=\infty$, azért az $\left]\frac{1}{2};\infty \right[$ intervallumon is van zérushelye a függvénynek. Mivel $\underset{x\to -\infty }{\overset{}{\text{lim}}}\left(8x^3-6x-1\right)=-\infty$, azért a $\left]-\infty ;-\frac{1}{2}\right]$ intervallumon is van zérushelye a függvénynek. Azaz van három különböző zérushelye. Mivel $f\left(0\right)=-1$, azért a középső zérushelyről az is megállapítható, hogy a $\left]-\frac{1}{2};0\right]$ intervallumon található. Ez azt jelenti, hogy két negatív és egy pozitív zérushellyel rendelkezik a függvény. Tudjuk, hogy $\text{cos}\frac{\pi }{9}>0$, ezért ha az $x_1=\text{cos}\frac{\pi }{9}$ valóban zérushelye a függvénynek, akkor az a három zérushely közül csakis a legnagyobb lehet. A $\frac{\pi }{9}$ háromszorosa $\frac{\pi }{3}$, ami nevezetes szög. Tudjuk, hogy $\text{cos}\frac{\pi }{3}=\frac{1}{2}$. Alkalmazzuk a $\text{cos}3\alpha =4\text{cos}{}^3\alpha -3\text{cos}\alpha$ összefüggést: $\begin{array}{c}{\displaystyle \text{cos}\frac{\pi }{3}=4\text{cos}{}^3\frac{\pi }{9}-3\text{cos}\frac{\pi }{9}\mathrm{.}}\end{array}$ Ezt 2-vel szorozva és rendezve kapjuk: $\begin{array}{c}{\displaystyle 8\text{cos}{}^3\frac{\pi }{9}-6\text{cos}\frac{\pi }{9}-1=0.}\end{array}$ Ez pontosan azt jelenti, hogy az $f\left(x\right)=8x^3-6x-1$ hozzárendelésű függvénynek az $x_1=\text{cos}\frac{\pi }{9}$ a zérushelye. 8. $a)$ Egy szabályos sokszöget két átlójával négy síkidomra vágtunk: négyszögre, ötszögre, hatszögre és nyolcszögre. Hány oldala van a szabályos sokszögnek? $b)$ Egy szabályos tizenötszög csúcsait pirosra, a belsejében pedig néhány pontot zöldre színeztünk. Az így kapott színes pontokat minden lehetséges módon páronként összekötöttük egy-egy szakasszal. Azon szakaszok száma, amelyeknek a végpontjai azonos színűek megegyezik azon szakaszok számával, amelyeknek a két végpontja nem azonos színű. Hány darab zöld pontot vettünk fel a sokszög belsejében?  (16 pont)   Megoldás. $a)$ A feladatban szereplő két átló metszi egymást. Az átlók egy-egy darabja oldala lesz a keletkezett sokszögeknek. Mind a négy sokszögben két-két oldal az átlók egy-egy darabja lesz. Ezért a négyszögnek kettő, az ötszögnek három, a hatszögnek négy, a nyolcszögnek pedig hat olyan oldala van, amely az eredeti sokszögnek is oldala. Az eredeti sokszög minden oldala szerepel valamelyik keletkező sokszög oldalaként. Ezért az eredeti sokszögnek $2+3+4+6$, azaz 15 oldala van.     $b)$ Legyen a zöld pontok száma $n$. A piros végű szakaszok száma $\left(\genfrac{}{}{0ex}{}{15}{2}\right)$, a zöld végű szakaszok száma $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$. Azon szakaszok száma, amelyeknek az egyik vége piros, a másik pedig zöld, $15n$. Felírhatjuk a következő egyenletet: $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{n}{2}\right)+\left(\genfrac{}{}{0ex}{}{15}{2}\right)=15n\mathrm{,}\text{azaz}\frac{n\left(n-1\right)}{2}+\frac{15\cdot 14}{2}=15n\mathrm{.}}\end{array}$ Rendezzük az egyenletet: $n^2-31n+210=0$. A két gyök: $n_1=10$, $n_2=21$. Vagyis a zöld pontok száma 10 vagy 21. 9. Oldjuk meg a következő egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle \sqrt[]{{\left(7+4\sqrt[]{3}\right)}^x}+\sqrt[]{{\left(7-4\sqrt[]{3}\right)}^x}=\frac{5}{2}\mathrm{.}}\end{array}$ (16 pont)   Megoldás. Alakítsuk át az egyenletet, felhasználva, hogy ${\left(2+\sqrt[]{3}\right)}^2=\left(7+4\sqrt[]{3}\right)$ és hasonlóképpen ${\left(2-\sqrt[]{3}\right)}^2=\left(7-4\sqrt[]{3}\right)$: $\begin{array}{c}{\displaystyle \sqrt[]{{\left(2+\sqrt[]{3}\right)}^{2x}}+\sqrt[]{{\left(2-\sqrt[]{3}\right)}^{2x}}=\frac{5}{2}\mathrm{,}\text{innen}{\left(2+\sqrt[]{3}\right)}^x+{\left(2-\sqrt[]{3}\right)}^x=\frac{5}{2}\mathrm{.}}\end{array}$ Legyen ${\left(2+\sqrt[]{3}\right)}^x=a$, ekkor ${\left(2-\sqrt[]{3}\right)}^x=\frac{1}{a}$. Megoldjuk az $a+\frac{1}{a}=\frac{5}{2}$ egyenletet, amit $2a$-val szorozva és rendezve kapjuk, hogy: $\begin{array}{c}{\displaystyle 2a^2-5a+2=0.}\end{array}$ A gyökök: $a_1=2$, $a_2=\frac{1}{2}$. A ${\left(2+\sqrt[]{3}\right)}^x=2$ egyenletből kapjuk, hogy $\begin{array}{c}{\displaystyle x_1=\frac{\text{lg}2}{\text{lg}\left(2+\sqrt[]{3}\right)}\approx 0\mathrm{,}5263.}\end{array}$ A ${\left(2+\sqrt[]{3}\right)}^x=\frac{1}{2}$ egyenletből kapjuk, hogy $\begin{array}{c}{\displaystyle x_2=\frac{\text{log}\frac{1}{2}}{\text{lg}\left(2+\sqrt[]{3}\right)}=-\frac{\text{lg}2}{\text{lg}\left(2+\sqrt[]{3}\right)}\approx -0\mathrm{,}5263.}\end{array}$ 1A ,,páratlan'' szó múlt havi feladatsorunkban kimaradt, ettől a feladat pontatlanná vált. A hibáért elnézést kérünk.