A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.
A 38. Nemzetközi Fizikai Diákolimpia elméleti feladatai
1. feladat. Kettőscsillagok
A kettőscsillag rendszerek két csillagból állnak, melyek közös tömegközéppontjuk körül keringenek. Galaxisunkban a csillagoknak csaknem a fele kettőscsillag rendszert alkot. A Földről nem könnyű megállapítani a legtöbb ilyen csillag rendszer kettős természetét, mert a két csillag közötti távolság sokkal kisebb, mint a tőlünk mérhető távolság, így a távcsövekkel csak egyetlen fénylő pontot látunk. Ezért inkább fotometriát (fényességmérést) és spektroszkópiát (színképelemzést) használunk, ilyen módon észlelhetjük az adott csillag intenzitásának vagy színképének a változásait, melyek segítségével eldönthetjük, hogy az adott rendszer kettős vagy sem.
Kettőscsillagok fényességmérése. Ha pontosan a két csillag mozgásának síkjában vagyunk, akkor az egyik csillag időről időre elhalad a másik előtt, és ezért az egész rendszer fényének intenzitása időben változni fog a mi megfigyelési helyünkön. Az ilyen kettős rendszereket ekliptikus kettős rendszereknek nevezzük.
1. Tegyük fel, hogy a két csillag mindegyike körpályán mozog a közös tömegközéppontjuk körül állandó szögsebességgel, és mi pontosan a kettős rendszer mozgásának síkjában vagyunk. Ugyancsak tegyük fel, hogy a két csillag felületi hőmérséklete és (), valamint sugaraik és ().
A fény Földről mérhető teljes intenzitását az idő függvényében az 1. ábra mutatja.
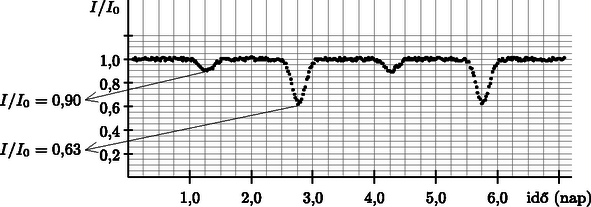 1. ábra. A kettőscsillag rendszerből érkező fény relatív intenzitása az idő függvényében. A függőleges tengely skálázása értékhez viszonyított. Az idő napokban van mérve
A gondosan elvégzett mérések szerint a csillagokból érkező fény intenzitásminimumai a mindkét csillagból jövő fény maximális intenzitásának () 90, illetve 63 százalékával egyenlők. Az 1. ábrán a függőleges tengely az intenzitás arányt mutatja, míg a vízszintes tengelyen az idő van feltüntetve nap egységekben.
1.1. (0,8 pont) Olvasd le a mozgás periódusidejét!
Válaszodat add meg másodperc egységben két értékes jegy pontossággal!
Mekkora a rendszer szögsebessége radián/másodperc (rad/s) egységben?
Jó közelítéssel igaz, hogy egy csillagról érkező sugárzás olyan abszolút feketetest sugárzásnak felel meg, mint ami egy akkora sugarú lapos korongról érkezne, mint a csillag sugara. Ezért a csillagról érkező intenzitás -nel arányos, ahol a korong területe és a csillag felszínének hőmérséklete.
1.2. (1,6 pont) Az 1. ábrán található grafikon segítségével határozd meg a és arányokat.
Kettős rendszerek színképelemzése. Ebben a részben a kettőscsillag rendszer kísérleti színkép adatai alapján kiszámítjuk a kettőscsillag néhány csillagászati jellemzőjét.
Az atomok sugárzást nyelnek el vagy bocsátanak ki bizonyos jellegzetes hullámhosszakon. Következésképpen egy csillag észlelhető színképe elnyelési (abszorpciós) vonalakat tartalmaz a csillag felszíni légkörében található atomoknak megfelelően.
A nátrium jellegzetes sárga színképvonalának ( vonal) hullámhossza: 5895,9 (). Vizsgáljuk meg az előző részben szereplő kettős rendszer esetén az atomi nátriumnak ezt a hullámhosszát. A kettőscsillagról érkező fény színképe Doppler-eltolódást szenved, mert a csillagok hozzánk képest mozognak. A két csillag sebessége különböző. Ennek megfelelően a két csillag elnyelési hullámhossza különböző mértékben tolódik el. Igen pontos hullámhossz-mérésekre van szükségünk ahhoz, hogy a Doppler-eltolódást észlelhessük, mert a csillagok sebessége sokkal kisebb a fénysebességnél. A kettős rendszer tömegközéppontjának hozzánk képesti sebessége ebben a feladatban sokkal kisebb, mint az egyes csillagok pályamenti sebessége. Ezért az összes Doppler-eltolódást kizárólag a csillagok pályamenti sebességével hozhatjuk kapcsolatba. Az 1. táblázat az általunk vizsgált kettős rendszer csillagjainak mért színképét mutatja.
1. táblázat: A kettőscsillag rendszer elnyelési színképe a nátrium vonalának esetében
(Megjegyzés: Nem szükséges grafikont készíteni ennek a táblázatnak az adataiból.)
2. Használd az 1. táblázatot!
2.1. (1,8 pont) Jelölje az egyes csillagok pályamenti sebességét és ! Határozd meg és értékét!
A fény sebessége: . Hanyagold el a relativisztikus hatásokat!
2.2. (0,7 pont) Határozd meg a csillagok tömegarányát !
2.3. (0,8 pont) Jelölje és az egyes csillagok távolságát a tömegközéppontjuktól! Határozd meg és értékét!
2.4. (0,2 pont) Jelölje a csillagok közötti távolságot! Határozd meg értékét!
3. A csillagok között ható egyetlen erő a gravitációs erő.
3.1. (1,2 pont) Határozd meg az egyes csillagok tömegét egy értékes jegy pontossággal!
Az univerzális gravitációs állandó .
A csillagok általános jellemzői
4. A legtöbb csillagban ugyanolyan módon történik az energiatermelés. Ezért lehetséges egy empirikus (megfigyelésen alapuló) összefüggést felállítani a csillagok tömege és az úgynevezett luminozitása (a csillag által kisugárzott összes teljesítmény) között. Ezt az összefüggést ilyen alakban is megadhatjuk: , ahol a Nap tömege és a Nap luminozitása. A 2. ábra ezt az összefüggést mutatja log‐log diagram alakjában.
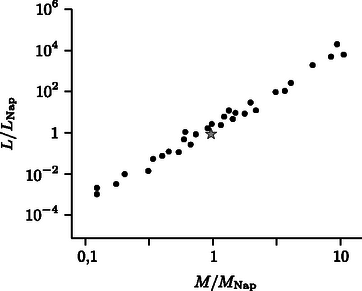 2. ábra. Egy csillag luminozitása a tömegének függvényében hatványfüggvény szerint változik. A grafikon log‐log diagram. A csillaggal jelölt csillag a mi Napunkat mutatja, melynek tömege és luminozitása
4.1. (0,6 pont) Határozd meg értékét 1 értékes jegy pontossággal!
4.2. (0,6 pont) Jelölje és a kettős rendszer csillagainak luminozitását az előzőekben tanulmányozott kettőscsillag esetén! Határozd meg és értékét!
4.3. (0,9 pont) Add meg fényév egységekben, hogy mekkora távolságra van tőlünk a kettőscsillag!
A távolság meghatározásakor használd az 1. ábrán található adatokat! Egy fényév az a távolság, amit a fény egy év alatt tesz meg.
4.4. (0,4 pont) Mekkora a két csillag közötti maximális látószög a földi észlelési pontból nézve?
4.5. (0,4 pont) Legalább mekkora legyen egy optikai távcső apertúra- (nyílás-) mérete, hogy megfelelő felbontóképességet biztosítson a két csillag külön-külön észleléséhez?
2. feladat. Légzsák
Ebben a feladatban azoknak a gyorsulásmérőknek az egyszerűsített modelljével foglalkozunk, amelyek ütközéskor az autók légzsákját hozzák működésbe. Egy olyan elektromechanikai rendszert szeretnénk építeni, amelyben a gyorsulás egy meghatározott értékénél valamelyik elektromos mennyiség (például a feszültség az áramkör egy adott pontján) elér egy küszöbértéket, és ennek hatására a légzsák működésbe lép.
Megjegyzés: Ebben a feladatban hanyagold el a gravitációt!
1. Tekintsünk egy kondenzátort, amely két párhuzamos lemezből áll (3. ábra). A kondenzátor mindkét lemeze területű, a lemezek közti távolság . A lemezek közti távolság sokkal kisebb, mint a lemezek méretei. Az egyik lemezt egy rugóállandójú (direkciós erejű) rugó egy falhoz kapcsolja, a másik lemez rögzített. Ha a lemezek közti távolság , akkor a rugó nincsen sem megnyújtva, sem összenyomva. Más szavakkal: ekkor semmilyen erő nem lép fel a rugóban. Tegyük fel, hogy a lemezek közt a levegő permittivitása megegyezik a vákuuméval (). A kondenzátor kapacitása a lemezek ekkora távolságánál: . A lemezekre és töltést juttatunk, és hagyjuk, hogy a rendszer mechanikailag egyensúlyba kerüljön.
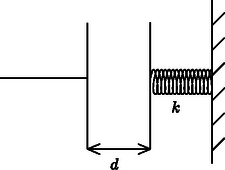 3. ábra
1.1. (0,8 pont) Számítsd ki a lemezek által egymásra kifejtett elektromos erőt!
1.2. (0,6 pont) A rugóhoz rögzített lemez elmozdulását jelölje . Határozd meg értékét!
1.3. (0,4 pont) Mekkora ebben az állapotban a kondenzátor lemezei közti potenciálkülönbség , , , függvényében kifejezve?
1.4. (0,3 pont) Legyen a kondenzátor kapacitása (amit a töltés és a potenciálkülönbség hányadosaként definiálunk). Határozd meg a hányadost , , és függvényében!
1.5. (0,6 pont) Mekkora a rendszerben tárolt teljes energia , , és függvényében kifejezve?
A 4. ábra egy tömegű testet mutat, amelyet egy elhanyagolható tömegű vezető lemezhez és két egyforma, rugóállandójú rugóhoz rögzítettünk. A vezető lemez előre-hátra tud mozogni két rögzített vezető lemez között. A lemezek egyformák, területük . A három lemez így két kondenzátort képez. A rögzített lemezek a 4. ábrán látható módon és feszültségre vannak kapcsolva, a középső lemez pedig egy kétállású kapcsolón keresztül le van földelve. A középső lemezre kötött vezeték nem akadályozza a lemez mozgását, és a lemezek mindvégig párhuzamosak. Ha az egész rendszer nem gyorsul, akkor mindkét rögzített lemez távolságra van a mozgó lemeztől (ez a távolság sokkal kisebb, mint a lemezek méretei). A mozgó lemez vastagsága elhanyagolható.
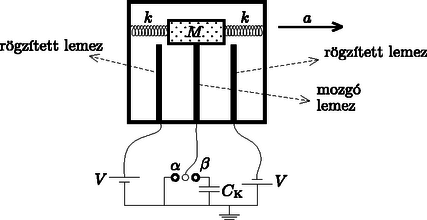 4. ábra
A kapcsoló az és állapotokban lehet. Tegyük fel, hogy a rendszer az autóval együtt gyorsul, és gyorsulása állandó. Tegyük föl azt is, hogy az állandó gyorsulás mellett a rugó nem rezeg, és az összetett kondenzátorrendszer minden eleme egyensúlyi állapotban van, azaz az egyes elemek egymáshoz (és így az autóhoz képest is) nyugalomban vannak.
A gyorsulás hatására a mozgó lemez távolsággal elmozdul eredeti helyéről, a két rögzített lemez közötti felezőponttól.
2. Tekintsük először azt az esetet, amikor a kapcsoló az állásban van, azaz a mozgó lemez le van földelve!
2.1. (0,4 pont) Határozd meg ebben az esetben mindkét kondenzátor töltését függvényében!
2.2. (0,4 pont) Határozd meg a mozgó lemezre ható eredő elektromos erőt függvényében!
2.3. (0,2 pont) Tegyük fel, hogy és az rendű tagok elhanyagolhatók a rendű tagok mellett. Egyszerűsítsd a 2.2. részben kapott képletet!
2.4. (0,7 pont) Írd fel a mozgó lemezre ható teljes erőt (az elektromos és rugóerők eredőjét) alakban, és határozd meg a -et megadó képletet!
2.5. (0,4 pont) Fejezd ki az állandó gyorsulást függvényében!
3. Most tekintsük azt az esetet, amikor a kapcsoló a állásban van, azaz a mozgó lemez egy kondenzátoron keresztül van leföldelve. A kondenzátor kapacitása , és kezdetben nincs rajta töltés. A mozgó lemez távolságra tér ki a középponti helyzetéből.
3.1. (1,5 pont) Határozd meg a kondenzátoron eső elektromos feszültséget függvényében!
3.2. (0,2 pont) Megint feltételezzük, hogy , és az nagyságrendű tagok elhanyagolhatók a nagyságrendű tagok mellett. Egyszerűsítsd a 3.1. kérdésre kapott képletet!
4. Szeretnénk a feladatban szereplő paramétereket úgy beállítani, hogy normál fékezésnél a légzsák még ne jöjjön működésbe, de az autó ütközésekor elég gyorsan kinyíljon, és megvédje a vezető fejét a kormánnyal vagy a szélvédővel való ütközéstől. Ahogy a 2. részben láttad, a mozgó lemezre ható elektromos és rugóerő eredője egy effektív rugóállandójú rugóval vehető figyelembe. Az egész összetett kondenzátorrendszer olyan, mint egy tömegből és egy rugóállandójú rugóból álló egyszerű rendszer, amely állandó gyorsulással gyorsul (ami ebben a feladatban megegyezik az autó gyorsulásával).
Megjegyzés: Ebben a részben az a feltevés, hogy a tömeg és a rugó egyensúlyban van az állandó gyorsulás hatására, és így nem mozog az autóhoz viszonyítva, már nem érvényes!
Hanyagold el a súrlódást, és használd a következő numerikus értékeket: , , , , , .
4.1. (0,6 pont) Ezeket az adatokat használva határozd meg a 2.3. részben kapott elektromos erő és a rugóerő hányadosát, és mutasd meg, hogy az elektromos erő elhanyagolható a rugóerő mellett!
Abban az esetben, amikor a kapcsoló a állásban van, nem számítjuk ki az elektromos erőt, de az előzőhöz nagyon hasonlóan ekkor is meg lehetne mutatni, hogy az elektromos erők elhanyagolhatók a rugóerők mellett.
4.2. (0,6 pont) Mekkora a mozgó lemez maximális elmozdulása, ha az állandó sebességgel haladó autó hirtelen konstans gyorsulással fékezni kezd? Paraméteres választ adjál!
Tegyük fel, hogy a kapcsoló a állásban van, és a rendszer úgy van megtervezve, hogy ha a kondenzátoron eső feszültség eléri a értéket, a légzsák aktiválódik. Azt szeretnénk, hogy a légzsák ne lépjen működésbe, ha az autó normálisan fékez, azaz gyorsulása kisebb a nehézségi gyorsulásnál (), de azonnal lépjen működésbe, ha a gyorsulás ennél nagyobb.
4.3. (0,6 pont) Mekkora legyen ehhez értéke?
Meg szeretnénk határozni, hogy a légzsák elég gyorsan működésbe lép-e, és meg tudja-e védeni a vezető fejét a kormánnyal vagy a szélvédővel való ütközéstől. Tegyük fel, hogy egy ütközés hatására az autó lassulással lassul, de a vezető feje továbbra is állandó sebességgel mozog.
4.4. (0,8 pont) Becsüld meg a vezető feje és a kormány közötti távolságot, és a becslés alapján határozd meg azt a időt, amely addig telik el, hogy a vezető feje a kormánynak ütközik!
4.5. (0,9 pont) Határozd meg a légzsák aktiválódásáig eltelő időt, és hasonlítsd össze -gyel! Időben működésbe lépett a légzsák? Tételezd fel, hogy a légzsák az aktiválás hatására azonnal kinyílik.
3. feladat. Hawking-sugárzás
Bárhol is találkozunk a fizikában egy egyenlőséggel, az egyenlet mindkét oldala ugyanolyan típusú, azaz ugyanolyan dimenziójú. Például nem lehetséges, hogy az egyenlet jobb oldala hosszúságnak felel meg, míg a bal oldalon álló mennyiség idő intervallumnak. Ezt a tényt felhasználva időnként (számfaktoroktól eltekintve) fizikai összefüggéseket állapíthatunk meg a probléma analitikus megoldása nélkül. Például, ha azt kérdezzük, hogy a magasságból elengedett test mennyi idő alatt esik le az állandónak tekinthető gravitációs gyorsulás hatására, akkor úgy érvelhetünk, hogy egy idő intervallumot reprezentáló mennyiséget kell felépítenünk és segítségével, és ennek egyetlen módja ez: . Vegyük észre, hogy ez a megoldás tartalmaz egy dimenzió nélküli, nem meghatározott együtthatót, melyet ezzel a módszerrel nem lehet megkapni. Ez az együttható egy ilyen szám lehet: 1, , , vagy bármilyen más valós szám. Fizikai összefüggéseknek ilyen módszerrel történő levezetését dimenzióanalízisnek nevezzük. Dimenzióanalíziskor a dimenzió nélküli együtthatók nem fontosak, és ezért nem szükséges leírni ezeket. Szerencsére a legtöbb fizikai probléma esetén ezek az együtthatók nagyságrendileg 1 körüli számok, és elhagyásuk nem változtatja meg a fizikai mennyiségek számértékének nagyságrendjét. Ennek megfelelően a fenti probléma esetén a dimenzió-analízis módszerével ezt az eredményt kapjuk: .
Általánosságban egy fizikai mennyiség dimenziója felírható négy alapmennyiség dimenziójával: (tömeg), (hosszúság), (idő), és (hőmérséklet). Egy tetszőleges mennyiség dimenzióját így jelöljük: . Példaként megmutatjuk, hogy a sebesség, az mozgási (kinetikus) energia és a hőkapacitás dimenziója így írható fel: , , .
Alapvető állandók és a dimenzióanalízis kapcsolata
1.1. (0,8 pont) Határozd meg az alapvető állandók, azaz a Planck-állandó, a fénysebesség, a egyetemes gravitációs állandó és a Boltzmann-állandó dimenzióját a hosszúság, a tömeg, az idő és a hőmérséklet dimenziója segítségével!
A Stefan‐Boltzmann-törvény szerint a feketetest által kisugárzott intenzitás (vagyis az egységnyi felület által egységnyi idő alatt kisugárzott energia) így adható meg: , ahol a Stefan‐Boltzmann-állandó és a feketetest abszolút hőmérséklete.
1.2. (0,5 pont) Határozd meg a Stefan‐Boltzmann-álladó dimenzióját a hosszúság, a tömeg, az idő és a hőmérséklet dimenziója segítségével!
A Stefan‐Boltzmann-állandó nem alapvető állandó, és így felírható az alapvető állandók segítségével, azaz ilyen módon: . Ebben az összefüggésben egy 1 nagyságrendű dimenzió nélküli paraméter. Amint ezt az előzőekben említettük, pontos értéke a mi szempontunkból érdektelen, ezért egyszerűen vegyük 1-nek.
1.3. (1,0 pont) Határozd meg , , és értékét dimenzióanalízissel!
A fekete lyukak fizikája. Ebben a részben dimenzióanalízis segítségével megpróbáljuk meghatározni a fekete lyukak néhány tulajdonságát. Egy bizonyos fizikai elméletnek megfelelően, amit ``no hair'' (,,haja nincs'') elméletnek hívunk, a fekete lyukak összes jellemzője, amelyekkel ebben a feladatban foglalkozunk, kizárólag csak a fekete lyukak tömegétől függ. Egy fekete lyuk egyik jellemzője az eseményhorizontjának a területe. Durván azt mondhatjuk, hogy az eseményhorizont a fekete lyuk határa. Ezen a határon belül a gravitáció olyan erős, hogy az ezzel határolt tartományt még a fény sem képes elhagyni.
Szeretnénk kapcsolatot találni egy fekete lyuk tömege és az eseményhorizont területe között. Ez a terület a fekete lyuk tömegétől, a fénysebességtől és az egyetemes gravitációs állandótól függ. Az 1.3 alkérdés mintájára ezt írhatjuk fel: .
2.1. (0,8 pont) Dimenzióanalízis segítségével határozd meg , , és értékét!
A 2.1. alkérdés eredménye világosan megmutatja, hogy egy fekete lyuk eseményhorizontjának a területe a lyuk tömegével növekszik. Klasszikus leírás szerint semmi sem jön ki a fekete lyukból, és ezért akármilyen fizikai folyamat is történik, az eseményhorizont területe csak növekedhet. A termodinamika második főtételével analógiába állítva ezt, Jacob Bekenstein azt javasolta, hogy érdemes bevezetni a fekete lyukak entrópiáját, amit tekintsünk arányosnak a lyuk eseményhorizontjának területével, azaz . Más érvelések megerősítették ezt a felvetést.
2.2. (0,2 pont) Az entrópia termodinamikai definíciója () alapján határozd meg az entrópia dimenzióját!
a hőközlés mértéke és a rendszer abszolút hőmérséklete.
2.3. (1,1 pont) Ugyanúgy, mint az 1.3. alkérdésben, fejezd ki a dimenzióval rendelkező állandót mint az alapvető fizikai állandók (, , , és ) függvényét!
A továbbiakban ne használd a dimenzióanalízis módszerét, azonban felhasználhatod az eddigi alkérdésekre kapott eredményeidet!
3. Hawking-sugárzás. Fél-kvantummechanikai tárgyalással Stephen Hawking úgy érvelt, hogy ‐ a klasszikus tárgyalással ellentétben ‐ a fekete lyukak a feketetest-sugárzáshoz hasonlóan sugárzást bocsáthatnak ki. Úgy sugároznak, mint egy adott hőmérsékletű feketetest, ezt a hőmérsékletet Hawking-hőmérsékletnek nevezzük.
3.1. (0,8 pont) Az összefüggést felhasználva, ami megadja egy fekete lyuk energiáját a tömegével kifejezve, továbbá a termodinamika törvényei alapján, fejezd ki egy fekete lyuk Hawking-hőmérsékletét tömegének és az alapvető fizikai állandóknak a segítségével! Tételezd fel, hogy a fekete lyuk nem végez munkát a környezetén!
3.2. (0,7 pont) Egy környezetétől elszigetelt fekete lyuk a Hawking-sugárzás következtében változtatja a tömegét. A Stefan‐Boltzmann-törvény felhasználásával határozd meg, hogyan függ a fekete lyuk tömegének időbeli változási sebessége (deriváltja) a Hawking-hőmérséklettől, és fejezd ki ezt a deriváltat a fekete lyuk tömege, valamint az alapvető fizikai állandók segítségével!
3.3. (1,1 pont) Határozd meg azt a időt, ami ahhoz szükséges, hogy egy környezetétől teljesen elszigetelt tömegű fekete lyuk teljesen ,,elpárologjon'', azaz teljesen elveszítse tömegét!
A termodinamika nézőpontjából a fekete lyukak különleges viselkedésekre képesek. Például egy fekete lyuk hőkapacitása negatív.
3.4. (0,6 pont) Határozd meg egy tömegű fekete lyuk hőkapacitását!
4. A fekete lyukak és a kozmikus háttérsugárzás. Tekintsünk egy olyan fekete lyukat, ami ki van téve a kozmikus háttérsugárzásnak. A kozmikus háttérsugárzás egy olyan hőmérsékletű feketetest sugárzás, ami kitölti az egész világmindenséget. Ezért egy teljes felületű test egységnyi idő alatt energiát kap. Ennek megfelelően egy fekete lyuk egyrészt energiát veszít a Hawking-sugárzás következtében, másrészt energiát nyer a kozmikus háttérsugárzásból.
4.1. (0,8 pont) Határozd meg a fekete lyuk tömegének az időbeli változási sebességét a fekete lyuk tömege, a kozmikus háttérsugárzás hőmérséklete és az alapvető fizikai állandók segítségével!
4.2. (0,4 pont) Bizonyos tömeg esetén ez a derivált eltűnik. Határozd meg ezt az tömeget, és fejezd ki és az alapvető fizikai állandók segítségével!
4.3. (0,2 pont) Használd fel a 4.2. alkérdésre adott válaszodat, fejezd ki belőle értékét, és helyettesítsd be a 4.1. részben kapott képletbe. Határozd meg a fekete lyuk tömegének időbeli változási sebességét , és az alapvető fizikai állandók segítségével!
4.4. (0,4 pont) Határozd meg egy fekete lyuk Hawking-hőmérsékletét, amikor a lyuk termikus egyensúlyban van a kozmikus háttérsugárzással!
4.5. (0,6 pont) Ez az egyensúly stabil vagy instabil? Miért? (Válaszodat matematikailag indokold!)
A részpontszámokat azok kedvéért közöljük, akik ‐ későbbi versenyekre készülve ‐ az olimpiához hasonló feltételek mellett önállóan akarják megoldani a feladatokat. A ,,hivatalos'' megoldást és a mérési feladatot a KöMaL novemberi számában ismertetjük.
A feladatok kidolgozására 5 óra állt rendelkezésre. |
|
PDF | MathML 