Cím: A 48. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Szerző(k):  Gyenizse Gergõ ,  Hujter Bálint ,  Korándi Dániel ,  Lovász László Miklós ,  Nagy Csaba ,  Szûcs Gábor 
Füzet: 2007/október, 386 - 391. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

A szerkesztőség

 
1. Adottak az a1,a2,...,an valós számok. Mindegyik i-re (1≤i≤n) legyen
di=max{aj:1≤j≤i}-min{aj:i≤j≤n}
és legyen
d=max{di:1≤i≤n}.

(a) Bizonyítsuk be, hogy tetszőleges x1≤x2≤...≤xn valós számokra
max{|xi-ai|:1≤i≤n}≥d2.(*)

(b) Mutassuk meg, hogy vannak olyan x1≤x2≤...≤xn valós számok, amelyekre (*)-ban az egyenlőség áll fenn.
 

 

Lovász László Miklós megoldása. (a) Mivel max{aj:1≤j≤i}≥ai, és min{aj:i≤j≤n}≤ai, nyilván di≥0. Jelöljön k egy olyan indexet, amelyre d=dk; hasonlóan, legyen aℓ=max{aj:1≤j≤k} és am=min{aj:k≤j≤n}. Tegyük fel, hogy a feladat állításával ellentétben léteznek olyan x1≤x2≤...≤xn valós számok, amelyekre |xi-ai|<d2, minden i≤n-re. Ekkor azonban az
aℓ-xℓ≤|xℓ-aℓ|<d2,xm-am≤|xm-am|<d2
egyenlőtlenségek összege: aℓ-am+xm-xℓ<d.
Másrészt ℓ≤k≤m miatt ℓ≤m, és ezért xm≥xℓ. Így viszont aℓ-am+xm-xℓ=dk+xm-xℓ≥d, ami az előbbi egyenlőtlenségnek ellentmond.
 

(b) Minden 1≤i≤n indexre legyen
xi=max{aj:1≤j≤i}+min{aj:i≤j≤n}2.
Ez az xi sorozat valóban növekedő, mivel az összeg mindkét tagja monoton növő az i függvényében: bővebb számhalmaz maximuma legalább akkora, mint a szűkebbé, egy halmazt szűkítve pedig a minimum ugyancsak nő. Az Ai=max{aj:1≤j≤i} és Bi=min{aj:i≤j≤n} jelölésekkel Ai≥ai≥Bi, di=Ai-Bi, így
xi-ai≤xi-Bi=Ai+Bi2-Bi=Ai-Bi2=di2,ai-xi≤Ai-xi=Ai-Ai+Bi2=Ai-Bi2=di2.
Tehát minden i-re |xi-ai|≤di2≤d2, azaz max{|xj-aj|:1≤j≤n}≤d2; az (a)-ban kapott általános becsléssel összevetve ez igazolja, hogy a választott xi számok mellett (*)-ban egyenlőség áll.
 
2. Tekintsünk öt olyan A, B, C, D, E pontot, amelyekre ABCD egy parallelogramma, BCED pedig egy húrnégyszög. Legyen ℓ egy, az A ponton átmenő egyenes. Tegyük fel, hogy ℓ a DC szakaszt az F belső pontban metszi, a BC egyenest pedig a G pontban. Tegyük fel továbbá, hogy EF=EG=EC. Bizonyítsuk be, hogy ℓ a DAB∢ szögfelezője.
 

 

Hujter Bálint megoldása. A BCED körülírt köre legyen k, a CG szakasz felezőpontja (egyben az E-ből CG-re állított merőleges talppontja) T, hasonlóan az FC felezőpontja (ami az E-ből FC-re állított merőleges talppontja) S, az E-ből a DB egyenesre emelt merőleges talppontja R, végül az ST és az AC egyenes metszéspontja R'.
Megmutatjuk, hogy R'=R, és ez a pont az ABCD parallelogramma középpontja.
Az S, T, R pontok egy egyenesen, a BCD háromszög E-hez tartozó Simson-egyenesén vannak. Alkalmazzunk 2-szeres nagyítást a C-ből; ennek során T képe G, S képe F. A Simson-egyenes képe ezért ℓ, így R' képe A; vagyis R' az AC szakasz felezőpontja. Az R' a DB szakasz felezőpontjaként a Simson-egyenesnek DB-vel alkotott metszéspontja, ezért egybeesik R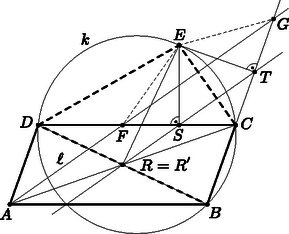-rel.
 

 

Az ER szakasz merőlegesen felezi a DB-t, azaz EB=ED. Így az EDF és EBC háromszögek két-két oldala (ED és EB, illetve EF és EC) egyenlő, és megegyeznek az EF és EC oldalakkal szemközti szögek is, hiszen EDF∢ és EBC∢ egyaránt ugyanahhoz az EC ívhez tartozó kerületi szög k-ban. Mivel DFE∢ az egyenlő szárú EFC háromszög alapon fekvő ‐ tehát hegyes ‐ EFC szögének külső szöge, azért DFE∢>90∘, és hasonlóan BCE∢>90∘. Tehát a tompaszögű EDF és EBC háromszögek egybevágóak; 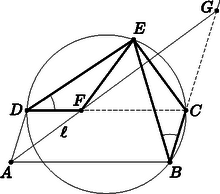DF=BC.
 

 

A parallelogramma párhuzamos oldalai miatt az ADF és a GCF háromszögek megfelelő szögei egyenlők, e két háromszög hasonló, ezért GCFC=ADDF. Így AD=BC=DF miatt GC=FC, vagyis az FCG (és a hozzá hasonló FDA) háromszög egyenlő szárú. A paralelogramma párhuzamos AB és DC oldalai révén az ABG háromszög is hasonló FCG-hez, így ugyancsak egyenlő szárú. Tehát DAF∢=DFA∢=CFG∢=CGF∢=FAB∢.
 
3. Egy matematikai verseny résztvevői közül némelyek barátok. A barátság mindig kölcsönös. Nevezzük a versenyzők egy halmazát klikknek, ha akárhogyan választva közülük kettőt, ők barátok. (Speciálisan bármelyik, kettőnél kevesebb versenyzőből álló halmaz klikk.) Egy klikk tagjainak a számát a klikk méretének fogjuk nevezni.
Ha tudjuk, hogy ebben a versenyben a legnagyobb méretű klikk mérete páros szám, bizonyítsuk be, hogy elhelyezhetjük a versenyzőket két teremben olymódon, hogy az egyik teremben található legnagyobb méretű klikk mérete egyenlő legyen a másik teremben található legnagyobb méretű klikk méretével.
 

 

Gyenizse Gergő megoldása. (1) Tekintsük a barátsági kapcsolatokat megjelenítő G gráf pontjainak egy olyan felosztását egymástól diszjunkt A és B halmazokra, amelyre az A-ban található maximális méretű klikk legalább akkora, mint a B-ben található, és a két méret különbsége a lehető legkisebb. Ha e különbség pozitív, akkor megmutatjuk, hogy az értéke 1. Ellenkező esetben az A pontjait egyesével rakjuk át B-be; egy pont áthelyezésével az A-beli maximális méretű klikk mérete legfeljebb 1-gyel csökken, a B-belié legfeljebb 1-gyel nő, így a különbség legfeljebb 2-vel csökken.
(2) Ha a feladat állítása hamis, akkor tehát az A-beli maximális méretű klikk mérete a, a B-belié pedig a-1. A G-ben nincs 2a-klikk, hiszen akkor abból vagy A-ba esne (a+1)-klikk, vagy B-be egy a-klikk. A feladat feltétele szerint ekkor viszont (2a-1)-klikk sem létezhet G-ben.
(3) Ha A-nak valamely x pontja nem tartozik hozzá egy A-beli a-klikkhez, akkor nincs olyan B-be eső (a-1)-klikk, amelynek minden pontja össze van kötve x-szel: ellenkező esetben ugyanis ezt az x pontot B-be áthelyezve az A-beli maximális klikkméret továbbra is a, a B-belié pedig szintén a-ra nőne.
(4) Megmutatjuk, hogy A-ban csupán egyetlen a-klikk található. Tegyük fel ugyanis, hogy van kettő; az egyiket jelölje C, és tegyük át A-nak a C-hez nem tartozó pontjait egyesével B-be. Ennek során B-ben ((3) szerint) nem keletkezhet (a-1)-nél nagyobb méretű klikk. Legyen p az a pontja A-nak, amelynek átrakása előtt még két a-klikk is található A-ban, utána viszont már csak egy, C. Jelölje továbbá q a C-nek egy olyan pontját, amely nincs összekötve p-vel. (Biztosan van ilyen pont, különben p a C-vel (a+1)-klikket alkotna.) Tegyük vissza a p után áthelyezett pontokat A-ba, a q pontot pedig rakjuk B-be. Azt állítjuk, hogy ekkor viszont A-ban és B-ben egyaránt a-1 a maximális klikkméret (ami ellentmondás). Valóban, q-val együtt csak C volt a-klikk az A-ban, ami q eltávolításával megszűnik. A (3) szerint q átkerülése előtt B-ben nem keletkezhet a-klikk, tehát csak úgy jöhetne végül létre, hogy q össze van kötve egy eredetileg is B-be tartozó (a-1)-klikk valamennyi pontjával. Ekkor viszont a következőképpen módosíthatunk: az eredeti A-ból csupán q kerüljön át B-be, ezzel ott létrejön egy a-klikk; A-ban viszont megmarad az a C-től különböző a-klikk, amely korábban p áttételével szűnt csak meg, ezért szükségképpen tartalmazza p-t. Így azonban nem tartalmazza q-t, hiszen p és q nincs összekötve. Ebben az elrendezésben tehát A és B maximális klikkmérete egyaránt a, ami ellentmondás.
(5) Jelölje a (4) szerint egyetlen A-beli a-klikket C, és helyezzük át az A összes, C-n kívüli pontját B-be; ennek során B maximális klikkmérete változatlanul a-1 marad. Ha viszont ezután C=A bármelyik y pontját B-be helyezzük, akkor A maximális klikkmérete (a-1)-re csökken, ezért ‐ eredeti indirekt feltevésünk értelmében ‐ B-ben a-klikk jön létre, méghozzá (4) szerint pontosan egy, jelöljük D-vel. A D-nek létezik olyan z pontja, ami az A-ból megmaradt (a-1)-klikk valamelyik pontjával nincs összekötve, hiszen ellenkező esetben a két halmaz (2a-1)-klikket alkotna G-ben, ellentmondva (2)-nek. Így azonban a z pontot az A-ba téve, ott továbbra is a-1 marad a maximális klikkméret, B-ben pedig (a-1)-re csökken, mivel D, az egyetlen a-klikk a z eltávolításával megszűnik. Ez ellentmond eredeti indirekt feltevésünknek.
 
4. Az ABC háromszögben a BCA∢ szögfelezője a körülírt kört az R pontban metszi (R≠C), a BC szakasz felezőmerőlegesét P-ben, az AC szakasz felezőmerőlegesét pedig Q-ban. A BC szakasz középpontja K, az AC szakasz középpontja pedig L. Bizonyítsuk be, hogy az RPK és RQL háromszögek területe egyenlő.
 

 

Szűcs Gábor megoldása. Elég belátni, hogy a 2. ábrán jelölt RPK, illetve RQL háromszögeknél kétszerte nagyobb területű RPB és RQA háromszögek területe egyenlő. Az ABC háromszög szögeit jelölje a szokásos módon α, β, γ; meghatározzuk a szóban forgó két háromszög szögeit. Az ACQ háromszög egyenlő szárú, ezért
QAC∢=QC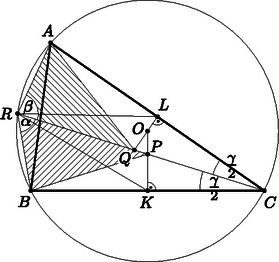A∢=γ2.
Így RQA∢=QCA∢+CAQ∢=γ, és ehhez teljesen hasonlóan adódik, hogy BPR∢=γ. A kerületi szögek tétele alapján ARQ∢=ABC∢=β, tehát
RAQ∢=180∘-ARQ∢-RQA∢=α.
Hasonlóan kaphatjuk, hogy a BPR háromszög szögei ugyancsak α, β, γ; tehát ARQ és BPR hasonló háromszögek. Mivel az AR és RB ívekhez tartozó kerületi szög egyaránt γ2, azért AR=RB: a két hasonló háromszögben a γ-val szemközti oldalak egyenlő hosszúak, így a két háromszög egybevágó, s ezért a területük is egyenlő.
 

 

1. ábra
 

 

 

2. ábra

 
5. Legyenek a és b pozitív egészek. Bizonyítsuk be, hogy ha 4ab-1 osztója (4a2-1)2-nek, akkor a=b.
 

 

Korándi Dániel megoldása. Legyen r és s egész szám. Ha a legnagyobb közös osztójuk d, akkor r=dr1 és s=ds1, ahol az r1 és s1 egészek egymáshoz relatív prímek. Tegyük fel, hogy r osztója s2-nek; ekkor dr1∣d2s12 miatt r1∣ds12. Mivel r1 relatív prím s12-hez is, r1 osztója d-nek. Ebből következik, hogy ha d osztója egy t egésznek, akkor r=dr1 osztója t2-nek.
4ab-1 és 4a2-1 legnagyobb közös osztója osztja a két szám különbségét, 4a(b-a)-t is, és mivel (mindkét eredeti számhoz hasonlóan) relatív prím 4a-hoz, osztója (b-a)-nak is. Az előbbi megjegyzés szerint tehát
4ab-1∣(b-a)2.
Megmutatjuk, hogy ez pozitív egész a-ra és b-re csak a=b esetén teljesül. Tegyük fel ezzel szemben, hogy b≠a; legyen például b>a. Ekkor
k=(b-a)24ab-1 pozitív egész.
Rendezve: 0=b2-2a(1+2k)b+(a2+k), azaz b gyöke az
x2-2a(1+2k)x+(a2+k)=0
másodfokú egyenletnek. Jelölje az egyenlet másik gyökét c; ekkor b+c=2a(1+2k) egész, ezért c is egész, és bc=a2+k>0 miatt c is pozitív. Valamivel pontosabban:
k=(b-a)24ab-1<(b-a)24ab-4a2=(b-a)4a,
ezért 2a(1+2k)<2a(1+b-a2a)=b+a, tehát 0<c<(b+a)-b=a. Erre a c egészre (b-hez hasonlóan)
k=(c-a)24ac-1,
azaz 4ca-1∣(a-c)2, és 0<c<a. Az a=b1>c=a1 pozitív egész számpár tehát ugyanazt az oszthatósági feltételt teljesíti, mint a b>a számpár, csak éppen b1<b. Az előbbi gondolatmenet így megismételhető b és a helyett b1-gyel és a1-gyel stb. Ezzel pozitív egészek végtelenül csökkenő b>b1>... sorozatát kapjuk, ami lehetetlen. Ez az ellentmondás igazolja állításunkat, és ezzel a feladat állítását is.
 
6. Legyen n pozitív egész. Tekintsük a háromdimenziós tér (n+1)3-1 pontjából álló alábbi halmazt:
S={(x,y,z):x,y,z∈{0,1,...,n},x+y+z>0}.
Határozzuk meg azon síkok számának a minimumát, amelyekre igaz az, hogy uniójuk tartalmazza az S halmaz minden pontját, de nem tartalmazza a (0,0,0) pontot.
 

 

Nagy Csaba megoldása. A feladat kérdésére a válasz: 3n. Ennyi sík valóban elegendő, például az x+y+z=1, x+y+z=2, ..., x+y+z=3n egyenletű síkok megfelelnek.
Megfordítva, tegyük fel, hogy néhány síkkal lefedtük S-et, az origót azonban nem. Megmutatjuk, hogy a síkok száma legalább 3n. Írjuk föl a síkok egyenletét ax+by+cz+d=0 alakban (ahol a, b, c nem mind nulla). Szorozzuk össze az egyenletek bal oldalán álló kifejezéseket; egy p(x,y,z) polinomot kapunk, ami S pontjaiban nulla, az origóban pedig nem. Igazolnunk kell, hogy p foka legalább 3n. Ehelyett a következő, általánosabb állítást látjuk be:
a, b, c természetes számok, és legyen
S(a,b,c)={(x,y,z)∣x∈{0,1,...,a},y∈{0,1,...,b},z∈{0,1,...,c},x+y+z>0}.
Ha az f(x,y,z) polinom S(a,b,c) pontjaiban nulla, a (0,0,0) pontban pedig nem, akkor a foka legalább a+b+c.
A bizonyítást az (a+b+c)-re vonatkozó indukcióval végezzük. Ha a+b+c=1, akkor a polinom legalább elsőfokú (azaz nem konstans), hiszen felvesz két különböző értéket. Ha a+b+c>1, akkor tekintsünk egy, a feltételeknek megfelelő f polinomot, a fokát jelölje t. Az a, b, c számok között létezik pozitív, legyen ez például a. Képezzük a g(x,y,z)=f(x+1,y,z)-f(x,y,z) polinomot. A g polinom foka nyilván legfeljebb t; viszont f(x+1,y,z)-ben és f(x,y,z)-ben ugyanazok a megfelelő t-edfokú tagok együtthatói, így ezek kiejtik egymást g-ben. A g foka ezért legfeljebb t-1. A g polinom az S(a-1,b,c) halmaz pontjaiban nulla, az origóban viszont nem nulla; az indukciós feltevés szerint tehát g foka legalább a-1+b+c, amiből t-1≥a-1+b+c, azaz t≥a+b+c következik.