Kezdőlap


Cím:	A 38. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Honyek Gyula , Vankó Péter
Füzet:	2007/november, 493 - 503. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Kettőscsillagok

1.1. kérdés. Periódusidő:

3 nap = 2, 6 \cdot 10^{5}

s.
Periódusidő

= \frac{2 π}{ω}

, innen a szögsebesség:

ω = 2, 4 \cdot 10^{- 5} \frac{1}{s}

1.2. kérdés. Nevezzük

α

-nak és

β

-nak az 1. ábrán² látható minimumokat:

\frac{I_{1}}{I_{0}} = α = 0, 90

és

\frac{I_{2}}{I_{0}} = β = 0, 63

. Ezek segítségével a következő összefüggéseket kapjuk:

\begin{matrix} \frac{I_{0}}{I_{1}} = 1 + {(\frac{R_{2}}{R_{1}})}^{2} {(\frac{T_{2}}{T_{1}})}^{4} = \frac{1}{α}, \frac{I_{2}}{I_{1}} = 1 - {(\frac{R_{2}}{R_{1}})}^{2} (1 - {(\frac{T_{2}}{T_{1}})}^{4}) = \frac{β}{α} . \end{matrix}

Ezekből az összefüggésekből a kérdéses arányok kiszámíthatóak:

\begin{matrix} \frac{R_{1}}{R_{2}} = \sqrt[]{\frac{α}{1 - β}} = 1, 56, \frac{T_{1}}{T_{2}} = \sqrt[4]{\frac{1 - β}{1 - α}} = 1, 39. \end{matrix}

2.1. kérdés. A Doppler-eltolódás alapján:

\frac{Δ λ}{λ_{0}} ≅ \frac{v}{c}

. A maximális és minimális hullámhosszak:

λ_{1, {max}_{}^{}} = 5897, 7

Å

λ_{1, {min}_{}^{}} = 5894, 1

Å

λ_{2, {max}_{}^{}} = 5899, 0

Å

λ_{2, {min}_{}^{}} = 5892, 8

Å

.
A maximális és minimális hullámhosszak különbsége:

Δ λ_{1} = 3, 6

Å

Δ λ_{2} = 6, 2

Å

.
Vegyük észre, hogy a Doppler-eltolódás a pályamenti sebességek kétszereséből adódik:

\begin{matrix} v_{1} = c \frac{Δ λ_{1}}{2 λ_{0}} = 9, 2 \cdot 10^{4} m/s, v_{2} = c \frac{Δ λ_{2}}{2 λ_{0}} = 1, 6 \cdot 10^{5} m/s . \end{matrix}

2.2. kérdés. Mivel a tömegközéppont nem mozog hozzánk képest:

\frac{m_{1}}{m_{2}} = \frac{v_{2}}{v_{1}} = 1, 7

2.3. kérdés. Felhasználva, hogy

r_{i} = \frac{v_{i}}{ω}

(

i = 1,2

), kiszámíthatjuk a csillagok pályájának sugarát:

r_{1} = 3, 8 \cdot 10^{9}

m és

r_{2} = 6, 5 \cdot 10^{9}

2.4. kérdés.

r = r_{1} + r_{2} = 1, 0 \cdot 10^{10}

3.1. kérdés. A gravitációs erő megegyezik a tömeg és a centripetális gyorsulás szorzatával:

\begin{matrix} G \frac{m_{1} m_{2}}{r^{2}} = m_{1} \frac{v_{1}^{2}}{r_{1}} = m_{2} \frac{v_{2}^{2}}{r_{2}} . \end{matrix}

Ennek alapján

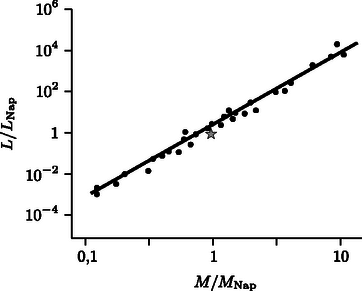
\begin{matrix} m_{1} = \frac{r^{2} v_{2}^{2}}{G r_{2}} = 6 \cdot 10^{30} kg, m_{2} = \frac{r^{2} v_{1}^{2}}{G r_{1}} = 3 \cdot 10^{30} kg. \end{matrix}

4.1. kérdés. A grafikon alapján világosan látszik, hogy a pontokra illeszthető egyenes meredeksége egy értékes jegy pontossággal

α = 4

4.2. kérdés. Az előző részfeladat eredménye alapján:

\begin{matrix} L_{i} = L_{Nap} {(\frac{M_{i}}{M_{Nap}})}^{4} . \end{matrix}

Így

L_{1} = 3 \cdot 10^{28}

W és

L_{2} = 4 \cdot 10^{27}

4.3. kérdés. A rendszer teljes kisugárzott teljesítménye egy

d

sugarú gömb mentén oszlik el egyenletesen, és hozza létre az észlelhető

I_{0}

intenzitást:

\begin{matrix} I_{0} = \frac{L_{1} + L_{2}}{4 π d^{2}}, ebből d = \sqrt[]{\frac{L_{1} + L_{2}}{4 π I_{0}}} = 10^{18} m = 100 fényév. \end{matrix}

4.4. kérdés.

θ ≅ tg θ = \frac{r}{d} = 10^{- 8}

rad.

4.5. kérdés. Egy tipikus optikai hullámhossz:

λ_{0} ≅ 500

nm. Mivel egy távcső szögfelbontása kb.

λ_{0} / D

, innen

D ≳ \frac{d λ_{0}}{r} \approx 50

2. feladat. Légzsák

1.1. kérdés. A kondenzátorlemezre felírva a Gauss-törvényt megkapjuk a térerősséget:

E = \frac{Q}{ε_{0} A}

. A térerősséget a két kondenzátorlemezen lévő töltés együttesen hozza létre, így mindkét lemez hozzájárulása

\frac{1}{2} E

. Ennek alapján a lemezek közt ható erő:

\begin{matrix} F_{e} = \frac{1}{2} E Q = \frac{Q^{2}}{2 ε_{0} A} . \end{matrix}

1.2. kérdés. A Hooke-törvény alapján a rugóerő:

F_{m} = - k x

. Az előző kérdésben levezettük a lemezek közt ható elektromos erőt:

F_{e} = \frac{Q^{2}}{2 ε_{0} A}

. A rendszer egyensúlyában

F_{m} + F_{e} = 0

, amiből

x = \frac{Q^{2}}{2 ε_{0} A k}

1.3. kérdés. A térerősség a kondenzátorlemezek között homogén, így a lemezek közötti

V

potenciálkülönbség egyszerűen számolható:

V = E (d - x)

. Behelyettesítve az előző részekben kapott eredményeket, kapjuk:

\begin{matrix} V = \frac{Q d}{ε_{0} A} (1 - \frac{Q^{2}}{2 ε_{0} A k d}) . \end{matrix}

1.4. kérdés. A

C

kapacitás a töltés és a potenciálkülönbség hányadosa:

C = \frac{Q}{V}

. Felhasználva az előző kérdésre kapott eredményt:

\begin{matrix} \frac{C}{C_{0}} = {(1 - \frac{Q^{2}}{2 ε_{0} A k d})}^{- 1} . \end{matrix}

1.5. kérdés. A rugóban tárolt mechanikai energia

U_{m} = \frac{1}{2} k x^{2}

, a kondenzátorban tárolt elektromos energia pedig

U_{E} = \frac{1}{2} \frac{Q^{2}}{C}

. Így a rendszerben tárolt teljes energia

\begin{matrix} U = \frac{Q^{2} d}{2 ε_{0} A} (1 - \frac{Q^{2}}{4 ε_{0} A k d}) . \end{matrix}

2.1. kérdés. Adott

x

érték esetén az egyes kondenzátorok töltése egyszerűen számolható:

\begin{matrix} Q_{1} = V C_{1} = \frac{ε_{0} A V}{d - x}, Q_{2} = V C_{2} = \frac{ε_{0} A V}{d + x} . \end{matrix}

2.2. kérdés. Ne felejtsük el, hogy két kondenzátorunk van. Felhasználva az 1.1. kérdésre kapott választ, az egyes kondenzátorokban fellépő erő

\begin{matrix} F_{1} = \frac{Q_{1}^{2}}{2 ε_{0} A}, F_{2} = \frac{Q_{2}^{2}}{2 ε_{0} A} . \end{matrix}

Mivel a két erő ellentétes irányú, az eredő erő

\begin{matrix} F_{e} = F_{1} - F_{2} = \frac{ε_{0} A V^{2}}{2} (\frac{1}{{(d - x)}^{2}} - \frac{1}{{(d + x)}^{2}}) . \end{matrix}

2.3. kérdés. Elhanyagolva az

x^{2}

-rendű tagokat, kapjuk:

\begin{matrix} F_{e} = \frac{2 ε_{0} A V^{2}}{d^{3}} x . \end{matrix}

2.4. kérdés. Két,

k

rugóállandójú rugó van sorba kapcsolva, így az eredő mechanikai erő

F_{m} = - 2 k x

. Az elektromos és a mechanikai erő ellentétes irányú, így, felhasználva az előző kérdésre kapott eredményt, az eredő erő

\begin{matrix} F = F_{m} + F_{e} = - 2 (k - \frac{ε_{0} A V^{2}}{d^{3}}) x, ebből pedig k_{eff} = 2 (k - \frac{ε_{0} A V^{2}}{d^{3}}) . \end{matrix}

2.5. kérdés. Felhasználva Newton II. törvényét és az előző eredményt

\begin{matrix} a = - \frac{2}{m} (k - \frac{ε_{0} A V^{2}}{d^{3}}) x . \end{matrix}

3.1. kérdés. Írjuk fel az áramkörre a Kirchhoff-törvényeket!

\begin{matrix} \frac{Q_{K}}{C_{K}} + V - \frac{Q_{2}}{C_{2}} = 0, - \frac{Q_{K}}{C_{K}} + V - \frac{Q_{1}}{C_{1}} = 0, Q_{2} - Q_{1} + Q_{K} = 0. \end{matrix}

Felhasználva, hogy

V_{K} = \frac{Q_{K}}{C_{K}}

, kapjuk:

\begin{matrix} V_{K} = V \frac{\frac{2 ε_{0} A x}{d^{2} - x^{2}}}{C_{K} + \frac{2 ε_{0} A d}{d^{2} - x^{2}}} . \end{matrix}

3.2. kérdés. Elhanyagolva az

x^{2}

-rendű tagokat, kapjuk:

\begin{matrix} V_{K} = V \frac{2 ε_{0} A x}{d^{2} C_{K} + 2 ε_{0} A d} . \end{matrix}

4.1. kérdés. Az elektromos és a mechanikai erő hányadosa

\begin{matrix} \frac{F_{e}}{F_{m}} = \frac{ε_{0} A V^{2}}{k_{eff} d^{3}} . \end{matrix}

Behelyettesítve a numerikus értékeket

\begin{matrix} \frac{F_{e}}{F_{m}} = 7, 6 \times 10^{- 9} . \end{matrix}

Az elektromos erők valóban elhanyagolhatók a rugóerők mellett.

4.2. kérdés. Az előzőek szerint elegendő a rugóerőt figyelembe vennünk:

F = 2 k x

. Így a gyorsuló (lassuló) rendszerben a mozgó lemez egyensúlyi elmozdulása

x = \frac{m a}{2 k}

. A maximális elmozdulás ennek éppen kétszerese, hiszen a mozgó lemez túllendül az egyensúlyi helyzeten:

\begin{matrix} x_{{max}_{}^{}} = 2 x, x_{{max}_{}^{}} = \frac{m a}{k} . \end{matrix}

4.3. kérdés. Ha a gyorsulás

a = g

, a maximális elmozdulás

\begin{matrix} x_{{max}_{}^{}} = \frac{m g}{k} . \end{matrix}

Továbbá felhasználva a 3.2. kérdésre kapott eredményt:

\begin{matrix} V_{K} = V \frac{2 ε_{0} A x_{{max}_{}^{}}}{d^{2} C_{K} + 2 ε_{0} A d} . \end{matrix}

Kifejezve

C_{K}

-t, és felhasználva, hogy

V_{K} = 0, 15

\begin{matrix} C_{K} = \frac{2 ε_{0} A}{d} (\frac{V x_{{max}_{}^{}}}{V_{K} d} - 1), C_{K} = 8, 0 \times 10^{- 11} F. \end{matrix}

4.4. kérdés. Legyen

ℓ

a vezető feje és a kormány közötti távolság. Ennek becsült értéke

ℓ = 0, 4

m ‐ 1 m.
Abban a pillanatban, amikor a lassulás elkezdődik, a vezető fejének az autóhoz viszonyított relatív sebessége nulla.

Δ v (t = 0) = 0

, így

\begin{matrix} ℓ = \frac{1}{2} g t_{1}^{2}, t_{1} = \sqrt[]{\frac{2 ℓ}{g}}, t_{1} = 0,3 s ‐ 0,5 s. \end{matrix}

4.5. kérdés. A

t_{2}

idő a harmonikus rezgést végző lemez periódusidejének fele:

t_{2} = \frac{T}{2}

, a periódusidő:

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{k}}, \end{matrix}

így

t_{2} = 0, 019

s.
Mivel

t_{1} > t_{2}

, a légzsák időben aktiválódik.

Megjegyzés a feladathoz: A gyakorlatban valóban ilyen elven működő gyorsulásmérők aktiválják az autók légzsákját. A valóságos és a feladatban szereplő eszközök között a legfontosabb különbség a méretekben van! A kereskedelemben kapható gyorsulásérzékelők integrált áramköri technológiával készülnek, a miniatürizált mechanikai alkatrészek és az elektronika ugyanazon az egy-két mm

^{2}

felületű félvezető csipen kerülnek kialakításra. Az apró és olcsó (néhány dolláros) eszközöket egyre több helyen használják rezgések mérésére és szabályozására; segítségükkel például csökkenthető a mosógépek centrifugálás közben fellépő rezonanciája.

3. feladat. Hawking-sugárzás

1.1. kérdés. Bármilyen alkalmas egyenlet felhasználásával megkaphatjuk a kérdéses mennyiségek dimenzióját. Például a következő kínálkozó lehetőségekkel élhetünk:
I) A Planck-összefüggés alapján:

\begin{matrix} h ν = E \Rightarrow [h] [ν] = [E] \Rightarrow [h] = [E] \cdot {[ν]}^{- 1} = M L^{2} T^{- 1} . \end{matrix}

II)

[c] = L T^{- 1}

.
III) A tömegvonzási törvény alapján:

\begin{matrix} F = γ \frac{m_{1} \cdot m_{2}}{r^{2}} \Rightarrow [G] = [F] {[r]}^{2} {[m]}^{- 2} = M^{- 1} L^{3} T^{- 2} . \end{matrix}

IV) Az ekvipartíció tétel segítségével:

E = \frac{1}{2} k_{B} θ

, ahol

θ

-val jelöltük a hőmérsékletet. Ennek alapján

[k_{B}] = [E] {[θ]}^{- 1} = M L^{2} T^{- 2} K^{- 1}

1.2. kérdés. Például a Stefan‐Boltzmann-törvény felhasználásával:

\begin{matrix} \frac{Teljesítmény}{Felület} = σ \cdot θ^{4}, \end{matrix}

amiből

[σ] K^{4} = [E] L^{- 2} T^{- 1} \Rightarrow [σ] = M T^{- 3} K^{- 4}

1.3. kérdés. Egy számfaktortól eltekintve a Stefan‐Boltzmann-állandó a következő alakban írható fel:

σ = h^{α} c^{β} G^{γ} k_{B}^{δ}

, ahol

α

β

γ

és

δ

értékét dimenzióanalízissel állapítjuk meg:

[σ] = {[h]}^{α} {[c]}^{β} {[G]}^{γ} {[k_{B}]}^{δ}

, ahol például

[σ] = M T^{- 3} K^{- 4}

. Szép sorjában írjuk be az összes dimenziót:

\begin{matrix} M T^{- 3} K^{- 4} & = {(M L^{2} T^{- 1})}^{α} {(L T^{- 1})}^{β} {(M^{- 1} L^{3} T^{- 2})}^{γ} (M L^{2} T^{- 2} K^{- 1}) = \\ = M^{α - γ + δ} L^{2 α + β + 3 γ + 2 δ} T^{- α - β - 2 γ - 2 δ} K^{- δ} . \end{matrix}

A hatványkitevők egybevetéséből a következő egyenletrendszert kapjuk:

\begin{matrix} \begin{matrix} α - γ + δ & = 1 \\ 2 α + β + 3 γ + 2 δ & = 0 \\ - α - β - 2 γ - 2 δ & = - 3 \\ - δ & = - 4 \end{matrix}} \Rightarrow \begin{matrix} α & = - 3, \\ β & = - 2, \\ γ & = 0, \\ δ & = 4, \end{matrix} vagyis σ = \frac{k_{B}^{4}}{c^{2} h^{3}} . \end{matrix}

2.1. kérdés. Az eseményhorizont

A

területe a fekete lyuk

m

tömegétől, a

c

fénysebességtől és a

G

egyetemes gravitációs állandótól függ:

A = G^{α} c^{β} m^{γ}

. A dimenzióanalízis módszere már a könyökünkön jön ki:

\begin{matrix} = {[G]}^{α} {[c]}^{β} {[m]}^{γ} \Rightarrow \\ \Rightarrow L^{2} & = {(M^{- 1} L^{3} T^{- 2})}^{α} {(L T^{- 1})}^{β} {(M)}^{γ} = M^{- α + γ} L^{3 α + β} T^{- 2 α - β} . \end{matrix}

Most csak három ismeretlent tartalmaz az egyenletrendszer:

\begin{matrix} \begin{matrix} - α + γ & = 0 \\ 3 α + β & = 2 \\ - 2 α - β & = 0 \end{matrix}} \Rightarrow \begin{matrix} α & = 2, \\ β & = - 4, \\ γ & = 2, \end{matrix} vagyis A = \frac{m^{2} G^{2}}{c^{4}} . \end{matrix}

2.2. kérdés. Az entrópia

d S = d Q / θ

termodinamikai definíciója (

d Q

a hőközlés mértéke,

θ

pedig a rendszer abszolút hőmérséklete) alapján az entrópia dimenziója:

[S] = [E] {[θ]}^{- 1} = M L^{2} T^{- 2} K^{- 1}

2.3. kérdés. Az

η

állandó dimenzióját Bekenstein nyomán (

η = S / A

), valamint az alapvető fizikai állandók (

h

c

G

és

k_{B}

) függvényeként így fejezhetjük ki:

\begin{matrix} = [S] {[A]}^{- 1} = M T^{- 2} K^{- 1}, \\ [η] & = {[G]}^{α} {[h]}^{β} {[c]}^{γ} {[k_{B}]}^{δ} = M^{- α + β + δ} L^{3 α + 2 β + γ + 2 δ} T^{- 2 α - β - γ - 2 δ} K^{- δ} . \end{matrix}

A hatványkitevők összevetése megint négyismeretlenes egyenletrendszerrel örvendeztet meg minket, ami azonban csak három ismeretlennel bír:

\begin{matrix} \begin{matrix} - α + β + δ & = 1 \\ 3 α + 2 β + γ + 2 δ & = 0 \\ - 2 α - β - γ - 2 δ & = - 2 \\ δ & = 1 \end{matrix}} \Rightarrow \begin{matrix} α & = - 1, \\ β & = - 1, \\ γ & = 3, \\ δ & = 1, \end{matrix} vagyis η = \frac{c^{3} k_{B}}{G h} . \end{matrix}

A továbbiakban már nem kell használnunk a dimenzióanalízis módszerét, ami nagy öröm, mert mostanra még a legelszántabbak is valószínűleg megcsömörlöttek tőle.

3.1. kérdés. A termodinamika első főtétele alapján

d E = d Q + d W

, ahol közelítésként feltesszük, hogy

d W = 0

. Az entrópia

d S = d Q / θ

definícióját felhasználva ezt kapjuk:

d E = θ_{H} d S + 0

.
Használjuk fel, hogy

S = \frac{G k_{B}}{c h} m^{2}

E = m c^{2}

Így a fekete lyuk Hawking-hőmérsékletére a következő összefüggést kapjuk:

\begin{matrix} θ_{H} = \frac{d E}{d S} = {(\frac{d S}{d E})}^{- 1} = c^{2} {(\frac{d S}{d m})}^{- 1} . \end{matrix}

Elvégezve a deriválást, megkapjuk a végeredményt:

\begin{matrix} θ_{H} = (\frac{1}{2}) \frac{c^{3} h}{G k_{B}} \cdot \frac{1}{m} . \end{matrix}

Megjegyezzük, hogy a végeredményben található

1 / 2

-es faktornak nincs jelentősége, elhagyható, csak a deriválás miatt maradt az összefüggésben.

3.2. kérdés. A Stefan‐Boltzmann-törvény az egységnyi felületre jutó kisugárzott teljesítményt adja meg. Figyelembe véve az

E = m c^{2}

összefüggést is, a következő egyenleteket írhatjuk fel:

\begin{matrix} \begin{matrix} \frac{d E}{d t} & = - σ θ_{H}^{4} A \\ σ & = \frac{k_{B}^{4}}{c^{2} h^{3}} \\ A & = \frac{m^{2} G^{2}}{c^{4}} \\ E & = m c^{2} \end{matrix}} \Rightarrow c^{2} \frac{d m}{d t} = - \frac{k_{B}^{4}}{c^{2} h^{3}} {(\frac{c^{3} h}{2 G k_{B}} \cdot \frac{1}{m})}^{4} \frac{m^{2} G^{2}}{c^{4}} . \end{matrix}

Az egyszerűsítések elvégzése után:

\begin{matrix} \frac{d m}{d t} = - \frac{1}{16} \frac{c^{4} h}{G^{2}} \cdot \frac{1}{m^{2}} . \end{matrix}

3.3. kérdés. A változók szétválasztásával a következő integrált végezhetjük el:

\begin{matrix} \frac{d m}{d t} = - \frac{1}{16} \frac{c^{4} h}{G^{2}} \frac{1}{m^{2}} \Rightarrow \int m^{2} d m = - \int \frac{c^{4} h}{16 G^{2}} d t \Rightarrow m^{3} (t) - m^{3} (0) = - \frac{3 c^{4} h}{16 G^{2}} t . \end{matrix}

Amikor a fekete lyuk

t = t^{*}

-kor teljesen elpárolog:

\begin{matrix} m (t^{*}) = 0 \Rightarrow t^{*} = \frac{16 G^{2}}{3 c^{4} h} m^{3} . \end{matrix}

3.4. kérdés. A fekete lyuk

C_{V}

hőkapacitása megmutatja, hogy a

θ

hőmérséklet egységnyi megváltozásához mekkora

E

energiaváltozás tartozik:

\begin{matrix} \begin{matrix} C_{V} & = \frac{d E}{d θ} \\ E & = m c^{2} \\ θ & = \frac{c^{3} h}{2 G k_{B}} \frac{1}{m} \end{matrix}} \Rightarrow C_{V} = - \frac{2 G k_{B}}{c h} m^{2} . \end{matrix}

4.1. kérdés. Újra a Stefan‐Boltzmann-törvény adja meg a fekete lyuk egységnyi felületének energiaveszteségi ütemét. A fekete lyuk kozmikus háttérsugárzás miatti energia nyereségét egy hasonló összefüggés írja le. Ezt úgy láthatjuk be, hogy termikus egyensúlyban a teljes energia változásnak el kell tűnnie. Ebből az következik, hogy az energia nyereség ütemét a Stefan‐Boltzmann-törvénnyel teljesen megegyező formula jellemzi:

\begin{matrix} \begin{matrix} \frac{d E}{d t} & = - σ θ^{4} A + σ θ_{B}^{4} A \\ E & = m c^{2} \end{matrix}} \Rightarrow \frac{d m}{d t} = - \frac{h c^{4}}{16 G^{2}} \frac{1}{m^{2}} + \frac{G^{2}}{c^{8} h^{3}} {(k_{B} θ_{B})}^{4} m^{2} . \end{matrix}

4.2. kérdés. Vegyük a

\frac{d m}{d t} = 0

esetet:

\begin{matrix} - \frac{h c^{4}}{16 G^{2}} \frac{1}{m^{* 2}} + \frac{G^{2}}{c^{8} h^{3}} {(k_{B} θ_{B})}^{4} m^{* 2} = 0, amiből m^{*} = \frac{c^{3} h}{2 G k_{B}} \frac{1}{θ_{B}} . \end{matrix}

4.3. kérdés.

\begin{matrix} θ_{B} = \frac{c^{3} h}{2 G k_{B}} \frac{1}{m^{*}} \Rightarrow \frac{d m}{d t} = - \frac{h c^{4}}{16 G^{2}} \frac{1}{m^{2}} (1 - \frac{m^{4}}{m^{* 4}}) . \end{matrix}

4.4. kérdés. Használjuk fel a 4.2. és a 3.1. részkérdésekre adott válaszeredményeket:

\begin{matrix} m^{*} = \frac{c^{3} h}{2 G k_{B}} \frac{1}{θ_{B}} és θ^{*} = \frac{c^{3} h}{2 G k_{B}} \frac{1}{m^{*}} = θ_{B} . \end{matrix}

Úgy is érvelhetünk, hogy

m^{*}

felel meg a termikus egyensúlynak. Így

m = m^{*}

esetén a fekete lyuk hőmérséklete

θ_{B}

. Az is elfogadható megoldás, hogy termikus egyensúly esetén

\begin{matrix} \frac{d E}{d t} = - σ (θ^{* 4} - θ_{B}^{4}) A = 0, amiből θ^{*} = θ_{B} . \end{matrix}

4.5. kérdés. A 4.3. eredmény alapján megmutatható, hogy az egyensúly instabil:

\begin{matrix} \frac{d m}{d t} = - \frac{h c^{4}}{16 G^{2}} \frac{1}{m^{2}} (1 - \frac{m^{4}}{m^{* 4}}) \Rightarrow \begin{matrix} m > m^{*} \\ m < m^{*} \end{matrix} \Rightarrow \begin{matrix} \frac{d m}{d t} > 0. \\ \frac{d m}{d t} < 0. \end{matrix} \end{matrix}

Kónya Gábor (aki maximális pontszámra írta meg az elméleti feladatok megoldását) a következő kiegészítéssel látta el dolgozatát a diákolimpián. Munkáját, amelyben dimenzióanalízis nélkül, alapvető fizikai megfontolások segítségével vezeti le a Hawking-probléma kevéssé ismert formuláit, változtatás nélkül közöljük.

A (m)

θ_{H} (m)

S (m)

képletek egy alternatív levezetése:
Vegyünk egy

p

impulzusú fotont a fekete lyukban, a középponttól

r

távolságra. A foton teljes energiája:

\begin{matrix} p c - G \frac{\frac{p}{c} m}{r} \leq 0 \Rightarrow r \leq \frac{G m}{c^{2}} . \end{matrix}

Az eseményhorizont sugara és felülete:

\begin{matrix} R = \frac{G m}{c^{2}} és A = 4 π R^{2} = 4 π \frac{G^{2} m^{2}}{c^{4}} \approx \frac{G^{2} m^{2}}{c^{4}} . \end{matrix}

R

sugarú gömbbe zárt foton impulzusát a határozatlansági relációból

p = \frac{ℏ}{R}

-nek becsülhetjük. Egy foton mozgási energiája:

\begin{matrix} p c = \frac{ℏ c}{R} = \frac{ℏ c^{3}}{G m} \approx \frac{h c^{3}}{G m} . \end{matrix}

A rendszer hőmérséklete:

θ_{H} \approx \frac{p c}{k} = \frac{h c^{3}}{G k m}

(ekvipartíció-tétel). A rendszer entrópiája:

\begin{matrix} S = \int \frac{d (m c^{2})}{θ_{H}} = \frac{G k}{h c} \cdot \frac{1}{2} m^{2} \approx \frac{G k}{h c} \cdot m^{2} . \end{matrix}

η = \frac{S}{A} = \frac{k c^{3}}{h G} = állandó

.
Az eredmények megegyeznek a dimenzióanalízissel kaphatókkal, de az

S \sim A

összefüggést bizonyítottuk, nem feltételeztük.

Kísérleti feladat

A kísérleti feladatban egy vasoxid (

Fe_{2}O_{3}

) nanorészecske-láncokat tartalmazó vékonyréteg-félvezető tiltottsáv-szélességét és vastagságát kellett meghatározni optikai módszerrel.
A tiltottsáv-szélesség a félvezetők és a szigetelők esetében a vegyérték sáv teteje és a vezetési sáv alja közti energiakülönbség. A vegyérték sáv teljesen be van töltve elektronokkal, a vezetési sáv pedig üres ‐ azonban a vegyérték sávból elektronok juthatnak a vezetési sávba, ha elegendő (legalább a tiltottsáv-szélességgel megegyező nagyságú) energiát kapnak.
A tiltottsáv-szélesség megméréséhez az átlátszó vékonyréteg fényelnyelő-képességét (abszorpcióját) kellett vizsgálniuk a versenyzőknek a mintán áthaladó fény spektrumának segítségével. Kicsit leegyszerűsítve azt mondhatjuk, hogy az abszorpciós spektrumon hirtelen ugrás (növekedés) figyelhető meg, amikor a foton energiája eléri a tiltottsáv-szélességet.
Kísérletileg bebizonyították, hogy a tiltottsáv-szélességnél kicsit nagyobb fotonenergiák esetében a következő összefüggés teljesül:

\begin{matrix} α h ν = A {(h ν - E_{g})}^{η}, \end{matrix}

(1)

ahol

α

a vékonyréteg abszorpciós együtthatója,

A

egy anyagfüggő (a vékonyréteg anyagától függő) állandó,

η

pedig a vékonyréteg anyagától és szerkezetétől függő abszorpciós mechanizmusból meghatározható állandó. (A vizsgált vékonyrétegre

A = 0, 071 eV^{1 / 2}/nm

és

η = 1 / 2

.) Az áteresztőképességet

α

értékével a jól ismert abszorpciós összefüggés kapcsolja össze:

\begin{matrix} T_{film} = e^{- α t}, \end{matrix}

ahol

t

a vékonyréteg vastagsága.
A mérési összeállításban (lásd ábra) egy

5'

pontossággal beállítható goniométerre (szögmérésre alkalmas eszköz egy rögzített és egy forgó karral) szerelt optikai ráccsal lehetett felbontani egy halogénlámpa fehér fényét. A mintán és a referenciának használt üveglemezen áthaladó fény erősségét fotoellenállás segítségével lehetett mérni. (A fotoellenállás elektromos ellenállása csökken, ha a rá eső fény intenzitása növekszik.)

A mérés elején a versenyzőknek hosszadalmas, bonyolult eljárással kellett beállítaniuk az egyes optikai elemeket, és meghatározniuk a spektrális felbontás pontosságát. Ezt követte a mérés elvégzése (a mintán, illetve az üres üveglemezen átmenő fény intenzitásának mérése a hullámhossz függvényében) és az adatok kiértékelése.
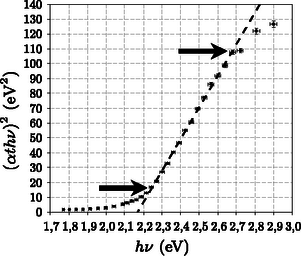
A kiértékeléshez az

x = h ν

és

y = {(α t h ν)}^{2}

értékpárokat kellett ábrázolni egy koordinátarendszerben, és a pontokra az (1) egyenletet kielégítő tartományban egyenest kellett illeszteni (lásd grafikon). Az (1) egyenletet

t

-vel megszorozva és négyzetre emelve kapjuk:

\begin{matrix} {(α t h ν)}^{2} = {(A t)}^{2} (h ν - E_{g}), \end{matrix}

amit összevetve

x

és

y

képletével:

\begin{matrix} y = {(A t)}^{2} (x - E_{g}) . \end{matrix}

Ennek alapján az illesztett egyenes paramétereiből már könnyen meghatározható az

E_{g}

tiltottsáv-szélesség és (

A

ismeretében) a vékonyréteg

t

vastagsága. A vékonyréteg előállítása nehezen reprodukálható, így az egyes mintákon

E_{g}

értéke 2 eV és 2,2 eV között,

t

értéke 70 nm és 200 nm között változott. (A rendezők a versenyre készített mind a 616 mintát végigmérték!)

¹Az elméleti feladatok szövegét múlt havi számunkban közöltük.

²KöMaL, 2007/7., 425. oldal.