Cím:	A 2006-2007. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2007/november, 461 - 471. oldal	PDF  |  MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. KEZDŐK   I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. Egy pozitív egész számot 4-gyel osztva 3, és 9-cel osztva 5 a maradék. Mennyi a maradék, ha a számot 36-tal elosztjuk?  (6 pont)   2. Hány olyan legfeljebb 5 jegyű, 5-tel nem osztható természetes szám van, amelynek minden jegye prím?  (6 pont)   3. Az $ABCD$ négyzet oldalainak hossza 30 cm. A $BC$ oldal felezőpontja $E$, a $CD$ oldal felezőpontja $F$. Számítsa ki a besötétített rész területét!  (6 pont) 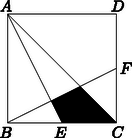    4. Egy derékszögű háromszög oldalainak hossza: befogói $a$ és $b$, átfogója $c$. Az átfogójához tartozó magasság hossza $m$. Igazolja, hogy: $c+m>a+b$.  (6 pont)   Második forduló   1. Hány olyan négyjegyű egész szám van a tízes számrendszerben, amelyben szerepel a 0 és az 1 számjegy is?  (6 pont)   2. Melyek azok a nem negatív $x$, $y$, és $z$ egész számok, melyekre teljesül, hogy: $\begin{array}{c}{\displaystyle {\left(x+y+z\right)}^2+{\left(x+y-z\right)}^2+{\left(x-y+z\right)}^2=40.}\end{array}$ (6 pont)   3. Egy szabályos ötszög kerülete 10 egység. Jelölje $AT$ az egyik szimmetriatengelyének az ötszögbe eső szakaszát, $h$ az $AT$, $R$ a köré írt és $r$ a beleírt kör sugarának hosszát! Igazolja, hogy: $\begin{array}{c}{\displaystyle \frac{1}{h}=R-r\mathrm{.}}\end{array}$ (8 pont)   4. Egy királyi palota alaprajza látható az alábbi ábrán. Tíz évvel ezelőtt az ábrán feltüntetett ajtók egyikét befalazták, ezt a változtatást tehát az ábra nem tükrözi. Három éve a király minden reggel bemegy a palotába a nyíllal megjelölt bejáraton, majd úgy sétál a termek között, hogy minden ajtón pontosan egyszer menjen keresztül. Végül leül a trónteremben és fogadja látogatóit. 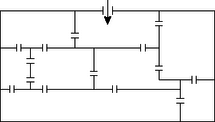    $a)$ Melyik ajtót falazták be? $b)$ Melyik terem a trónterem?  (10 pont)   5. Az $ABCD$ konvex négyszöget $AC$ átlójával felbontjuk két háromszögre. Bizonyítsa be, hogy ha az így keletkezett $ABC$ és $ADC$ háromszögek beírt körei érintik egymást, akkor az $ABD$ és $BCD$ háromszögek beírt körei is érintik egymást.  (10 pont)   Harmadik (döntő) forduló   1. Egy háromszög oldalai cm-ben mérve egész számok. Egyik oldala 2007 cm, a másik kettő legfeljebb ekkora. Hány ilyen háromszög van?   2. Egy négyzetrácsot 11 vízszintes és 11 függőleges vonal határoz meg. A vonalak metszéspontjai közül kijelölünk 20 pontot és bármelyik kettőt szakasszal kötünk össze. Mutassa meg, hogy e szakaszok között van négy azonos hosszúságú!   3. Legyen $A:=x^{10}\left(y^5-z^5\right)+y^{10}\left(z^5-x^5\right)+z^{10}\left(x^5-y^5\right)$. Igazolja, hogy ha $x$, $y$ és $z$ 11-gyel nem osztható pozitív egész számok, akkor $|A|$ osztható 11-gyel!   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló   Megegyezik az I. kategória első fordulós feladatsorával.   Második forduló   Megegyezik az I. kategória második fordulós feladatsorával.   Harmadik (döntő) forduló   1. Ábrázolja azoknak a $P\left(x;y\right)$ pontoknak a halmazát a síkon, amelyekre: $|y|\le 2-x^2$ és $|x|\le 2-y^2$ is teljesül! Igazolja, hogy e ponthalmaz területe több, mint 9 területegység!   2. Egy négyzetrácsot 11 vízszintes és 11 függőleges vonal határoz meg. A vonalak metszéspontjai közül kijelölünk 20 pontot és bármelyik kettőt szakasszal kötünk össze. Mutassa meg, hogy e szakaszok között van négy azonos hosszúságú!   3. Egy síkbeli zárt töröttvonal hossza 1 egység. Igazolja, hogy a töröttvonal által határolt tartomány lefedhető egy $\frac{1}{4}$ egység sugarú körrel!   III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló   Megegyezik az I. kategória második fordulós feladatsorával.   Második (döntő) forduló   1. Jelöljük $G\left(x\right)$-szel egy tízes számrendszerben felírt pozitív egész $x$ szám számjegyeinek összegét! Hány olyan $1\le x\le 2007$ pozitív egész szám van, melyhez létezik olyan $y>x$ pozitív egész szám, hogy $x+G\left(x\right)=y+G\left(y\right)$?   2. Definiáljuk az $a_n$ $\left(n\ge 0\right)$ sorozatot a következőképpen: $a_0:=0$, $a_1:=1$ és $n\ge 2$-re $a_n:=6a_{n-1}-a_{n-2}$. Bizonyítsa be, hogy $\begin{array}{c}{\displaystyle {\left(3-2\cdot \sqrt[]{2}\right)}^n\cdot a_{n+1}-{\left(3-2\cdot \sqrt[]{2}\right)}^{n+1}\cdot a_n=1}\end{array}$ minden $n\ge 0$-ra!   3. Adott egy egységnyi területű szabályos háromszög belsejében két pont úgy, hogy ez a két pont és a háromszög három csúcsa együtt 5 olyan pontot ad, amelyek közül semelyik három nem esik egy egyenesre. Tekintsük azokat a háromszögeket, amelyek csúcsai az említett 5 pont közül valók és jelöljük ezen háromszögek területei közül a legkisebbet $t_{\underset{}{\overset{}{\text{min}}}}$-nel! Mennyi $t_{\underset{}{\overset{}{\text{min}}}}$ lehetséges maximális értéke, és a két belső pont mely elhelyezkedése mellett érhető ez el?   HALADÓK I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók   Első (iskolai) forduló   1. Egy sakkversenyen mindenki mindenkivel egyszer játszik. Ha a résztvevők csak feleannyian lennének, akkor az eredetileg lejátszandó játszmák 24%-ára kerülne csak sor. Hány versenyző indult eredetileg a versenyen?   2. Az $ABCD$ téglalap $BC$ és $CD$ oldalának a $C$ csúcshoz közelebbi harmadolópontjai $P$, illetve $Q$. Az $AP$ és $AQ$ szakasszal három olyan részre osztottuk a téglalapot, amelyek közül kettőnek megegyezik a kerülete. Mekkora lehet ekkor a téglalap szomszédos oldalainak aránya?   3. Az ábrán látható szabályos hatszög $ED$ és $DC$ oldalainak $M$, illetve $N$ a felezőpontja. Milyen arányban osztják az $FC$ átlót a $T$ és $S$ po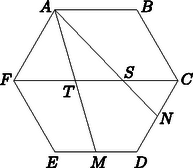ntok?     4. Egy kocka minden csúcsát két természetes számmal jelöltük meg, amelyek közül egyet egy betűvel eltakartunk. Így az egyik szám látható, a másik nem. Bármely csúcsnál lévő látható szám a csúccsal élszomszédos három, betűvel takart szám átlaga. Milyen számokat rejtenek a betűk? 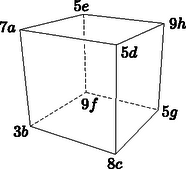    5. Egy gazda madárijesztő helyett hangágyúkkal próbálja távol tartani a madarakat földjétől. A hangágyún beállítható (egész másodpercekben) egy $t$ riasztási idő, és minden $t$ másodperc elteltével dördül egy nagyot. A $t$ idő 60 és 90 másodperc közé esik. A gazda különböző időre állította be két hangágyúját, hogy véletlenszerűnek tűnjön a dördülések ritmusa. Az első ágyú délelőtt 9 előtt 4 másodperccel szólalt meg, a másik pedig pontosan kilenckor. Később 10 óra után 4 másodperccel és 10 óra után 8 másodperccel is hallatszott egy-egy dördülés. Még később, valamikor 10 óra 10 perc és 10 óra 20 perc között a két eszköz pontosan egyszerre riasztott. Határozzuk meg másodpercre pontosan, mikor dördültek el egyszerre a hangágyúk 10 óra 10 perc és 10 óra 20 perc között!   Második forduló   1. Mennyi lesz a ${\left({\left({\left(\text{...}{\left(7^7\right)}^7\right)}^7\right)}^7\text{...}\right)}^7$ kifejezés utolsó jegye, ha 2006-szor végeztük el a 7. hatványra emelést?   2. Adjuk meg azokat a természetes számokból álló $\left(x;y\right)$ számpárokat, melyre teljesül, hogy $\begin{array}{c}{\displaystyle 2x^2+y^2=2xy+2x+84.}\end{array}$   3. Bizonyítsuk be, hogy ha egy téglalap átlói által bezárt kisebbik szög ${30}^{\circ }$, akkor a téglalap belső szögfelezői által közrefogott négyszög területe megegyezik a téglalap területével.   4. A Tour de Hongrie kerékpáros körverseny távja 777 km. A szervezők, hogy megkönnyítsék a versenyzők dolgát, valamennyi résztvevőnek egy olyan kijelzőt adtak, amelyen kilométerenként felvillan a már megtett és a még hátralévő távolság. Azaz az indulás pillanatában $\left(000;777\right)$, a célba érkezéskor $\left(777;000\right)$, közben például $\left(097;680\right)$ látható a kijelzőn. Hány esetben fordul elő, hogy a kijelzőn felvillanó számsorban pontosan kétféle számjegy található?   Harmadik (döntő) forduló   1. Bizonyítsuk be, hogy 1111-től 2007-ig bármely egész szám osztója az alábbi összegnek: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccccccc}\hfill {\displaystyle }& \hfill {\displaystyle 1\cdot }& \hfill {\displaystyle 2\cdot }& \hfill {\displaystyle 3\cdot }& \hfill {\displaystyle \text{...}}\hfill & {\displaystyle \cdot 896}\hfill & {\displaystyle +}\hfill \\ \hfill {\displaystyle +}& \hfill {\displaystyle 2\cdot }& \hfill {\displaystyle 3\cdot }& \hfill {\displaystyle 4\cdot }& \hfill {\displaystyle \text{...}}\hfill & {\displaystyle \cdot 897}\hfill & {\displaystyle +}\hfill \\ \hfill {\displaystyle +}& \hfill {\displaystyle 3\cdot }& \hfill {\displaystyle 4\cdot }& \hfill {\displaystyle 5\cdot }& \hfill {\displaystyle \text{...}}\hfill & {\displaystyle \cdot 898}\hfill & {\displaystyle +}\hfill \\ \hfill {\displaystyle +}& \multicolumn{1}{c}{{\displaystyle \text{...}}}& \hfill {\displaystyle }& \hfill {\displaystyle }& \hfill {\displaystyle }& \hfill {\displaystyle }\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle +}& \hfill {\displaystyle 1111\cdot }& \hfill {\displaystyle 1112\cdot }& \hfill {\displaystyle 1113\cdot }& \hfill {\displaystyle }\hfill & {\displaystyle \cdot 2006}\hfill & {\displaystyle }\hfill \end{array}}}\end{array}$   2. Az $R$ sugarú $AB$ átmérőjű kört belülről érinti az $r$ sugarú $k$ kör az $A$ pontban ($R>r$). Az $R$ sugarú kör $BC$ húrja az $E$ pontban érinti a $k$ kört. Ha a $BE$ és $CE$ szakasz mértani közepe megegyezik a két kör sugarának mértani közepével, akkor mekkora az $r:R$ arány értéke?   3. A Matematikai Kaszinóban a következő játékot játszhatjuk: 1-től 10 000-ig vannak számok egy urnában, ezek közül véletlenszerűen kihúznak egyet. Ha szép szám jött ki, kapunk $n$ forintot, ha nem, be kell fizetnünk 1 forintot. A Kaszinóban szépnek nevezik azokat az $a$ egész számokat, amelyek oszthatók negyedik gyökük egészrészével, tehát $\left[\sqrt[4]{a}\right]\mid a$. $\left(a\right)$ Hány szép szám van 1-től 10 000-ig? $\left(b\right)$ Melyik az a legkisebb egész $n$, amire érdemes játszani?   II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók   Első (iskolai) forduló   1. Melyik az a legnagyobb kettőhatvány, amivel a $2^{2005}+{10}^{2005}$ osztható?   2. Két párhuzamos egyenes mindegyikén prímszám számú pontot jelöltünk meg. A megjelölt pontok ‐ mint csúcsok ‐ által meghatározott összes négyszög száma kétszerese a megjelölt pontok által meghatározott háromszögek számának. Hány pontot jelöltünk meg az egyeneseken?   3. Egy kocka minden csúcsát két természetes számmal jelöltük meg, amelyek közül egyet egy betűvel eltakartunk. Így az egyik szám látható, a másik nem. Bármely csúcsnál lévő látható szám a csúccsal élszomszédos három, betűvel takart szám átlaga. Milyen számokat rejtenek a betűk?     4. A $k_1$ és $k_2$ körök kívülről érintik egymást. Az érintési ponton átmenő egyenes $k_1$-et a $P_1$, $k_2$-t a $P_2$ pontban metszi másodszor. Megrajzoltuk a $P_1$-en és $P_2$-n áthaladó, $k_1$-et érintő kört. Bizonyítsuk be, hogy ennek a körnek a sugara a $k_1$ és $k_2$ körök sugarának összegével egyenlő!   5. A Fiatal Matematikusok Konferenciájára 99 diák kapott meghívást. A résztvevők magyar, angol, német, olasz, francia, görög és török nemzetiségűek voltak. A szervezők észrevették, hogy nincs 8 különböző korú, azonos nemzetiségű résztvevő. Bizonyítsuk be, hogy van két azonos korú, nemű és nemzetiségű résztvevő a konferencián!   Második forduló   1. Határozza meg a következő kifejezés legkisebb és legnagyobb értékét a valós számok halmazán: $\begin{array}{c}{\displaystyle K=\frac{x+1}{x^2+1}\mathrm{.}}\end{array}$   2. Tekintsük az $N=1^2+2^3+3^4+4^5+\text{...}+{2006}^{2007}$ összeget! $a)$ Bizonyítsuk be, hogy $N$ nem négyzetszám. $b)$ Igazoljuk, hogy $N+4$ nem prímszám.   3. Az $AB$ alapú $ABC$ egyenlő szárú háromszög $A$ csúcsból induló súlyvonalát harmadolja a $B$ csúcsból induló magasság. Mekkora szögben látszik a háromszög $S$ súlypontjából az $AB$ alap?   4. A Tour de Hongrie kerékpáros körverseny távja 777 km. A szervezők, hogy megkönnyítsék a versenyzők dolgát, valamennyi résztvevőnek egy olyan kijelzőt adtak, amelyen kilométerenként felvillan a már megtett és a még hátralévő távolság. Tehát az indulás pillanatában $\left(000;777\right)$, a célba érkezéskor $\left(777;000\right)$, közben például $\left(097;680\right)$ látható a kijelzőn. Hány esetben fordul elő, hogy a kijelzőn felvillanó számsorban nincs két egyforma számjegy?   Harmadik (döntő) forduló   1. Legyen $\alpha$ az $x^2+px+q=0$ egyenlet egyik valós gyöke, $\beta$ pedig az $x^2-px-q=0$ egyik valós gyöke, ahol $p\mathrm{,}q\in \text{R}$ és $q\ne 0$. Bizonyítsuk be, hogy az $x^2-2px-2q=0$ egyenletnek van $\alpha$ és $\beta$ közé eső valós gyöke!   2. Rajzoljuk meg azokat a köröket, amelyek átmennek egy tetszőleges háromszög egyik csúcsán és a csúcsból induló oldalak csúcshoz közelebbi harmadolópontjain! Bizonyítsuk be, hogy van olyan kör, amelynek sugara a megrajzolt körök sugarának számtani közepe, és mindhárom kört érinti.   3. Tekintsük a szabályos $n$-szög csúcsai által meghatározott összes háromszöget! Mekkora lehet $n$ értéke, ha a háromszögek között pontosan ugyanannyi tompaszögű van, mint hegyesszögű?     III. kategória: Speciális tantervű osztályokban tanulók   Első (iskolai) forduló   1. Melyek azok az $x$ valós számok, amelyekre igaz, hogy $\begin{array}{c}{\displaystyle \frac{8}{\sqrt[]{x+6}-\sqrt[]{x-2}}\le 6-\sqrt[]{x+1}?}\end{array}$   2. Az $ABC$ háromszög $BM$ és $CN$ súlyvonalának metszéspontja $S$, és tudjuk, hogy $AMSN$ érintőnégyszög. Bizonyítsuk be, hogy az $ABC$ háromszög egyenlő szárú!   3. Egy egységnyi élű kocka alaplapja az $ABCD$ négyzet. A kocka $A_1$, $B_1$, $C_1$, $D_1$ csúcsaira teljesül, hogy $A{A}_1$, $B{B}_1$, $C{C}_1$ és $D{D}_1$ párhuzamosak. Az $A{C}_1$ testátló két harmadolópontja $P$ és $Q$. A $D_{1}P$ és a $D_{1}Q$ egyenes az $ABCD$ lap síkját a $K$, illetve az $E$ pontban metszi. Határozzuk meg az $AK$ és az $AE$ szakaszok hosszát!   4. Tekintsük azokat a pozitív egész számokat, amelyekre igaz, hogy számjegyeik összege és szorzata is $9^{2007}$. Igazoljuk, hogy egyetlen megfelelő szám számjegyeinek száma sem lehet négyzetszám.   5. Egy kör kerületét 10 darab piros és 12 darab kék pont ívekre bont. Ezekre az ívekre számokat írunk a következő módon: két piros pont közötti ívre 2-t, két kék pont közötti ívre $\frac{1}{2}$-et, egy piros és egy kék közti ívre 1-et. Mennyi lehet ezeknek a számoknak a szorzata a piros és kék pontok különböző elrendezése esetén?   Második (döntő) forduló   1. Jelölje $a_n$ a $\left(\genfrac{}{}{0ex}{}{2n}{1}\right)\mathrm{,}\left(\genfrac{}{}{0ex}{}{2n}{3}\right)\mathrm{,}\left(\genfrac{}{}{0ex}{}{2n}{5}\right)\mathrm{,}\text{...}\mathrm{,}\left(\genfrac{}{}{0ex}{}{2n}{2n-1}\right)$ számok legnagyobb közös osztóját! Mennyit ér az $\left\{a_1\mathrm{,}{a}_2\mathrm{,}{a}_3\mathrm{,}\text{...}\mathrm{,}{a}_{2007}\right\}$ halmaz legnagyobb eleme?   2. Tekintsük azokat a háromszögeket, amelyeknek oldalai $n-1$, $n$, $n+1$, ahol $n$  2-nél nagyobb egész szám! Ha $t_n$ jelöli az egyes háromszögek területét, akkor bizonyítsuk be, hogy a $\left\{t_n\right\}$ sorozat bármely tagjának végtelen sok egész számú többszöröse is tagja a sorozatnak.   3. Az $ABC$ hegyesszögű háromszög súlypontja $S$, az $AB$ és $AC$ oldalak felezőpontja $X$ és $Y$. Tudjuk, hogy az $AXY$ és $BCS$ háromszögek köréírt köre érinti egymást. Bizonyítsuk be, hogy az $ABC$ háromszög magasságpontját és köréírt körének középpontját összekötő szakasz merőleges az $A$-ból induló súlyvonalra!