Kezdőlap


Cím:	Megjegyzések a 2005. évi Eötvös-verseny 2. és 3. feladatának megoldásához
Szerző(k):	Gnädig Péter
Füzet:	2006/március, 177 - 181. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzések a 2005. évi Eötvös-verseny 2. és 3. feladatának megoldásához ¹

A 2. feladat a Huygens‐Fresnel-elv és némi (vektor)algebrai ismeret felhasználásával is megoldható. Tekintsük az ernyő valamely

R = (X, Y, S)

vektorral jellemzett pontját (

S = 3 m

a rács és az ernyő távolsága), valamint a lézerfénnyel megvilágított lap

r_{0} = (0,0,0)

és

r = (x, y,0)

vektorokkal megadott rácspontjait. Annak feltétele, hogy az

r_{0}

és az

r

rácspontokból kiinduló fény az

R

pontban erősítse egymást:

\begin{matrix} | R - r_{0} | - | R - r | = \sqrt[]{X^{2} + Y^{2} + S^{2}} - \sqrt[]{{(X - x)}^{2} + {(Y - y)}^{2} + S^{2}} = n λ, \end{matrix}

ahol

n

egész szám. Kihasználva, hogy

S ≫ X, Y ≫ x, y

, a fenti két négyzetgyök különbsége így is írható:

\begin{matrix} \sqrt[]{X^{2} + Y^{2} + S^{2}} - \sqrt[]{{(X - x)}^{2} + {(Y - y)}^{2} + S^{2}} = \\ = S {(1 + \frac{X^{2} + Y^{2}}{S^{2}})}^{1 / 2} - S {(1 + \frac{{(X - x)}^{2} + {(Y - y)}^{2}}{S^{2}})}^{1 / 2} \approx \frac{x X + y Y}{S} = n λ . \end{matrix}

Legyen például

x = d

és

y = 0

, vagyis tekintsük a rács önkényesen kiválasztott origójától jobbra elhelyezkedő,

a = (d,0,0)

vektorral megadott lyukból induló fényt. Az erősítés feltétele a fenti közelítésben:

\begin{matrix} d \cdot X = n_{1} λ S, \end{matrix}

ahol

n_{1}

egész szám. Hasonlóan felírhatjuk egy másik, a háromszögrács origójától ,,jobbra fölfelé'' elhelyezkedő,

b = (\frac{d}{2}, \frac{\sqrt[]{3}}{2} d,0)

vektorral megadott lyukra az erősítő interferencia feltételét:

\begin{matrix} \frac{d}{2} \cdot X + \frac{\sqrt[]{3}}{2} d \cdot Y = n_{2} λ S, \end{matrix}

ahol

n_{2}

ugyancsak egész szám.
Ha a fenti két feltétel teljesül, akkor nem csak a vizsgált két lyukpárra, hanem pl. a

2 a

3 a

2 b

3 b

, sőt, a háromszögrács tetszőleges

N_{1} a + N_{2} b

vektorral megadható pontjából induló elemi hullámra is igaz lesz erősítés feltétele, amennyiben

N_{1}

és

N_{2}

egészek.
A fenti egyenletekből álló rendszer megoldása: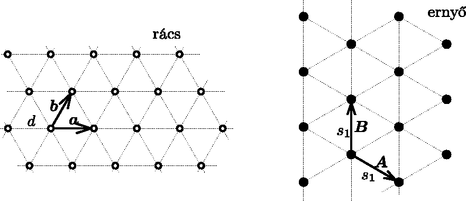

\begin{matrix} X = n_{1} \cdot \frac{S λ}{d}, Y = - n_{1} \cdot \frac{S λ}{\sqrt[]{3} d} + n_{2} \cdot \frac{2 S λ}{\sqrt[]{3} d}, \end{matrix}

amit vektor alakban így is felírhatunk:

\begin{matrix} (\begin{matrix} X \\ Y \end{matrix}) = n_{1} \cdot \frac{S λ}{d} (\begin{matrix} 1 \\ - 1 / \sqrt[]{3} \end{matrix}) + n_{2} \cdot \frac{S λ}{d} (\begin{matrix} 0 \\ 2 / \sqrt[]{3} \end{matrix}) = n_{1} \cdot A + n_{2} \cdot B . \end{matrix}

A

és

B

vektorok egymással

120^{\circ}

-os szöget zárnak be, nagyságuk ugyanakkora:

\begin{matrix} | A | = | B | = s_{1} = \frac{2}{\sqrt[]{3}} S \frac{λ}{d}, \end{matrix}

a belőlük egész együtthatós ,,lineáris kombinációval'' adódó pontrács tehát egy szabályos háromszögrács (1. ábra).

1. ábra

2. A feladat egy egyszerű geometriai módszerrel is megoldható. Tekintsünk először egy

D

rácsállandójú négyzetrácsban elhelyező lyukrendszer elhajlási képét. Ez az eset lényegében az optikai ráccsal egyenértékű: a rácsnégyzet mindkét oldalának megfelelő irányban

\begin{matrix} α_{k} \approx sin α_{k} = k \frac{λ}{D} \end{matrix}

szögben térülhet el a lézerfény, az

S

távol levő ernyőn tehát egy

s = \frac{S λ}{D}

rácsállandójú, az eredeti lyukelrendezéssel megegyező állású négyzetrács alakul ki.
Nyújtsuk meg képzeletben a lyukrendszert síkjának valamelyik iránya mentén az eredeti méretének

c

-szeresére. Könnyen végiggondolható, hogy ilyenkor az ernyőn az elhajlási kép is ugyanilyen irányban, de ellentétes módon deformálódik: az eredeti méretének

c

-ed részére zsugorodik. (Ha valamilyen irányban

c

-szer ritkábban helyezkednek el a lyukak, akkor a megfelelő útkülönbség

c

-szer kisebb elhajlási szög mellett alakulhat csak ki, és ez az ernyőn a megfelelő irányban

c

-szeres zsugorításnak felel meg.)
A 2. ábra bal oldali fele egy olyan négyzetrácsot mutat, amelyben a lyukak legkisebb távolsága (a rácsállandó)

\begin{matrix} D = d / \sqrt[]{2}, \end{matrix}

és a négyzetek egyik (

d

hosszúságú) átlója ,,vízszintesen'' helyezkedik el.

2. ábra

Ennek megfelelően az elhajlási kép (az ábra jobb oldai fele) egy olyan ‐ a szokásos elhelyezéshez képest ugyancsak

45^{\circ}

-ban elforgatott ‐ négyzetrács lesz, amelynek rácsállandója

\frac{S λ}{D}

, a négyzetek átlója tehát

\begin{matrix} l = \sqrt[]{2} L = \sqrt[]{2} \frac{S λ}{D} = 2 \frac{S λ}{d} \end{matrix}

hosszúságú.
Nyújtsuk meg most a rácsot az ábrán megjelölt ,,függőleges'' irányban

\sqrt[]{3}

-szorosára! Ekkor éppen a feladatunkban szereplő

d

rácsállandójú rácsot kapjuk (3. ábra bal oldala). Az ernyőn az elhajlási kép ugyancsak ,,függőlegesen''

\sqrt[]{3}

-ad részére összezsugorodik (lásd a 3. ábra jobb felét), és így

\begin{matrix} s = \frac{l}{\sqrt[]{3}} = \frac{2}{\sqrt[]{3}} \frac{S λ}{d} = 2 \sqrt[]{3} cm \end{matrix}

rácsállandójú, az eredeti lyukrácshoz képest

90^{\circ}

-kal elforgatott szabályos háromszögráccsá válik.

3. ábra

Az itt alkalmazott transzformációt (amely egyenest egyenesbe visz át, egy-egy egyenes mentén aránytartó, de nem szögtartó) a matematikában affin-transzformációnak nevezik.

A 3. feladat energetikai megfontolásokkal is megoldható. Ehhez először belátjuk, hogy a transzformátor tekercsein átfolyó áramok, a tekercseken eső feszültségek és a hálózati feszültség mind azonos fázisban rezegnek. Ez valóban igaz, hiszen a szekunder tekercset egy ohmos ellenállással zártuk, így a rajta átfolyó áram és a feszültsége között nincs fáziskülönbség. A primer és a szekunder feszültség is azonos fázisban változik (hiszen csak így lehet az arányuk minden pillanatban a menetszámoknak megfelelő

1 : 3

), és ugyanez igaz (terhelt transzformátornál) a primer- és a szekunderköri áramokra is. A primer körben tehát a tekercs feszültsége és az ohmos ellenálláson eső feszültség között nincs fáziskülönbség, és mivel az összegük minden pillanatban a hálózati feszültség, azzal is azonos fázisban kell legyenek.
Ha

I_{p}

-vel jelöljük a primer,

I_{sz}

-szel pedig a szekunder kör effektív áramerősségét, akkor (a 16. ábra jelöléseit követve) felírhatjuk, hogy a hálózat által leadott teljesítmény megegyezik a két kör ellenállásai által felvett teljesítménnyel:

\begin{matrix} U I_{p} = I_{p}^{2} \frac{R}{4} + I_{sz}^{2} R . \end{matrix}

Másrészt igaz, hogy az adott menetszám-arányú, jó minőségű, terhelt transzformátornál

U_{3} = 3 U_{2}

és

U_{2} \cdot I_{p} = U_{3} \cdot I_{sz}

, azaz

\begin{matrix} I_{sz} = \frac{1}{3} I_{p} . \end{matrix}

A fenti egyenletekből a szekunder kör áramára

\begin{matrix} I_{sz} = \frac{12}{13} \frac{U}{R}, \end{matrix}

a primer körben egy-egy izzó áramerősségére pedig

\begin{matrix} \frac{1}{3} I_{p} = \frac{9}{13} \frac{U}{R} \end{matrix}

adódik, amelyből a megoldásban közölt eredményekhez és következtetésekhez juthatunk, vagyis valamennyi izzó tűrhetően kell világítson.

¹A feladatok szövegét és a hivatalos megoldást lásd Radnai Gyula cikkében lapunk 168. oldalán.