Kezdőlap


Cím:	Beszámoló a 2005. évi Eötvös-versenyről
Szerző(k):	Radnai Gyula
Füzet:	2006/március, 168 - 177. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2005. október 14-én délután az ország 16 városában rendezte meg az Eötvös Loránd Fizikai Társulat azévi Eötvös-versenyét. Budapesten 50, Pécsett 12, Debrecenben és Szegeden 7‐7, Miskolcon 6, Kecskeméten 5, Veszprémben és Székesfehérváron 4‐4, Győrött 1 hazai és 3 külföldi, Egerben, Szekszárdon és Szombathelyen 3‐3, Békéscsabán, Nagykanizsán és Sopronban 1‐1 versenyző adott be dolgozatot. Nyíregyházán sajnos egyetlen főiskolai vagy középiskolai diák se jelent meg a verseny színhelyén. Összesen 108 hazai és 4 külföldi versenyző dolgozatát kellett értékelnie a versenybizottságnak (elnök: Radnai Gyula, tagok: Gnädig Péter, Honyek Gyula és Károlyházy Frigyes).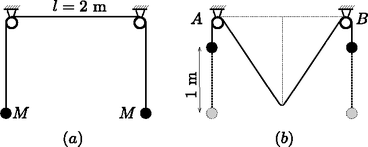
Ismertetjük a feladatokat és a feladatok helyes megoldását.

1. Két rögzített, egymástól

l = 2 m

távolságra levő csigán erős, de nem nyúlékony fonalat vezetünk át, és a végeire egy-egy

M = 1 kg

tömegű testet erősítünk az 1.

(a)

ábra szerint. (A fonal néhányszor 10 N terhelést bír ki szakadás nélkül. A csigák és a fonal tömege elhanyagolható.) Ha ujjunkkal lehúzzuk a fonal közepét úgy, hogy a két test

1

‐

1

méterrel megemelkedjék (1.

(b)

ábra), majd elengedjük, a fonal elpattan, amikor

A

és

B

között ,,kiegyenesedik''. Ha azonban úgy engedjük el, hogy előbb egy ugyancsak 1 kg tömegű testet erősítünk a fonal közepéhez, akkor a fonal a továbbiakban nem szakad el.

1. ábra

a)

Magyarázzuk meg a jelenséget!

b)

Mekkora erő feszíti a fonalat abban a pillanatban, amikor kiegyenesedik?

Megoldás.

a)

Azt kell észrevenni, hogy amikor a fonal kiegyenesedik, abban a pillanatban a fonalat két oldalról húzó testek már állnak. Rendkívül rövid idő alatt kell megállniuk, lefékeződniük arról a

v = \sqrt[]{2 g h} \approx 16

km/h sebességről, amire addigi mozgásuk (szabadesés) során felgyorsultak. (Itt és a továbbiakban

h = \frac{1}{2} l = 1 m

.) Ha a fékezést ,,pillanatszerűnek'' gondolnánk, vagyis a fékezés ideje

Δ t \to 0

lenne, akkor a testek gyorsulása és a fonalat feszítő

F

erő is minden határon túl nőne, ezért elpattanna a fonal.
A valóságban természetesen még a ,,nem nyúlékony'' fonal sem abszolút nyújthatatlan, hanem egy kicsit deformálható. Ehhez az alakváltozáshoz egy kicsiny, de véges

Δ t

idő szükséges, így a testek gyorsulása és ezzel együtt a fonalat feszítő erő ha nem is végtelenné, de nagyon naggyá válik. Mivel a fonal nem bír ki nagy erőt, elszakad.

b)

Ábrázoljuk a folyamat három jellemző állapotát! A 2.

(a)

ábrán a kezdőállapotot tüntettük fel, megjelölve közben a középső test egyensúlyi helyzetét is, amelyen maximális sebességgel átlendül. A 2.

(b)

ábrán a fonal középső része vízszintes, a középső test azonban még emelkedik fölfelé. A 2.

(c)

ábra azt a pillanatot mutatja, amikor a középső test éppen megáll. Ekkor ismét állnak a szélső testek is. (Persze elképzelhető, hogy a középső test fel se emelkedik a 2.

(b)

ábrán látható helyzetig, ezt a lehetőséget majd számítással kell ellenőriznünk.)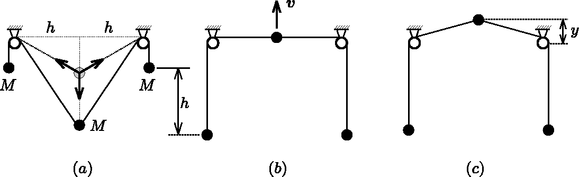

2. ábra

b)

kérdés megfogalmazása arra utal, hogy a fonal ki fog egyenesedni, tehát a középső test eljut a 2.

(b)

ábrán jelzett állapotba. Lesz-e ott sebessége? Ezt érdemes kiszámítanunk. Írjuk fel a munkatételt a 2.

(a)

helyzettől a 2.

(b)

-ig jelzett folyamatra! A szélső testek

h

utat süllyednek, a középső

h \sqrt[]{3}

utat emelkedik, ezért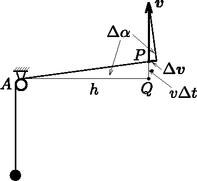

\begin{matrix} M g h - M g h \sqrt[]{3} + M g h = \frac{1}{2} M v^{2} . \end{matrix}

Felhasználtuk, hogy a 2.

(b)

helyzetben a szélső testek egy pillanatra megállnak, ezért csak a középső testnek lehet ekkor mozgási energiája. A felírt egyenletből a középső test sebessége:

v = \sqrt[]{2 g (2 - \sqrt[]{3}) h} > 0

. Tehát valóban emelkedik még a középső test. Meddig emelkedik? Ezt is kiszámíthatjuk, ha a 2.

(b)

és a 2.

(c)

állapotot hasonlítjuk össze energetikailag:

\begin{matrix} 2 M g (\sqrt[]{h^{2} + y^{2}} - h) + M g y = \frac{1}{2} M v^{2} . \end{matrix}

y

-ra nézve másodfokú egyenletté alakítható, melynek megoldásai:

y_{1} = - 1, 73 h

és

y_{2} = + 0, 22 h

. (Az első gyök nyilván a kezdőállapotot adja meg, a 2.

(c)

állapotnak

y_{2}

felel meg.)

3. ábra

Hogy válaszolni tudjunk a feladat

b)

kérdésére, vizsgáljuk meg tüzetesen a 2.

(b)

ábrán látható helyzetet! Ebben a pillanatban a fonalat feszítő erő gyorsítja az éppen álló, de felfelé induló szélső testeket. Mekkora ez a gyorsulás? Tegyük fel, hogy a bal oldali csigától a középső testhez vezető

A P

fonál

Δ t

idő alatt már egy kicsiny

Δ α

szöggel túllendült a vízszintes helyzeten (3. ábra). Jelöljük a szélső testek sebességét

Δ v

-vel! Ez a sebesség (a fonal nyújthatatlansága miatt) megegyezik a

P

pontban levő középső test sebességének

A P

irányú vetületével, vagyis

\begin{matrix} \frac{Δ v}{v} = sin Δ α \approx Δ α . \end{matrix}

Másrészt a

P Q A

derékszögű háromszögből

\begin{matrix} \frac{v Δ t}{h} = tg Δ α \approx Δ α . \end{matrix}

A fenti két egyenlet összevetéséből

\begin{matrix} Δ v = \frac{v^{2}}{h} Δ t, \end{matrix}

vagyis a szélső testek gyorsulására

\begin{matrix} a = \frac{Δ v}{Δ t} = \frac{v^{2}}{h} \end{matrix}

adódik.

Ugyanehhez a képlethez úgy is eljuthatunk, ha felírjuk, hogy a vízszinteshez közeli

A P

szakasz hossza időben hogyan változik. Mivel

P Q \approx v t

(ahol

t

a 2.

(b)

ábrán látható állapottól mért idő), Pitagorasz tétele szerint

\begin{matrix} A P = \sqrt[]{h^{2} + v^{2} t^{2}} = h \sqrt[]{1 + \frac{v^{2} t^{2}}{h^{2}}} \approx h + \frac{v^{2} t^{2}}{2 h} = h + \frac{a}{2} t^{2} . \end{matrix}

Ebből leolvashatjuk, hogy az

A P

szakasz hossza

a = v^{2} / h

gyorsulással növekszik, s a fonal nyújthatatlansága miatt a bal oldali test is ugyanekkora nagyságú, függőlegesen felfelé irányuló gyorsulással kell rendelkezzék.

A fonal által kifejtett erő a szélső testek mozgásegyenletéből kapható meg:

\begin{matrix} F_{fonal} - M g = M \frac{v^{2}}{h}, \end{matrix}

azaz

\begin{matrix} F_{fonal} = M g [1 + 2 (2 - \sqrt[]{3})] = 1, 536 M g \approx 15 N. \end{matrix}

Így már érthető, miért nem szakad el ebben a helyzetben a ,,néhányszor 10 N terhelést kibíró'' fonal.
Érdemes felfigyelni arra, hogy a szélső testek kétszer is emelkednek és kétszer is süllyednek egy-egy periódus során, hiszen a 2. ábrán feltüntetett mindhárom állapotban éppen állnak. Süllyedésük az idő függvényében nagyjából a 4. ábrán vázolt módon történik.

4. ábra

2. Egy átlátszatlan lapon kicsiny lyukak vannak az 5. ábrán látható ,,háromszög-rács'' elrendezésben. A lapot monokromatikus,

λ

hullámhosszúságú lézerfénnyel világítjuk meg merőlegesen. A rácsállandó

d = 100 λ

5. ábra

Ábrázoljuk vázlatosan (a méretek, valamint a vízszintes és a függőleges irányok bejelölésével), hogy milyen elhajlási képet figyelhetünk meg a rácstól 3 m távolságra elhelyezett ernyőn!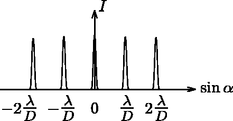

Megoldás. Elevenítsük fel azokat az ismereteket, amelyek a síkbeli optikai rácson (párhuzamos, egymástól egyenlő távolságra lévő rések rendszerén) áthaladó monokromatikus fény diffrakciójára vonatkoznak! Világítsuk meg az optikai rácsot a síkjára merőleges, keskeny lézersugárral. A ráccsal párhuzamosan elhelyezett ernyőn ekkor közelítőleg egyenlő távolságra elhelyezkedő fényes foltokat látunk. Jelöljük

D

-vel a rácsállandót,

λ

-val a hullámhosszat. Az intenzitás menetét az elhajlási (diffrakciós) szög szinuszának függvényében a 6. ábra mutatja.

6. ábra

Az ábrán látható intenzitáseloszlást jól alátámasztja az a középiskolában tanult közelítés, amely szerint a rács rései olyan keskenyek, hogy egy-egy résen belül, az onnan kiinduló elemi hullámok azonos fázisban vannak (Huygens‐Fresnel-elv). Ugyanakkor két egymás melletti résből induló elemi hullámok erősítésének feltétele:

\begin{matrix} D sin α_{k} = k λ (k = 0, \pm 1, \pm 2, ...) . \end{matrix}

7. ábra

Ha az ernyő

S

távolságra van az optikai rácstól (7. ábra), akkor az első főmaximum távolsága a centrumtól

\begin{matrix} s_{1} \approx S \cdot sin α_{1} = S \frac{λ}{D}, \end{matrix}

és általában, a

k

-adik főmaximum távolsága

\begin{matrix} s_{k} \approx k S \frac{λ}{D} . \end{matrix}

(Itt kihasználtuk, hogy

λ ≪ d

miatt

α_{k} ≪ 1

, és így

sin α_{k} \approx α_{k}

.)
Térjünk rá a feladatban szereplő háromszögrácsra! Mivel a háromszögrács síkjára merőlegesen érkezik a fény, ezért minden egyes lyukból azonos fázisú elemi hullámok indulnak ki. Ezek a rácsra merőleges irányban tovább haladva biztosan erősítik egymást, útkülönbség nélkül,

α = 0

irányban jelölik ki a keletkező diffrakciós kép centrumát az elég távol lévő ernyőn.
Hol lesz ehhez a centrumhoz legközelebb újra egy erősítési hely az ernyőn? Milyen irányban?
Válasszuk ki valamelyik kicsiny lyukat. Gondolatban húzzunk ezen a lyukon át egy olyan egyenest, amelyik átmegy valamelyik, hozzá legközelebb eső lyukon. Ez az egyenes még egy sorozat lyukon fog áthaladni, amelyek mind

d

távolságra követik egymást. Most keressünk egy másik lyuksort, amelyen átmenő egyenes párhuzamos az előzővel. Sok ilyen lyuksort találunk, ezek egymástól

D = d \frac{\sqrt[]{3}}{2}

távolságra helyezkednek el (8. ábra). Figyeljük meg azt az irányt a térben, amely az elképzelt egyenesekre merőleges, de a már kijelölt centrum felé vezető iránnyal akkora

α_{1}

szöget zár be, hogy teljesül a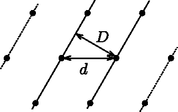

\begin{matrix} D sin α_{1} = λ \end{matrix}

összefüggés.

8. ábra

Ha az ilyen irányba haladó elemi hullámok eredőjét vizsgáljuk a messze lévő ernyőn, akkor azt látjuk, hogy a kiválasztott egyenesen elhelyezkedő lyukakból jövő elemi hullámok erősítik egymást, mert az ernyőhőz érve már szinte nincs is útkülönbség köztük. De a szomszédos egyenesen fekvő lyuksorból induló elemi hullámokkal is erősíteni fogják egymást, mert köztük az útkülönbség (

D sin α_{1}

) éppen

λ

-val egyenlő, és ugyanez igaz a többi egyenesen fekvő lyukakból induló hullámokra is. Tehát ebben az irányban az összes lyukon átjövő fény erősíteni fogja egymást!
Így az ernyőn a centrumhoz legközelebbi (egyik) erősítési helynek a centrumtól való távolsága:

\begin{matrix} s_{1} = S \frac{λ}{D} = \frac{2}{\sqrt[]{3}} S \frac{λ}{d} = 2 \sqrt[]{3} cm \approx 3, 4 cm . \end{matrix}

Hat ilyen pont lesz az ernyőn, amelyek egy ‐ a centrum körüli ‐ szabályos hatszög csúcsait jelölik ki. Ez azért van így, mert három, egymással 120‐

120^{\circ}

-os szöget bezáró egyenes-sereget (lyuksor-sereget) jelölhetünk ki a háromszögrácson.
Azt is észrevehetjük, hogy olyan helyen is lesz az ernyőn erősítés, melynek távolsága a centrumtól

2 s_{1},3 s_{1}, ...,

hiszen ekkor az egymás melletti lyuksorokból érkező hullámok

2 λ,3 λ, ...

útkülönbséggel találkoznak az ernyőn. Ezek szerint a rácson felvett mindegyik egyenes-sereg az ernyőn egy pontsorozatot eredményez. Ha a rácson elképzelt lyuksorok pl. vízszintes egyenesek mentén helyezkednek el, akkor az ernyőn keletkező pontsorozat egy függőleges egyenesre illeszkedik.
Hatágú ,,csillag'' lesz tehát a kép? Nem egészen, bár ezek a most elképzelt pontok mind megjelennek az ernyőn, de nem csak ezek jelennek meg! Képzeljük el például a háromszögrácson azt az egyenes- (lyuksor)-sereget, amelyet a 9. ábra bal oldalán látunk.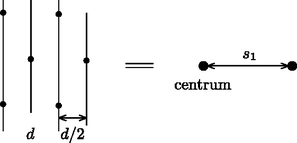

9. ábra

Ez egy

\frac{d}{2}

rácsállandójú optikai rácsnak felel meg, ezért az ernyőn a megfelelő erősítési helyek

\begin{matrix} s_{1}' = S \frac{λ}{\frac{d}{2}} = 6 cm \end{matrix}

távolságra követik egymást. Most is igaz, hogy minél sűrűbb optikai rácsba rendeződve képzeljük el a lyukakat, annál messzebb kerülnek egymástól a megfelelő erősítési helyek az ernyőn.
Meg lehet mutatni, hogy a háromszögrács ,,képe'' az ernyőn ugyancsak szabályos háromszögrács lesz, mert kölcsönösen egyértelműen egymáshoz rendelhető a lyukakra illeszthető egyenessereg és az ernyőn megjelenő, interferencia eredményezte ponthalmaz. (Ennek belátásához legközelebb Varjas Dániel jutott el, aki díjnyertes dolgozatában a különböző módon felvehető elemi cellák területének egyenlőségét használta ki.) Mégis lesz valami eltérés a lyukak alkotta háromszögrács és a diffrakciós pontok alkotta háromszögrács között (a pontok távolságában mutatkozó eltérésen kívül is): az egyik pontrács

90^{\circ}

-os elforgatottja a másiknak. (Most akár

30^{\circ}

-os elforgatottat is mondhatnánk, de egy téglalaprács esetén nagyon jól látszik, hogy

90^{\circ}

-os elforgatásról van szó.)
Mindezt a 10. ábra szemlélteti, melynek alsó részén a lyukak rácsa, felül pedig az ernyőn látható elhajlási kép látható, természetesen eltérő méretarányban.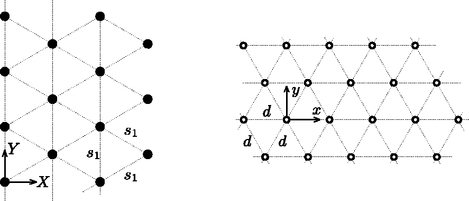

10. ábra

A feladatban szereplő háromszögrácsot úgy is előállíthatjuk, hogy három, egyenként

D

állandójú, közönséges optikai rácsot egymásra fektetünk. A feltétel csak annyi, hogy mindegyik rács rései a másik rács réseivel

60^{\circ}

-os szöget zárjanak be. Az így keletkező lyukak ugyan nem kör, hanem hatszög alakúak lesznek, de ha a rések szélessége sokkal kisebb a rácsállandónál, akkor ennek nincs jelentősége. Sőt! Ha elhagyjuk a harmadik rácsot, és csupán két, egymással

60^{\circ}

-os szöget bezáró rács diffrakciós képét vizsgáljuk, ez is ugyanaz lesz, mint az előbbiek. Ebben az esetben ugyanis a lyukak ugyan rombusz alakúak, de ugyanabban a szabályos háromszögrácsban rendeződnek el, tehát jó közelítésben ugyanazt a diffrakciós képet eredményezik. Az eredményhirdetéskor Komlósi István egyetemi hallgató mutatta be ezt a kísérletet.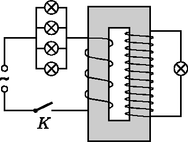

3. Egy jó minőségű transzformátor szekunder tekercsének menetszáma háromszorosa a primer tekercsének. Ezt a trafót a 11. ábra szerint hálózati váltóáramú feszültségforrásra kapcsoljuk a következő módon: A primer körbe egymással párhuzamosan iktatunk be öt egyforma, a hálózati feszültségre méretezett izzó közül négyet, az ötödiket a szekunder körbe kötjük. Mi történik a

K

kapcsoló zárása után?

11. ábra

a)

Mindegyik izzó tűrhetően ég.

b)

A primer körbeli négy izzó szépen ég, az ötödik legfeljebb pislákol.

c)

A szekunder körbeli izzó egy pillanat alatt kiég, utána a primer körbeli izzók sem világítanak, mivel a primer tekercs fojtótekercsként hat.
Melyik a helyes válasz?

Megoldás. Ezt a feladatot is többféleképpen lehet megoldani. Eljuthatunk a helyes válaszhoz okoskodással, analógiák felhasználásával, úgy, ahogy például az előző feladat megoldásának bemutatásakor jártunk el. Most más utat választunk: bemutatjuk a lehető legrövidebb utat, ahogy a megoldást megkaphatjuk.
Ismert ‐ szakkönyvekben, példatárakban megtalálható, így az Eötvös-versenyen szabadon felhasználható ‐ a transzformátor helyettesítő kapcsolása, ami a 12. ábrán látható.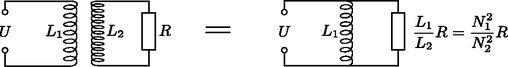

12. ábra

Első közelítésben tekintsünk el attól, hogy az izzók ellenállása függ a rajtuk áthaladó áramtól (erre még visszatérünk), és induljunk ki abból, hogy van öt egyforma ellenállásunk. Az eredő a szekunder oldalon

R

, primer oldalon

R / 4

, a párhuzamos kapcsolás miatt. Mivel a szekunder tekercs menetszáma háromszorosa a primer tekercsének, ezért a helyettesítő kapcsolásban ide

R / 9

ellenállás kerül (13. ábra).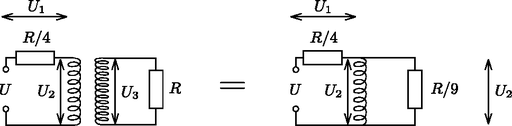

13. ábra

Egy jó minőségű transzformátor szekunder tekercsének váltóáramú ellenállása sokkal nagyobb, mint az izzó ellenállásának kilenced része, ezért jó közelítésben írhatjuk:

\begin{matrix} U_{1} : U_{2} = \frac{R}{4} : \frac{R}{9}, \end{matrix}

valamint

U_{1} + U_{2} = U

és

U_{3} = 3 U_{2}

. Ezekből az összefüggésekből következik:

\begin{matrix} U_{1} = \frac{9}{13} U, U_{2} = \frac{4}{13} U, U_{3} = \frac{12}{13} U . \end{matrix}

A primer tagban egy-egy izzóra jutó teljesítmény:

\begin{matrix} \frac{U_{1}^{2}}{R} = \frac{81}{169} \frac{U^{2}}{R} = 0, 48 \frac{U^{2}}{R}, \end{matrix}

durván fele annak a teljesítménynek, amellyel a hálózati feszültségen világítanának. A szekunder körben az izzó teljesítménye:

\begin{matrix} \frac{U_{3}^{2}}{R} = \frac{144}{169} \frac{U^{2}}{R} = 0, 85 \frac{U^{2}}{R}, \end{matrix}

nincs nagyon messze attól a teljesítménytől, amellyel ez az izzó a hálózati feszültségen világítana.
Ha most figyelembe vesszük azt a tényt, hogy alacsonyabb feszültségen (tehát alacsonyabb hőmérsékleten) az izzó ellenállása is kisebb, azt mondhatjuk, hogy a primer ágban levő izzók ténylegesen nagyobb teljesítménnyel világítanak, mint amit most kiszámítottunk.
Bátran állíthatjuk, hogy mindegyik izzó tűrhetően ég, vagyis az

a)

válasz a helyes.

Azok számára, akik járatosak a szinuszos váltóáramú hálózatok komplex számokat felhasználó számításaiban, megmutatjuk a 12. ábrán látható két kapcsolás egyenértékűségét, melyet a megoldásban felhasználtunk. A transzformátor primer és szekunder körére felírhatjuk:

\begin{matrix} \tilde{U} & = j ω L_{1} \tilde{I_{1}} + j ω M \tilde{I_{2}}, \\ 0 & = j ω M \tilde{I_{1}} + j ω L_{2} \tilde{I_{2}} + R \tilde{I_{2}}, \end{matrix}

ahol

\tilde{I_{1}}

a primer-,

\tilde{I_{2}}

a szekunder körben folyó áram komplex alakja,

M

pedig a két tekercs kölcsönös indukciós együtthatója. A második egyenletből

\tilde{I_{2}}

-t kifejezve és az első egyenletbe helyettesítve, valamint felhasználva a szoros csatolás esetén érvényes

M^{2} = L_{1} L_{2}

összefüggést, rendezés után kapjuk:

\begin{matrix} \tilde{U} = \frac{j ω L_{1} R}{j ω L_{2} + R} \tilde{I_{1}} = \tilde{Z} \cdot \tilde{I_{1}} . \end{matrix}

A helyettesítő kapcsolásban

j ω L_{1}

és

R \frac{L_{1}}{L_{2}}

váltóáramú ellenállások párhuzamos eredőjét kell kiszámítanunk:

\begin{matrix} \tilde{Z'} = \frac{j ω L_{1} \cdot R \frac{L_{1}}{L_{2}}}{j ω L_{1} + R \frac{L_{1}}{L_{2}}} = \frac{j ω L_{1} R}{j ω L_{2} + R} = \tilde{Z} . \end{matrix}

Éppen ez az, amit be akartunk bizonyítani.

A verseny eredménye

A verseny ünnepélyes eredményhirdetésére és a díjkiosztásra 2005. november 25-én délután került sor az ELTE Mogyoródi József termében.
Bevezetésként a versenybizottság elnöke emlékezett vissza az 50 évvel ezelőtti és a 25 évvel ezelőtti versenyre. Írásvetítőn kivetítette az 50 évvel korábbi feladatokat, valamint az akkori nyertesek egy-egy KöMaL feladatra adott egykori megoldását. A feladatokat Kárteszi Ferenc, illetve Prékopa András tűzte ki (akkor még nem volt fizika rovat a KöMaL-ban). Aki a versenyt megnyerte, Bártfai Pál matematikus, ma a Kürschák-verseny zsűrijének oszlopos tagja. Elfogadta meghívásunkat, személyesen (családosan!) megjelent az eredményhirdetésen, és néhány mondatban felelevenítette emlékeit. Nem csak a versenyről beszélt, hanem a felkészülésről is, Vermes tanár úr szakköréről, melynek oly sokat köszönhetett fizikából. Utána az elnök az 50 évvel ezelőtti második helyezett, az Egyesült Államokban élő Gutai László fizikus levelét olvasta fel. Ő is megemlékezett egykori tanáráról, Varga Zoltánról, aki őt Újpesten tanította. A 25 évvel ezelőtti Eötvös-verseny nyertesek közül Szalontai Zoltán és Umann Gábor jelent meg, mindketten a KöMaL szorgalmas feladatmegoldói voltak, négy éven át jelent meg fényképük a legjobb megoldók között. Ezeket a képeket egymás mellé vetítve láthatták most a megjelentek.
Ezek után került sor a feladatok fent leírt megoldásának ismertetésére. Mindegyik feladathoz kapcsolódott kísérlet is: az elsőt Honyek Gyula, a másodikat és a harmadikat Gnädig Péter mutatta be.
Következtek az ünnepélyes eredményhirdetés legizgalmasabb pillanatai: az elnök Patkós András akadémikust, az Eötvös Loránd Fizikai Társulat elnökét kérte fel a díjak és az oklevelek átadására.
I. díjat, a vele járó Eötvös-verseny érmet és 20 ezer forintos jutalmat kapta Varjas Dániel, a BME mérnök-fizikus hallgatója, aki a dunaújvárosi Széchenyi István Gimnáziumban érettségizett mint Kispál István tanítványa. Varjas Dániel tavaly is első díjat kapott az Eötvös-versenyen, így hát ő az első az országban, aki két Eötvös-verseny éremmel is rendelkezik. Nehéz volt megmondani, hogy ő, vagy Kispál tanár úr hatódott-e meg jobban, amikor kiderült, hogy Dani nyert a versenyen.
A versenybizottság döntése értelmében hárman kaptak II. díjat és vele 14 ezer forint jutalmat, ketten III. díjat és vele 12 ezer forint jutalmat, valamint hat versenyzőt részesített a zsűri dicséretben:
II. díjasok: Halász Gábor, az ELTE Radnóti Miklós Gyakorló Gimnáziumának 12. osztályos tanulója, Honyek Gyula tanítványa; Kómár Péter, az ELTE fizikus hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett mint Dvorák Cecília tanítványa és Szolnoki Lénárd, a Debreceni Református Kollégium Dóczy Gimnáziumának 10. osztályos tanulója, Tófalusi Péter tanítványa.
III. díjasok: Kónya Gábor, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 11. osztályos tanulója, Horváth Gábor tanítványa és Széchenyi Gábor, a szolnoki Verseghy Ferenc Gimnázium 12. osztályos tanulója, Pécsi István tanítványa.
Dicséretet kapott Farkas Ádám László, a miskolci Földes Ferenc Gimnázium 11. osztályos tanulója, Zámborszky Ferenc tanítványa; Ferenczy Máté, a BME mérnök-fizikus hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett mint Dvorák Cecília tanítványa; Németh Balázs, a székesfehérvári Tóparti Gimnázium 11. osztályos tanulója, Tóthné Rohovszky Katalin tanítványa; Pálinkás András, az ELTE fizikus hallgatója, aki a budapesti Piarista Gimnáziumban érettségizett mint Futó Béla tanítványa; Paulin Roland, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 12. osztályos tanulója, Horváth Gábor tanítványa és Végh Sándor, a Debreceni Egyetem Kossuth Lajos Gimnáziumának 12. osztályos tanulója, Kirsch Éva és

\begin{matrix} Szegedi Ervin \end{matrix}

tanítványa.
A nyertes versenyzők tanárai, akik szintén meghívót kaptak az ünnepélyes díjkiosztásra, a Typotex Kiadó által erre a célra felajánlott könyvek közül válogathattak.
Végül Patkós András akadémikus elevenítette fel az Eötvös-versennyel kapcsolatos régebbi és legújabb emlékeit, benyomásait (lásd a hátsó belső borítón középen jobbra). Utána közös fényképezkedés következett, melyen az 50 és a 25 évvel ezelőtti nyertes fogta közre az idei első díjast, s egy jó hangulatú baráti beszélgetésben folytatódott az egymást eddig java részt csak hírből ismerő meghívottak társalgása. A Ramasoft Rt. jóvoltából üdítő és finom szendvicsek is jutottak a végig ott maradóknak.