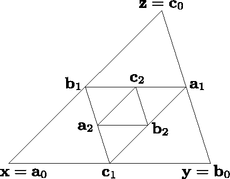Kezdőlap


Cím:	Számtani közép, mértani közép, meg ilyenek
Szerző(k):	Kovács Veronika , Petz Dénes
Füzet:	2006/március, 130 - 136. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Több, mint kétezer évvel ezelőtt a régi görögök arányokra alapozva már használták a számtani, a mértani és a harmonikus közép fogalmát. Legyen $x$ és $y$ pozitív szám, a számtani közepük:

\begin{matrix} A (x, y) : = \frac{x + y}{2}, \end{matrix}

a mértani közepük:

\begin{matrix} G (x, y) : = \sqrt[]{x y} \end{matrix}

és harmonikus közepük:

\begin{matrix} H (x, y) : = \frac{2}{\frac{1}{x} + \frac{1}{y}} = \frac{2 x y}{x + y} . \end{matrix}

Mind a három mennyiség

x

és

y

közé esik, ez indokolja a közép elnevezést. Ha

x < m < y

, akkor a számtani közepet az

\begin{matrix} y - m = m - x, \end{matrix}

a mértani közepet az

\begin{matrix} \frac{m}{x} = \frac{y}{m} vagy \frac{y - m}{m - x} = \sqrt[]{\frac{y}{x}}, \end{matrix}

végül a harmonikus közepet a kicsit bonyolultabb

\begin{matrix} y = m + \frac{y}{n} és m = x + \frac{x}{n} \end{matrix}

tulajdonságok jellemzik. Ha ebből az egyenletrendszerből

n

-et kiküszöböljük, akkor egy egyszerűbb alakot kapunk:

\begin{matrix} \frac{y - m}{m - x} = \frac{y}{x} . \end{matrix}

A régi görögök a kocka geometriai harmóniáját látták abban a tényben, hogy az élek számának és a lapok számának harmonikus közepe éppen a csúcsok száma.
Az

x

A (x, y)

H (x, y)

és

y

számok arányai közötti

\begin{matrix} x : A (x, y) = H (x, y) : y \end{matrix}

összefüggést már a babiloniaiak is ismerték, de feledésbe ment, Pitagorasz újra felfedezte. Az említett közepeket egyébként pitagoraszi közepeknek is szokták nevezni.

A számtani és mértani közép közötti egyenlőtlenség

A számtani és mértani közép közötti egyenlőtlenségre egy algebrai és egy geometriai bizonyítást adunk. A

\begin{matrix} \sqrt[]{x y} \leq \frac{x + y}{2} \end{matrix}

(1)

egyenlőtlenség ekvivalens a

\begin{matrix} 4 x y \leq {(x + y)}^{2} \end{matrix}

egyenlőtlenséggel, ami nem más, mint

\begin{matrix} 0 \leq {(x - y)}^{2} . \end{matrix}

Ez mindig igaz, és az egyenlőség akkor és csak akkor áll fenn, ha

x = y

. Ezzel az (1) egyenlőtlenséget bebizonyítottuk, sőt szükséges és elégséges feltételt is kaptunk az egyenlőségre.
A geometriai bizonyítás a derékszögű háromszögre vonatkozó magasságtételen alapszik.

A magasságtétel szerint

m = \sqrt[]{x y}

, ahol

x

és

y

az átfogó szeletei. A háromszög köré írt kör

r

sugara

x

és

y

számtani közepe. Az ábrából látszik, hogy

m \leq r

, és ez a számtani és mértani közép közötti egyenlőtlenség

A harmonikus és a mértani közép közötti

\begin{matrix} H (x, y) \leq G (x, y) \end{matrix}

egyenlőtlenség egyszerű számolással visszavezethető a számtani és mértani közép közötti egyenlőtlenségre.
Most az (1) egyenlőtlenség többváltozós alakját kívánjuk igazolni. Legyenek

x_{1}

x_{2}

x_{3}

és

x_{4}

pozitív számok. Az (1) egyenlőtlenség kétszeri alkalmazásával kapjuk, hogy

\begin{matrix} \sqrt[]{(x_{1} x_{2})} \sqrt[]{(x_{3} x_{4})} \leq (\frac{x_{1} + x_{2}}{2}) (\frac{x_{3} + x_{4}}{2}) . \end{matrix}

A jobb oldalon álló szorzatra megint alkalmazzuk a számtani és mértani közép közötti egyenlőtlenséget:

\begin{matrix} (\frac{x_{1} + x_{2}}{2}) \cdot (\frac{x_{3} + x_{4}}{2}) \leq {(\frac{\frac{x_{1} + x_{2}}{2} + \frac{x_{3} + x_{4}}{2}}{2})}^{2} . \end{matrix}

A két egyenlőtlenséget összevetve és négyzetgyököt vonva az adódik, hogy

\begin{matrix} \sqrt[4]{x_{1} x_{2} x_{3} x_{4}} \leq \frac{x_{1} + x_{2} + x_{3} + x_{4}}{4} . \end{matrix}

Ez a számtani és mértani közép közötti egyenlőtlenség négyváltozós alakja. Ugyanezt az eljárást ismételve juthatunk el az

\begin{matrix} \sqrt[n]{x_{1} x_{2} ... x_{n}} \leq \frac{x_{1} + x_{2} + ... + x_{n}}{n}, \end{matrix}

(2)

egyenlőtlenséghez, ahol

n = 2^{k}

. Ha az

x_{i}

-k között

v

darab

x

és

n - v

darab

y

van, akkor egyenlőtlenségünk az

\begin{matrix} \sqrt[n]{x^{v} y^{n - v}} = x^{\frac{v}{n}} y^{\frac{n - v}{n}} \leq \frac{v x + (n - v) y}{n} = \frac{v}{n} x + \frac{n - v}{n} y \end{matrix}

formát ölti. Ez áttekinthetőbb, ha

\frac{v}{n}

helyébe

α

-t írunk:

\begin{matrix} x^{α} y^{1 - α} \leq α x + (1 - α) y . \end{matrix}

(3)

Így a súlyozott számtani-mértani közép egyenlőtlenséghez jutottunk, ami

α = \frac{1}{2}

esetén adja vissza (1)-t. Bizonyításunkban

α

nem lehet egyelőre tetszőleges

(0; 1)

-beli szám, csupán

\frac{v}{2^{k}}

alakú. (Az ilyen számokat néha diadikus racionálisaknak nevezik.)

\frac{v}{2^{k}}

alakú számokkal bármilyen

α \in (0,1)

közelíthető, ezért a (3) egyenlőtlenség minden 0 és 1 közé eső

α

-ra igaz.
A gondolatmenetet egy kicsit továbbfejlesztve eljuthatunk az

\begin{matrix} x_{1}^{α_{1}} x_{2}^{α_{2}} ... x_{m}^{α_{m}} \leq α_{1} x_{1} + α_{2} x_{2} + ... + α_{m} x_{m} \end{matrix}

(4)

egyenlőtlenséghez, ami akkor igaz, ha az

α_{1}, α_{2}, ..., α_{m}

pozitív számokra

α_{1} + α_{2} + ... + α_{m} = 1

teljesül. (4) a súlyozott számtani-mértani közép egyenlőtlenség általános alakja.
A súlyozott számtani közép előfordul például a következő helyzetben: Tegyük fel, hogy egy diáknak van két darab 5-ös dolgozata és egy 1-es és egy 2-es felelete. Úgy akarjuk kiszámítani az átlagát, hogy a dolgozatai kétszer olyan súllyal számítanak, mint a feleletei. Ekkor az átlag:

\begin{matrix} \frac{(5 + 5) + (5 + 5) + 1 + 2}{6} = \frac{2}{6} \cdot 5 + \frac{2}{6} \cdot 5 + \frac{1}{6} \cdot 1 + \frac{1}{6} \cdot 2 = 3, 8 \dot{3} . \end{matrix}

Ha az egyszerű átlagot számoljuk, akkor

3,25

kerekítve

3

-as. De ha figyelembe vesszük a dolgozatok nagyobb súlyát, akkor a diák a

4

-est is megérdemli.

A logaritmikus közép

x

és

y

pozitív számok logaritmikus közepe:

\begin{matrix} L (x, y) : = {\begin{matrix} \frac{x - y}{ln x - ln y}, & ha x \neq y, \\ x, & ha x = y . \end{matrix} \end{matrix}

(5)

Ez a képlet jóval bonyolultabb, mint a számtani, vagy a mértani közép. Az sem látszik azonnal, hogy

L (x, y)

egy pozitív szám, még kevésbé az, hogy

x

és

y

közé esik. Mindezek a tulajdonságok igazak és következnek az alábbi tételből.

1. tétel.

\begin{matrix} G (x, y) \leq L (x, y) \leq A (x, y) \end{matrix}

minden pozitív

x

és

y

számra.

Bizonyítás. Osszuk el a

\begin{matrix} \sqrt[]{x y} \leq \frac{x - y}{ln x - ln y} \leq \frac{x + y}{2} \end{matrix}

igazolandó egyenlőtlenséget

y

-nal, így azt kapjuk, hogy

\begin{matrix} \sqrt[]{\frac{x}{y}} \leq \frac{\frac{x}{y} - 1}{ln \frac{x}{y}} \leq \frac{1}{2} (\frac{x}{y} + 1) . \end{matrix}

Látjuk, hogy mindenütt

x

-nek és

y

-nak a hányadosa szerepel, ezért érdemes ennek helyébe egy új változót írni, mondjuk

z^{2}

-et:

\begin{matrix} z \leq \frac{z^{2} - 1}{2 ln z} \leq \frac{1}{2} (z^{2} + 1) . \end{matrix}

Tehát a következő két egyenlőtlenséget kell igazolnunk:

\begin{matrix} 2 z \leq \frac{z^{2} - 1}{ln z} \end{matrix}

(6)

és

\begin{matrix} \frac{z^{2} - 1}{ln z} \leq z^{2} + 1. \end{matrix}

(7)

Az egyszerűség kedvéért mindkét egyenlőtlenséget a

z > 1

esetben igazoljuk (ekkor

ln z > 0

), a

0 < z < 1

eset teljesen hasonlóan tárgyalható. Így (7) a

\begin{matrix} \frac{z^{2} - 1}{z^{2} + 1} \leq ln z \end{matrix}

alakot ölti.

z = 1

esetén mindkét oldal

0

. Az egyenlőtlenség biztosan fennáll, ha a bal oldal lassabban növekszik, mint a jobb, vagyis a bal oldal deriváltja kisebb, mint a jobb oldalé. Elvégezzük a deriválást. Meg kell mutatnunk, hogy

\begin{matrix} \frac{2 z (z^{2} + 1) - (z^{2} - 1) 2 z}{{(z^{2} + 1)}^{2}} \leq \frac{1}{z}, \end{matrix}

amit átrendezve

\begin{matrix} 0 \leq z^{4} - 2 z^{2} + 1 = {(z^{2} - 1)}^{2} \end{matrix}

adódik. Természetesen ez igaz, így (7) bizonyítását elvégeztük.
A (6) egyenlőtlenséget a

\begin{matrix} 2 ln z \leq \frac{z^{2} - 1}{z} \end{matrix}

(8)

formára hozzuk.

z = 1

esetén mindkét oldal 0. Hasonlóan, mint az előző esetben, megmutatjuk, hogy a bal oldal deriváltja kisebb, mint a jobb oldalé. Most a következő egyenlőtlenséget kell bizonyítanunk:

\begin{matrix} \frac{2}{z} \leq \frac{2 z \cdot z - (z^{2} - 1) \cdot 1}{z^{2}}, \end{matrix}

ami átrendezés után

\begin{matrix} 2 \leq z + \frac{1}{z}, \end{matrix}

és tovább alakítva

\begin{matrix} 0 \leq {(z - 1)}^{2} . \end{matrix}

Ez nyilvánvaló, és ezzel a (6) egyenlőtlenség bizonyítását befejeztük.
Ha tudunk integrálni, akkor az

\begin{matrix} x^{α} y^{1 - α} \leq α x + (1 - α) y \end{matrix}

egyenlőtlenségeket integrálva

α

szerint

0

-tól

1

-ig, éppen az

L (x, y) \leq A (x, y)

egyenlőtlenséghez jutunk. Ebből azt is megjegyezhetjük, hogy a logaritmikus közép a súlyozott mértani közepeknek a súlyok szerint vett integrálja. (A számtani közép pedig a súlyozott számtani közepek hasonló integrálja.)

Vektorok számtani közepe

Legyenek

x_{1}, x_{2}, ..., x_{n}

a sík vektorai. Számtani közepük

\begin{matrix} A (x_{1}, x_{2}, ..., x_{n}) = \frac{1}{n} (x_{1} + x_{2} + ... + x_{n}) . \end{matrix}

Az egyszerűség kedvéért foglalkozzunk az

n = 3

esettel. Ekkor a három vektort inkább az

x, y

és

z

betűkkel jelöljük. Ha

x = (x_{1}, x_{2})

y = (y_{1}, y_{2})

és

z = (z_{1}, z_{2})

, akkor

\begin{matrix} A (x, y, z) = (\frac{1}{3} (x_{1} + y_{1} + z_{1}), \frac{1}{3} (x_{2} + y_{2} + z_{2})) . \end{matrix}

x

y

és

z

vektorok számtani közepe nem más, mint a három pont által meghatározott háromszög súlypontjába mutató vektor. A számtani középnek tehát egyszerű geometriai jelentése van

2. tétel. Legyen

x

y

és

z

három vektor a síkon. Ekkor a sík helyvektorain értelmezett

\begin{matrix} w \mapsto {| w - x |}^{2} + {| w - y |}^{2} + {| w - z |}^{2} \end{matrix}

függvény minimumhelye a három vektor számtani közepe. (Itt az abszolútértékjel a vektorok hosszát jelöli.)

Bizonyítás. Jelölje

m

x

y

és

z

vektorok számtani közepét,

\begin{matrix} m : = \frac{x + y + z}{3} . \end{matrix}

A következő azonosság maga a bizonyítás:

\begin{matrix} {| w - x |}^{2} + {| w - y |}^{2} + {| w - z |}^{2} = \\ = 3 {| w - m |}^{2} + {| x |^{2} + | y |}^{2} + {| z |}^{2} - \frac{1}{3} {| x + y + z |}^{2} . \end{matrix}

Tételezzük fel, hogy van egy gépünk, ami két vektornak megadja a számtani közepét. Lehetne-e ezt a gépet három vektor számtani közepének meghatározására használni? Közvetlen módon talán nem, de építhetnénk belőle egy új berendezést, amely három bemenő vektorból három kimenő vektort ad meg. Ha

x

y

és

z

a bemenő vektorok, akkor a kimenők

\begin{matrix} x' : = \frac{1}{2} (y + z), y' : = \frac{1}{2} (z + x), z' : = \frac{1}{2} (x + y) . \end{matrix}

Új berendezésünk azt a gépet használja, amely két vektornak képes megadni a számtani közepét. Ezt a berendezést használjuk ismételten, az általa kiadott vektorokat tápláljuk be újra és újra. Így a következő rekurziót végeztetjük.
Legyen az

(a_{0}, b_{0}, c_{0})

vektorhármas a kiindulási

(x, y, z)

hármas. Ha az

(a_{n}, b_{n}, c_{n})

hármas már megvan, akkor a berendezésnek beadva, az kiadja az

(a_{n + 1}, b_{n + 1}, c_{n + 1})

hármast, az

\begin{matrix} a_{n + 1} : = \frac{1}{2} (b_{n} + c_{n}), b_{n + 1} : = \frac{1}{2} (c_{n} + a_{n}), c_{n + 1} : = \frac{1}{2} (a_{n} + b_{n}) \end{matrix}

képletek szerint. Amint

n

növekszik, az

(a_{n}, b_{n}, c_{n})

vektorhármasok egyre kisebb

Δ_{n}

háromszögeket határoznak meg, és egyre jobban megközelítik a kezdetben adott három vektor számtani közepét, amely

Δ_{0}

súlypontja. Valójában a

Δ_{0}, Δ_{1}, Δ_{2}, ...

háromszögek súlypontjai egybeesnek, hiszen a rekurzióból adódóan

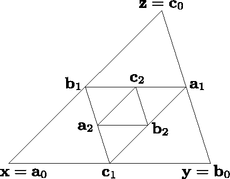\begin{matrix} \frac{1}{3} (a_{n + 1} + b_{n + 1} + c_{n + 1}) = \frac{1}{3} (\frac{1}{2} (b_{n} + c_{n}) + \frac{1}{2} (c_{n} + a_{n}) + \frac{1}{2} (a_{n} + b_{n})) = \\ = \frac{1}{3} (a_{n} + b_{n} + c_{n}) . \end{matrix}

A rekurzióval értelmezett

(a_{n}, b_{n}, c_{n})

vektorhármasok által meghatározott háromszögek egyre kisebbek, és megközelítik az

a_{0}

b_{0}

és

c_{0}

vektorok számtani közepét, a súlypontot

Befejezésül megemlítjük, hogy ha az

\begin{matrix} a_{n + 1} : = M (b_{n}, c_{n}), b_{n + 1} : = M (c_{n}, a_{n}), c_{n + 1} : = M (a_{n}, b_{n}) \end{matrix}

rekurziót egy

a_{1}

b_{1}

c_{1}

számhármasból indítjuk

M

helyében a geometriai középpel, akkor a határérték az adott számhármas geometriai közepe (hasonlóan a fent részletezett számtani közép esetéhez). Ha

M

helyébe a logaritmikus közepet tesszük, akkor

a_{n}

b_{n}

és

c_{n}

közös határétéke létezik, és méltán nevezhetjük a három szám logaritmikus közepének.