Kezdőlap


Cím:	Latin négyzetek II.
Szerző(k):	Dénes Tamás
Füzet:	2005/május, 262 - 269. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A cikk első részében megismert latin négyzetek gyakorlati alkalmazásai főleg három területre irányulnak:

$a)$	statisztikus kísérlet-tervezés

$b)$	kódolás (hírközlés)

$c)$	titkosítás.

Míg a statisztikai alkalmazásokban R. A. Fisher tekinthető úttörőnek, az 1920-as években megkezdett tevékenységével és híres könyvével (The design of experiments), addig a latin négyzetek hírközlésben való alkalmazása a II. világháborút megelőzően, illetve alatta kezdődött amerikai és német részről egyaránt. Az első eredmények azonban, érthető okokból, csak a háború befejezése után jelentek meg. Amerikai részről C. E. Shannon, német részről Rudolf Schauffler (a német rejtjelfejtés kimagasló alakja a II. világháború alatt) nevét kell megemlíteni úttörőként.

Alkalmazások a statisztikus kísérlet-tervezésben

Képzeljük el, hogy egy folyamat eredményét (ami lehet pl. egy adott termék minősége, egy kombinált gyógyszerterápia hatásossága, egy haszonnövény termőképessége stb.) több tényező is befolyásolhatja. Az eredményt esetlegesen befolyásoló tényezők különböző állapotai együttesen alakítják ki a végeredményt; meg szeretnénk tudni, melyek azok a paraméterek, amelyek ebből a szempontból a legfontosabbak, és milyen állapotuk biztosítja a legkedvezőbb eredményt. Ennek a kiderítésére természetesen az lenne a legkézenfekvőbb, ha a folyamatot valamennyi paraméter minden egyes állapotában ,,lejátsszuk'', és az egyes kimeneteleket értékelve megkeressük a paraméteregyüttesnek azt a ,,beállítását'', amelyik a legjobb végeredményre vezet. Ez a ,,biztos'' megoldás azonban a legtöbb esetben igen nagy számú, következésképpen hosszú ideig tartó és roppant költséges kísérletezést jelent.
Elsőként R. A. Fisher mutatott rá, hogy az addigi gyakorlattal szemben ‐ amikor a kísérletek során egyetlen tényezőt változtattak ‐ célszerű az összes tényező (az úgynevezett faktorok) egyidejű variálása. Így jött létre a statisztika egy új ága, a faktor-analízis, valamint ekkor jelentek meg a latin négyzetek a kísérletek tervezésében.
Az ortogonális latin négyzetek statisztikai alkalmazását egy példán mutatom be. Ötféle kikészítésű szálból szőtt késztermék mintázatát kell minőségileg összehasonlítani. A késztermék előállításán öt szövőgépen öt gépkezelő dolgozik. Az a feltételezés (amit igazolni kell), hogy a szálak kikészítésén kívül a szövéshez felhasznált gép és annak kezelője is a minőséget befolyásoló tényezők. Ha a kísérletekre szánt idő nem lenne korlátozó tényező, akkor minden egyes fonalfajtát mind az öt szövőgépen az öt gépkezelő mindegyikével ki kellene próbálni. Ez összesen 125 kísérletet jelent. A latin négyzetek segítségével azonban kielégítő eredményt lehet elérni egy 25 kísérletből álló kísérletsorozattal is. Jelölje

K_{1}, K_{2}, ..., K_{5}

az öt gépkezelőt,

S_{1}, S_{2}, ..., S_{5}

az öt szövőgépet,

Y_{1}, Y_{2}, ..., Y_{5}

pedig az öt különféle szálat.
A minőség összevetésére szolgáló 25 kísérletet az 1/a. ábrán bemutatott latin négyzet ábrázolja.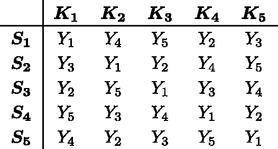

1/a. ábra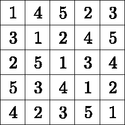

1/b. ábra

Az 1/a. ábrán látható latin négyzet úgy alkalmazható a kísérlet megtervezésében, hogy az oszlop-kiválasztással a kezelőt, a sor-kiválasztással a szövőgépet és a kiválasztott sor és oszlop metszetében álló elemmel pedig az adott kísérletben felhasznált fonalat határozzuk meg. Így például az első kísérletben a

K_{1}

gépkezelő az

S_{1}

szövőgépen

Y_{1}

fonallal dolgozik.
Tegyük fel továbbá, hogy a gépkezelők munkáját befolyásolja, hogy a hét melyik munkanapján dolgoznak. Ekkor az 1/a. ábrán megadott latin négyzetben szereplő indexekhez (lásd 1/b. ábra) ortogonális párt kell szerkeszteni (lásd 2/a. ábra), ahol a munkanapokat számok jelzik. (1 = hétfő, 2 = kedd, 3 = szerda, 4 = csütörtök, 5 = péntek.)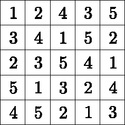

2/a. ábra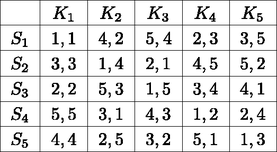

2/b. ábra

A két ortogonális latin négyzetet (lásd az 1/b. és 2/a. ábrán) egymásra helyezve adódó 25 kísérletből álló kísérletsorozatot ábrázolja a 2/b. ábra. Így minden egyes gépkezelő minden egyes szövőgépen dolgozik, a munkájában az öt különböző kikészítésű fonal mindegyikét pontosan egyszer használja, és a vele kapcsolatos kísérleteknél egy hét 5 munkanapja közül minden napra egy kísérlet jut. Hasonló típusú kísérleteket végeznek például a növénytermesztés, vagy a gyógyszerkutatás során is.
Nyilvánvaló, hogy a kísérlet tervezésénél a latin négyzetek felhasználása bizonyos szempontból korlátozott, hiszen ha az előbbi példánkban például a gépkezelők száma nem öt, hanem négy, akkor már másfajta elrendezésre van szükség. Az ilyen, a latin négyzeteknél általánosabb elrendezéseket blokkrendszereknek nevezzük. Az érdeklődő olvasó jó betekintést kaphat ezekről [6]-ból.
Egy másik példa világítja meg a teljes latin négyzetek alkalmazását a kísérletek tervezésében. Egy állatkísérletben a kísérleti állatokat különböző étrend szerint táplálják, a feltevés szerint (amelyet a kísérletek során ellenőrizni kívánnak) egy adott állat etetése előtt, a kísérlet során lezajlott étkezések száma, valamint a közvetlenül megelőző etetés során kapott takarmány fajtája befolyásolja az eredményt.
Tegyük fel, hogy

n

darab állatot és

n

-féle takarmányt vizsgálunk.

n = 4

esetén az

A_{1}, A_{2}, A_{3}, A_{4}

kísérleti állatokat a

T_{1}, T_{2}, T_{3}, T_{4}

takarmányokkal táplálják a 3. ábrán látható teljes latin négyzet szerinti elrendezésben.
Ez az elrendezés (3. ábra) azt jelenti, hogy például az

A_{1}

állatnak első étkezésre a

T_{1}

takarmányt, másodikra a

T_{2}

takarmányt stb. kell adni. A kísérletsorozatban valóban fontos a teljes latin négyzet tulajdonság (ennek definíciója e cikk I. részében¹ található), hiszen ez biztosítja, hogy az összes lehetséges takarmány-sorrendet kipróbáljuk.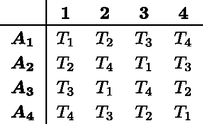

3. ábra

Kódoláselméleti alkalmazások

Az elsősorban a távközlésben használt hibajavító (blokk) kódolás során az elküldeni kívánt üzeneteket

k

hosszúságú sorozatokká (blokkokká) alakítjuk. A sorozat elemei egy

q

-elemű halmaz (ábécé) tetszőleges elemei lehetnek. (A leggyakoribb esetben

q = 2

, ekkor bináris kódról beszélünk.) Ha ezeket a blokkokat küldjük el, akkor védtelenek vagyunk minden ,,útközben'' keletkezett hibával szemben: ha a blokk egy vagy több eleme valamilyen zavaró hatás miatt megváltozik, az üzenet címzettje kénytelen azt elfogadni, hiszen az ábécéből képezhető valamennyi

k

hosszúságú sorozat lehet küldésre szánt blokk.
A problémát a következőképpen próbálják megoldani: az eredeti

k

-as blokkot valamilyen kódolási eljárás segítségével egy

n

hosszúságú sorozattá (kódszóvá) alakítják, ahol

n > k

. Így persze nem kaphatunk meg minden

n

hosszúságú sorozatot kódszóként, ami a következő esélyt kínálja: ha az elküldött kódszó úgy változik meg, hogy az ennek nyomán keletkező blokk nem szerepel a kódszavak között, akkor a rendszer jelzi a hibát, vagyis a címzett biztos lehet benne, hogy a kapott üzenet hibás. Ennél azonban több is elérhető: ha a kódolás eredményeképpen bármely két kódszó ,,sok'' helyen különbözik egymástól, akkor egy kódszó viszonylag kismértékű megváltozása esetén még rekonstruálhatjuk az eredeti üzenetet, illetve az annak megfelelő kódszót. Mindössze azt a kódszót kell megkeresnünk, amelyik a kapott sorozattól a legkevesebb helyen tér el. Ezt valósítják meg a hibajavító kódok.
Az elmondottak pontosabb megfogalmazásához be kell vezetnünk a távolság fogalmát. Két

n

hosszúságú kódszó

a = (a_{1} a_{2} ... a_{n})

és

b = (b_{1} b_{2} ... b_{n})

közötti Hamming-távolság (jele:

d (a, b)

), azon

i

(

i = 1,2, ..., n

) indexek száma, amelyekre

a_{i} \neq b_{i}

.
Egy kódnak a minimális Hamming-távolsága a kódban szereplő összes kódszó párok közötti Hamming-távolságok minimuma.
Jelölje egy kód minimális Hamming-távolságát

d

. Ekkor minden olyan meghibásodásról tudomásunk lesz, melynek során egy kódszó legfeljebb

d - 1

helyen változott meg; azt mondjuk, hogy a kódunk

d - 1

hibát jelez. Sőt, az is könnyen belátható, hogy ha egy kódszó legfeljebb

\frac{d - 1}{2}

helyen változik meg, akkor az eredeti szó egyértelműen visszaállítható: a kód

\frac{d - 1}{2}

-hibajavító.
A latin négyzeteken alapuló nem bináris hibajelző és javító kódok elterjedéséhez a feltételt a szélessávú űrtávközlési csatornák megjelenése teremtette meg. S. W. Golomb és E. C. Posner, a JPL (Jet Propulation Laboratory) pasadenai kutató laboratórium vezető munkatársai foglalkoztak a hibajelző és -javító kódok latin négyzetek alapján való szerkesztésével. Eredményük szerint:
Ha létezik

t

darab

n

-ed rendű latin négyzetből álló ortogonális rendszer, akkor létezik olyan

t + 2

hosszúságú kódszavakból álló kód, amelynek minimális Hamming-távolsága

t + 1

, és amelyben

n^{2}

kódszó van.
Alapvető tétel, hogy egy

q

betűből álló ábécé feletti

k

hosszúságú

d

minimális Hamming-távolságú kódban legfeljebb

q^{k - d + 1}

kódszó lehet. Így a Golomb‐Posner kódban a kódszavak száma

n^{t + 2 - (t + 1) + 1} = n^{2}

, ami

n

-ed rendű latin négyzetek esetén maximális.
A Golomb‐Posner kód konstrukciója a következő példán jól követhető: Legyen

n = 4

, a konstrukcióhoz az

L_{1}, L_{2}, L_{3}

páronként ortogonális negyedrendű latin négyzeteket használjuk fel (lásd 4. ábra).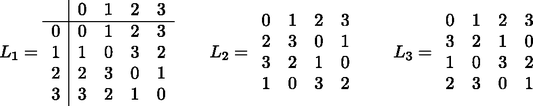

4. ábra

L_{1}

-hez a keret-elemeket is feltüntettük, mivel ennek a kódszavak képzése során jelentősége lesz. A kódszavakat a következő módon képezzük: az első komponens a sorkeret egyik eleme,

a_{i}

(

i = 1,2,3,4

), a második komponens az oszlopkeret egyik

b_{j}

(

j = 1,2,3,4

) eleme, majd sorrendben ezen keret-elemek után következnek az

L_{1}, L_{2}, L_{3}

latin négyzetek belsejében az

a_{i}

sor és a

b_{j}

oszlop metszésénél lévő elemek. Így a 4. ábra

L_{1}, L_{2}, L_{3}

latin négyzeteiből az 5. ábrán lévő kódszó-készlethez jutunk. Az olvasó ellenőrizheti, hogy a kódszavak száma

4^{2} = 16

, a szóhossz 5, a minimális Hamming-távolság 4.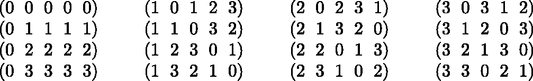

5. ábra

Az I. részben említett tizedrendű latin négyzetekből álló ortogonális rendszer létrehozásának problémája (létezik-e három 10-ed rendű latin négyzetből álló ortogonális rendszer?) most a kódok nyelvére lefordítva így hangzik: van-e olyan Golomb‐Posner kód, amelyben a 10 elemű ábécé feletti kódszavak száma 100, hosszuk 5 és a kód minimális Hamming-távolsága 4?
A Golomb‐Posner kódok előnye, hogy

n \neq 2

, illetve

n \neq 6

esetén tetszőleges

n

elemű ábécé felett léteznek. [2]-ben sikerült a Golomb‐Posner féle konstrukciót ortogonális latin téglalapokra általánosítani.
A latin téglalap olyan téglalap mátrix, amely kiegészíthető latin négyzetté. Két azonos méretű latin téglalapot akkor nevezünk ortogonálisnak, ha egymásra helyezve őket a megfelelő rendezett párok mind különbözőek.
Példát mutatunk be a párok [2]-ben közölt konstrukciója alapján arra, hogy a

2 \times 6

-os

R_{1}, R_{2}, R_{3}, R_{4}, R_{5}

latin téglalapokból álló ortogonális rendszerből (lásd 6. ábra) milyen kód nyerhető.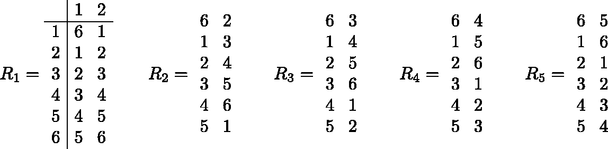

6. ábra

A konstrukció követhetősége érdekében

R_{1}

-nél a perem elemeket is feltüntettük. A konstrukció a latin négyzetekre alkalmazott Golomb‐Posner eljárásnak értelemszerű megfelelője. Az így kapott kód elemeit (kódszavait) a 7. ábrán láthatjuk.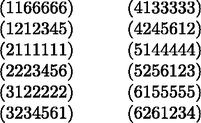

7. ábra

A fenti konstrukció felhasználható személyi számok, jogosítvány, vagy ISBN számok, valamint más hasonló kódok előállítására. A rendszer ortogonálisa miatt a keletkező kódszavak különbözőek, az eljárás könnyen programozható, gyors előállítást kínál.

Alkalmazás a digitális kép-kódolás és átvitel területén

Egy

(0; 1)

mátrixról akkor mondjuk, hogy

u \times v

(

u, v \geq 2

) horizontális ablak tulajdonsággal rendelkezik, ha egy

u

sorból és

v

oszlopból álló ablakot vízszintesen mozgatva a mátrixon, minden nem csupa nullából álló ablak legfeljebb egyszer fordul elő. (Hasonlóképpen definiáljuk a vertikális ablak tulajdonságot.)
Egy mátrixot akkor mondunk

u \times v

ablak tulajdonságúnak, ha horizontálisan is és vertikálisan is

u \times v

ablak tulajdonságú.
Természetes alkalmazás, ha egy latin négyzetről követeljük meg a horizontális, illetve vertikális ablak tulajdonságot.

(0; 1)

mátrixokra az ablak tulajdonságot két, a Bell laboratóriumban dolgozó matematikus (F. J. MacWilliams és N. J. A. Sloane) vizsgálta először. Az ablak tulajdonsággal rendelkező mátrixok a gyakorlatban is alkalmazhatók, például képek digitális kódolása és adatátvitel területén.
A következő példa ablak tulajdonságokkal rendelkező mátrix szerkesztését mutatja be, teljes latin négyzetek felhasználásával.
Tekintsünk egy negyedrendű teljes

L_{4} (a_{i j})

latin négyzetet (lásd 8. ábra), majd utolsó oszlopát megismételve, valamint egy kizárólag ötösöket tartalmazó oszlopot hozzávéve készítsük el a 9. ábrán látható

M_{4 \times 6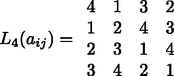} (b_{i j})

mátrixot.

8. ábra

9. ábra

A teljes latin négyzet tulajdonságból következik, hogy a 8. ábra

L_{4} (a_{i j})

latin négyzete is és a 9. ábra

M_{4 \times 6} (b_{i j})

kiterjesztése is rendelkezik a vertikális, illetve horizontális

2 \times 2

ablak tulajdonsággal.
Vesszőmentesnek nevezünk egy olyan

C

kódot, amely

n

hosszúságú szavakból áll, és bármely

a_{1} ... a_{n} \in C

és

b_{1} ... b_{n} \in C

esetén az

a_{j} a_{j + 1} ... a_{n} b_{1} b_{2} ... b_{j - 1}

(

j = 2,3, ..., n

) sorozatok egyike sincsen

C

-ben.
Szemléltető példaként a 9. ábra mátrixát és a 10. ábra bináris vesszőmentes kódját felhasználva, az

i, j \leftrightarrow c_{b_{i j}}

(

i = 1,2,3,4

j = 1,2,3,4,5,6

) megfeleltetéssel nyerjük a 11. ábrán látható

(0; 1)

mátrixot, amely

14 \times 1

ablak tulajdonságú.

10. ábra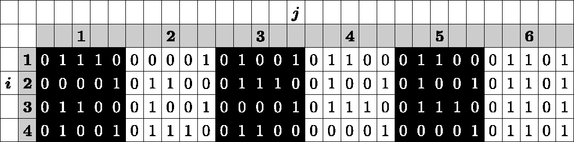

11. ábra

A fenti latin négyzeteket felhasználó szerkesztési mód részletes leírása megtalálható [3]-ban.
A latin négyzetek jelen dolgozat elején jelzett c)-típusú, azaz a titkosításban való alkalmazásáról már e folyóirat hasábjain a [4] cikkben olvasható egy fontos példa. További érdekes alkalmazásokat talál az érdeklődő olvasó a www.titoktan.hu honlap e-világi gondolatok oldalán.

Hivatkozások

[1]	A. M. Andrew: Decimal error-correction: a solution.

[2]	J. Dénes: Latin squares and non-binary encoding, Proc. Conf. Information Theory (Cachen, France, 1977), CNRS, Paris (1979), 215‐221.

[3]	J. Dénes, A. D. Keedwell: A new construction of twodimensional arrays with window property, IEEE Trans. On Information Theory (1988).

[4]	Dénes Tamás: Cardano és a kriptográfia. A rejtjelző-rácsok matematikája, Középiskolai Matematikai és Fizikai Lapok, 51. évfolyam, 2001/6.

[5]	A. Ecker and G. Poch: Check character systems, Computing, 37 (1986), 289‐297.

[6]	Lovász ‐ Pelikán ‐ Vesztergombi: Kombinatorika, Typotex Kiadó (Budapest).

[7]	D. H. Lehmer: A photo-electric number sieve, Amer. Math. Monthly, 40 (1933), 401‐406.

[8]	D. H. Lehmer: A machine for combining sets of linear conqruences, Mathematische Annalen, 109 (1934), 661‐667.

[9]	R. Mandl: Orthogonal latin squares: an application of experimental design to compiler testing, Comm. ACM, 28 (1985), 1054‐1058.

¹Ld. KöMaL 2005/4. sz., 194. oldal.