Kezdőlap


Cím:	A számok hatványainak összegéről 3.
Szerző(k):	Buzi K. , Fried E. , Gacsályi S. , Gősy Sándor , Horváth G. , Kalmár László , Kővári Tamás
Füzet:	1948/szeptember, 169 - 176. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

( A VI. Fejezet végén felvetett kérdésekre érkezett válaszok megbeszélése.)

VII.

a) Az első

n

szám köbének összegezésére induljunk ki a

{(k + 1)}^{3} = k^{3} + 3 k^{2} + 3 k + 1

képletből

(k + 1)

-gyel való ,,beszorzással'' kapható

\begin{matrix} {(k + 1)}^{4} = k^{4} + 4 k^{3} + 6 k^{2} + 4 k + 1 \end{matrix}

azonosságból. Ezt

k^{3}

-re megoldva

\begin{matrix} k^{3} = \frac{{(k + 1)}^{4}}{4} - \frac{k^{4}}{4} - \frac{3}{2} k^{2} - k - \frac{1}{4} . \end{matrix}

k

helyébe 0-t, 1-et, 2-t, 3-at,

...

n

-et téve:

\begin{matrix} 0^{3} & = \frac{1^{4}}{4} - \frac{1}{4}, \\ 1^{3} & = \frac{2^{4}}{4} - \frac{1^{4}}{4} - \frac{3}{2} \cdot 1^{2} - 1 - \frac{1}{4}, \\ 2^{3} & = \frac{3^{4}}{4} - \frac{2^{4}}{4} - \frac{3}{2} \cdot 2^{2} - 2 - \frac{1}{4}, \\ \dots \dots \dots \dots \dots \dots \\ n^{3} & = \frac{{(n + 1)}^{4}}{4} - \frac{n^{4}}{4} - \frac{3}{2} \cdot n^{2} - n - \frac{1}{4} . \end{matrix}

Összeadva

\begin{matrix} 1^{3} + 2^{3} + 3^{3} + ... + n^{3} = \frac{{(n + 1)}^{4}}{4} - \frac{3}{2} \cdot (1^{2} + 2^{2} + 3^{2} + ... + n^{2}) - (1 + 2 + 3 + ... + n) - \frac{n + 1}{4} = \end{matrix}

\begin{matrix} = \frac{{(n + 1)}^{4}}{4} - \frac{3}{2} \frac{n (n + 1) (2 n + 1)}{6} - \frac{n (n + 1)}{2} - \frac{n + 1}{4} = \\ = \frac{{(n + 1)}^{4} - n (n + 1) (2 n + 1) - 2 n (n + 1) - (n + 1)}{4} = \\ = \frac{{(n + 1)}^{4} - n (n + 1) (2 n + 1) - (n + 1) (2 n + 1)}{4} = \\ = \frac{{(n + 1)}^{4} - (n + 1) (2 n + 1) (n + 1)}{4} = \\ = \frac{{(n + 1)}^{2} ({(n + 1)}^{2} - (2 n + 1))}{4} = \\ = \frac{{(n + 1)}^{2} n^{2}}{4} = {(\frac{n (n + 1)}{2})}^{2} . \end{matrix}

Gősy Sándor (Orosházi ev. gimn. VIII. o.)

Megjegyzés: Az eredmény a következő alakban is írható:

\begin{matrix} 1^{3} + 2^{3} + 3^{3} + ... + n^{3} = {(1 + 2 + 3 + ... + n)}^{2} \end{matrix}

Ezt az érdekes összefüggést Fried E. és Horváth G. is észreveszi, Buzi K. pedig tapasztalati úton jön rá.
5. feladat: hogyan lehetne ezt közvetlenül, geometriailag vagy másképpen bebizonyítani?
b) Az első

n

szám negyedik hatványának összegezésre ,,szorozzuk be'' a

{(k + 1)}^{4} = k^{4} + 4 k^{3} + 6 k^{2} + 4 k + 1

képletet

(k + 1)

-gyel és oldjuk meg a kapott

\begin{matrix} {(k + 1)}^{5} = k^{5} + 5 k^{4} + 10 k^{3} + 10 k^{2} + 5 k + 1 \end{matrix}

azonosságot

k^{4}

-re nézve. Az így keletkező

\begin{matrix} k^{4} = \frac{{(k + 1)}^{5}}{5} - \frac{k^{5}}{5} - 2 k^{3} - 2 k^{2} - k - \frac{1}{5} \end{matrix}

azonosságban

k

helyébe 0-t, 1-et, 2-t, 3-at,

...

n

-et téve és összegezve, azt kapjuk, hogy

\begin{matrix} 1^{4} + 2^{4} + 3^{4} + ... + n^{4} = \frac{{(n + 1)}^{5}}{5} - 2 (1^{3} + 2^{3} + 3^{3} + ... + n^{3}) - \end{matrix}

\begin{matrix} - 2 (1^{2} + 2^{2} + 3^{2} + ... + n^{2}) - (1 + 2 + 3 + ... + n) - \frac{n + 1}{5} = \end{matrix}

\begin{matrix} = \frac{{(n + 1)}^{5}}{5} - 2 \frac{{(n + 1)}^{2} n^{2}}{4} - 2 \frac{n (n + 1) (2 n + 1)}{6} - \frac{n (n + 1)}{2} - \frac{n + 1}{5}, \end{matrix}

amiből a szokott algebrai átalakításokkal (közös nevezőre hozás, beszorzás, összevonás)

\begin{matrix} 1^{4} + 2^{4} + 3^{4} + ... + n^{4} = \frac{6 n^{5} + 15 n^{4} + 10 n^{3} - n}{30} . \end{matrix}

Gősy Sándor (Orosházi ev. gimn. VIII. o.)

Megjegyzés: Akármennyire belénk rögződtek is azok a bizonyos ,,szokott algebrai átalakítások'', semmi szükség nincs rá, hogy álmunkból felkeltve is mindig azokat végezzük, gondolkodás nélkül. Ha pl. az első 37 szám negyedik hatványának összegét akarjuk kiszámítani, elég keserves számítás volna 37-et ötödik, negyedik, harmadik hatványra emelni, e hatványokat rendre 6-tal, 15-tel és 10-zel megszorozni, a szorzatokat összeadni, összegükből 37-et kivonni s a különbséget 30-cal elosztani. Aki kevésbé ,,szokásos'', de ügyesebb algebrai átalakításokkal

(n + 1)

kiemelése, majd az első tagban az

{(n + 1)}^{4} = n^{4} + 4 n^{3} + 6 n^{2} + 4 n + 1

azonosság alkalmazása és utolsó taggal való összevonás után

n

kiemelése, a zárójelen a ,,szokott algebrai átalakítások'' után a számláló tényezőkre bontása stb.) az

\begin{matrix} 1^{4} + 2^{4} + 3^{4} + ... + n^{4} = \frac{n (n + 1) (2 n + 1) (3 n (n + 1) - 1)}{30} \end{matrix}

eredményt kapja, sokkal célszerűbb eljáráshoz jut az első

n

szám negyedik hatványa összegének kiszámítása Pl. Ha

n = 37

n + 1 = 38

n (n + 1) = 37 \cdot 38 = 1406

2 n + 1 = 75

3 n (n + 1) - 1 = 3 \cdot 1406 - 1 = 4217

, tehát

\begin{matrix} 1^{4} + 2^{4} + 3^{4} + ... + 37^{4} = \frac{1406 \cdot 75 \cdot 4217}{30} = 703 \cdot 5 \cdot 4217 = 14.822.755. \end{matrix}

c) Az első

n

szám ötödik hatványának hasonló módszerrel való összegezésére már nem futotta egyik olvasónk türelme sem. Azonban többen megfogalmazták ezt a módszert általánosan. Szükségünk van hozzá a

{(k + 1)}^{2} = k^{2} + 2 k + 1

{(k + 1)}^{3} = k^{3} + 3 k^{2} + 3 k + 1

{(k + 1)}^{4} = k^{4} + 4 k^{3} + 6 k^{2} + 4 k + 1

{(k + 1)}^{5} = k^{5} + 5 k^{4} + 10 k^{3} + 10 k^{2} + 5 k + 1

képletek általánosítására tetszőleges kitevőre. Könnyű látni (teljes indukcióval), hogy minden kitevőre van ilyenféle azonosság, azaz

{(k + 1)}^{m}

m

minden pozitív egész értéke mellett

k

hatványai szerint rendezhető (és, csökkenő hatványok szerint rendezve,

k^{m} + m k^{m - 1}

-gyel kezdődik). Ha ugyanis ez valamilyen

m

-re áll,

(k + 1)

-gyel "beszorozva'' és összevonva, látjuk, hogy

m

helyett

(m + 1)

-gyel is áll (s a legmagasabb fokú tag

k^{m} \cdot k = k^{m + 1}

lesz, a következő tag pedig az

m k^{m - 1} \cdot k = m k^{m}

és

k^{m} \cdot 1 = k^{m}

összevonásából keletkező

(m + 1) k^{m})

. A

{(k + 1)}^{m}

ilyen, csökkenő hatványai szerint menő előállításában (u. n. binomiális kifejtésében) az együtthatókat (az u. n. binomiális együtthatókat) sorra az

(\binom{m}{0})

(\binom{m}{1})

(\binom{m}{2}), ..., (\binom{m}{m})

, jelekkel (ejtsd:

m

alatt 0,

m

alatt 1,

m

alatt

2, ..., m

alatt

m

) jelöljük. (Más kapcsolatában találkoztunk velük Csebysev tétele kapcsán. L. 155. feladat. 123. a.). Pl.

(\binom{1}{0}) = (\binom{1}{1}) = 1

(\binom{2}{0}) = 1

(\binom{2}{1}) = 2

(\binom{2}{2}) = 1

(\binom{5}{0}) = 1

(\binom{5}{1}) = 5

(\binom{5}{2}) = (\binom{5}{3}) = 10

(\binom{5}{4}) = 5

(\binom{5}{5}) = 1

(és általánosan

(\binom{m}{0}) = 1

(\binom{m}{1}) = m

és

(\binom{m}{m}) = 1

; az utóbbi miért ?) Vagyis

{(k + 1)}^{m}

-binomiális kifejtése így szól:

\begin{matrix} {(k + 1)}^{m} = k^{m} + (\binom{m}{1}) k^{m - 1} (\binom{m}{2}) k^{m - 2} + ... + (\binom{m}{m - 1}) k + 1. \end{matrix}

Az első

n

szám

m

-edik hatványának összegezéséhez

{(k + 1)}^{m + 1}

binomiális kifejtésére:

\begin{matrix} {(k + 1)}^{m + 1} = k^{m + 1} + (\binom{m + 1}{1}) k^{m} + (\binom{m + 1}{2}) k^{m - 1} + ... + (\binom{m + 1}{m}) k + 1 \end{matrix}

van szükség, amit

k^{m}

-re megoldva így is írhatunk:

\begin{matrix} k^{m} = \frac{{(k + 1)}^{m + 1}}{m + 1} - \frac{k^{m + 1}}{m + 1} - \frac{1}{m + 1} (\binom{m + 1}{2}) k^{m - 1} - ... - \\ - \frac{1}{m + 1} (\binom{m + 1}{m - 1}) k^{2} - \frac{1}{m + 1} (\binom{m + 1}{m}) - \frac{1}{m + 1} . \end{matrix}

Ha ebben helyettesítünk

k

helyébe sorra 0-t, 1-et, 2-t, 3-at,

..., n

-et és a kapott egyenleteket összeadjuk, kapjuk, hogy

\begin{matrix} 1^{m} + 2^{m} + 3^{m} + ... + n^{m} = \frac{1}{m + 1} [{(n + 1)}^{m + 1} - \\ - (\binom{m + 1}{2}) (1^{m - 1} + 2^{m - 1} + 3^{m - 1} + ... + n^{m - 1}) - \\ - ... - (\binom{m + 1}{m - 1}) (1^{2} + 2^{2} + 3^{2} + ... + n^{2}) - \\ - (\binom{m + 1}{m}) (1 + 2 + 3 + ... + n) - (n + 1)] \end{matrix}

Ez u. n. rekurzív képletet szolgáltat

1^{m} + 2^{m} + 3^{m} + ... + n^{m}

számára; ha

1 + 2 + 3 + ... + n

1^{2} + 2^{2} + 3^{2} + ... n^{2}

1^{3} + 2^{3} + 3^{3} + ... + n^{3}

1^{m - 1} + 2^{m - 1} + 3^{m - 1} + ... + n^{m - 1}

, számára már van a fentiekhez hasonló képletünk, innét kaphatunk

1^{m} + 2^{m} + 3^{m} + ... + n^{m}

számára is.

Kővári Tamás (Bp. ev. gimn. VIII. o.)

Gacsályi S. a fenti rekurzív képletből

m

helyébe 5-öt téve és a

(\binom{6}{2}) = 15

(\binom{6}{3}) = 20

(\binom{6}{4}) = 15

(\binom{6}{5}) = 6

értékeket behelyettesítve (ezekhez persze úgy jutunk, hogy

{(k + 1)}^{5}

binomiális kifejtését "beszorozzuk''

(k + 1)

-gyel), a következő összegképlethez jut:

\begin{matrix} 1^{5} + 2^{5} + 3^{5} + ... + n^{5} = \frac{1}{6} [{(n + 1)}^{6} - 15 (1^{4} + 2^{4} + 3^{4} + ... + n^{4}) - \\ - 20 \cdot (1^{3} + 2^{3} + 3^{3} + ... + n^{3}) - 15 \cdot (1^{2} + 2^{2} + 3^{2} + ... + n^{2}) \\ - 6 (1 + 2 + 3 + ... + n) - (n + 1)] = \\ = \frac{1}{6} [{(n + 1)}^{6} - \frac{n (n + 1) (2 n + 1) (3 n (n + 1) - 1)}{2} - 5 n^{2} {(n + 1)}^{2} - 5 \frac{n (n + 1) (2 n + 1)}{2} - 3 n (n + 1) - (n + 1)], \end{matrix}

ahonnan a ,,szokott algebrai átalakításokkal'' az

\begin{matrix} 1^{5} + 2^{5} + 3^{5} + ... + n^{5} = \frac{2 n^{6} + 6 n^{5} + 5 n^{4} - n^{2}}{12} \end{matrix}

képletet kapja (még 1 pont). Ki tudná ezt ügyesebb alakra hozni?

Megjegyzés:

m = 1

, 2, 3, 4, 5 esetében azt tapasztaltuk (és a fenti rekurzív képletből teljes indukcióval általánosan is igazolhatjuk), hogy

1^{m} + 2^{m} + 3^{m} + ... + n^{m}

n

-nek

(m + 1)

-edfokú polinomjaként írható. Tegyük fel, hogy valamely

m

-re már sikerült

1^{m} + 2^{m} + 3^{m} + ... + n^{m}

-et ilyen módon előállítanunk:

\begin{matrix} 1^{m} + 2^{m} + 3^{m} + ... + n^{m} = a_{0} n^{m + 1} + a_{1} n^{m} + a_{2} n^{m - 1} + ... + a_{m} n \end{matrix}

(ahol

a_{0}, a_{1}, ..., a_{m}

nem szükségképpen egész számok;

n

nélküli tag nem szerepelhet, miért ?). Akkor

1^{m + 1} + 2^{m + 1} + 3^{m + 1} + ... + n^{m + 1}

számára a következőképen is sikerül hasonló előállítást kapnunk:

\begin{matrix} 1^{m + 1} + 2^{m + 1} + 3^{3 + 1} + ... + n^{m + 1} = 1^{m} + 2^{m} + 3^{m} + ... + n^{m} + \\ + 2^{m} + 3^{m} + ... + n^{m} + \\ + 3^{m} + ... + n^{m} + \\ + ... + n^{m} + \\ + \cdot \cdot \cdot + \\ + n^{m} = \\ = (n + 1) (1^{m} + 2^{m} + 3^{m} + ... + n^{m}) - (1^{m} + (1^{m} + 2^{m}) + (1^{m} + 2^{m} + 3^{m}) + \\ + ... + (1^{m} + 2^{m} + 3^{m})) = \\ = (n + 1) (1^{m} + 2^{m} + 3^{m} + ... + n^{m}) - (a_{0} \cdot 2^{m + 1} + a_{1} \cdot 2^{m} + a_{2} \cdot 2^{m - 1} + ... + a_{m} \cdot 1 + \\ + a_{0} \cdot 2^{m + 1} + a_{1} \cdot 2^{m} + a_{2} \cdot 2^{m - 1} + ... + a_{m} \cdot 2 + \\ + \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot + \\ + a_{0} \cdot n^{m + 1} + a_{1} \cdot n^{m} + a_{2} \cdot 2^{m - 1} + ... + a_{m} \cdot n) = \\ = - a_{0} (1^{m + 1} + 2^{m + 1} + 3^{m + 1} + ... + n^{m + 1}) + (n - a_{1} + 1) (1^{m} + 2^{m} + 3^{m} + ... + \\ + n^{m}) - a_{2} (1^{m + 1} + 2^{m + 1} + 3^{m + 1} + ... + n^{m + 1}) - ... - a_{m} (1 + 2 + 3 + ... + n) . \end{matrix}

Ezt az egyenletet

1^{m + 1} + 2^{m + 1} + 3^{m + 1} + ... + n^{m + 1}

-re megoldva (meg lehet oldani; miért?) olyan képletet kapunk, amelyből

1^{m + 1} + 2^{m + 1} + 3^{m + 1} + ... + n^{m + 1}

-et is sikerül a fenti alakra hozni, ha

1 + 2 + 3 + ... + n

-et,

1^{2} + 2^{2} + 3^{2} + ... + n^{2}

-et,

1^{m} + 2^{m} + 3^{m} + ... + n^{m}

-et sikerült. Gacsályi ezen a módon is lehozza a fenti képleteket

1^{3} + 2^{3} + 3^{3} + ... + n^{3},

1^{4} + 2^{4} + 3^{4} + ... + n^{4}

1^{5} + 2^{5} + 3^{5} + ... + n^{5}

számára.
6. Feladat: Ha már tudjuk, hogy

1^{m} + 2^{m} + 3^{m} + ... + n^{m}

előállítható

a_{0} n^{m + 1} + a_{1} n^{m} + a_{2} n^{m - 1} + ... + a_{m} n

alakban, csak

a_{0}

a_{1}

a_{2}, ..., a_{m}

számértékét nem ismerjük (vagy már elfelejtettük), vajon hogyan határozhatjuk meg őket könnyen?

VIII.

Az 1‐4. kérdésekre csak ketten küldtek feleletet. Gacsályi feleletei lényegében jók; Horváth Szabolcs azonban félreérti a kérdést, nem a geometriai okoskodásokat fordítja le algebrára, csak a végeredményüket. (Kedves humorát, sajnos, nem tudjuk pontszámmal jutalmazni.) Nem akarok e hasábokon levelezést folytatni Gacsályival, ezért csak a 2. kérdés megoldását közlöm mutatóba, hátha mások is kedvet kapnak tőle az 1., 3. és 4. kérdésekkel, amelyeket ezennel újra kiűzök feladatnak, foglalkozni.
A 2. kérdés így szólt: Persze abból is kijön a számok négyzetösszege, hogy húrom piramist össze lehet rakni olyan hasábbá, amelynek az oldalán van még a jobboldali felső 17. ábrán (2. szám) látható cifraság. Hogyan? Hát ez a geometriai okoskodás hogyan szól algebrául ?
Az első kérdésre könnyű a válasz. A három piramis köbtartalmának összege egyenlő egy olyan hasábével, amelynek élei

n

n + 1

és

n

,,kockányiak'', meg még a cifraság köbtartalmával, vagyis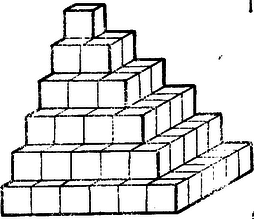

\begin{matrix} 3 (1^{2} + 2^{2} + 3^{2} + ... + n^{2}) = n^{2} (n + 1) + 1 + 2 + 3 + ... + n = \\ = n^{2} (n + 1) + \frac{n (n + 1)}{2} = n (n + 1) (n + 1 / 2) = \frac{n (n + 1) (2 n + 1)}{2}, \end{matrix}

ahonnan

\begin{matrix} 1^{2} + 2^{2} + 3^{2} + ... + n^{2} = \frac{n (n + 1) (2 n + 1)}{6} . \end{matrix}

(Idáig Horváth Szabolcs is eljutott; kap érte két pontot.) Ez azonban még mindig geometriai okoskodás, csak a végét szüreteltük le algebrául. Hogy elejétől végéig algebrai okoskodás legyen belőle, fordítsuk le algebrára a piramisok fordítását is, meg azt is, hogy hárman megfelelően forgatva, a cifrasággal díszített hasábot adják.

Az eredeti helyzetű piramis (l. alsó 17. ábrát!) felülről számított

k

-adik emeletén

k^{2}

kocka van. Hány kis kocka van az oldalra fordított piramisok (l. felső 17. ábrákat!) ugyanazon emeletén?

A bal felső 17. ábráról kis fantáziával könnyű látni, hogy a baloldali piramisnak (amelynek alapja a hasáb bal oldallapjára esik) első (t i. legfelső emeletén

1 + 2 + 3 + ... + n

, a második emeletén (jobbról balra számlálva)

2 + 3 + 4 + ... + n

, a harmadikon

3 + 4 + 5 + ... + n

, általában a

k

-adik emeletén

k + (k + 1) + (k + 2) + ... + n

kis kocka van (az

n

-ediken

n

kis kocka).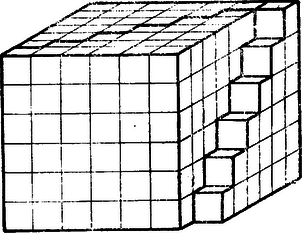

A jobb felső 17. ábra pedig mutatja, hogy ugyanannyi kis kocka van a másik piramisnak egyes emeletein is (amelynek alapja a hasáb elülső lapja). Az tehát, hogy az oldalra fordított piramisok is ugyanannyi kockából állnak, mint az eredeti, algebrául így szól:

\begin{matrix} 1^{2} + 2^{2} + 3^{2} + ... + n^{2} = 1 + 2 + 3 + ... + n + \\ + 2 + 3 + ... + n + \\ + 3 + ... + n + \\ + \cdot \cdot \cdot + \\ + n . \end{matrix}

A fordítással meg lehetünk elégedve, mert e képlet helyessége algebrául is éppoly nyilvánvaló, mint a megfelelő geometriai tényé volt. (És ugyanúgy látjuk is be: az egy-egy oszlopba irt számok összege sorra:

1 = 1

2 + 2 = 2 \cdot 2 = 2^{2}

3 + 3 + 3 = 3 \cdot 3 = 3^{2}

, stb., ami megfelel annak, hogy az oldalra fordított piramisban is sorra

1^{2}

2^{2}

3^{2}

stb. kis kocka van az alapjával párhuzamos rétegekben. ‐ Gacsályi (bevallottan) ennek az azonosságnak általánosításaként jött rá a c) alatti megjegyzésében használt azonosságára. ‐
Azt pedig, hogy a három különböző helyzetű piramis együtt a cifrázott hasábot adja, algebrául így mondhatjuk (egy-egy sorba írva az egy-egy emeleten levő kockák számát):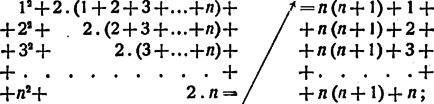

ez meg algebrául úgy látható be, hogy általában bebizonyítjuk, hogy baloldalt a

k

-adik sorban

n (n + 1) + k

áll:

\begin{matrix} k^{2} + 2 \cdot (k + (k + 1) + (k + 2) + ... + n) = k^{2} + 2 \frac{n + k}{2} (n - k + 1) = \\ = k^{2} + (n + k) (n - k + 1) = k^{2} + (n + k) (n - k) + n + k = \\ = k^{2} + n^{2} - k^{2} + n + k = n^{2} + n + k = n (n + 1) + k . \end{matrix}

Igaz, hogy ez nem szó szerinti fordítása annak a geometriai meggondolásnak, amely mutatja, hogy a háromféle helyzetű piramis

k

-adik emelete a hasáb

k

-adik emeletéből épp annyival lóg ki, amennyi a cifraság

k

-adik emelete (l. 54. ábrát).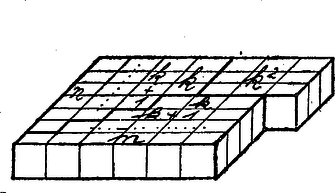

54. ábra

Annak a

k + (k + 1) + (k + 2) + ... + n

számtani sor másfajta, komplikáltabb, összegezése felelne meg, t. i. szintén kétszer írnók fel, de egyik példányát (a 90°-os elforgatásnak megfelelően) "átrendezve''. Azonban nem érdemes a szó szerinti fordításhoz ragaszkodni, különösen, ha már csak egy azonosság belátásáról van szó, hiszen erre az algebrának kezelhetőbb módszerei vannak, mint a geometriának. Az egész okoskodás tehát igy szól algebrául. Mint láttuk,

\begin{matrix} k^{2} + 2 \cdot (k + (k + 1) + (k + 2) + ... + n) = n (n + 1) + k; \end{matrix}

itt

k

helyébe sorra 1-et, 2-t, 3-at,

..., n

-et téve,

\begin{matrix} 1^{2} + 2 \cdot (1 + 2 + 3 + ... + n) = n (n + 1) + 1, \\ 2^{2} + 2 \cdot (2 + 3 + ... + n) = n (n + 1) + 2, \\ 3^{2} + 2 \cdot (3 + ... + n) = n (n + 1) + 3, \\ \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \\ n^{2} + 2 \cdot n = n (n + 1) + n \end{matrix}

összegezve

\begin{matrix} 1^{2} + 2^{2} + 3^{2} + ... + n^{2} + 2 \cdot (1 + 2 & \cdot 2 + 3 \cdot 3 + ... + n \cdot n) = \\ = n \cdot n (n + 1) + 1 + 2 + ... + n, \end{matrix}

azaz

\begin{matrix} 3 \cdot (1^{2} + 2^{2} + 3^{2} + ... + n^{2}) = n^{2} (n + 1) + \frac{n (n + 1)}{2} = \frac{n (n + 1) (2 n + 1)}{2} \end{matrix}

tehát

\begin{matrix} 1^{2} + 2^{2} + 3^{2} + ... + n^{2} = \frac{n (n + 1) (2 n + 1)}{6} . \end{matrix}

Gacsályi ezt mondja el lényegtelen változtatással (nem a vízszintes emeleteken, hanem az oldallapokkal párhuzamos rétegekben levő kockák számát írja fel, jobbról balra); 4 pontot kap érte.
Nos, olvassátok el újra a számok hatványainak összegéről szóld cikk elejét is (5-10. és 39-47. l.) és oldjátok meg minél többen az 1., 3., 4., 5. és 6 feladatot!