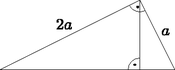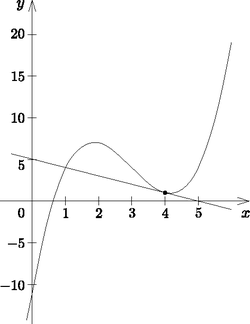Cím:	Megoldásvázlatok a 2005/3. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2005/április, 202 - 207. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Egy derékszögű háromszögben a két befogó hosszának aránya $1:2$, továbbá a kerület és terület mérőszámai egyenlők. Határozzuk meg az átfogóhoz tartozó magasság hosszának pontos értékét.  (11 pont)     Megoldás. A háromszög befogói: $a$, 2$a$, ekkor az átfogója: $a\sqrt[]{5}$. A háromszög területe: $a^2$, a kerülete: $a\left(3+\sqrt[]{5}\right)$. Tudjuk, hogy $a^2=a\left(3+\sqrt[]{5}\right)$. Mivel $a=0$ nem lehet, így $a=3+\sqrt[]{5}$. A háromszög területét az átfogó és az átfogóhoz tartozó magasság segítségével is kiszámíthatjuk: $\begin{array}{c}{\displaystyle T=\frac{a\sqrt[]{5}\cdot m}{2}\mathrm{.}}\end{array}$ A kétféle módon felírt területek egyenlőségéből és az $a$ kiszámolt értékéből kapjuk: $\begin{array}{c}{\displaystyle \frac{\left(3+\sqrt[]{5}\right)\sqrt[]{5}\cdot m}{2}={\left(3+\sqrt[]{5}\right)}^2\mathrm{.}}\end{array}$ Ebből kifejezhető az $m$ értéke: $\begin{array}{c}{\displaystyle m=\frac{2\left(3+\sqrt[]{5}\right)}{\sqrt[]{5}}=\frac{6\sqrt[]{5}+10}{5}\mathrm{.}}\end{array}$   2. Oldjuk meg a következő egyenletrendszert: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle x^2-y^2-6x-6y=0}\\ \hfill {\displaystyle xy-x+y=0}\end{array}}\}}\end{array}$ (12 pont)   Megoldás. Az első egyenletet írhatjuk szorzat alakban: $\left(x+y\right)\left(x-y-6\right)=0$. Ebből következik, hogy $y=-x$ vagy $y=x-6$. Mindkét esetben a második egyenletbe behelyettesítve $x$-re másodfokú egyenletet kapunk. Az első esetben: $x^2+2x=0$. Az ebből kapott $x$ értékekhez kiszámítjuk az $y$-t is: $x_1=0$, $y_1=0$; $x_2=-2$, $y_2=2$. A második esetben: $x^2-6x-6=0$. Az ebből kapott $x$ értékekhez kiszámítjuk az $y$-t is: $x_3=3+\sqrt[]{15}$, $y_3=-3+\sqrt[]{15}$; $x_4=3-\sqrt[]{15}$, $y_4=-3-\sqrt[]{15}$.   3. Egy egyfordulós röplabdakupán ‐ ahol tehát bármely két csapat pontosan egyszer játszik egymással ‐ $30$ lejátszott mérkőzés után még minden csapatnak három mérkőzése volt hátra. Hány csapat szerepelt a kupán?  (14 pont)   Megoldás. Legyen a csapatok száma $n$. Az összes mérkőzések száma: $\frac{n\left(n-1\right)}{2}$. Minden csapatnak még 3 mérkőzése volt hátra, ez összesen $\frac{3n}{2}$ mérkőzés. Ezért a lejátszott mérkőzések száma: $\begin{array}{c}{\displaystyle \frac{n\left(n-1\right)}{2}-\frac{3n}{2}=\mathrm{30,}}\end{array}$ amiből az $n^2-4n-60=0$ másodfokú egyenletet kapjuk. A gyökök: $n_1=10$, $n_2=-6$. A röplabdakupán 10 csapat vett részt.   4. Egy üzem termelése öt egymást követő évben mindig nőtt, az első évben $12$, a másodikban $15$, a harmadikban $20\%$-kal. A negyedik és az ötödik évben a növekedés százaléka azonos volt. Az ötödik évben az üzem a vizsgált időszakot megelőző év termelésének $2\mathrm{,}3$-szeresét érte el. Hány százalékkal növekedett a termelés a negyedik és az ötödik évben?  (14 pont)   Megoldás. Legyen az üzem termelése a vizsgált öt év előtti évben egységnyi, a vizsgált időszak negyedik és ötödik évében a termelés növekedése $p\%$. Legyen $1+\frac{p}{100}=q$. A feladat szövege szerint: $1\mathrm{,}12\cdot 1\mathrm{,}15\cdot 1\mathrm{,}2\cdot q\cdot q=2\mathrm{,}3$, amiből $1\mathrm{,}5456q^2=2\mathrm{,}3$, azaz $q\approx 1\mathrm{,}22$. A termelés a negyedik és az ötödik évben is 22%-kal növekedett.   II. rész   5. $a)$ Az $x^2+bx+c=0$ egyenlet gyökei $2$-vel nagyobbak, mint az $x^2+cx+b=0$ egyenlet gyökei. Számítsuk ki $b$ és $c$ értékét. $b)$ Az $x^2+bx+c=0$ egyenlet egyik gyöke $6$, a másik gyöke egyenlő az egyenlet diszkriminánsával. Számítsuk ki $b$ és $c$ értékét. $c)$ Az $x^2+bx+c$ másodfokú polinom két zérushelye $x_1$ és $x_2$. Írjunk fel olyan harmadfokú polinomot, amelynek zérushelyei: $x_1+x_2$; $x_1^2{x}_2+x_1{x}_2^2$; $x_1^3+x_2^3$.  (16 pont)   Megoldás. $a)$ A második egyenlet gyökei $x_1$ és $x_2$, tehát $x_1+x_2=-c$, $x_1{x}_2=b$. Ekkor $\begin{array}{c}{\displaystyle x_1+2+x_2+2=-c+4=-b\mathrm{,}}\end{array}$ valamint $\begin{array}{c}{\displaystyle \left(x_1+2\right)\left(x_2+2\right)=x_1{x}_2+2\left(x_1+x_2\right)+4=b-2c+4=c\mathrm{.}}\end{array}$ A $b=c-4$ és a $b=3c-4$ egyenletekből álló egyenletrendszer megoldása: $b=-4$, $c=0$. $b)$ Mivel $x_1=6$ és $x_2=D=b^2-4c$, azért $\begin{array}{c}{\displaystyle x_1+x_2=6+b^2-4c=-b\text{és}{x}_1{x}_2=6\left(b^2-4c\right)=c\mathrm{.}}\end{array}$ A $b^2+b-4c+6=0$ és a $6b^2-25c=0$ egyenletekből álló egyenletrendszer megoldása: $b_1=-10$, $c_1=24$ és $b_2=-15$, $c_2=54$. $c)$ Mivel $x_1+x_2=-b$ és $x_1{x}_2=c$, azért $x_1^2{x}_2+x_1{x}_2^2=x_1{x}_2\left(x_1+x_2\right)=-cb$ és $\begin{array}{c}{\displaystyle x_1^3+x_2^3={\left(x_1+x_2\right)}^3-3x_1{x}_2\left(x_1+x_2\right)=-b^3+3cb\mathrm{.}}\end{array}$ A keresett polinom szorzat alakban: $\left(x+b\right)\left(x+cb\right)\left(x+b^3-3cb\right)$. Elvégezve a beszorzást: $\begin{array}{c}{\displaystyle x^3+b\left(b^2-2c+1\right)x^2+b^2\left(b^2+b^{2}c-3c^2-2c\right)x+b^{3}c\left(b^2-3c\right)\mathrm{.}}\end{array}$   6. Oldjuk meg a $\left(4-\text{cos}8x\right)\left(2+\text{cos}2x\right)=15$ egyenletet.  (16 pont)   Megoldás. Vizsgáljuk meg a szorzat tényezőinek lehetséges értékeit. Mivel a koszinuszfüggvény értékkészlete $\left[-1;1\right]$, azért $3\le 4-\text{cos}8x\le 5$ és $1\le 2+\text{cos}2x\le 3$. A szorzat csak akkor egyenlő 15-tel, ha mindkét tényező maximális. Így a következő két egyenlet közös gyökeit keressük: $4-\text{cos}8x=5$ és $2+\text{cos}2x=3$, azaz $\text{cos}8x=-1$ és $\text{cos}2x=1$. Az elsőből: $\begin{array}{c}{\displaystyle x_1=\frac{\pi }{8}+k_1\cdot \frac{\pi }{4}\mathrm{,}\text{ahol}{k}_1\in \text{Z}\mathrm{,}}\end{array}$ a másodikból: $x_2=k_2\cdot \pi$, ahol $k_2\in \text{Z}$. A kapott $x_1$ és $x_2$ értékek között nincs közös, ezért az eredeti egyenletnek nincs valós megoldása.   7. $a)$ Egy $27$ fős osztályba $5$-tel több lány jár, mint fiú. Mekkora a valószínűsége, hogy véletlenszerűen kiválasztott három tanuló között két fiú és egy lány van? $b)$ Egy $27$ fős osztályból kiválasztunk két tanulót. Határozzuk meg az osztályban a fiúk számát úgy, hogy a legnagyobb valószínűsége legyen annak, hogy a kiválasztott tanulók különböző neműek. Mekkora ez a maximális valószínűség? $c)$ A $27$ fős $11$. osztályban egy rosszul sikerült matematika dolgozat átlaga pontosan $2$. Az $5$-ös, $4$-es, $3$-as osztályzatok száma egyenlő és azt is tudjuk, hogy valamennyi érdemjegy előfordult. Mennyi lehet az osztályzatok módusza és a mediánja?  (16 pont)   Megoldás. $a)$ Három tanulót $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{27}{3}\right)=\frac{27\cdot 26\cdot 25}{1\cdot 2\cdot 3}=2925\text{-féleképpen}}\end{array}$ tudunk kiválasztani az osztályból. Az osztályba 16 lány és 11 fiú jár. A 11 fiúból $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{11}{2}\right)=\frac{11\cdot 10}{1\cdot 2}=55\text{-féleképpen}}\end{array}$ választhatunk ki kettőt. Mindegyik kiválasztáshoz tartozhat a 16 lány bármelyike, vagyis a kedvező esetek száma $16\cdot 55=880$. A keresett valószínűség: $\frac{880}{2925}\approx 0\mathrm{,}3$. $b)$ Ha a fiúk számát $n$-nel jelöljük, akkor a lányok száma $27-n$. Az összes eset $\frac{27\cdot 26}{2}=351$, a kedvező esetek száma: $\begin{array}{c}{\displaystyle n\left(27-n\right)=-{\left(n-13\mathrm{,}5\right)}^2+182\mathrm{,}25.}\end{array}$ Ez $n=13\mathrm{,}5$ esetén lenne maximális. Mivel $n$ egész szám, azért a kedvező esetek száma akkor maximális, ha $n=13$ vagy $n=14$. Vagyis 13 fiú és 14 lány, illetve 14 fiú és 13 lány esetén a legnagyobb a valószínűsége annak, hogy 1 fiút és 1 lányt választottunk. Ez a valószínűség: $\begin{array}{c}{\displaystyle \text{P}\left(\text{1 fiú}\mathrm{,}\text{1 lány}\right)=\frac{13\cdot 14}{351}=\frac{14}{27}\approx 0\mathrm{,}52.}\end{array}$ $c)$ A feltételek alapján legyen $a$ db elégtelen, $b$ db elégséges, $c$ db közepes, jó és jeles. Ekkor $\begin{array}{c}{\displaystyle a+b+3c=27\text{és}\frac{a+2b+c\left(3+4+5\right)}{27}=2.}\end{array}$ A második egyenletet alakítjuk: $a+2b+12c=54$. A két egyenletből a $c$-t kiejtjük, ezután: $a=18-\frac{2b}{3}$. A $b$ lehetséges értékeihez kiszámoljuk az $a$-t és a $c$-t: ${\displaystyle \begin{array}{ccccccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>b</mi></math>}}\hfill & \hfill {\displaystyle \text{3}}& \hfill {\displaystyle \text{6}}& \hfill {\displaystyle \text{9}}& \hfill {\displaystyle \text{12}}& \hfill {\displaystyle \text{15}}& \hfill {\displaystyle \text{18}}& \hfill {\displaystyle \text{21}}& \hfill {\displaystyle \text{24 }}\\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi></math>}}\hfill & \hfill {\displaystyle \text{16}}& \hfill {\displaystyle \text{14}}& \hfill {\displaystyle \text{12}}& \hfill {\displaystyle \text{10}}& \hfill {\displaystyle \text{8}}& \hfill {\displaystyle \text{6}}& \hfill {\displaystyle \text{4}}& \hfill {\displaystyle \text{2 }}\\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>c</mi></math>}}\hfill & \hfill {\displaystyle \text{‐}}& \hfill {\displaystyle \text{‐}}& \hfill {\displaystyle \text{2}}& \hfill {\displaystyle \text{‐}}& \hfill {\displaystyle \text{‐}}& \hfill {\displaystyle \text{1}}& \hfill {\displaystyle \text{‐}}& \hfill {\displaystyle \text{‐ }}\end{array}}$ A $c$ csak két esetben lett egész, ezek a számhármasok minden feltételnek megfelelnek. ${\displaystyle \begin{array}{ccccccc}{\displaystyle }\hfill & \hfill {\displaystyle \text{1-es}}\hfill & \hfill {\displaystyle \text{2-es}}\hfill & \hfill {\displaystyle \text{3-as}}\hfill & \hfill {\displaystyle \text{4-es}}\hfill & \hfill {\displaystyle \text{5-ös}}\hfill & {\displaystyle }\hfill \\ {\displaystyle \text{ 1. eset (db)}}\hfill & \hfill {\displaystyle \text{12}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>9}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{2}}\hfill & {\displaystyle \text{Ekkor a módusz: 1, a medián: 2.}}\hfill \\ {\displaystyle \text{ 2. eset (db)}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn></mphantom></math>6}}\hfill & \hfill {\displaystyle \text{18}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{1}}\hfill & {\displaystyle \text{Ekkor a módusz: 2, a medián: 2.}}\hfill \end{array}}$   8. Egy harmadfokú $f\left(x\right)$ függvényről tudjuk, hogy $f\left(1\right)=f\left(3\right)=4$, a harmadfokú tag együtthatója $1$, továbbá ${\int }_1^{5}f\left(x\right)dx=16$. Írjuk fel a függvénygörbe érintőjének egyenletét a $4$ abszcisszájú pontjában.  (16 pont)   Megoldás. A harmadfokú függvény hozzárendelési szabálya: $\begin{array}{c}{\displaystyle f\left(x\right)=x^3+b{x}^2+cx+d\mathrm{.}}\end{array}$ Tudjuk, hogy: $f\left(1\right)=1+b+c+d=4$, $f\left(3\right)=27+9b+3c+d=4$, továbbá: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\int }_1^{5}f\left(x\right)dx}& {\displaystyle ={\int }_1^5\left(x^3+b{x}^2+cx+d\right)dx={\left[\frac{x^4}{4}+b\cdot \frac{x^3}{3}+c\cdot \frac{x^2}{2}+d\cdot x\right]}_1^5=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{625}{4}+b\cdot \frac{125}{3}+c\cdot \frac{25}{2}+5d-\frac{1}{4}-b\cdot \frac{1}{3}-c\cdot \frac{1}{2}-d}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{124}{3}b+12c+4d+156=16.}\hfill \end{array}}$ A kapott három egyenlet rendezése után a következő egyenletrendszert kapjuk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cccc}\hfill {\displaystyle b+}& \hfill {\displaystyle c+}& \hfill {\displaystyle d}& {\displaystyle =3}\hfill \\ \hfill {\displaystyle 9b+}& \hfill {\displaystyle 3c+}& \hfill {\displaystyle d}& {\displaystyle =-23}\hfill \\ \hfill {\displaystyle 31b+}& \hfill {\displaystyle 9c+}& \hfill {\displaystyle 3d}& {\displaystyle =-105.}\hfill \end{array}}\}}\end{array}$ Az egyenletrendszer megoldása: $b=-9$, $c=23$, $d=-11$, azaz a harmadfokú függvény hozzárendelési szabálya: $f\left(x\right)=x^3-9x^2+23x-11$.     Meghatározzuk a keresett érintő meredekségét. Mivel $f\text{'}\left(x\right)=3x^2-18x+23$, így $f\text{'}\left(4\right)=3\cdot 4^2-18\cdot 4+23=-1$. Az érintő meredeksége: $m=-1$. Mivel $f\left(4\right)=4^3-9\cdot 4^2+23\cdot 4-11=1$, azért az érintési pont koordinátái: $E\left(4;1\right)$. Az $E\left(4;1\right)$ pontra illeszkedő, $m=-1$ meredekségű érintő egyenlete: $x+y=5$.   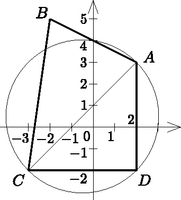9. Adottak az $ABCD$ konvex négyszög három csúcsának koordinátái: $A\left(2;3\right)$, $B\left(-2;5\right)$, $C\left(-3;-2\right)$, továbbá a $D$ csúcsnál lévő belső szöge, ami ${90}^{\circ }$. $a)$ Számítsuk ki az $ABC$ háromszög területét. $b)$ Határozzuk meg a $D$ csúcs koordinátáit úgy, hogy az $ABCD$ négyszög területe maximális legyen. 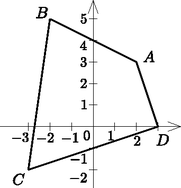$c)$ Mekkora az $ABCD$ négyszög kerülete, ha a $D$ pont illeszkedik az $x$ tengelyre?  (16 pont)   Megoldás. $a)$ Az $AC$ átló hossza $5\sqrt[]{2}$, a $B$ csúcs távolsága az $AC$ egyenestől $3\sqrt[]{2}$ egység. Innen az $ABC$ háromszög területe: $\frac{5\sqrt[]{2}\cdot 3\sqrt[]{2}}{2}=15$ területegység.     $b)$ Az $ABC$ háromszög területe nem változik, ezért a $D$ csúcsot úgy kell meghatároznunk, hogy az $ACD$ derékszögű háromszög területe maximális legyen. Mivel $AC$ adott, azért a $D$ távolsága az $AC$-től maximális kell, hogy legyen. A $D$ pont illeszkedik az $AC$ Thalész-körére, és az előzőek alapján illeszkednie kell az $AC$ felező merőlegesére is. Ennek egyenlete: $y+x=0$. Az egyenes megfelelő metszéspontja a Thalész-körrel: $D\left(2;-2\right)$.     $c)$ Legyen az $x$ tengelyre illeszkedő, a feladat feltételeinek megfelelő pont: $D\left(d;0\right)$. Ekkor $A{D}^2={\left(d-2\right)}^2+9$, $C{D}^2={\left(d+3\right)}^2+4$. Mivel az $ACD$ háromszög derékszögű, azért Pitagorasz-tétele szerint: ${\left(d-2\right)}^2+9+{\left(d+3\right)}^2+4=50$. A rendezés után a $d^2+d-12=0$ egyenletet kapjuk. Ennek csak a $d=3$ megoldása lesz megfelelő. A $D\left(3;0\right)$ koordinátájú pont a feladat feltételeit teljesíti. Az így kapott $ABCD$ konvex négyszög kerülete: $\begin{array}{c}{\displaystyle AB+BC+CD+DA=2\sqrt[]{5}+5\sqrt[]{2}+2\sqrt[]{10}+\sqrt[]{10}\approx 21\text{ (egység).}}\end{array}$