Cím: Latin négyzetek I.
Szerző(k):  Dénes Tamás 
Füzet: 2005/április, 194 - 199. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nem egyedülálló a matematika történetében, hogy egyes fejezetei a szórakozás, a játék területén fogantak és hosszabb-rövidebb fejlődés után a matematika új fejezeteivé váltak. Ezt az utat járta be a kombinatorika egy ,,alig'' 300 éves fejezete, a latin négyzetek elmélete. Különössége mégsem abban áll, hogy fejlődésének és főleg alkalmazásainak jelentős része a XX. század gyümölcse, hanem abban, hogy a klasszikus numerikus gondolkodást felcserélte a struktúrák belső összefüggéseinek elemzésével és ugyanakkor szemléletes ábrázolásával1.

 
Alapfogalmak és definíciók
 

Mivel a latin négyzetek elmélete egyelőre nem képezi matematika oktatásunk törzsanyagát, így a jelen dolgozat megértéséhez az olvasónak néhány alapfogalom megismerésére lesz szüksége.
Egy n-ed rendű latin négyzeten olyan n×n méretű négyzetes táblázatot (mátrixot) értünk, amelynek soraiban és oszlopaiban az a1,a2,...,an elemek mindegyike pontosan egyszer szerepel. Legyenek ezek az a1,a2,...,an elemek például az 1,2,...,n természetes számok. Az 1/a., 1/b. ábra példát mutat egy-egy 4-ed rendű latin négyzetre.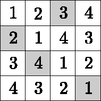
 

 
1/a. ábra
 

 
1/b. ábra
 

A definícióból világosan kiderül, hogy jelen esetben az a1,a2,...,an elemek számértéke közömbös, csupán az számít, hogy a táblázat egyes mezőiben álló elemek közül melyek egyenlők, illetve különbözők.
Egy latin négyzetet ciklikusnak nevezünk, ha egymás alatti soraiban az elemek sorrendje azonos, csak egy hellyel jobbra (vagy balra) vannak az elemek eltolva (lásd 1/b. ábra).
Egy n-ed rendű latin négyzet egy tranzverzálisán olyan n darab különböző elemét értjük, amelyek más-más sorban, illetve oszlopban helyezkednek el. Az 1/a. ábrán látható latin négyzetben a satírozott négy elem például tranzverzálist alkot.
Két n-ed rendű latin négyzetet akkor nevezünk ortogonálisnak, ha egymásra helyezve őket, az egymás felett levő elemekből alkotott párok mind különbözőek. Példaképpen bemutatjuk az 1/a. ábrán szereplő latin négyzet egy ortogonális párját (lásd 2. ábra), majd a két latin négyzet egymásra helyezésével nyert számpárokat. (Az olvasó a 3. ábra segítségével könnyen meggyőződhet arról, hogy a 16 számpár mind különböző.)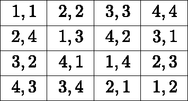
 

 
2. ábra
 


 
3. ábra
 

Az ortogonális latin négyzet párok létezése, mint látni fogjuk, szoros kapcsolatban van a tranzverzálisokkal. Erre vonatkozó alapvető eredmény Dulmage és Mendelsohn tétele:
 
Két n-ed rendű latin négyzet ortogonalitásának szükséges és elégséges feltétele, hogy a diszjunkt diagonálisaik száma pontosan n legyen.
 

Az n-ed rendű L1,L2,...,Lk latin négyzetek ortogonális rendszert alkotnak, ha közülük bármely két különböző ortogonális párt képez. Belátható, hogy n×n-es latin négyzetekből legfeljebb n-1 olyan létezhet, amelyek közül bármely kettő ortogonális; ha létezik n-1, akkor ortogonális latin négyzetek teljes rendszeréről beszélünk. A XX. század elején kiderült, hogy számos súlyos kombinatorikai probléma mélyén az ilyen rendszerek létezésének kérdése rejlik.
Egy L latin négyzetet akkor nevezünk vízszintesen teljesnek, ha a latin négyzetben szereplő bármely a, b (a≠b) elempárra van olyan sora L-nek, amelyben az a elemet b követi. (Ha a leírt tulajdonság oszlop irányban teljesül, akkor az L latin négyzetet függőlegesen teljesnek nevezzük.) Egy latin négyzetet, amely vízszintesen és függőlegesen is teljes, teljes latin négyzetnek hívunk. A 4. ábrán látható egy példa teljes latin négyzetre.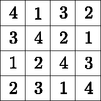
 

 
4. ábra

 
Kártyalapok és a 36 tiszt problémája
 

Leonhard Euler (1707‐1783), a XVIII. századi matematika óriása a latin négyzetek névadója, mivel ő alkalmazott a négyzetes mátrixbeli elemek jelölésére latin betűket, az addig szokásos számok helyett. Ez az algebrai struktúrák területén hasonló jelentőséggel bírt, mint F. Viéte (1540‐1603) 200 évvel korábbi tette, az algebrai egyenletek szimbólumainak bevezetésével. Eulert szokták említeni, mint aki bevezette az ortogonális latin négyzet párok fogalmát is. Azonban már Eulert megelőzően is ismerték az Eulernek tulajdonított két fogalmat. Claude-Gaspar Bachet de Méziriac (1581‐1638) és M. Ozanam (1640‐1712) már Euler előtt is játékkártyával kapcsolatosan jutottak a latin négyzetek, illetve ezekből alkotott ortogonális párok fogalmához (lásd [1], [4]). Tőlük való az 5. ábrán látható negyedrendű ortogonális latin négyzet pár, amely tulajdonképpen a következő feladatot oldja meg: hogyan lehet a francia kártya négy színű (kőr, treff, káró, pikk) figuráit (ász, király, dáma, bubi) egy 4×4-es táblázatban úgy elrendezni, hogy minden sorban, illetve oszlopban minden szín és minden figura pontosan egyszer forduljon elő.
 

 
5. ábra
 

Később 1776-ban, majd 1779-ben Euler a Szentpétervári Akadémián tartott előadásában már megmutatta, hogy ha n 4-gyel osztható természetes szám, akkor létezik n-ed rendű latin négyzetekből álló ortogonális pár. Ugyancsak ekkor vetette fel az azóta 36 tiszt problémájaként ismert feladatot: Válasszunk ki 36 tisztet úgy, hogy közöttük hat különböző rendfokozatú szerepeljen és a tisztek hat különböző csapattestből kerüljenek kiválasztásra, minden egyes csapattestből hat különböző rendfokozatú tiszt szerepeljen a 36 között. Fel lehet-e a fentiek szerint kiválasztott tiszteket úgy állítani egy 6×6-os alakzatba, hogy minden egyes sorban, illetve oszlopban minden rendfokozat, illetve csapattest pontosan egyszer szerepeljen? A kérdés röviden úgy is feltehető, hogy létezik-e két olyan hatodrendű latin négyzet, amely egymásra ortogonális.
A feladat kísértetiesen hasonlít az előzőkben kártyákkal megoldottakhoz, mégis Euler azt sejtette, hogy a 36 tiszt problémájának nincs megoldása. Sőt, ennél általánosabban azt is sejtette, hogy ha n=4k+2 alakú, akkor nem létezik n-ed rendű ortogonális latin négyzet pár. Ez utóbbi sejtést évszázadokon át Euler-sejtésnek hívták, és több mint 200 évig megoldatlannak bizonyult.
 
Az Euler-sejtés cáfolata és néhány megoldatlan probléma
 

Már Euler tudta, hogy sejtése az n=2 esetre igaz (a bizonyítás igen egyszerű, hiszen az 1, 2 számokból mindössze két különböző 2×2-es latin négyzet készíthető). Az n=6 esetre, azaz a 36 tiszt problémájára a bizonyítással több mint 100 évet kellett várni, míg G. Tarry éppen a XX. század fordulóján, 1900-ban bebizonyította. Euler általános sejtése azonban nem bizonyult igaznak. Csaknem kétszáz évvel a sejtés megfogalmazása után, 1959-ben egy igen bonyolult bizonyítással R. C. Bose, S. S. Shrikhande és E. T. Parker megmutatta, hogy az Euler-sejtés semmilyen n≥10 esetén nem igaz, azaz minden n=4k+2 alakú számra ‐ ha k értéke legalább 2 ‐ léteznek n-edrendű ortogonális latin négyzetek.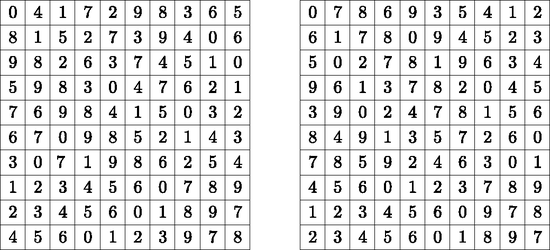
 

 
6. ábra
 

A 6. ábra szemlélteti azt a híres tizedrendű ortogonális latin négyzet párt, amelyet 1959-ben hoztak nyilvánosságra, megdöntve az Euler-sejtést az n=10 esetre.
Mint említettem, ismert tétel szerint egy n-ed rendű latin négyzetekből álló ortogonális rendszerben legfeljebb (n-1) latin négyzet lehet. Nagyon keveset tudunk arról, hogy ez a felső korlát mikor érhető el. Tudjuk, hogy ha n=pr prímhatvány, akkor van teljes n-ed rendű ortogonális rendszer. Az n=22 esetre példa a 7. ábrán látható három latin négyzetből álló negyedrendű ortogonális rendszer.
 

 
7. ábra
 

Mindeddig nem sikerült azonban n-ed rendű latin négyzetekből álló teljes ortogonális rendszert találni, ha n nem prímhatvány. R. H. Bruck és H. J. Ryser bebizonyították a következő tételt: n-ed rendű latin négyzetekből álló teljes ortogonális rendszer nem létezik, ha n≡1 vagy 2(mod4) (azaz n a 4-gyel osztva 1 vagy 2 maradékot ad), kivéve, ha n=a2+b2 alakú (azaz n két négyzetszám összegeként előállítható). Itt érdemes megjegyezni, hogy Fermat híres karácsonyi tétele (melyet 1640 karácsonyán egy M. Mersenne-nek írt levelében fogalmazott meg) így szól: Minden n=4k+1 alakú prímszám felírható két egész szám négyzetének összegeként. (E két tétel összevetéséből tehát a prímhatványok nagyon speciális eseteként következik, hogy ha n  4k+1 alakú prímszám, akkor létezik n-1 darab latin négyzetből álló, azaz teljes ortogonális rendszer.)
Ha n nem speciális (pl. prímhatvány) alakú szám, akkor az ortogonális rendszerek elemszámára egyelőre csak becslések vannak. Jelölje N(n)az n-ed rendű latin négyzetekből álló ortogonális rendszerekben lévő latin négyzetek maximális számát, ekkor az előbbiek szerint N(n)≤n-1. S. Chowle., Erdős Pál és E. G. Straus bizonyította, hogy ha n ,,elég nagy'', akkor
N(n)<n1913,
majd ezt megjavítva R. M. Wilsonnak sikerült igazolni, hogy nagy n értékekre N(n)≥n117-2 is teljesül.
Végül a latin négyzetekkel való barátkozáshoz bemutatok egy társasjátékot. A játékot két játékos játssza, A és B (mindig A teszi meg az első lépést). A játékot egy n×n méretű üres táblán játsszák. Kezdéskor A egy 1 és n közötti számot a tábla tetszés szerinti helyére ír, majd B úgy ír a tábla még üres mezőinek egyikére egy szintén 1 és n közötti számot, hogy az a latin négyzet tulajdonsággal ne ütközzön, azaz semelyik sorban és semelyik oszlopban ne álljon két egyenlő szám (az ilyen lépéseket legálisnak nevezzük). A játékosok felváltva lépnek; az nyer, aki utoljára tud legális lépést tenni.
4×4-es táblán a játék egy lehetséges lefolyását láthatjuk a 8. ábrán. A fehér mezőkre írt számok A, a szürke mezőkre írtak B lépéseit mutatják.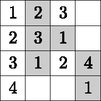
 

 
8. ábra
 

Mivel A kezdett, így 6 lépés után láthatjuk, hogy B nyert, mivel A-nak már nincs helyes lépése. Harary és Leary [3]-ban megmutatta, hogy páros n esetén B nyer, páratlan n-re pedig A.
 
Hivatkozások
 

[1]Claude-Gasper Bachet: Problémes plaisant et detectables (1612).
[2]J. Dénes, A. D. Keedwell: Latin squares and their applications, Academic Press (New York), Akadémiai Kiadó (Budapest), English Universities Press (London, 1974).
[3]F. Harary, T. Leary: Latin square achievement games, J. Recreational Math., 16 (1983/84), 241‐246.
[4]M. Ozanam: Recreations mathematique et physiques, Tome 1‐4. Paris (Claude Joubert, 1723).
1A latin négyzetekről a máig is egyetlen [2] összefoglaló monográfia pontosan harminc éve született. Talán éppen ennek a kötetnek is köszönhető, hogy azóta az alkalmazások széles körben terjedtek el.