Cím: Diákköri dolgozatok
Szerző(k):  Vanyó József 
Füzet: 2006/február, 110 - 115. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek, Holdak, Merev testek dinamikája

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az egyetemek, főiskolák hallgatói már a tanulmányaik kezdetén bekapcsolódhatnak a tudományos diákköri kutatómunkába; eredményeiket diákköri konferencián ismertetik és értékelik. A középiskolás ,,nagyközönség'' érdeklődésére is számot tartó munkák rövid összefoglalását alkalmanként a KöMaL is közölni fogja. Az alábbi dolgozat, amely a szerzőnek az ELTE Elméleti Fizika Tanszékén Tél Tamás professzor irányítása mellett végzett munkájáról számol be, 2005-ben az Országos Tudományos Diákköri Konferencián I. díjat nyert.

 

Égitestek forgása a Naprendszerben
 

 
Bevezetés
 

Az emberiség már az ókorban törekedett arra, hogy az égbolton látható változásokat megértse, előre jelezze. A középkorban Johannes Kepler, Isaac Newton és sok más természettudós munkássága nyomán felcsillant a remény, hogy beteljesíthetjük az ősi törekvéseket. A XIX. század második felében élt Jules Henri Poincaré bebizonyította, hogy sosem leszünk képesek a bolygók mozgását tetszőlegesen hosszú időre előre meghatározni. Ennek ellenére az 1970-es évek végéig fennmaradt annak illúziója, hogy legalább néhány emberöltőnyi időre előre jelezhetjük a Naprendszer állapotát. Az illúziót egy olyan jelenség megfigyelése döntötte romba, amely a modern technika nélkül nem került volna látóterünkbe.
 
A Szaturnusz Hyperion nevű holdja
 

1981-ben a Voyager 1 űrszonda a Szaturnusz rendszerében egy igen érdekesen viselkedő holdat figyelt meg, a Hyperiont. A hold fényességváltozásából arra lehetett következtetni, hogy forgása egyáltalán nem szabályos. Részletesebb vizsgálatok kiderítették, hogy a Hyperion elég szabálytalan alakú (mérete: 410 km  ×260 km  ×220 km), és a Szaturnusz körüli pályája viszonylag nagy excentricitású (lapultságú). A további megfigyelések során fény derült a hold össze-vissza bugdácsoló, kaotikus forgására. Ennek a forgó mozgásnak az volt az igazán meglepő, zavarba ejtő tulajdonsága, hogy akárhogy is próbálták ‐ már a hold adatainak ismeretében ‐ előre jelezni, rövid időn belül (1‐2 hét) a megfigyelt mozgás már nem is hasonlított az előre kiszámítotthoz. Felmerül a kérdés: miért nem forog a Hyperion egy adott tengely körül egyenletesen úgy, mint a többi ,,normális'', addig megfigyelt égitest? Az előre jelezhetetlenségre és a kaotikus mozgásra Jack Wisdom adott magyarázatot 1987-ben.
Tekintsük az 1. ábrát. Ezen a legegyszerűbb szabálytalan alakú (nem gömbszimmetrikus) holdat (annak modelljét) ábrázoltuk, ami nem más, mint két tömegpont összekötve egy súlytalan rúddal. (A méretarányokat erősen eltorzítottuk; a valóságban a hold mérete sokkal kisebb, mint a vonzócentrumtól mért távolsága.) Az ábrán a hold felső 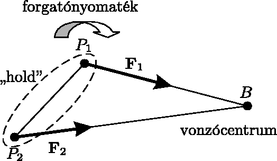P1 tömegpontja közelebb van a B bolygóhoz (vonzócentrum) mint az alsó P2 tömegpont, így P1-re nagyobb gravitációs erő hat, mint P2-re. A két erő eltérő nagyságának következménye, hogy az ábrázolt helyzetben a holdra az óramutató járásával megegyező irányú forgatónyomaték hat. Nem nehéz belátni, hogy egy tetszőleges alakú holdra is hat forgatónyomaték, ha az nem gömbszimmetrikus (gömbszimmetria esetén a forgatónyomatékok ,,semlegesítik'' egymást). A forgatónyomaték nagysága a hold alakján kívül a bolygó és a hold távolságától, valamint azok relatív helyzetétől függ.
 
 

1. ábra
 

Wisdom a kaotikus forgás magyarázatára felállított modelljében csak a Szaturnusz forgató hatását vette figyelembe, a Naprendszer többi tagjának forgató hatása ugyanis a nagy távolság miatt elhanyagolható. A Hyperion a Szaturnusz körül ellipszis alakú, periodikus pályán kering, tehát a holdat érő hatás valamilyen értelemben periodikus. A rendszerről kimutatható volt, hogy igen érzékeny a kezdőfeltételekre. Ez azt jelenti, hogy kiszámítva a hold forgását két, egymástól csak egy hajszálnyival eltérő kezdeti forgási állapotra, a jövőbeli mozgások igen rövid idő múlva gyökeresen eltérnek egymástól. A modell alapján ez a rövid idő napokban, hetekben mérhető. Ezek alapján érthető, hogy miért nem tudjuk a hold forgását előre meghatározni. A forgási állapotot ugyanis egzaktul, hiba nélkül nem lehet megmérni, s így a számítások nem a valóságos, hanem attól kissé eltérő kezdeti állapotra vonatkoznak.
A mozgás másik jellemzője az ,,összevisszaság'': közelítőleg sem ismétli önmagát, nem is periodikus, még csak nem is ún. kváziperiodikus. Ez a tulajdonság is meglepő, hiszen amióta az ember az eget figyeli, a látottakat periodikus vagy közel periodikus mozgásokkal tudta leírni.
A kaotikus jelenségeknek a fenti két tulajdonság alapfeltétele. Következtetésként megállapíthatjuk, hogy a kaotikusság az égitestek forgásában is megjelenhet, még akkor is, ha az égitestet érő forgató hatás periodikus. Az azonban nem igaz, hogy mindig meg is jelenik a káosz! Előfordulhat olyan kiindulási helyzet, hogy periodikus hatás következtében a forgás periodikus vagy kváziperiodikus lesz. A forgás szabályosságának, vagy kaotikus voltának eldöntéséhez igen jól kidolgozott módszer áll rendelkezésre: a stroboszkópikus metszetek módszere. Erre a későbbiekben még visszatérünk.
 
A Mars és a Föld forgásának vizsgálata
 

A fentiek tükrében fel kell tennünk a kérdést: mi a helyzet a Naprendszer többi égitestével, a bolygókkal, a holdakkal és elsősorban a Földdel? Tudjuk ugyanis, hogy ezek sem gömbszimmetrikusak (többségük forgási tengelyük mentén lapított). Szabálytalanságuk jóval kisebb mértékű, azonban egymásra is képesek forgatónyomatékkal hatni és így az őket érő hatások nem periodikusak, hanem annál jóval bonyolultabbak. Tehát nem lenne meglepő, ha találnánk más olyan égitestet is, amelynek forgása a megszokott értelemben szintén nem ,,szép''.
A kérdést Jacques Laskar és Philippe Robutel tanulmányozta először. Legérdekesebb eredményük, hogy a Mars bolygó forgástengelyének irányváltozása jelenleg is kaotikus. A forgástengely iránya a pályasíkra merőleges 0∘-os dőlésszögétől 60∘-ig változhat. Lényeges azonban megemlíteni, hogy a Mars kaotikus forgása csak néhány évmilliárd alatt nyilvánul meg, a mi életünkben a Mars nem fog a maitól lényegesen eltérő tengely körül forogni. A múltban azonban a forgástengely irányváltozása igen komoly hatással lehetett a Mars éghajlatának változásaira. Ennek geológiai lenyomatait vélik napjainkban felfedezni a Marsot kutató űrszondák.
Szerencsére a Föld esetén nem ekkora mértékű a forgástengely irányváltozása ‐ a számítások szerint nem nagyobb 1,3∘-nál. A részletesebb számítások azt is kimutatták, hogy a Hold jelenléte nélkül a Föld is a Marshoz hasonló mértékben változtatná a forgástengelyének irányát, azaz a Hold mindegy megvédi a Földet az ilyen nagymértékű változásoktól, és így fontos szerepe van a Föld forgásának stabilizálásában.
 
A legveszélyesebb kisbolygó
 

A napjainkban nyilvántartott kisbolygók közül a Földet leginkább az 1950 DA nevezetű fenyegeti. Annak valószínűsége, hogy a Földbe csapódik: 0,33%. Az olvasó erre mondhatja, hogy ez nem túl jelentős, hiszen a katasztrófa valószínűsége ,,csupán'' 1:300. Gondoljuk meg azonban, hogy mi forog kockán, s így mindjárt nem tűnik olyan kicsinek ez a valószínűség.
Annak oka, hogy ez a valószínűség ilyen nagynak adódott elsősorban az, hogy nem tudunk semmit a kisbolygó forgásáról. A forgás a kisbolygók esetében jelentős hatással lehet a pályára. Ha nem ismerjük a forgási állapotot, az bizonytalanságot okoz a kisbolygó pályájának meghatározásakor. Ha ismernénk a forgást, akkor elképzelhető, hogy az ütközést esetleg teljesen kizárhatnánk, vagy megbizonyosodhatnánk annak bekövetkeztéről, és így megtehetnénk a megfelelő lépéseket a katasztrófa elkerülése érdekében.
A forgás meghatározása ebben az esetben bonyolultabb, mint a Hyperionnál, mivel az aszteroida forgását nem csak egy bolygó befolyásolja. A bevezetőben említettük, hogy Poincaré bebizonyította az égitestek tömegközéppontjának kaotikus mozgását a Naprendszerben. A forgásállapot gerjesztését a kisbolygónak a többi égitesthez viszonyított helyzete, mozgása határozza meg. Ennek következménye, hogy a forgató hatás, azaz a gerjesztés sem periodikus, hanem annál bonyolultabb: kaotikus.
Azzal a problémával találjuk tehát szembe magunkat, hogy egy olyan rendszer kaotikus gerjesztésre való válaszát kellene meghatároznunk, ami már periodikus gerjesztésre is kaotikusan reagál.
Megnyugtatásul közlöm az olvasóval, hogy a szóbanforgó esemény ‐ az aszteroida becsapódása ‐ 878 év múlva esedékes. Az előzőek azonban rávilágítanak a forgásállapot ismeretének jelentőségére a Naprendszer ,,parányibb'' tagjainak körében is.
 
Forgás a síkbeli kör korlátozott háromtest-problémában
 

Annak ellenére, hogy a naprendszerbeli nagyobb égitestek forgását mennyiségileg már igen részletesen tanulmányozták, a forgás szisztematikus minőségi vizsgálata a mai napig nem történt meg. Elképzelhetőek olyan törvényszerűségek, amelyek rejtve maradnak a kvantitatív vizsgálatok mögött. Ha ismereteink lennének ezekről a törvényekről, azzal a megfigyelt jelenségek nagyobb körét tudnánk megmagyarázni, megérteni, és esetleg a már meglévő eredmények újabb értelmezésére is sort keríthetnénk. A tudománynak nem csak az a feladata, hogy képes legyen mennyiségi jóslatokat tenni, hanem az is, hogy a jelenségek magyarázatát megadja ‐ hiszen előzőleg épp olyan rendszerre láttunk példát, ahol a mennyiségi előrejelzés nemhogy nem lehetséges, de nincs is értelme neki.
A Naprendszerről ‐ annak bonyolultsága miatt ‐ igen nehéz minőségi megállapításokat tenni, ezért úgy járunk el, hogy a probléma bonyolultságát csökkentjük, de alaptermészetét megtartjuk. A Naprendszerben bármely nem gömbszimmetrikus testre általában kaotikus forgatónyomaték hat. Ezért azt a legegyszerűbb rendszert vizsgáljuk, amiben még előfordul kaotikus forgató hatás, de benne a lehető legkevesebb égitest szerepel. Ebben az egyszerűbb rendszerben próbálunk meg törvényeket felállítani, és ezek tükrében a bonyolultabb rendszerek vizsgálatát megismételjük.
A legegyszerűbb ilyen rendszer a következő: tekintsünk két ‐ egymás körül körpályán keringő ‐ pontszerű égitestet, és egy harmadikat, melynek tömege a másik kettőhöz viszonyítva elhanyagolható. Feltesszük, hogy a három égitest egy síkban mozog. Ez az úgynevezett síkbeli kör korlátozott háromtest-probléma. Az elhanyagolható tömegű égitestet kiterjedtnek tételezzük fel, és ennek forgását tanulmányozzuk. Ha a kiterjedtnek tekintett test nem gömbszimmetrikus, akkor a másik két test forgatónyomatékkal hat rá. A forgás szempontjából ez egy gerjesztett rendszer. A forgás gerjesztésének minőségét az határozza meg, hogy milyen a harmadik égitest mozgása a másik kettőhöz viszonyítva. A 2. ábrán a kis test egy kaotikus pályáját ábrázoltuk a két nagy égitesthez rögzített koordináta-rendszerben. (Az inerciarendszerből szemlélve mindhárom égitest még az 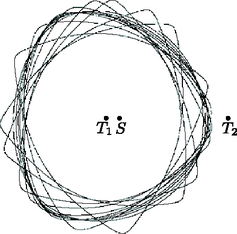S tömegközéppont körül is körbeforog.) Ha a kis égitest tömegközéppontja ezen a pályán mozog, akkor a rá ható forgatónyomaték is kaotikus lesz. Azonban ebben a rendszerben kivételes esetekben az is megeshet, hogy a kis test tömegközéppontja periodikus, vagy kváziperiodikus pályán mozog, s ekkor a gerjesztés minősége is hasonló lesz. Kiválasztott rendszerünk tehát hidat képez a Naprendszer és a ‐ stroboszkópikus metszetek módszerével vizsgálható ‐ Hyperion-probléma között.
 
 

2. ábra
 

Periodikus pályák esetén a forgás jellemezhető az ún. stroboszkópikus térkép segítségével. Egy ilyen térkép látható a hátsó borító jobb felső ábráján. Ez az ábra valójában egy koordináta-rendszer, melynek minden pontja megfelel egy forgási állapotnak. A vízszintes koordináta a test helyzetét (a két nagy testet összekötő egyenes irányához viszonyított szöget), míg a függőleges koordináta a szögsebességet mutatja. Az ábra segítségével a forgás minősége egyértelműen meghatározható, ha ismerjük a kezdeti forgási állapotot. A forgás kaotikus lesz, ha a kezdeti állapotnak megfelelő pont a nagy kiterjedésű feketén pontozott tartományba (kaotikus sáv) esik. Kváziperiodikus forgás esetén egy színes vonalra, vagy egy zárt görbére ‐ ún. ,,szigetre'' ‐ esik a pont, míg ha egy ,,sziget'' belsejében lévő pontnak felel meg a kezdeti állapot, akkor periodikus lesz a forgás.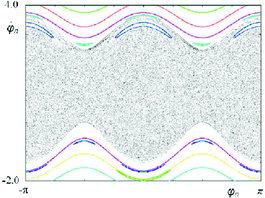
 

 
Egy kaotikusan forgó test mozgásának stroboszkopikus térképe
 

Sajnos a stroboszkópikus térkép kváziperiodikus és kaotikus pályák esetén elmosódik, elveszíti szerkezetét. Ez azzal kapcsolatos, hogy ezen gerjesztések esetén már csak kaotikus forgások lehetségesek. Ennél többet azonban a térkép segítségével nem mondhatunk, és mivel szerkezetét elveszítette, alkalmatlan a dinamika további jellemzésére.
 
A cseppmódszer
 

Új módszerre van tehát szükség, ennek neve: cseppmódszer. Az új módszer lényegének megértése előtt az alábbiakat kell meggondolnunk: a forgási állapot változásakor a test forgási állapotát reprezentáló pont vándorol a stroboszkópikus térkép koordináta-rendszerében, az ún. fázistérben. Ez a mozgás ahhoz hasonlítható, ahogyan egy áramlási térben a folyadék egy-egy részecskéje sodródik. Valójában ez a fázistér minden pontjára igaz, így az áramlások és a fázistérrel jellemzett rendszerek vizsgálata közt párhuzam vonható. Áramlásokat szokás úgy vizsgálni, hogy az áramló folyadékot egy helyen megfestik oly módon, hogy valahová egy, az áramló folyadék színétől eltérő színű folyadékot cseppentenek. Ezután a megfestett folyadék sodródásából, szétterjedéséből következtetnek az áramlás tulajdonságaira. A módszer segítségével tulajdonképpen nem mást teszünk, mint megjelöljük és szemmel követjük az áramló folyadék kezdetben egymás közelében elhelyezkedő sok-sok részecskéjét.
Lássuk, hogyan alkalmazható a cseppmódszer például a Hyperion-problémánál. Tegyük fel, hogy megmérjük a hold helyzetét, valamint a szögsebességét, és tisztában vagyunk azzal, hogy mérésünk mekkora hibát tartalmaz. A hibák miatt nem tudjuk meghatározni a hold állapotának megfelelő pontos fázistérbeli pontot, de meg tudunk határozni egy tartományt, ahol a pontnak lennie kell. Cseppmódszer segítségével ennek a tartománynak ‐ mint cseppnek ‐ a mozgását figyeljük. Ezzel a módszerrel nem tudjuk meghatározni a későbbi állapotot. Azt azonban meg tudjuk mondani, hogy egy későbbi időpontban bizonyos állapotban lehet-e a rendszer, vagy sem, s így mindjárt többet mondhatunk a rendszer jövőbeli viselkedéséről. Sőt, esetenként valószínűségi leírást is adhatunk arról, hogy milyen állapotnak mekkora valószínűsége lesz.
Ez a módszer változtatás nélkül átvihető kaotikusan gerjesztett mozgásokra is. A hátsó borító jobb alsó ábrája egy kaotikusan gerjesztett rendszerben sodródó csepp már meglehetősen szétterjedt állapotát mutatja. Itt a gerjesztést a 2. ábrán felrajzolt kaotikus pálya határozta meg. Jól megfigyelhető a csepp szálas szerkezete, ami a csepp megnyúlásának és sokszori összetekeredésének következménye.
 
 

Kaotikusan gerjesztett rendszer fázisterében sodródó csepp szétterjedt állapotban
 

A cseppmódszer segítségével még további módokon is vizsgálható egy rendszer viselkedése. Ezekre itt nem térünk ki, de megemlítjük, hogy kaotikus rendszerben az idő előrehaladtával a csepp mindinkább fraktáltulajdonságokkal rendelkezik. Ezek a tulajdonságok és maga a fraktál alakja szintén információkat hordoz a rendszer viselkedéséről.
Végezetül fontos kiemelni, hogy a cseppmódszer alkalmazása ígéretesnek tűnik minden bonyolult ‐ netán kaotikus ‐ hatások alatt lévő rendszer jellemzésére. Példaként említhetőek ‐ a fizikai rendszereken kívül ‐ az egymással összekapcsolódó biológiai és kémiai rendszerek, ahol szintén gyakran felüti fejét a káosz.