Kezdőlap


Cím:	A 2005. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldásai
Szerző(k):	Fleiner Tamás
Füzet:	2006/február, 68 - 73. oldal	PDF \| MathML
Témakör(ök):	Kürschák József (korábban Eötvös Loránd), Matematika, Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Legyen $N > 1$ és legyenek $a_{1}, a_{2}, ..., a_{N}$ olyan nemnegatív valós számok, amelyek összege legfeljebb $500$ . Bizonyítandó, hogy létezik olyan $k \geq 1$ egész szám és léteznek olyan $1 = n_{0} < n_{1} < ... < n_{k} = N$ egészek, amelyekre teljesül, hogy

\begin{matrix} \sum_{i = 1}^{k} n_{i} a_{n_{i - 1}} < 2005. \end{matrix}

(1)

I. megoldás. Osszuk az

(a_{n})

sorozatot blokkokra: a nulladik blokk álljon

a_{1}

-ből, az első legyen

a_{2}, a_{3}

, a másodikhoz tartozzon

a_{4}, ..., a_{7}

. Általában az

i

-dik blokk az

a_{2^{i}}

elemtől tartalmazza a sorozat elemeit az

a_{2^{i + 1} - 1}

elemmel bezárólag.

(Ha

2^{i + 1} - 1 > N

, akkor a blokk értelemszerűen csak

a_{N}

-ig tartalmazza a sorozat elemeit.) Tegyük fel, hogy

k + 1

blokkból áll az

(a_{n})

sorozat, vagyis az utolsó blokk a

k

-adik. Legyen

i < k

-ra

a_{n_{i}}

i

-edik blokk legkisebb eleme, és legyen

n_{k} = N

. A blokkok és az

n_{i}

-k megválasztása miatt

n_{i} < 2^{i + 1}

, ezért

\begin{matrix} n_{i} a_{n_{i - 1}} \leq 2^{i + 1} \cdot a_{n_{i - 1}} = 4 \cdot 2^{i - 1} a_{n_{i - 1}} \leq 4 \cdot (a_{2^{i - 1}} + ... + a_{2^{i} - 1}), \end{matrix}

ahol az utolsó egyenlőtlenség

a_{n_{i - 1}}

definíciójából és abból következik, hogy az

(i - 1)

-edik blokk éppen

2^{i - 1}

db elemet tartalmaz. Azt kaptuk tehát, hogy az

n_{i} a_{n_{i - 1}}

szorzat legfeljebb

4

-szerese az

(i - 1)

-edik blokkban álló elemek összegének, tehát e szorzatok összege is legfeljebb

4

-szerese az első

k

blokk összegének:

\begin{matrix} \sum_{i = 1}^{k} n_{i} a_{n_{i - 1}} < 4 \cdot \sum_{i = 1}^{2^{k} - 1} a_{i} \leq 4 \cdot \sum_{i = 1}^{N} a_{i} \leq 4 \cdot 500 < 2005. □ \end{matrix}

Több versenyző is próbálkozott a feladatban szereplő összeg lehetséges értékeinek átlagolásával. Ha ugyanis ez az átlag kisebb lenne

2005

-nél, az garantálná, hogy létezik a feltételt teljesítő sorozat. Másképpen fogalmazva: állítsuk elő az

n_{0}, ..., n_{k}

sorozatot véletlenszerűen úgy, hogy az

2,3, ..., N - 1

indexek mindegyikét (egymástól függetlenül)

\frac{1}{2}

valószínűséggel választjuk ki (a

0

-t és az

N

-et mindenképpen ki kell választanunk), és vizsgáljuk meg az így előállított

\sum n_{i} a_{n_{i - 1}}

véletlen összeg várható értékét. Ha a várható érték

2005

-nél kisebb, akkor ez biztosítja, hogy az állítás igaz.
Ez az ötlet ‐ ebben a formában ‐ nem vezethet eredményre, mert

\sum n_{i} a_{n_{i - 1}}

várható értéke tetszőlegesen nagy lehet. Az egyes indexek kiválasztási valószínűségének szerencsésebb megválasztásával azonban a feladat megoldható.

II. megoldás. Készítsük el az

n_{0}, ..., n_{k}

sorozatot véletlenszerűen úgy, hogy az

n

indexet tetszőleges

1 \leq n \leq N

esetén

p_{n}

valószínűséggel választjuk ki, és legyen az egyes indexek kiválasztása egymástól független.
A valószínűségeket a következőképpen válasszuk meg:

\begin{matrix} p_{n} = {\begin{matrix} \frac{2}{n + 1}, & ha 1 \leq n < N; \\ 1, & ha n = N . \end{matrix} \end{matrix}

Megjegyezzük, hogy az

1

és az

N

indexeket biztosan ki kell választanunk, ennek megfelelően

p_{1} = p_{N} = 1

.
Vizsgáljuk meg, hogy valamely

1 \leq n < m \leq N

esetén az

m a_{n}

kifejezés milyen valószínűséggel szerepel az (1) bal oldalán álló összeg tagjai között. Ennek szükséges és elégséges feltétele, hogy az

n

és

m

indexeket kiválasszuk, a közbülső indexek közül viszont egyet sem. Az

m a_{n}

tag előfordulásának valószínűsége tehát

\begin{matrix} p_{n} (1 - p_{n + 1}) \cdot ... \cdot (1 - p_{m - 1}) p_{m}, \end{matrix}

a teljes összeg várható értéke pedig

\begin{matrix} E (\sum_{i = 1}^{k} n_{i} a_{n_{i - 1}}) & = \sum_{1 \leq n < m \leq N} p_{n} (1 - p_{n + 1}) \cdot ... \cdot (1 - p_{m - 1}) p_{m} \cdot m a_{n} = & (2) \\ = \sum_{n = 1}^{N - 1} (\sum_{m = n + 1}^{N} p_{n} (1 - p_{n + 1}) \cdot ... \cdot (1 - p_{m - 1}) p_{m} \cdot m) a_{n} . \end{matrix}

m < N

, akkor

\begin{matrix} p_{n} (1 - p_{n + 1}) \cdot ... \cdot (1 - p_{m - 1}) p_{m} \cdot m = \\ = \frac{2}{n + 1} \cdot \frac{n}{n + 2} \cdot \frac{n + 1}{n + 3} \cdot ... \cdot \frac{m - 2}{m} \cdot \frac{2}{m + 1} \cdot m = \\ = \frac{4 n}{(m - 1) (m + 1)} < \frac{4 n}{(m - 1) m} = \frac{4 n}{m - 1} - \frac{4 n}{m} . \end{matrix}

Ha pedig

m = N

, akkor

\begin{matrix} p_{n} (1 - p_{n + 1}) \cdot ... \cdot (1 - p_{m - 1}) p_{m} \cdot m = \\ = \frac{2}{n + 1} \cdot \frac{n}{n + 2} \cdot \frac{n + 1}{n + 3} \cdot ... \cdot \frac{N - 2}{N} \cdot 1 \cdot N = \frac{2 n}{N - 1} . \end{matrix}

Ezeket a becsléseket beírva (2)-be,

\begin{matrix} \sum_{m = n + 1}^{N} p_{n} (1 - p_{n + 1}) \cdot ... \cdot (1 - p_{m - 1}) p_{m} \cdot m \leq \\ \leq \sum_{m = n + 1}^{N - 1} (\frac{4 n}{m - 1} - \frac{4 n}{m}) + \frac{2 n}{N - 1} = (\frac{4 n}{n} - \frac{4 n}{N - 1}) + \frac{2 n}{N - 1} < 4, \end{matrix}

és

\begin{matrix} E (\sum_{i = 1}^{k} n_{i} a_{n_{i - 1}}) < \sum_{n = 1}^{N - 1} 4 a_{n} \leq 4 \sum_{n = 1}^{N} a_{n} \leq 2000. \end{matrix}

Mivel a várható érték a lehetséges összegeknek a ‐ valószínűségük szerint ‐ súlyozott átlaga, a lehetséges összegek között biztosan létezik

2000

-nél kisebb.

□

2. feladat.

A

és

B

teniszeznek. Az a játékos győz, aki elsőként nyer meg legalább négy labdamenetet úgy, hogy ellenfelénél legalább kettővel több labdamenetet nyert. Tudjuk, hogy az

A

játékos minden labdamenetet, a korábbiaktól függetlenül,

p \leq \frac{1}{2}

valószínűséggel nyer meg. Bizonyítsuk be, hogy az

A

játékos győzelmének valószínűsége legfeljebb

2 p^{2}

I. megoldás. Legyen

A

mindazon játékok halmaza, amelyekben az

A

játékos nyer, míg a

B

halmaz tartalmazza a

B

által megnyert játékokat. Az

A

és

B

halmazok között kölcsönösen egyértelmű megfeleltetést hozunk létre, ha egy

A

által megnyert

G

játéknak az a

G'

játék lesz a párja, amiben minden labdamenetet épp a másik játékos nyer meg, mint ahogyan az

G

-ben történt. Azt mutatjuk meg, hogy tetszőleges

G \in A

játék esetén

\begin{matrix} P (G) \leq 2 p^{2} (P (G) + P (G')) . \end{matrix}

Ha ezt megtesszük, akkor

\begin{matrix} P (Anyer) & = \sum_{G \in A} P (G) \leq \sum_{G \in A} 2 p^{2} (P (G) + P (G')) = 2 p^{2} \sum_{G \in A} (P (G) + P (G')) = \\ = 2 p^{2} (\sum_{G \in A} P (G) + \sum_{G \in B} P (G)) = 2 p^{2} \cdot P (a játék véget ér) \leq 2 p^{2}, \end{matrix}

azaz bebizonyítottuk a feladat állítását.
Ha a

G

játékban

A

l

-szer és

B

k

-szor nyert labdamenetet, akkor abból, hogy a

B

játékos

q = 1 - p

valószínűséggel nyer meg egy labdamenetet kapjuk, hogy

P (G) = p^{l} \cdot q^{k}

, illetve

P (G') = p^{k} \cdot q^{l}

, továbbá a játék definíciója miatt

m : = l - k \geq 2

. Azt kell tehát igazolni, hogy

p^{l} \cdot q^{k} \leq 2 p^{2} (p^{l} \cdot q^{k} + p^{k} \cdot q^{l})

, ami azzal ekvivalens, hogy

p^{m} \leq 2 p^{2} (p^{m} + q^{m})

.
Világos, hogy

{(p - q)}^{2} \geq 0

, ahonnan

2 p^{2} + 2 q^{2} \geq p^{2} + 2 p q + q^{2} = {(p + q)}^{2} = 1

adódik. Innen

\begin{matrix} p^{m} \leq (2 p^{2} + 2 q^{2}) p^{m} = 2 p^{2} p^{m} + 2 q^{2} p^{m} \leq 2 p^{2} p^{m} + 2 q^{m} p^{2} = 2 p^{2} (p^{m} + q^{m}), \end{matrix}

ahol az utóbbi egyenlőtlenség

m \geq 2

és

q \geq p

miatt igaz. Nekünk pedig éppen ezt kellett bizonyítanunk.

□

Megjegyzés. Könnyen látható, hogy ha

p \leq \frac{1}{2}

, akkor

2 p^{2} \leq p

, és csakis akkor van egyenlőség, ha

p = \frac{1}{2}

vagy

p = 0

. Az

A

játékosnak tehát rosszabb az esélye a győzelemre, mint egyetlen labdamenet megnyerésére.
Az I. megoldásban található párbaállítási ötlet egyedül Paulin Roland dolgozatában fordult elő. A feladatot szintén megoldó további versenyzők mindegyike az ilyen feladatokra szokványosabb számolásos megoldással ért célt. Az alábbiakban erre mutatunk egy példát.

II. megoldás. Vegyük észre, hogy ha hat labdamenet után még nincs győztes, akkor mindkét játékos éppen három labdamenetet nyert. Világos, hogy annak a valószínűsége, hogy az

A

játékos

k

egymás utáni játszmából

l

-t nyer meg

(\binom{k}{l}) p^{l} q^{k - l}

, ahol

q : = 1 - p

B

játékos esélye egy labdamenet megnyerésére. Figyeljük meg, hogy ha a játék legfeljebb öt labdamenet után véget ér, akkor a végeredmény akkor sem változik meg, ha a játékosok végigjátsszák az első hat labdamenetet, hisz a vesztes még ekkor is csak legfeljebb két labdamenetet nyerhet. Az

A

játékos győzelmének valószínűsége tehát

\begin{matrix} P (A nyer) = p^{6} + 6 p^{5} q + 15 p^{4} q^{2} + 20 p^{3} q^{3} r, \end{matrix}

ahol az első tag a

6 : 0

-ás, a második az

5 : 1

-es, a harmadik a

4 : 2

-es győzelem valószínűsége,

r

pedig annak a valószínűsége, hogy

3 : 3

-as állás után az

A

játékos győz. A

3 : 3

-as állásnál vagy valamelyik játékos megnyeri a soron következő két labdamenetet és győz, vagy mindkét játékos egy-egy labdamenetet nyer, aminek a valószínűsége

2 p q

. Az így kialakult helyzetben azonban mindkét játékos győzelmi esélye azonos a

3 : 3

-as helyzetbeli esélyével. Tehát

r = p^{2} + 2 p q r

(hiszen

A

p^{2}

eséllyel nyeri meg a soron következő két labdamenetet), azaz

r = \frac{p^{2}}{1 - 2 p q}

. Azt kaptuk tehát, hogy

\begin{matrix} P (A nyer) = p^{6} + 6 p^{5} q + 15 p^{4} q^{2} + 20 p^{3} q^{3} \frac{p^{2}}{1 - 2 p q} . \end{matrix}

Nyilván

p q = p (1 - p) = \frac{1}{4} - {(p - \frac{1}{2})}^{2} \leq \frac{1}{4}

, ahonnan

\frac{1}{1 - 2 p q} \leq 2

adódik. Ezt felhasználva

\begin{matrix} P (A nyer) & \leq p^{6} + \frac{6}{4} p^{4} + \frac{15}{16} p^{2} + \frac{40}{64} p^{2} = p^{2} (p^{4} + \frac{3}{2} p^{2} + \frac{25}{16}) = \\ = p^{2} ({(p^{2} + \frac{3}{4})}^{2} + 1) \leq p^{2} ({(\frac{1}{4} + \frac{3}{4})}^{2} + 1) = 2 p^{2} . \end{matrix}

Egyenlőség pedig (

p \geq 0

miatt) pontosan akkor áll, ha

p^{2} = 0

vagy ha

p^{2} = \frac{1}{4}

, azaz, ha

p = 0

vagy

p = \frac{1}{2}

□

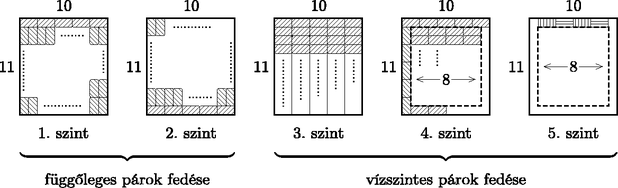
3. feladat.

2 \times 1

-es dominókból tornyot építünk a következő módon. Először elrendezünk

55

dominót úgy, hogy egy

10 \times 11

-es téglalapot fedjenek le; ez lesz a torony első szintje. Erre azután további,

55

dominót tartalmazó szinteket építünk, ügyelve arra, hogy minden egyes szint pontosan illeszkedjék az előzőre. Az így kapott építményt akkor nevezzük stabilnak, ha a

10 \times 11

-es téglalap minden rácsponttól különböző, belső pontja felett van dominónak belső pontja. Hány szintből áll a legalacsonyabb stabil torony?

Megoldás. Nevezzük a torony által lefedett téglalap

10

hosszú oldalát vízszintesnek, a

11

hosszút pedig függőlegesnek. A toronynak a feladatban leírt tulajdonsága azt jelenti, hogy az említett

10 \times 11

méretű téglalapot

(1 \times 1)

-es mezőkre osztva bármely két, élben szomszédos mezőhöz van a toronyban olyan dominó, amelyik pontosan e két mező felett található. A függőleges élek mentén szomszédos mezőpárokat nevezzük vízszintes pároknak ‐ 99 ilyen pár van ‐ a vízszintes élek mentén szomszédosakat pedig függőleges pároknak ‐ ezekből 100 darab van.
Először igazoljuk, hogy létezik

5

-szintes stabil torony. Világos, hogy két szint elegendő arra, hogy mind a 100 függőleges mezőpárt fedje dominó. A 99 vízszintes párnak a feladatban előírt ,,lefedéséhez'' három újabb szintet használunk fel. A téglalap vízszintes oldala páros, így kiparkettázható olyan dominókkal, amelyek kizárólag vízszintes párokat fednek le. Legyen ez a harmadik szint. Hagyjuk el a téglalap jobb és bal szélső oszlopát, valamint a legfelső sorát! A kapott

8 \times 10

-es tábla kiparkettázható csupa vízszintes dominóval. Ez a parkettázás kiterjeszthető az elhagyott szélső mezőkre is, legyen ez a negyedik szint. Mostanra a legfelső sor négy ,,belső'' párját kivéve minden vízszintes párról gondoskodtunk. Egy ötödik szinten ezek is lefedhetők, például az előzőhöz hasonló konstrukcióval, ha most a két szélső oszlopon kívül a legalsó sort hagyjuk el.

Állítjuk, hogy ha egy torony legfeljebb

4

-szintes, akkor nem stabil. Ebből következik, hogy a legalacsonyabb stabil torony éppen

5

-szintes. Indirekt módon bizonyítunk. Először is jegyezzük meg, hogy ha egy ilyen torony stabil, akkor legalább

4

szintje van. Valóban: a

10 \times 11

-es téglalap minden egyes, nem a szélen fekvő mezejének

4

szomszédja van, és az ezekhez tartozó dominók más-más szinten helyezkednek el. Ha tehát két szomszédos mező valamelyike nem szélső, akkor pontosan egy dominó fedi e két mezőt.
Ha egy

m

mezőnek

3

élszomszédja van (azaz

m

a téglalap szélén van, de nem sarokmező), akkor van egy olyan

m'

élszomszédja, hogy

m

és

m'

felett pontosan két dominó van a toronyban, ráadásul, az előbb elmondottak szerint

m'

szintén szélső mező. Az

m

mező további

2

élszomszédját pedig egy-egy

m

-et is fedő dominó fedi. Minthogy tetszőleges élszomszédos mezők között van olyan, amelynek

3

vagy

4

élszomszédja van, a fentiek szerint nincs olyan szomszédos mezőpár, amelyet a toronynak három dominója is fed.
Vizsgáljuk most már azokat a mezőpárokat, amelyeket a toronynak pontosan két dominója fed le! A fentiek szerint ezek a párok diszjunktak, a tábla szélén helyezkedhetnek el, továbbá az egyes sarokmezők mindkét szomszédjukkal ilyen kétszeresen fedett párt alkotnak. A bal alsó sarokmezőben végződő oszlop

11

mezején végighaladva azt találjuk, hogy vagy az oszlopban van olyan mező, amely nem szerepel kétszeresen fedett párban (ez lehetetlen), vagy az oszlop másik végében lévő sarokmező nincs duplán fedve az oszlopszomszédjával, amit szintén kizártunk. Ezzel a bizonyítást befejeztük, négyszintes stabil torony valóban nem létezik.

□