Cím: A 2005. évi WILLIAM LOWELL PUTNAM verseny feladatia
Füzet: 2006/január, 15 - 16. oldal  PDF  |  MathML 
Témakör(ök): Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A1. Bizonyítsuk be, hogy minden pozitív egész előáll egy vagy több 2r3s alakú szám összegeként (r és s nemnegatív egészek), úgy, hogy az összeg semelyik két tagja között sem áll fenn oszthatóság. (Például 23=9+8+6.)

 

 
A2. Legyen S={(a,b):a=1,2,...,n, b=1,2,3}. A p1,p2,...,p3n pontokat ebben a sorrendben összekötő töröttvonalat az S halmaz egy bástyabejárásának nevezzük, ha teljesülnek rá a következők: (i) p(i)∈S; (ii) pi és pi+1 egységnyi távolságra vannak minden 1≤i<3n esetén; (iii) minden p∈S esetén pontosan egy olyan i található, amelyre pi=p.
Hány olyan bástyabejárás van, amelyik az (1;1) pontban kezdődik és az (n;1) pontban ér véget?
(Az ábra egy lehetséges bástyabejárást mutat az n=5 esetb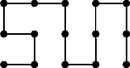en.)
 

 

A3. Tegyük fel, hogy az n-edfokú p(z) polinom valamennyi gyöke egységnyi abszolút értékű a komplex számsíkon. Legyen g(z)=p(z)zn/2. Bizonyítsuk be, hogy a g'(z)=0 egyenlet valamennyi gyöke egységnyi abszolút értékű.
 

A4. Legyen H olyan n×n-es mátrix, amelynek minden eleme 1 vagy -1 és a mátrix bármely két sora ortogonális. Bizonyítsuk be, hogy ha H-nak van olyan a×b méretű részmátrixa, amelynek minden eleme 1, akkor ab≤n.
 

A5. Határozzuk meg ∫01ln(x+1)x2+1dx értékét.
 

A6. Legyen az n≥4 adott egész szám. Tegyük fel, hogy a P1,P2,...,Pn pontokat egymástól függetlenül, véletlenszerűen, egyenletes eloszlás szerint választottuk egy körvonalon. Tekintsük azt az n oldalú konvex sokszöget, amelynek a Pi pontok a csúcsai. Mennyi a valószínűsége, hogy ennek a sokszögnek legalább az egyik belső szöge hegyeszög?
 

B1. Adjunk meg olyan nem zérus P(x,y) polinomot, amelyre minden valós a szám esetén teljesül, hogy P(⌊a⌋,⌊2a⌋)=0. (⌊t⌋ a t-nél nem nagyobb egész számok legnagyobbikát jelenti.)
 

B2. Határozzuk meg azokat az n,k1,...,kn pozitív egész számokat, amelyekre teljesül, hogy k1+k2+...+kn=5n-4, továbbá
1k1+...+1kn=1.
 

B3. Keressük meg mindazokat a differenciálható f:(0,∞)→(0,∞) függvényeket, amelyekhez létezik olyan a pozitív szám, hogy minden pozitív x számra
f'(ax)=xf(x).
 

B4. Adott pozitív egész m,n számokra jelölje f(m;n) azoknak az egész számokból álló (x1,x2,...,xn) n-eseknek a számát, amelyekre teljesül, hogy |x1|+|x2|+...+|xn|≤m. Bizonyítsuk be, hogy f(m;n)=f(n;m).
 

B5. Legyen a P(x1,...,xn) az x1,...,xn változók valós együtthatós polinomja. Tegyük fel, hogy
(a) (∂2∂x12+...+∂2∂xn2)P(x1,...,xn) azonosan nulla, továbbá hogy
(b) x12+...+xn2 osztja P(x1,...,xn)-et.

Bizonyítsuk be, hogy a P(x1,...,xn) polinom azonosan nulla.
 

B6. Jelölje Sn az 1,2,...,n számok permutációinak a halmazát. Ha π∈Sn, akkor legyen σ(π)=1, ha a π permutáció páros és legyen σ(π)=-1, ha a π permutáció páratlan. Jelölje ezen kívül ν(π) a π permutáció fixpontjainak a számát. Bizonyítsuk be, hogy
∑π∈Snσ(π)ν(π)+1=(-1)n+1nn+1.