Cím: Perfektség és normalitás
Szerző(k):  Patakfalvi Zsolt 
Füzet: 2006/január, 9 - 14. oldal  PDF  |  MathML 
Témakör(ök): Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A gráfelmélet a matematika egyik legközérthetőbb ága. Alapfogalmai többnyire a kívülállók számára is érthetők, akárcsak a problémák és azok háttere. Ezt kihasználva az alábbiakban gráfelméleti tudományos diákköri dolgozatom fő eredményét, illetve az ahhoz szorosan kapcsolódó fogalmakat ismertetem, semmilyen előismeretet nem feltételezve eközben az olvasótól.
Mint ahogy azt mindenki tudja, avagy talán már kitalálta, a gráfelmélet a gráfok vizsgálatával foglalkozik. A gráfok azt a helyzetet fogalmazzák meg a matematika nyelvén, amikor egy rendszer bizonyos elemei ,,kapcsolatban'' vannak egymással, mások pedig nem. A rendszer elemeiről beszélve gondolhatunk például emberekre, számítógépekre, városokra, a ,,kapcsolatok'' pedig jelenhetnek barátságot, számítógépek kábeleit, közvetlen repülőgépjáratokat, vagy bármi mást. Itt most csak olyan ,,kapcsolatokkal'' foglalkozunk, amelyek pontosan két elem közt állnak fenn; olyasmivel nem, mint például az ,,egy városban laknak'' kapcsolat, ami akár milliónyi ember közt is fennállhat. Azzal sem, hogy milyen ennek a kapcsolatnak a jellege, két ember nagyon szereti-e egymást vagy csak egy kicsit, illetve hogy két számítógépet egyetlen kábel köt-e össze vagy tizenhét; csak az a fontos, hogy megvan-e a kapcsolat vagy nincsen. Végül természetesen azzal sem törődünk, hogy maguk az elemek micsodák, milyen a belső szerkezetük, lehetnek molekulák, emberek, vagy hálózatban összekapcsolt szuperszámítógépek.
A fenti, némileg homályos leírás a megfelelő matematikai szóhasználattal precízzé tehető. Az ,,elemeket'' pontoknak vagy csúcsoknak, a ,,kapcsolatokat'' pedig éleknek nevezik. Két csúcsot él köt össze, vagy szomszédosak, ha az általuk ,,ábrázolt'' elemek kapcsolatban állnak egymással. Az így kapott objektumot hívjuk gráfnak. Még egyszer: egy gráf nem más, mint pontok és élek halmaza, azzal az információval kiegészítve, hogy melyik él melyik két pontot köti össze. Most csak ún. egyszerű gráfokkal foglalkozunk, azaz két pont közt nem lehet több él, és egy élnek nem lehet mindkét végpontja ugyanaz. Ha egy gráfot G-vel jelölünk, akkor V(G) és E(G) jelenti ezen gráf csúcsainak, illetve éleinek a halmazát.
Egy gráfot akár le is rajzolhatunk: a csúcsokat fekete pöttyökkel szoktuk jelölni, és ha két csúcs közt van él, akkor a nekik megfelelő két pöttyöt összekötjük egy folytonos vonallal, általában egy szakasszal. Az 1. ábrán lerajzoltunk néhány gráfot. Látható, hogy az élek a rajzon metszhetik egymást, a definíciókban ezt nem tiltottuk meg. Az ilyen metszéspontok valójában az ábrázolás miatt lépnek föl, a gráfnak általában nem csúcsai. Igazság szerint a gráf definíciójának semmi köze a rajzhoz, abban nincsenek se pöttyök, sem vonalak. Másféle ábrázolások is lehetségesek, gondoljunk arra, hogy egy számítógép memóriájában nem rajzolgathatunk, noha a gráfok számítógépes vizsgálata igen elterjedt módszer.

 
 

1. ábra
 

Ha két gráf kapcsolatoknak ugyanazt a rendszerét ábrázolja, azaz lényegileg ugyanazok, akkor azt mondjuk, hogy a két gráf izomorf. A megrajzolt ábrákról ez néha egyáltalán nem nyilvánvaló, szemléletesen mondjuk azt jelenti, hogy a lerajzolt diagramok egymásba mozgathatók úgy, hogy közben az éleik ne szakadjanak el. Precízen arról van szó, hogy a két gráf csúcsai között van egy olyan egy-egyértelmű megfeleltetés, ami szomszédos csúcspárokat szomszédosaknak, nem szomszédosokat pedig nem szomszédosaknak feleltet meg. Egy ilyen megfeleltetést a két gráf közti izomorfiának hívunk. Az 1. ábra a), b) és c) gráfjai például izomorfak, de a d) gráf nem izomorf egyikükkel sem, mert egyik csúcsának három szomszédja van, az első három gráfban viszont ilyen csúcs nem található.
Felmerülhet az olvasóban a kérdés, hogy miféle matematikai problémákat vethetnek fel ilyen egyszerű ábrák, amelyeket még a gyerekek is lerajzolhatnak. Nos, a gráfelmélet számára mind a külvilág, mind a matematika bőségesen kínál megoldandó problémákat. Az előbbire két klasszikus példa a königsbergi hidak, illetve a térképek színezésének feladata. Állítólag Eulertől kérdezték meg Königsberg lakói, bejárhatja-e valaki a városukat úgy, hogy a várost átszelő Pregel folyónak mind a hét hídján pontosan egyszer keljen át. A másik kérdést De Morgan egyik tanítványának a bátyja, egy bizonyos Francis Guthrie tette föl: azt szerette volna tudni, vajon minden térképen ki lehet-e színezni négy színnel az egyes országokat úgy, hogy a szomszédosak különböző színűek legyenek. Mindkét kérdés könnyen lefordítható a gráfok nyelvére. Az első esetben ez a fordítás lényegében kiadja a megoldást is. Ebben nincs semmi meglepő, a gráfok absztrakt nyelve magától értetődően tekint el a probléma szempontjából esetleges tulajdonságoktól, az ilyesmi pedig igen gyakran a döntő lépés egy-egy feladat megoldásakor. A második feladat, bár az elsőhöz hasonló fejtörőnek látszik, rendkívül nehéznek bizonyult, és eddig csak számítógép segítségével sikerült megoldani. Ezek a példák talán nem teljesen meggyőzőek, mert a környezetünkből származnak ugyan, de a megoldásnak látszólag nincs gyakorlati jelentősége. Egy séta akkor is kellemes lehet, ha nem jár be minden hidat, vagy egyeseket többször is érint, egy térképet pedig annyi színnel színezhetünk, amennyi tetszik. A kérdés messzire vezet és részben az elméleti és az alkalmazott matematika viszonyára vonatkozik. Anélkül, hogy a részletekbe bocsátkoznék, megemlítem, hogy az elvont matematikai ‐ és nem csak gráfelméleti ‐ kérdések vizsgálata során kifejlesztett fogalmak és módszerek igen gyakran bizonyulnak váratlanul hasznosnak olyan gyakorlati problémák megoldásában, amelyek a matematikai kérdés fölvetésekor semmilyen kapcsolatban nem voltak azzal, gyakran nem is léteztek. Ami pedig a gráfelméletet illeti, a mind nagyobb diszkrét rendszerek tömeges megjelenése az iparban, a gazdaságban, de gondolhatunk itt számítógéphálózatokra, vagy akár az internetre is, természetes módon teremti meg ennek a matematikai területnek a rendkívül fontos alkalmazásait.
A gyakorlatból jövő problémák mellett, illetve azokkal együtt számos gráfelméleti kérdés és fogalom forrása maga a matematika. Jó példa erre a Claude Berge által 1962-ben bevezetett perfekt gráfok fogalma. Berge egy gráfokhoz rendelt mennyiséget, egy ún. gráfparamétert, a Shannon-kapacitást tanulmányozta. A Shannon-kapacitás egy műszaki probléma, a hatékony kommunikáció elméleti vizsgálata során vetődött fel. Ha van egy kommunikációs csatorna, amely néha hibásan visz át információt, akkor ehhez a modellhez hozzárendelhetünk egy gráfot és ennek a gráfnak a Shannon-kapacitása adja meg a csatornán hiba nélkül elérhető maximális információátviteli sebességet. Vizsgálatai során Berge gráfoknak egy olyan osztályát találta meg, amelynek elemein rendkívül erős megszorítások érvényesek a Shannon-kapacitásra. Egészen pontosan az ilyen gráfokban két másik gráfparaméter, a klikkszám és a kromatikus szám értéke egyenlő és ezen gráfok Shannon-kapacitása éppen ez a közös érték.
A következőkben definiáljuk ezt a két gráfparamétert. A kromatikus szám az a legkisebb egész szám, ahány színnel egy gráf csúcsai kiszínezhetők úgy, hogy szomszédos csúcsok különböző színűek legyenek. (Ez a definíció emlékeztethet Guthrie térképszínezési feladatára.) Például az 1. ábra a), b) és c) gráfjának 3 a kromatikus száma, míg a d) gráfnak 2. A 2. ábrán ezeknek a gráfoknak ezt a minimális értéket megvalósító színezése látható. (Nyomdai okokból a színek helyett különböző jeleket használtam, remélem, a jelentésük világos.) Gondolja meg az Olvasó, hogy a közölt értékeknél kevesebb szín nem elég.
 
 

2. ábra
 

A klikkszám a legnagyobb klikk mérete a gráfban, ahol klikknek hívjuk a csúcsoknak olyan részhalmazát, amelynek bármely két eleme szomszédos. Az előző példákban nyilván valamennyi gráfnak 2 a klikkszáma, hiszen bármely két szomszédos csúcsuk egy klikket alkot, de három csúcsot tartalmazó klikk, úgynevezett teljes hármas vagy háromszög már nincs bennük.
A perfekt gráfok definiálásához még szükségünk van egy G gráf feszített részgráfjainak a fogalmára. Ezek egyszerűen azok a gráfok, melyeket úgy kapunk, hogy néhány csúcsot és az azokhoz csatlakozó összes élt kitöröljük G-ből. Fontos, hogy olyan éleket nem törlünk ki, amelyek két nem kitörölt csúcs közt mennek. Például a háromszög összes feszített részgráfja látható a 3. ábrán. Szaggatott vonal jelöli azokat a csúcsokat és éleket, amelyeket elhagyunk a háromszögből. Látható, hogy összesen nyolc feszített részgráfot kapunk. Egyikük maga a háromszög, három azzal a két csúcsú gráffal izomorf, amelyben a két csúcs szomszédos, másik három pedig az egypontú gráffal. Végül még nyilván megkapjuk az ún. üres gráfot, amelynek mind a csúcshalmaza, mind az élhalmaza az üres halmaz. Összefoglalva: a háromszögnek izomorfia erejéig négy feszített részgráfja van. Nyilván általában is 2n feszített részgráfja van egy n csúcsú gráfnak, amelyek közül az általános esetben sokan izomorfak egymással.
 
 

3. ábra
 

A fenti fogalmak birtokában már kimondhatjuk a perfekt gráfok definícióját. Egy gráf perfekt, ha minden feszített részgráfjának a klikkszáma megegyezik a kromatikus számával. Ez a definíció az olyan gráfokat írja le, amelyek kromatikus száma nem nagyobb a feltétlenül szükségesnél: egy gráf kromatikus száma ugyanis legalább akkora, mint a klikkszáma. Valóban, bármely klikk csúcsait különbözően kell színezni, lévén ezek a csúcsok szomszédosak. A perfekt gráfok azok, ahol ez a ,,természetes'' korlátozás az egyetlen megszorítás, bármely feszített részgráfjukat vesszük is szemügyre. A definíció alapján igen kellemetlen feladatnak látszik annak eldöntése, hogy egy adott gráf vajon perfekt-e. (Ez nem olyan ritka jelenség, gondoljunk arra, mivel járna, ha a definíció alapján kellene kiszámolnunk például sin20∘ vagy lg2 értékét.) Láttuk ugyanis, hogy egy gráfnak sok ‐ nagyon sok ‐ feszített részgráfja van, a klikkszám és a kromatikus szám meghatározása pedig már egyetlen nagyobb gráfra is nagyon nehéz lehet. Szerencsére, mint azt nemsokára látni fogjuk, a perfekt gráfokra bizonyított tételek jelentősen könnyítenek a helyzetünkön.
A perfekt gráfok a XX. század második felében központi szerepet játszottak a gráfelméleti kutatásokban. Ez köszönhető volt Berge két híres, nehéz, de azért megoldható sejtésének, a különféle kapcsolódási pontoknak az egyéb területekkel, illetve a rendkívül erős eredmények lelkesítő hatásának is. Berge első sejtése azt mondta ki, hogy egy gráf pontosan akkor perfekt, ha a komplementere is az. Egy G gráf komplementere az a gráf, melynek ugyancsak V(G) a csúcshalmaza, viszont két csúcs benne pontosan akkor van összekötve, ha G-ben nincs. Ezt a sejtést Lovász László bizonyította be 1972-ben, azóta Perfekt Gráf tételnek hívják az állítást. A bizonyítás megtalálható Lovász László: Kombinatorikai Problémák és Feladatok című könyvében.
A következő nagy eredmény ugyancsak Lovász László nevéhez fűződik. Egy német és egy holland matematikussal együtt sikerült belátnia, hogy van olyan algoritmus a perfekt gráfok kromatikus számának a meghatározására, amely a csúcsok számának egy rögzített polinomjánál kevesebb lépést megtéve megáll. Azt mondjuk ilyenkor, hogy a perfekt gráfok esetében van polinom idejű algoritmus a kromatikus szám meghatározására. Általában, nem perfekt gráfokra nem ismerünk ilyen algoritmust, sőt, él a sejtés, hogy nem is létezik.
Végül, de egyáltalán nem utolsósorban 2002-ben és 2003-ban jött a két nagyágyú, Berge második sejtésének, illetve ezt felhasználva a perfekt gráfok polinom idejű felismerhetőségének a bizonyítása. n-hosszú körnek hívjuk az n-oldalú sokszög által meghatározott gráfot, melynek pontjai a sokszög csúcsai, élei pedig az oldalai. Ezek alapján Berge második sejtése azt állítja, hogy egy gráf pontosan akkor perfekt, ha sem ő, sem pedig a komplementere nem tartalmaz feszített részgráfként öt vagy annál több pontból álló páratlan hosszú kört. Amióta a négy főből álló szerzőgárda (Chudnowsky, Robertson, Seymour és Thomas) publikálta a bizonyítást, ezt az állítást Erős Perfekt Gráf tételnek hívjuk. Míg a Perfekt Gráf tétel Lovász-féle bizonyítása lényegében két ‐ tömény ‐ tanítási óra alatt elmondható, ez a bizonyítás igen messze van ettől: körülbelül 150 oldalt tesz ki nyomtatásban.
Tudományos diákköri dolgozatomban a perfekt gráfok egy igen közeli rokonát, a normális gráfokat vizsgáltam. A normális gráfokat Körner János vezette be 1972-ben, mint a perfekt gráfok osztályának egy kiterjesztését. Ez egyrészt azt jelenti, hogy a normális gráfok definiálásakor bebizonyította, hogy minden perfekt gráf normális, másrészt mind ő, mind más kutatók azóta is sok hasonlóságot találtak a normális és a perfekt gráfok között. A normális gráfokra is teljesül például a Perfekt Gráf tétel megfelelője, azaz egy gráf pontosan akkor normális, ha a komplementere is az. A kutatásnak nagyjából az a filozófiája, hogy mivel a normális gráfok osztálya az eddigi eredmények alapján rendkívül hasonlít a perfekt gráfokéra, azt reméljük, hogy a perfekt gráfokra jellemző nagyon erős tulajdonságokból valamennyit sikerül normális gráfokra is bizonyítani.
A definícióval azonban még egy kicsit várnunk kell, mert előtte a független halmaz fogalmát kell tisztáznunk. Egy G gráf csúcsainak egy részhalmazát függetlennek hívjuk, ha az G komplementerében klikket alkot, azaz semelyik két pontja sem szomszédos G-ben. Ezt felhasználva, egy G gráf normális, ha létezik néhány független halmaza S1,S2,...,Sk, és néhány klikkje C1,C2,...,Cl úgy, hogy G-nek minden pontját tartalmazza valamely Si és valamely Cj, emellett bármely Si-nek és Cj-nek van közös pontja. Ebből a definícióból persze nem látszik, hogy miért is normális minden perfekt gráf, amire itt most nincs is lehetőségünk kitérni. Látszik viszont, amit korábban említettünk, hogy egy normális gráf komplementere normális, hiszen a komplementerben választhatjuk klikkeknek az eredeti gráf független halmazait és független halmazoknak az eredeti gráf klikkjeit. Az is könnyen bizonyítható közvetlenül a definícióból, hogy a páratlan hosszú körök közül csak az öt és a hét hosszúak nem normálisak. Ebből már az is látszik, hogy nem minden normális gráf perfekt, hiszen az Erős Perfekt Gráf tétel állításából tudjuk, hogy a legalább öt hosszú páratlan körök nem azok. Ehhez kapcsolódik az a Körner által megfogalmazott, sejtés is, amely ugyancsak a normális és perfekt gráfok közti kapcsolatot támasztaná alá, amennyiben igaznak bizonyulna. Ez a sejtés úgy szól, hogy egy gráfnak pontosan akkor normális minden feszített részgráfja, ha sem ő, sem a komplementere nem tartalmaz feszített részgráfként öt vagy hét hosszú kört. A normális gráfok bonyolult definíciójának megértésében segít a 4. ábra, ahol a kilenc hosszú kör normalitását mutatjuk meg vázlatosan. Az a) ábrán a definícióban megkövetelt klikkeket rajzoltuk be, míg a b), c) és d) ábrán a független halmazokat. Azt kell ellenőrizni, hogy minden pontot tartalmaz legalább egy klikk és legalább egy független halmaz, és hogy tetszőlegesen kiválasztva egy klikket és egy független halmazt, azok metszik egymást.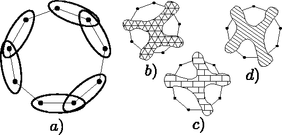
 
 

4. ábra
 

A perfekt gráfok irodalma hatalmas, úgyhogy rendkívül sok végtelen gráfcsaládot ismerünk, amelyek perfektek. Körner tétele alapján ezek mind normálisak is, úgyhogy ugyancsak sok normális gráfcsalád ismert. Olyan gráfcsaládok viszont, amelyek normálisak, de nem perfektek, ez idáig alig lettek azonosítva. Pontosabban a megfelelő páratlan körökön, illetve azok komplementerein kívül ilyen gráfosztály nem szerepel a szakirodalomban. Nem igazán tudjuk tehát, hogy mennyire különbözik a normális gráfok osztálya a perfektekétől. Dolgozatom fő állítása ezt a hiányt szándékozik betölteni. Azt bizonyítom be, hogy minden 3-reguláris gráf élgráfja normális. Egy gráf 3-reguláris, ha minden csúcsának három szomszédja van, egy G gráf élgráfja pedig az a gráf, melynek pontjai G éleinek felelnek meg, és két pont pontosan akkor szomszédos, ha G-ben a nekik megfeleltetett élek ugyanazon ponthoz csatlakoznak. Az nyilvánvaló, hogy a 3-reguláris gráfok élgráfjai közt végtelen sok nem perfekt van, és az is könnyen látszik, hogy ezek a gráfok normálisak, amennyiben az eredeti 3-reguláris gráf élei kiszínezhetők három színnel úgy, hogy az egymáshoz csatlakozók különböző színűek legyenek. Ráadásul ismeretes, hogy 3-reguláris gráfok élei három vagy négy színnel színezhetők ilyen módon. Azon gráfokra viszont, amelyekre az eredeti 3-reguláris gráf élei csak négy színnel színezhetők, az állítás egyáltalán nem nyilvánvaló. Ebbe a jelenségbe más gráfelméleti tételeknél és sejtéseknél is beleütközünk: az adott probléma lényegi esetei a 3-reguláris, három színnel nem élszínezhető gráfok. Ilyen például a már korábban emlegetett térképek négy színnel színezhetőségének a problémája. Az állításom bizonyításáról itt, most nincs lehetőség bővebben írni. Annyit mondanék róla, hogy a matematikában szokásos módon egy másik jól ismert problémára vezeti vissza a kérdést: az én esetemben ez a párosítások keresése páros gráfokban.