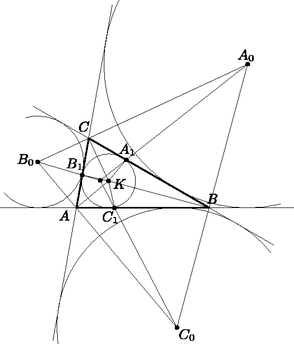Kezdőlap


Cím:	A Ceva-tétel trigonometrikus alakja és néhány alkalmazása
Szerző(k):	Kiss Márton
Füzet:	2005/december, 514 - 518. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Giovanni Ceva (1647‐1736) olasz matematikus tétele arra ad szükséges és elégséges feltételt, hogy egy háromszög egy-egy csúcsán áthaladó három egyenes mikor párhuzamos, vagy metszi egymást egy pontban. Bevezetésképpen idézzük fel a tételt:

1. tétel (Ceva tétele). Legyen

D

E

F

rendre az

A B C

háromszög

B C

A C

és

A B

oldalának egy-egy pontja.

\frac{A F}{F B} \cdot \frac{B D}{D C} \cdot \frac{C E}{E A} = 1

akkor és csak akkor, ha az

A D

B E

és

C F

egyenesek egy ponton mennek át, vagy párhuzamosak.

A bizonyítás megtalálható például Hajós György: Bevezetés a geometriába c. könyvében [2].
Sok feladatban azonban az említett feltétel bonyolult számításokra vezet. Versenyeken, ahol a feladatok megoldása időhöz van kötve, fontos, hogy minél egyszerűbb, könnyebben használható feltételeket tudjunk felírni. A Ceva-tétel következő, trigonometrikus alakját Matolcsi Máté dolgozatából [4] vettem át:

2. tétel (Ceva tétele, trigonometrikus változat). Az

A D

B E

és

C F

egyenesek akkor és csak akkor párhuzamosak vagy mennek át egy ponton, ha

\begin{matrix} \frac{sin B A D ∢}{sin D A C ∢} \cdot \frac{sin C B E ∢}{sin E B A ∢} \cdot \frac{sin A C F ∢}{sin F C B ∢} = 1, \end{matrix}

azaz az

A D

B E

és

C F

szakaszok megfelelő oldalaktól vett távolságarányainak szorzata

1

(1. ábra).

1. ábra

Bizonyítás. Bocsássunk merőlegeseket

D

-ből az

A B

és

A C

oldalakra! A talppontok legyenek

A_{1}

és

A_{2}

. Tegyük fel, hogy

A D

B E

és

C F

egy ponton mennek át. Vegyük észre, hogy

\begin{matrix} \frac{sin B A D ∢}{sin D A C ∢} = \frac{D A_{1}}{D A_{2}} = \frac{B D sin β}{D C sin γ} \end{matrix}

és ez éppen az

A D

egyenesnek az

A B

és

A C

oldalegyenesektől mért távolságaránya. Hasonlóképpen

\frac{sin C B E ∢}{sin E B A ∢} = \frac{C E sin γ}{E A sin α}

, valamint

\frac{sin A C F ∢}{sin F C B ∢} = \frac{A F sin α}{F B sin β}

. Összeszorozva

\begin{matrix} \frac{sin B A D ∢}{sin D A C ∢} \cdot \frac{sin C B E ∢}{sin E B A ∢} \cdot \frac{sin A C F ∢}{sin F C B ∢} & = \frac{B D sin β}{D C sin γ} \cdot \frac{C E sin γ}{E A sin α} \cdot \frac{A F sin α}{F B sin β} = \\ = \frac{B D}{D C} \cdot \frac{C E}{E A} \cdot \frac{A F}{F B} = 1. \end{matrix}

Megfordítva, ha

\begin{matrix} \frac{sin B A D ∢}{sin D A C ∢} \cdot \frac{sin C B E ∢}{sin E B A ∢} \cdot \frac{sin A C F ∢}{sin F C B ∢} = 1, \end{matrix}

akkor ugyanígy bizonyíthatjuk, hogy

\frac{B D}{D C} \cdot \frac{C E}{E A} \cdot \frac{A F}{F B} = 1

, azaz

A D

B E

és

C F

egy ponton mennek át.

□

Egy szintén rövid, ám Ceva tételét nem használó bizonyítás olvasható a KöMaL egy régebbi számában [1]. Megjegyzendő, hogy a tétel mindkét változata szerepel a Theorems in the geometry of the triangle c. angol nyelvű jegyzetben [3].
Térjünk most már rá az alkalmazásokra. Figyeljük meg, hogy az alábbiakban az eredeti Ceva-tételt csak nehézkesen tudnánk alkalmazni, míg a trigonometrikus változat a szinusz-tétel segítségével jól alakítható összefüggéseket eredményez.

1. feladat. Legyenek a hegyesszögű

A B C

háromszög oldalaira írt hasonló egyenlőszárú háromszögek

A B C_{1}

B C A_{1}

és

C A B_{1}

. Ekkor az

A A_{1}

B B_{1}

és

C C_{1}

szakaszok egy ponton mennek át (2. ábra).

2. ábra

Bizonyítás. A módosított Ceva-tételt alkalmazzuk:

\begin{matrix} \frac{sin B A A_{1} ∢}{sin A_{1} A C ∢} \cdot \frac{sin C B B_{1} ∢}{sin B_{1} B A ∢} \cdot \frac{sin A C C_{1} ∢}{sin C_{1} C B ∢} = \\ = & \frac{A_{1} C}{sin A_{1} A C ∢} \cdot \frac{sin B A A_{1} ∢}{B A_{1}} \cdot \frac{B_{1} A}{sin B_{1} B A ∢} \cdot \frac{sin C B B_{1} ∢}{C B_{1}} \cdot \frac{C_{1} B}{sin C_{1} C B ∢} \cdot \frac{sin A C C_{1} ∢}{A C_{1}} = \\ = & \frac{A_{1} A}{sin A_{1} C A ∢} \cdot \frac{sin A B A_{1} ∢}{A_{1} A} \cdot \frac{B_{1} B}{sin B_{1} A B ∢} \cdot \frac{sin B C B_{1} ∢}{B_{1} B} \cdot \frac{C_{1} C}{sin C_{1} B C ∢} \cdot \frac{sin C A C_{1} ∢}{C_{1} C} = \\ = & \frac{sin A B A_{1} ∢}{sin A_{1} C A ∢} \cdot \frac{sin B C B_{1} ∢}{sin B_{1} A B ∢} \cdot \frac{sin C A C_{1} ∢}{sin C_{1} B C ∢} = 1, \end{matrix}

ahol az első lépésben azt használtuk ki, hogy a háromszögek egyenlő szárúak, a második lépésben pedig a szinusz-tételt. Végül a számlálóban és a nevezőben egyenlő szögek maradtak, hiszen az oldalakra írt háromszögek hasonlósága miatt

A B A_{1} ∢ = C_{1} B C ∢

B C B_{1} ∢ = A_{1} C A ∢

és

C A C_{1} ∢ = B_{1} A B ∢

□

A következő feladat az 1990. évi Kürschák-versenyen szerepelt:

2. feladat (Kürschák-feladat). Az

A B C

háromszög beírt körének középpontja legyen

K

, a hozzáírt körök középpontjai legyenek

A_{0}

B_{0}

C_{0}

. Jelölje

A_{1}

B C

oldal és a

B K C

szög felezőjének,

B_{1}

A C

oldal és a

A K C

szög felezőjének,

C_{1}

pedig az

A B

oldal és a

A K B

szög felezőjének a metszéspontját. Ekkor az

A_{0} A_{1}

B_{0} B_{1}

C_{0} C_{1}

egyenesek egy ponton mennek át.

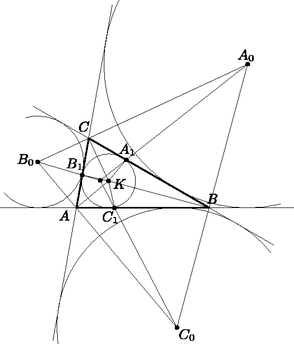3. ábra

Bizonyítás.

A_{0}

B_{0}

C_{0}

a megfelelő külső szögfelezők metszéspontja, így az

A

B

C

csúcsok az

A_{0} B_{0} C_{0}

háromszög oldalaira esnek. Az

A_{0} A_{1}

egyenesre vonatkozó távolságarány az

A_{0} B_{0} C_{0}

háromszögben

\begin{matrix} \frac{C A_{1} \cdot sin B C A_{0} ∢}{A_{1} B \cdot sin C B A_{0} ∢} = \frac{C A_{1} \cdot cos \frac{γ}{2}}{A_{1} B \cdot cos \frac{β}{2}} . \end{matrix}

Hasonlóan kaphatók a

B_{0} B_{1}

és a

C_{0} C_{1}

egyenesre vonatkozó távolságarányok, így e három arány szorzata

\begin{matrix} \frac{C A_{1}}{A_{1} B} \cdot \frac{A B_{1}}{B_{1} C} \cdot \frac{B C_{1}}{C_{1} A} . \end{matrix}

A szögfelezőtétel szerint másfelől

\begin{matrix} \frac{C A_{1}}{A_{1} B} = \frac{C K}{B K}, \frac{A B_{1}}{B_{1} C} = \frac{A K}{C K} és \frac{B C_{1}}{C_{1} A} = \frac{B K}{A K}, \end{matrix}

az említett három arány szorzata tehát

1

. Ceva tételének módosított változata szerint tehát az

A_{0} A_{1}

B_{0} B_{1}

C_{0} C_{1}

egyenesek egy ponton mennek át.

□

A következő feladat egy olimpiai válogatóversenyen szerepelt 1991-ben:

3. feladat. Legyenek a

P Q R S T U

hatszög szemközti oldalai párhuzamosak. Igazoljuk, hogy a szemközti oldalak felezőpontjait összekötő

M_{P Q} M_{S T}

M_{Q R} M_{T U}

és

M_{R S} M_{U P}

szakaszok egy ponton mennek át (4. ábra).

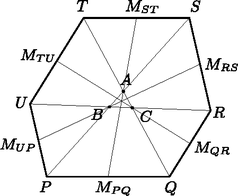4. ábra

Bizonyítás. Hogy a Ceva-tételt alkalmazhassuk, találnunk kell egy olyan háromszöget, amelynek a csúcsain mennek át a megadott szakaszok. Húzzuk meg a

P S

Q T

és

R U

átlókat. Ismeretes, hogy egy trapéz átlóinak a metszéspontja rajta van a trapéz párhuzamos oldalait összekötő középvonalán, ezért például

M_{P Q}

A

és

M_{S T}

egy egyenesen vannak. (Valóban,

P Q

és

S T

párhuzamossága miatt az

A P Q

és az

A S T

háromszögek hasonlóak. Az

A

fixpontú középpontos hasonlóság, ami

P

-t

S

-be,

Q

-t pedig

T

-be viszi át,

M_{P Q}

-t

M_{S T}

-be viszi, tehát ezek egyenese áthalad

A

-n.) Egy kis átfogalmazással most már az a feladatunk, hogy belássuk, hogy az

A B C

háromszög csúcsain áthaladó

M_{P Q} M_{S T}

M_{Q R} M_{T U}

és

M_{R S} M_{U P}

egyenesek egy ponton mennek át. Írjuk fel

M_{P Q}

távolságát az oldalaktól. Most azonban ne az

A

csúcsnál levő szöge(ke)t használjuk, hanem az

A P Q

háromszög másik két szögét, amelyekről többet tudunk. Eszerint

M_{P Q}

távolsága az

A B

és

A C

oldalaktól

P M_{P Q} \cdot sin S P Q ∢

, illetve

M_{P Q} Q \cdot sin P Q T ∢

, és minthogy

M_{P Q}

felezőpont, ezek aránya

\frac{sin S P Q ∢}{sin P Q T ∢}

. A szinusz-tétel szerint ez megegyezik

\frac{A Q}{A P}

-vel, ami az

A P Q

és az

A T S

háromszögek már említett hasonlósága miatt

\frac{Q T}{P S}

-sel egyenlő. Hasonlóan kapjuk, hogy

M_{R S}

-nek a

B C

és

B A

oldalegyenesektől vett távolságainak aránya

\frac{P S}{U R}

, míg

M_{T U}

távolságainak aránya a

C A

és

C B

oldalegyenesektől

\frac{U R}{Q T}

. Ezen arányok szorzata

1

, tehát

M_{P Q} M_{S T}

M_{Q R} M_{T U}

és

M_{R S} M_{U P}

valóban egy ponton mennek át.

□

Végül egy érdekes típusfeladat:

4. feladat. Legyenek az

A B C

háromszögben az

A D

B E

és

C F

szögfelezők, a

D E F

háromszögben pedig a

D G

E H

és

F I

szakaszok magasságok. Bizonyítsuk be, hogy ekkor az

A G

B H

és

C I

szakaszok egy ponton mennek át.

Ha pusztán az eredeti Ceva tétellel bizonyítanánk, meglehetősen sok, bonyolult arányt kellene kiszámítanunk. Szerencsére az általunk használt trigonometrikus változattal egy egyszerű, egyben jóval általánosabb állítást kapunk.

5. feladat. Ha az

A B C

háromszögben az

A D

B E

és

C F

szakaszok egy ponton mennek át, valamint a

D E F

háromszögben a

D G

E H

és

F I

szakaszok egy ponton mennek át, akkor az

A G

B H

és

C I

szakaszok is egy ponton mennek át.

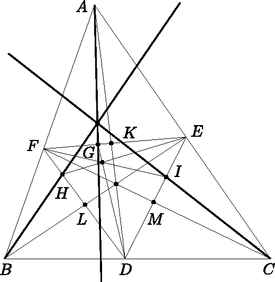5. ábra

Bizonyítás. Legyen

K

A D

és

E F

L

B E

és

D F

M

pedig a

C F

és

D E

szakaszok metszéspontja.

K

távolsága

A B

-től és

A C

-től

F K \cdot sin A F K ∢

, illetve

K E \cdot sin K E A ∢

. Hasonlóan írhatjuk fel

L

és

M

távolságát az

A B C

háromszög megfelelő oldalaitól. Mivel

A K

B L

és

C M

egy ponton mennek át, felírhatjuk a Ceva-tétel módosított változatát az

A B C

háromszögben:

\begin{matrix} \frac{F K \cdot sin A F K ∢}{K E \cdot sin K E A ∢} \cdot \frac{D L \cdot sin B D L ∢}{L F \cdot sin L F B ∢} \cdot \frac{E M \cdot sin C E M ∢}{M D \cdot sin M D C ∢} = 1. \end{matrix}

(1)

Másrészt a

D E F

háromszögre felírva az eredeti Ceva-tételt:

\begin{matrix} \frac{E K}{K F} \cdot \frac{F L}{L D} \cdot \frac{D M}{M E} = 1. \end{matrix}

(2)

Megszorozva ezzel az előző egyenletet, azt kapjuk, hogy

\begin{matrix} \frac{sin A F K ∢}{sin K E A ∢} \cdot \frac{sin B D L ∢}{sin L F B ∢} \cdot \frac{sin C E M ∢}{sin M D C ∢} = 1. \end{matrix}

(3)

Hátra van még, hogy azt is kihasználjuk, amit a

D G

E H

és

F I

szakaszokról tudunk. A

D E F

háromszögben alkalmazva Ceva tételét,

\begin{matrix} \frac{E G}{G F} \cdot \frac{F H}{H D} \cdot \frac{D I}{I E} = 1. \end{matrix}

(4)

Elosztva ezzel (3)-at:

\begin{matrix} \frac{F G \cdot sin A F K ∢}{G E \cdot sin K E A ∢} \cdot \frac{D H \cdot sin B D L ∢}{H F \cdot sin L F B ∢} \cdot \frac{E I \cdot sin C E M ∢}{I D \cdot sin M D C ∢} = 1, \end{matrix}

(5)

ez az egyenlőség pedig éppen azt állítja, hogy az

A G

B H

és

C I

szakaszok megfelelő oldalaktól vett távolságarányainak szorzata

1

, azaz Ceva tételének módosított változata szerint ezek a szakaszok is egy ponton mennek át.

□

Köszönetet szeretnék mondani Matolcsi Máténak a cikk alapötletéért, és azért is, hogy [4] dolgozatát felhasználhattam.

Hivatkozások

[1]	Surányi János: Az 1990. évi Kürschák József Matematika Tanulóverseny feladatainak megoldása, Középiskolai Matematikai Lapok, 41 (1991), 51‐61.

[2]	Hajós György: Bevezetés a geometriába, Tankönyvkiadó (Budapest, 1972).

[3]	P. Körtesi: Theorems in the geometry of the triangle, Junior Mathematical Society Miskolc (Miskolc, 1998).

[4]	M. Matolcsi: Ceva's theorem and a few extensions, Extended Essay (Atlantic College, 1993).