Kezdőlap


Cím:	Beszámoló a 2005. évi Nemzetközi Informatikai Diákolimpiáról
Szerző(k):	Horváth Gyula , Zsakó László
Füzet:	2005/november, 485 - 487. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 2005. augusztus 18‐25 között rendezték a 2005. évi Nemzetközi Informatikai Diákolimpiát (IOI) Lengyelországban, Nowy Sa̧cz-ban. A versenyen 77 ország 276 versenyzője vett részt.
Versenyzőink közül Kormányos Balázs ezüstérmet, Stippinger Marcell, Tassy Gergely és Ludányi Ákos bronzérmet szerzett. A verseny az elmúlt évekhez képest szakmailag is korrekt volt, bár a feladatok egysíkúak voltak és elsősorban matematikai tudást igényeltek.
A magyar résztvevők és eredményeik:

\begin{matrix} 62. & Kormányos Balázs & Szeged, Radnóti Miklós Gimnázium, 11. osztály \\ 73. & Stippinger Marcell & Sopron, Széchenyi István Gimnázium, 12. osztály \\ 98. & Tassy Gergely & Budapest, Veres Péter Gimnázium, 12. osztály \\ 120. & Ludányi Ákos & Eger, Neumann János Középiskola, 11. osztály \end{matrix}

Eredményünk a tavalyihoz képest tovább javult, 2000 után először újra mindegyik versenyzőnk érmet szerzett, s ezzel az országok sorrendjében is előre léptünk. Kiemelkedően szerepelt Kína, az Egyesült Államok és Szlovákia csapata. Új jelenség a diákolimpián újabb távol-keleti országok (Tajvan, Thaiföld, Hongkong, Indonézia, illetve India) határozott előretörése.
Sok sikeresebben szereplő ország példája azt mutatja, hogy az eredményes szerepléshez korszerű tehetséggondozó rendszerre van szükség. Ennek alapja ma is létezik, a Nemes Tihamér OKSZTV és az Informatika OKTV. Erre épül a két éve indított Neumann János Tehetséggondozó Program, amely regionális szinten terveink szerint idén is 400, országos szinten pedig 60 tehetséges diákot készített fel, havi 1‐1 foglalkozáson. A nemzetközi tapasztalatok alapján erre épül egy Internetes tehetséggondozó program a legjobb 12‐15 tanulónak, akik nagy eséllyel pályázhatnak az olimpiai csapatba kerülésre.
A 20‐25 fős diákolimpiai válogatóversenyt is egy felkészítéshez kapcsoljuk, amelyen a tavalyihoz hasonlóan 6 versenyzőt választunk ki. A verseny után következik az olimpikonok felkészítése, újabb versennyel, ahol kiválasztjuk a végleges, 4 fős olimpiai csapatot. Ezután következhet az intenzív felkészülés, amelyre így további 1‐2 hónap áll rendelkezésre.
Ízelítőül egy feladat az olimpia 6 feladatából:

Byteman születésnapján

n

gyerek vesz részt,

1

-től

n

-ig sorszámozzuk őket. Egy kerek asztal köré

n

székre ültek sorszámuk alapján az óramutató járása szerinti sorrendben.
Byteman szülei tudják, hogy a gyerekek nagy zajt csapnak, ha nem megfelelő az ültetési sorrend. Egy ültetési sorrend a

p_{1}, p_{2}, ..., p_{n}

permutációval írható le (

p_{1}, p_{2}, ..., p_{n}

különböző egészek

1

és

n

között). Ez azt jelenti, hogy

p_{1}

p_{n}

és

p_{2}

között ül, a

p_{i}

(i = 2,3, ..., n - 1)

p_{i - 1}

és a

p_{i + 1}

között, a

p_{n}

pedig a

p_{n - 1}

és a

p_{1}

között.
Mivel a gyerekek már leültek sorszám szerinti sorrendben, ezért újra kell őket ültetni a megfelelő ültetési sorrendbe úgy, hogy egyszerre felállnak és mindenki a korábbi helyétől valahány hellyel balra vagy jobbra lépve ül le, hogy a kívánt elhelyezés kialakuljon.
Az átültetés zaja arányos a legmesszebbre lépő gyerek lépésszámával. A gyerekek többféleképpen is átültethetők. A cél a lehető legcsendesebb átültetés.
Feladat: Készíts programot, amely kiszámítja a lehető legkisebb távolságot, amit a legmesszebbre lépő gyereknek meg kell tennie!
Bemenet: A standard bemenet első sorában a gyerekek

n

száma van (

1 \leq n \leq 1 000 000

). A második sor a gyerekek megfelelő ültetési sorrendjét megadó

n

egész számot tartalmazza:

p_{1}, p_{2}, ..., p_{n}

egy-egy szóközzel elválasztva.
Kimenet: A standard kimenet egyetlen sorába a megfelelő sorrend eléréséhez szükséges lehető legkisebb távolságot kell írni, amit a legmesszebbre lépő gyereknek meg kell tennie!
Példa: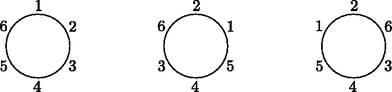

\begin{matrix} Bemenet: & Helyes kimenet: \\ 6 & 2 \\ 3 4 5 1 2 6 \end{matrix}

A baloldali ábrán a kezdeti sorrend látható. A középső ábrán egy lehetséges ültetési sorrend van: az 1-es és a 2-es gyerek egyet lép, a 3-as és az 5-ös kettőt, a 4-es és a 6-os helyben marad. A jobboldali ábra egy másik lehetséges optimális átültetést mutat, ellentétes irányban.