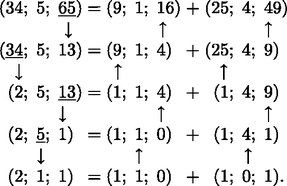|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A tavalyi pontverseny utolsó feladatai között a májusi számunkban tűztük ki a B. 3822. és az A. 376. feladatokat. Mindkettő egy számhármasokon definiált különös eljárásra vonatkozott. Ebben a cikkben a feladatok hátterét szeretném bemutatni. Remélem, kiderül, hogy a feladatokban megadott eljárás nagyon is eleven kapcsolatban van a számelmélet egy gazdag fejezetével, a másodfokú diofantikus egyenletek elméletével.
B. 3822. Az számhármassal egy lépésben a következőt lehet tenni: tetszőlegesen felcserélhetjük a számokat, vagy lecserélhetjük az számhármasra. El lehet-e jutni ilyen lépésekkel a számhármasból az számhármasba?
A továbbiakban az jelölést használjuk arra, hogy a fenti lépésekkel az számhármasból el lehet jutni az számhármasba. Természetesen , továbbá ha és , akkor . Vegyük észre, hogy | |
a számok felcserélését és ezen második műveletet is el lehet végezni ,,visszafelé''. Így ha , akkor . A ekvivalenciareláció; ekvivalenciaosztályokra bontja a számhármasokat, a feladat pedig azt kérdezi, hogy az és a számhármasok azonos ekvivalenciaosztályokban vannak-e. Az A. 376. feladat ugyanezt a kérdést teszi fel az és számhármasokról.
Néhány észrevétel
A továbbiakban invariánsokat keresünk: olyan jellemzőket, amelyek egy lépés során nem változnak meg. Ha egy ilyen invariáns ,,értéke'' két számhármasra különböző, akkor az egyikből nem lehet eljutni a másikba, különböző ekvivalenciaosztályban vannak. Triviális példa a számhármasok tagjainak egész volta: egy lépés során egészekből álló számhármasból csak egészekből álló számhármast kaphatunk, így például az -ból nem juthatunk el az vagy az számhármasba. Ez az invariáns azonban egyik feladatot sem oldja meg, túl gyenge. Ígéretesebbnek tűnhet a számhármas elemeinek a legnagyobb közös osztója. (Gondoljuk meg, hogy ‐ ha eltekintünk az előjelektől ‐ akkor ez valóban invariáns.) A kitűzött feladatokban sajnos ez a legnagyobb közös osztó minden esetben 1, tehát ez az invariáns sem segít. Annyit azért érdemes megjegyeznünk, hogy mivel az adott lépések, illetve a számhármasok tagjainak egy adott egésszel való szorzása felcserélhető, akkor és csak akkor teljesül, ha . Így ‐ ha kényelmes ‐ föltehető, hogy számhármasaink legnagyobb közös osztójaÍ1. Most viszont mutatunk egy ravaszabb invariánst.
I. megoldás a B. 3822. feladatra. Tekintsük az , , számokat és legyen az ezen számok közül a hárommal oszthatók száma. Ha felcseréljük a számokat, akkor értéke természetesen nem változik. Megmutatjuk, hogy a második művelet esetén sem változik!
az , , számok közül a 3-mal oszthatók száma, de pontosan akkor, ha , hiszen Tehát értéke nem változik a lépések során, ugyanakkor , míg , hiszen az első esetben csak teljesül, míg a második esetben és .
A két számhármas tehát különböző ekvivalenciaosztályban van, így a számhármasból nem lehet eljutni az számhármasba.
Ez az invariáns sajnos nem oldja meg az A. 376. feladatot: . Mivel , az sem derül ki, hogy vagy teljesül-e. A következő invariáns segítségével viszont sikerül majd ,,szétválasztanunk'' a B. feladat számhármasait az A. feladat számhármasaitól.
II. megoldás a B. 3822. feladatra. Tekintsük a következő kifejezést: | |
Az első alakból látszik, hogy invariáns a számok felcserélésére; a másodikból pedig az, hogy a második műveletre is. Mivel és , azért a számhármasból nem juthatunk el az számhármasba. Üröm az örömben, hogy az A. 376. feladatot még mindig nem sikerült megoldanunk: . Annyi mindenesetre kiderült, hogy a B. feladat számhármasaiból az A. feladat egyik számhármasába sem lehet eljutni.
A számhármasok normája
Alakítsuk át a fenti kifejezést!
Tehát pontosan akkor, ha . Ebben az esetben | |
Ez azt jelenti, hogy ha , akkor négyzetszám. Így például ha , akkor négyzetszám (és a szimmetria miatt persze és is négyzetszámok). Hasonlóan, ha , akkor (valamint és ) négyzetszám.
Ha , akkor hívjuk az mennyiséget az számhármas normájának. Vegyük észre, hogy invariáns, egy ‐ páros összegű számhármasokból álló ‐ ekvivalenciaosztályon belül tehát nyugodtan beszélhetünk -ről. Ha például igaz volna a megfordítás, tehát hogy egyenlő normájú számhármasok ekvivalensek is, akkor ebből igenlő válasz következne az A. 376. feladatra. A továbbiakban -vel számolunk majd, de eredményeinket -re fogalmazzuk meg: így elegánsabb formába írhatók.
Szükségünk lesz arra, hogy -t kifejezzük , , segítségével. Nyilván A korábbiak szerint a fenti kifejezésben négyzetszám áll a gyökjel alatt. Mint látható, egy számhármas két tagja a normával együtt sem határozza meg egyértelműen a harmadik elemet: két lehetőség adódik.
A következő önmagában is érdekes lemma olyan számhármasokról szól, amelyek normája nulla. Ilyen persze a , amivel nem sokra megyünk, a legegyszerűbb nem triviális példa a .
1. lemma. -ből csak alakú számhármasokba juthatunk el.
Bizonyítás. Látszólag kitüntetett szerepe van a harmadik koordinátának, valójában , így azt is írhatjuk, hogy -ből csak az alakú számhármasokba lehet eljutni, ahol . Az nyilvánvaló, hogy két elem cseréje nem változtatja meg az alak jellegét, nincs kitüntetett szerepe a harmadik koordinátának.
Mivel , így a második lépést végrehajtva az számhármast kapjuk, ami láthatóan a kívánt alakú. Mivel a kezdeti is ilyen, azért minden lépés után az alakú számhármasok körében maradunk.
A látottak szerint nyugodtan végrehajthatjuk az és az lépéseket is, hiszen ezek összerakhatók két cseréből és egy második fajta műveletből. A harmadik koordinátának tehát nincsen semmilyen kitüntetett szerepe.
Vegyük észre azt is, hogy transzformációink lineárisak, azaz ha akkor | |
ahol koordinátánként adunk össze. Ugyanígy végezhetjük ,,tagonként'' a koordináták felcserélését is, ügyelve arra, hogy ugyanazokat a cseréket hajtsuk végre a felbontásban szereplő számhármasokban.
Aratás
Tegyünk egy kitérőt és nézzük meg, hogy klasszikus számelméleti eredmények hogyan fogalmazhatók meg ebben a megközelítésben. Egy híres probléma, a két négyzet összegeként felírható számok jellemzésének kulcsa az alábbi
1. tétel. alakú szám minden pozitív osztója felírható két négyzetszám összegeként.
Bizonyítás. Ha , akkor van olyan pozitív egész, hogy . A döntő észrevétel az, hogy mostani jelöléseinkkel ez az egyenlőség azt jelenti, hogy Vizsgáljuk meg tehát az feltételt kielégítő számhármasokat! Az alábbi lemma azt mondja ki, hogy a értékű norma lényegében egyetlen ekvivalenciaosztályt azonosít.
2. lemma. Ha és , akkor , tehát ezek a számhármasok az ekvivalenciaosztályát alkotják.
Ilyen például a B. feladat számhármasa és valóban: ha mindig a legnagyobb számot cseréljük ki, akkor két lépésben: .
A 2. lemma bizonyítása. Ha , akkor , vagyis , , egyszerre pozitív vagy negatív. A feltétel szerint , így mindhárom szám pozitív. Megmutatjuk, hogy . Azt állítjuk, hogy ha a példához hasonlóan minden lépésben a legnagyobb számot cseréljük ki, akkor értéke nem nő és csak akkor nem csökken, ha az egy permutációjával van dolgunk. Mivel számaink pozitívak, az összegük is az; ha pedig ez az összeg lépésenként csökken, előbb-utóbb valóban el kell jutnunk az számhármashoz.
Az általánosság megszorítása nélkül föltehető, hogy . A fentiek szerint ekkor -t cseréljük ki -re és azt kell bizonyítanunk, hogy , vagyis .
Ha , azaz , akkor , készen vagyunk. Megmutatjuk, hogy ha (és ), akkor a -re adódó két érték kisebbike, . Így csak lehetséges, tehát , amit bizonyítani akartunk.
Állításunk ekvivalens az , azaz a négyzetre emeléssel kapott egyenlőtlenséggel. Feltevésünk szerint , továbbá miatt . Innen pedig már leolvasható a bizonyítandó egyenlőtlenség.
Ezzel bebizonyítottuk, hogy , esetén . A bizonyításból az is látszik, hogy ha és , akkor .
Térjünk most vissza az 1. tétel bizonyításához. Láttuk, hogy és így a 2. lemma szerint . Ekkor . Vegyük észre, hogy két nulla normájú számhármas összegére bontható: . Az 1. lemma szerint ezekből csak négyzetszámokat tartalmazó számhármasokba juthatunk el, így az út lépéseit a tagokra végrehajtva az | |
előállítást kapjuk, ahonnan , és ezt akartuk bizonyítani.
A 2. lemma algoritmusa elő is állít egy ilyen felbontást. Ha az út lépéseit fordított sorrendben hajtjuk végre az és a tagokból indulva, akkor megkapjuk az (és persze a másik két koordináta) felbontását két négyzetszám összegére.
Példa. , ugyanis . A megfelelő számhármas . Ekkor
Feladatok. Bizonyítsuk be, hogy egy alakú szám minden osztója alakú. (Segítség: .)
Bizonyítsuk be, hogy esetén vagy alakú. (Segítség: Ekkor két osztály van. vagy .)
Legyen és . Bizonyítsuk be, hogy ekkor vagy .
I. megjegyzés. . Hogy melyik felbontást találjuk meg, az esetén -től függ: esetén az elsőt, esetén pedig a másodikat.
II. megjegyzés. Tételünk egyszerű következményeként adódik az a látszólag erősebb állítás is, hogy ha , akkor minden osztója előáll két négyzetszám összegeként. Két ,,standard'' összefüggésből ugyanis nyomban adódik, hogy ha , akkor -nek van alakú többszöröse. Ismeretes, hogy ha , akkor léteznek olyan , egészek, amelyekre . Az Euler‐Lagrange azonosság szerint ekkor | |
Számhármasok szétbontása
Most a számhármasok szétbontásán alapuló ötletünket fejlesszük tovább: legyen . Ekkor
Tehát
Most ezt a kicsit furcsa, de igen hasznos azonosságunkat fogjuk felhasználni a következő tétel bizonyításában.
2. tétel. Tegyük fel, hogy és . Ekkor léteznek egészek, hogy .
Bizonyítás. A bizonyítás a következő felbontáson alapul:
Ekkor , illetve a definíció szerint
Fennáll továbbá, hogy .
Alkalmazzuk a azonosságot az felbontásra:
Tehát , vagyis . Ez -ra nézve másodfokú egyenlet, amelynek létezik egész megoldása, így a diszkriminánsa négyzetszám: | |
Mivel , azért , azaz .
Ezzel bebizonyítottuk az állítást.
Végkifejlet
Ha , akkor a 2. tétel szerint léteznek , egészek, hogy . Megmutatható, hogy ennek a diofantikus egyenletnek nincs , egész megoldása és ezzel végre választ kaphatunk az A. 376. feladat kérdésére: az számhármasból nem lehet eljutni az számhármasba. Ennek részletesebb tárgyalásába nem megyünk bele, később úgy is látunk egy invariánst, amely végleg elintézi ezt a problémát.
Min múlik, hogy az diofantikus egyenletnek nincs megoldása? Az egyenletet -tel osztva kapjuk, hogy , vagyis . Az racionális szám tehát nagyon jó ,,hatásfokú'', a nevező méretéhez képest kicsiny hibájú közelítése a számnak.
Ilyen közelítések sorozata hatékony eljárásokkal állítható elő és ez a sorozat adott szám ‐ mint esetünkben a ‐ esetén lényegében egyértelműen meghatározott. A fenti egyenlet megoldása pedig tagja kell legyen ennek a -hez tartozó sorozatnak. Ennek persze végtelen sok eleme van, de ismeretes, hogy ha az elemekhez kiszámoljuk az értékeket, akkor az így előálló számok halmaza már véges! Ha pedig ellenőrizzük ezeket az értékeket, kiderül, hogy az 5 nincs közöttük!
A most vázolt eszközök vezetnek el egy az itt leírtaknál finomabb invariánshoz. Erről szól majd a cikk folytatása |
 PDF | MathML
PDF | MathML