Kezdőlap


Cím:	A 46. Nemzetközi Matematikai Diákolipmia feladatainak megoldásai
Füzet:	2005/október, 386 - 394. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Matematikai Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

A szerkesztőség

1. Adott hat pont az

A B C

egyenlőoldalú háromszög oldalain:

A_{1}

és

A_{2}

B C

oldalon,

B_{1}

és

B_{2}

C A

oldalon,

C_{1}

és

C_{2}

A B

oldalon, úgy, hogy ezek a pontok egy

A_{1} A_{2} B_{1} B_{2} C_{1} C_{2}

konvex hatszög csúcsai, amelynek az oldalai egyenlő hosszúságúak. Bizonyítsuk be, hogy az

A_{1} B_{2}

B_{1} C_{2}

és

C_{1} A_{2}

egyenesek egy ponton mennek át.

Steller Gábor megoldása. Legyen az

A_{1} A_{2} B_{1} B_{2} C_{1} C_{2}

hatszög egyenlő oldalainak hossza

x

.
Jelölje

α_{1}

α_{2}

α_{3}

β_{1}

β_{2}

β_{3}

A_{1} B_{1} A_{2}

B_{1} C_{1} B_{2}

C_{1} A_{1} C_{2}

A_{2} B_{2} B_{1}

B_{2} C_{2} C_{1}

C_{2} A_{2} A_{1}

egyenlő szárú háromszögek alapon fekvő szögeit az ábra szerint. Legyen

B_{1} C_{1}

és

B_{2} C_{2}

szakaszok metszéspontja

P

A_{1} C_{1}

és

A_{2} C_{2}

szakaszoké

Q

A_{1} B_{1}

és

A_{2} B_{2}

szakaszoké

R

Ekkor

B_{1} A_{2} C ∢ = 2 α_{1}

A_{2} B_{1} C ∢ = 2 β_{1}

C_{1} B_{2} A ∢ = 2 α_{2}

B_{2} C_{1} A ∢ = 2 β_{2}

A_{1} C_{2} B ∢ = 2 α_{3}

és

C_{2} A_{1} B ∢ = 2 β_{3}

(külső szögek). Így az

A_{2} C B_{1}

B_{2} A C_{1}

C_{2} B A_{1}

háromszögek szögeinek összegéből

2 α_{1} + 2 β_{1} = 2 α_{2} + 2 β_{2} = 2 α_{3} + 2 β_{3} = 120^{\circ}

adódik. Az

A_{1} R A_{2}

B_{1} P B_{2}

C_{1} Q C_{2}

szögek nagysága a

B_{1} R A_{2}

C_{1} P B_{2}

A_{1} Q C_{2}

háromszögek külső szögeiként éppen

α_{1} + β_{1}

α_{2} + β_{2}

α_{3} + β_{3}

, azaz mindhárom szög

60^{\circ}

-os.
Az

A_{1} B_{1} C_{1}

és

A_{2} B_{2} C_{2}

háromszögek megfelelő oldalai így

60^{\circ}

-ot zárnak be, emiatt a háromszögek megfelelő szögei egyenlők, azaz a két háromszög hasonló. Két megfelelő oldalpár arányát felírva és az oldalakat

x

-szel és a szögekkel kifejezve kapjuk, hogy

\begin{matrix} \frac{A_{1} B_{1}}{A_{2} B_{2}} = \frac{2 x \cdot cos α_{1}}{2 x \cdot cos β_{1}} = \frac{2 x \cdot cos α_{2}}{2 x \cdot cos β_{2}} = \frac{B_{1} C_{1}}{B_{2} C_{2}} . \end{matrix}

Ebből

cos α_{1} cos β_{2} = cos α_{2} cos β_{1}

, azaz

β_{i} = 60^{\circ} - α_{i}

helyettesítéssel:

\begin{matrix} cos α_{1} cos (60^{\circ} - α_{2}) = cos α_{2} cos (60^{\circ} - α_{1}) \end{matrix}

adódik. Az addíciós tétel felhasználásával rendezés után kapjuk, hogy

\begin{matrix} sin 60^{\circ} cos α_{1} sin α_{2} = sin 60^{\circ} sin α_{1} cos α_{2}, azaz tg α_{2} = tg α_{1} . \end{matrix}

Mivel

0 < α_{1}, α_{2} < 60^{\circ}

, azért

α_{2} = α_{1}

.
Ezt a számítást egy másik oldalpárra hasonlóan elvégezve kapjuk, hogy

α_{3} = α_{2} = α_{1}

. Ekkor

\begin{matrix} A_{1} B_{1} C_{1} ∢ & = 180^{\circ} - α_{2} - α_{1} - 2 β_{1} = 180^{\circ} - 2 α_{1} - 2 β_{1} = 180^{\circ} - 120^{\circ} = 60^{\circ}, \\ B_{1} C_{1} A_{1} ∢ & = 180^{\circ} - α_{3} - α_{2} - 2 β_{2} = 180^{\circ} - 2 α_{2} - 2 β_{2} = 180^{\circ} - 120^{\circ} = 60^{\circ} . \end{matrix}

Emiatt az

A_{1} B_{1} C_{1}

háromszög szabályos, így

A_{1} B_{1} = B_{1} C_{1} = C_{1} A_{1}

. Mivel

A_{2} A_{1} = A_{2} B_{1}

B_{2} B_{1} = B_{2} C_{1}

C_{2} C_{1} = C_{2} A_{1}

, az

A_{2} C_{1}

szakasz az

A_{1} B_{1}

szakasznak,

B_{2} A_{1}

B_{1} C_{1}

-nek,

C_{2} B_{1}

C_{1} A_{1}

-nek felező merőlegese. Az

A_{1} B_{2}

B_{1} C_{2}

C_{1} A_{2}

szakaszok így az

A_{1} B_{1} C_{1}

háromszög oldalfelező merőlegesei, emiatt valóban egy ponton mennek át.

2. Legyen

a_{1}, a_{2}, ...

egész számoknak egy olyan sorozata, aminek van végtelen sok pozitív tagja és végtelen sok negatív tagja is. Tudjuk, hogy minden pozitív egész

n

-re az

a_{1}, a_{2}, ..., a_{n}

számok

n

-nel osztva

n

különböző maradékot adnak. Bizonyítsuk be, hogy minden egész szám pontosan egyszer fordul elő a sorozatban.

Mánfay Máté megoldása. Először azt mutatjuk meg, hogy a sorozat elemei különbözők. Ha ugyanis valamilyen

n < m

esetén

a_{n} = a_{m}

, akkor a sorozat első

m

eleme nem alkothat teljes maradékrendszert mod

m

. Így minden egész szám legfeljebb egyszer szerepel az

{a_{n}}

sorozatban.
Legyen most

m \geq 2

egész és tekintsük a sorozat első

m

eleme közül a legnagyobbikat: legyen ez

a_{p}

; és a legkisebbiket: legyen ez

a_{q}

; jelöljük továbbá az

a_{p} - a_{q} > 0

különbséget

d

-vel. Mint láttuk, az első

m

elem között nincsenek egyenlők, azért

d \geq m - 1

. Másfelől persze

d = a_{p} - a_{q}

miatt

a_{p} \equiv a_{q} mod d

is fennáll, így ha még

d \geq m

is teljesül, akkor a sorozat első

d

eleme nem alkot teljes maradékrendszert mod

d

.
Ebből következik, hogy

d = m - 1

, a sorozat első

m

eleme

m

darab különböző egész, amelyek legnagyobbika és legkisebbike között pontosan

m - 1

a különbség: az első

m

elem tehát

m

darab szomszédos egész szám valamilyen sorrendben. Másképpen fogalmazva: az első

m

elem minden

m

-re egy ,,intervallumot'' alkot. Ha egy ilyen halmaz tartalmaz két egész számot, akkor bármely köztük lévő egészt is tartalmazza.
Legyen most már

k

tetszőleges egész szám. Mivel a sorozat végtelen sok pozitív és végtelen sok negatív számot tartalmaz, van

k

-nál nagyobb és

k

-nál kisebb eleme is. A fentiek szerint pedig ekkor a

k

számot is tartalmaznia kell.

3. Legyenek

x

y

z

pozitív valós számok, amelyekre teljesül

x y z \geq 1

. Bizonyítsuk be, hogy fennáll az

\begin{matrix} \frac{x^{5} - x^{2}}{x^{5} + y^{2} + z^{2}} + \frac{y^{5} - y^{2}}{y^{5} + z^{2} + x^{2}} + \frac{z^{5} - z^{2}}{z^{5} + x^{2} + y^{2}} \geq 0 \end{matrix}

egyenlőtlenség.

Paulin Roland megoldása. A bizonyítást több lépésben végezzük el. Először azt mutatjuk meg, hogy elegendő arra az esetre igazolni az állítást, ha az

x

y

z

számok szorzata 1. Az

s = x^{2} + y^{2} + z^{2}

jelöléssel a bal oldal

\begin{matrix} b (x, y, z) = \frac{x^{5} - x^{2}}{s + (x^{5} - x^{2})} + \frac{y^{5} - y^{2}}{s + (y^{5} - y^{2})} + \frac{z^{5} - z^{2}}{s + (z^{5} - z^{2})} \end{matrix}

alakba írható. Az első tagot tovább alakítva

\begin{matrix} \frac{x^{5} - x^{2}}{s + (x^{5} - x^{2})} = 1 - \frac{s}{s + (x^{5} - x^{2})} . \end{matrix}

x

y

z

-t rendre megszorozzuk

c

-vel, akkor az első tag így alakul:

\begin{matrix} 1 - \frac{c^{2} s}{c^{2} s + (c^{5} x^{5} - c^{2} x^{2})} = 1 - \frac{s}{s + (c^{3} x^{5} - x^{2})} . \end{matrix}

0 < c \leq 1

, akkor

c^{3} x^{5} - x^{2} \leq x^{5} - x^{2}

, tehát a változókat

c

-vel szorozva a bal oldal első tagja, és ugyanígy a többi is, csökken. Ha

c = \frac{1}{\sqrt[3]{x y z}} \leq 1

, akkor olyan

x'

y'

z'

számhármast kapunk, amelyre egyrészt

x' y' z' = 1

, másrészt

b (x, y, z) \geq b (x', y', z')

. A továbbiakban a vessző jelölést elhagyjuk.
A pótlólagos feltétel révén megszüntethető a tagok fokszámában mutatkozó aszimmetria; a másodfokú tagokat

x y z = 1

-gyel szorozva minden tag ötödfokú lesz:

x^{2} = x^{3} y z

y^{2} = y^{3} z x

z^{2} = z^{3} x y

. Ezután az összeg első tagjában

x

-szel, a másodikban

y

-nal, a harmadikban pedig

z

-vel egyszerűsítve azt fogjuk igazolni, hogy

\begin{matrix} b (x, y, z) = \frac{x^{4} - x^{2} y z}{x^{4} + y^{3} z + y z^{3}} + \frac{y^{4} - y^{2} z x}{y^{4} + z^{3} x + z x^{3}} + \frac{z^{4} - z^{2} x y}{z^{4} + x^{3} y + x y^{3}} \geq 0. \end{matrix}

Vegyünk nagy levegőt és szorozzunk be a pozitív nevezőkkel! Az első tag ekkor így alakul:

\begin{matrix} B_{1} (x, y, z) & = (x^{4} - x^{2} y z) (y^{4} + x^{3} z + x z^{3}) (z^{4} + x^{3} y + x y^{3}) = & (1) \\ = (x^{7} y^{5} + z^{7} x^{5}) + (x^{5} y^{7} + z^{5} x^{7}) + x^{10} y z + (x^{8} y^{3} z- z^{8} x^{3} y) + \\ + (x^{8} y z^{3} - y^{8} z x^{3}) + x^{6} y^{3} z^{3} - x^{2} y^{5} z^{5} - x^{8} y^{2} z^{2} - y^{6} z x^{5} - \\ - z^{6} x^{5} y - x^{6} y^{4} z^{2} - x^{6} y^{2} z^{4} . \end{matrix}

Ellenőrzésképpen: a beszorzás után összesen

2 \times 3 \times 3 = 18

darab 12-edfokú tag összegét várjuk, azonban a tényezők első és utolsó tagjainak szorzata:

x^{4} y^{4} z^{4}

és

(- x^{2} y z) x z^{3} x y^{3}

kiesik. Ezért lesz végül 16 tagja az összegnek.
A bal oldal ezután a változók ciklikus cseréjével kapott kifejezések összege:

\begin{matrix} B (x, y, z) = B_{1} (x, y, z) + B_{1} (y, z, x) + B_{1} (z, x, y) . \end{matrix}

Vegyük észre, hogy (1)-ben a vastagon szedett tagok

f (x, y, z) - f (y, z, x)

típusúak: a változók ciklikus cseréje után összegezve ezek járuléka nulla. Ha

\sum_{c} f (x, y, z)

jelöli az

f (x, y, z) + f (y, z, x) + f (z, x, y)

alakú összegeket, akkor a bal oldal

\begin{matrix} B (x, y, z) & = 2 \sum_{c} (x^{7} y^{5} + x^{5} y^{7}) + \sum_{c} x^{10} y z + \sum_{c} x^{6} y^{3} z^{3} - \sum_{c} x^{5} y^{5} z^{2} - & (2) \\ - \sum_{c} x^{8} y^{2} z^{2} - \sum_{c} (x^{6} y^{5} z+ x^{5} y^{6} z) - \sum_{c} (x^{6} y^{4} z^{2} + x^{4} y^{6} z^{2}) . \end{matrix}

Azt kell igazolnunk, hogy

B (x, y, z) \geq 0

. Az ilyen típusú szimmetrikus egyenlőtlenségek bizonyításának alapvető eszköze a súlyozott számtani és mértani közép egyenlőtlenségének messzemenő általánosítása, a
Muirhead-egyenlőtlenség: Adott

x_{1}, x_{2}, ..., x_{n}

pozitív valós számokra és

α_{1} \geq α_{2} \geq ... \geq α_{n}

valós számokra legyen

S (α_{1}, α_{2}, ..., α_{n}) = \sum_{π \in S_{n}} x_{π (1)}^{α_{1}} ... x_{π (n)}^{α_{n}}

, ahol

S_{n}

{1,2, ..., n}

permutációinak a halmaza.
Ha

β_{1} \geq β_{2} \geq ... \geq β_{n}

olyan valós számok, amelyekre

\sum_{i = 1}^{n} α_{i} = \sum_{i = 1}^{n} β_{i}

, továbbá minden

0 < k < n

esetén

\sum_{i = 1}^{k} α_{i} \geq \sum_{i = 1}^{k} β_{i}

, akkor

S (α_{1}, α_{2}, ..., α_{n}) \geq S (β_{1}, β_{2}, ..., β_{n})

Megjegyzés. A tételben szereplő

α_{i}

(i = 1, ..., n)

és

β_{i}

(i = 1, ..., n)

,,kitevőhalmazokra'' a feltétel egy reláció teljesülését írja elő; jelöljük ezt így:

\begin{matrix} (α_{1}, α_{2}, ..., α_{n}) ≻ (β_{1}, β_{2}, ..., β_{n}) . \end{matrix}

A (2) bal oldalán a Muirhead-egyenlőtlenség feltételéhez képest csak a változók ciklikus permutációi révén előálló tagok szerepelnek. Vegyük észre viszont, hogy (2)-ben egyrészt a vastagon szedett összegek tagjai

f (x, y, z) + f (y, x, z)

alakúak, a további tagokban pedig két kitevő rendre egyenlő. Az első észrevétel szerint a vastagon szedett tagok a változók ciklikus permutációja után olyan 6 tagú összegeket szolgáltatnak, amelyekben a változók valamennyi permutációja szerepel. Például

\begin{matrix} \sum_{c}^{} (x^{6} y^{5} z+ x^{5} y^{6} z) = (x^{6} y^{5} z + y^{6} z^{5} x + z^{6} x^{5} y) + (x^{5} y^{6} z + y^{5} z^{6} x + z^{5} x^{6} y) . \end{matrix}

Ez pedig már éppen az

x

y

z

változókra adódó

S (6,5,1)

összeg.
A második észrevétel azt jelenti, hogy például

\begin{matrix} \sum_{c}^{} x^{10} y z = x^{10} y z + y^{10} z x + z^{10} x y = \frac{1}{2} S (10,1,1), \end{matrix}

és az egyenlő kitevőket tartalmazó további összegek is hasonlóan írhatók.
A bizonyítandó állítás ilyenformán a

\begin{matrix} (2 S (7,5,0) - S (6,5,1) - S (6,4,2)) + \\ + \frac{1}{2} (S (10,1,1) + S (6,3,3) - S (5,5,2) - S (8,2,2)) \geq 0 \end{matrix}

alakot ölti. Mivel

(7,5,0) ≻ (6,5,1)

és

(7,5,0) ≻ (6,4,2)

, azért a fenti összeg első tagja a Muirhead-egyenlőtlenség szerint nemnegatív. Az összeg második részével zűrösebb a helyzet: egyfelől

(10,1,1) ≻ (8,2,2) ≻ (5,5,2)

, tehát az első tag egyik levonandónál sem kisebb; a második tagra viszont

S (6,3,3) \leq S (8,2,2)

, hiszen

(6,3,3) ≺ (8,2,2)

, illetve a tétel nem is ad lehetőséget arra, hogy

S (6,3,3)

-at és

S (5,5,2)

-t összehasonlítsuk.
A Muirhead-egyenlőtlenség annyit azért biztosít, hogy

S (8,2,2) \geq S (5,5,2)

és így az összeg második része

\begin{matrix} S (10,1,1) + S (6,3,3) - S (5,5,2) - S (8,2,2) \geq S (10,1,1) + S (6,3,3) - 2 S (8,2,2) . \end{matrix}

A jobb oldal ,,általános'' tagja

x^{10} y z + x^{6} y^{3} z^{3} - 2 x^{8} y^{2} z^{2}

alakú, ez pedig a számtani és mértani közepek egyenlőtlensége szerint valóban nem negatív. Ezzel a bizonyítást ‐ végre ‐ befejeztük.

Megjegyzés. A nem beavatott olvasó némi csalódást érezhet, hogy a magyar csapat számára legnehezebbnek bizonyult feladatot végül is egy nem túl közismert ,,nagyágyú'' segítségével morzsolta fel a szerző. Tény, ami tény: Paulin Roland erre a megoldásra kapta meg egyedüli magyar versenyzőként a maximális 7 pontot. (A magyar csapat további tagjai egyetlen pontot sem szereztek ezen a feladaton és ez nem róluk árulkodik, hanem a feladatról.)
Következő számunkban közöljük a moldovai Iurie Boreico szépségdíjas megoldását, valamint a hivatalos megoldást is. A fentiekben alaposan kihasznált Muirhead-egyenlőtlenségre pedig e számunk 394. oldalán visszatérünk.

4. Tekintsük azt az

a_{1}, a_{2}, ...

sorozatot, amit az

\begin{matrix} a_{n} = 2^{n} + 3^{n} + 6^{n} - 1 (n = 1,2, ...) \end{matrix}

képlet definiál. Határozzuk meg az összes olyan pozitív egész számot, ami relatív prím a sorozat minden tagjához.

Erdélyi Márton megoldása. Egy pozitív egész akkor és csak akkor relatív prím a sorozat valamennyi elemével, ha a prímosztóinak megvan ez a tulajdonsága. Elegendő tehát a feladat kérdését a prímszámokra megvizsgálni. Megmutatjuk, hogy minden

p

prímszám osztója a sorozat valamelyik tagjának. Ebből következik, hogy a feladat egyetlen megoldása az 1, amely természetesen minden taghoz relatív prím.
Ha

p ∣ 6

, akkor

p ∣ a_{2} = 4 + 9 + 36 - 1 = 48

. Ha

(p; 6) = 1

, akkor a kis Fermat-tétel szerint

2^{p - 1} \equiv 3^{p - 1} \equiv 6^{p - 1} \equiv 1 (mod p)

. Ekkor

p > 3

miatt

a_{p - 2}

értelmes és

\begin{matrix} 6 a_{p - 2} & = 6 \cdot 2^{p - 2} + 6 \cdot 3^{p - 2} + 6 \cdot 6^{p - 2} - 6 = 3 \cdot 2^{p - 1} + 2 \cdot 3^{p - 1} + 6^{p - 1} - 6 \equiv \\ \equiv 3 + 2 + 1 - 6 = 0 (mod p) . \end{matrix}

Így

p ∣ 6 a_{p - 2}

és mivel

(p; 6) = 1

, azért

p ∣ a_{p - 2}

. Minden

p

prímszámnak találtunk tehát többszörösét a sorozat elemei között, a bizonyítást befejeztük.

5. Az

A B C D

konvex négyszög

B C

és

A D

oldalai egyenlő hosszúságúak és nem párhuzamosak. Legyenek

E

, illetve

F

rendre a

B C

, illetve

A D

oldal olyan belső pontjai, amikre

B E = D F

teljesül. Az

A C

és

B D

egyenesek metszéspontja

P

, a

B D

és

E F

egyenesek metszéspontja

Q

, az

E F

és

A C

egyenesek metszéspontja

R

. Tekintsük az összes

P Q R

háromszöget, amint

E

és

F

változnak. Bizonyítsuk be, hogy ezen háromszögek körülírt köreinek van egy

P

-től különböző közös pontja.

Strenner Balázs megoldása. Legyen

X

A C

és a

B D

átlók felező merőlegeseinek a metszéspontja. A négyszög konvex, azért az

X

metszéspont létrejön. Megmutatjuk, hogy az

X

a keresett pont, azaz

P Q X R

E, F

pontok minden megfelelő választása mellett húrnégyszög.
Az

X

választása miatt

A X = X C

és

B X = X D

. A feltétel szerint

B C = A D

, azért

B C X ▵ ≅ D A X ▵

. Ebből következik, hogy

B X C ∢ = D X A ∢

, tehát

B X D ∢ = C X A ∢

(1. ábra).

1. ábra

Az egyenlő szárú

B X D

és

C X A

háromszögek

X

-nél lévő szárszöge tehát egyenlő, így a két háromszög hasonló. Van tehát olyan

X

középpontú

φ = B X C ∢

szögű

F

forgatva nyújtás, amely a

B X D

háromszöget a

C X A

háromszögbe viszi. Ez a hasonlósági transzformáció a

B D

szakaszt a

C A

szakaszba viszi, miközben a

B D

adott arányú osztópontjait a

C A

megfelelő arányú osztópontjaiba képezi le. Megmutatjuk, hogy a

Q

képe

R

, azaz

\begin{matrix} \frac{B Q}{Q D} = \frac{C R}{R A} . \end{matrix}

(1)

Írjuk fel a szinusztételt a

B E Q

és a

Q D F

háromszögekben (2. ábra):

\begin{matrix} \frac{B Q}{sin B E Q ∢} = \frac{B E}{sin B Q E ∢} és \frac{Q D}{sin Q F D ∢} = \frac{D F}{sin D Q F ∢} . \end{matrix}

Mivel

B E = D F

és

B Q E ∢ = D Q F ∢

, azért innen azt kapjuk, hogy

\begin{matrix} \frac{B Q}{Q D} = \frac{sin B E Q ∢}{sin Q F D ∢} . \end{matrix}

(2)

Hasonlóan kapjuk az

C E R

és az

R F A

háromszögekből, hogy

\begin{matrix} \frac{C R}{R A} = \frac{sin C E R ∢}{sin R F A ∢} . \end{matrix}

(3)

Mivel

C E R ∢

és

Q E B ∢

, illetve

R F A ∢

és

Q F D ∢

kiegészítő szögek, azért a szinuszuk páronként egyenlő; (2) és (3) jobb oldala tehát egyenlő, innen pedig már következik (1).

2. ábra

Q

képe

R

, akkor

Q X R ∢ = φ

, a forgatva nyújtás szöge. Mivel pedig

F

B D

szakaszt a

C A

-ba viszi, a két egyenes hajlászöge is ennyi,

B P C ∢ = φ

. Ez pedig éppen azt jelenti, hogy a

P

Q

X

R

pontok egy körön vannak, és ezt akartuk bizonyítani.

Megjegyzés: A feladatban a

P

Q

R

pontok különbözőek. Ha nem ez a helyzet, azaz

E F

áthalad az átlók

P

metszéspontján, akkor

F

Q

-t önmagába viszi és mivel nem helybenhagyás, hiszen

B D

-t

C A

-ba viszi, azért

Q = X

, a négy pont egybeesik. Ez a pont így mindkét átlót felezi, a négyszög átlói felezik egymást. A négyszög tehát paralelogramma, ezt viszont a feltétel kizárja.

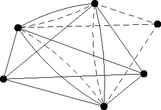
6. Egy matematikaversenyen

6

feladatot kellett a versenyzőknek megoldani. Bármelyik két feladatra igaz az, hogy a versenyzők

\frac{2}{5}

részénél többen oldották meg mindkét feladatot. Senki nem oldotta meg mind a

6

feladatot. Bizonyítsuk be, hogy volt legalább

2

olyan versenyző, aki pontosan

5

feladatot oldott meg.

Jankó Zsuzsanna megoldása. Legyen a versenyzők száma

n

és tegyük fel, hogy

a_{i}

versenyző oldott meg pontosan

i

feladatot,

i = 0,1,2,3,4,5

. A feltétel szerint minden egyes feladatpárt legalább

⌈ \frac{2 n + 1}{5} ⌉ > \frac{2 n}{5}

versenyző oldott meg. A 6 feladatból 15 pár alkotható, azért a versenyzők által megoldott feladatpárok számának

P

összege legalább

15 ⌈ \frac{2 n + 1}{5} ⌉

. Ez az érték

6 n + d

alakú, ahol a

d

attól függ, milyen maradékot ad

n

az 5-tel osztva. Ha

n = 5 k + r

, akkor

⌈ \frac{2 n + 1}{5} ⌉ = 2 k + ⌈ \frac{2 r + 1}{5} ⌉

és így

\begin{matrix} 15 ⌈ \frac{2 n + 1}{5} ⌉ = 30 k + 15 ⌈ \frac{2 r + 1}{5} ⌉ = {\underset{︸}{30 k + 6 r}}_{6 n}^{} + {\overset{}{\overset{︷}{15 ⌈ \frac{2 r + 1}{5} ⌉ - 6 r}}}_{}^{d} . \end{matrix}

r

lehetséges értékeit behelyettesítve kapjuk, hogy

\begin{matrix} r & 0 & 1 & 2 & 3 & 4 \\ d & 15 & 9 & 3 & 12 & 6 \end{matrix}

P

összeg az

a_{i}

mennyiségek felhasználásával pontosan is meghatározható. Ha

i \geq 2

és egy

X

versenyző

i

feladatot oldott meg, akkor

(\binom{i}{2})

olyan pár van, amelynek

X

mindkét feladatát megoldotta. Az

a_{i}

darab

i

-feladatos versenyző tehát

a_{i} \cdot (\binom{i}{2})

-vel járul hozzá a

P

összeghez:

\begin{matrix} P = a_{2} + a_{3} \cdot (\binom{3}{2}) + a_{4} \cdot (\binom{4}{2}) + a_{5} \cdot (\binom{5}{2}) = a_{2} + 3 a_{3} + 6 a_{4} + 10 a_{5} . \end{matrix}

(1)

Láttuk, hogy

P \geq 6 n + d

. Mivel

n = a_{0} + a_{1} + a_{2} + a_{3} + a_{4} + a_{5}

és

a_{i} \geq 0

, azért

6 n \geq a_{2} + 3 a_{3} + 6 a_{4} + 6 a_{5}

. Becsléseinket egybevetve

\begin{matrix} P = a_{2} + 3 a_{3} + 6 a_{4} + 10 a_{5} \geq 6 n + d \geq a_{2} + 3 a_{3} + 6 a_{4} + 6 a_{5} + d . \end{matrix}

(2)

Innen azt kapjuk, hogy

4 a_{5} \geq d

, azaz a

d

lehetséges értékeit figyelembe véve

\begin{matrix} a_{5} \geq \frac{d}{4} > 1, ha r \neq 2. \end{matrix}

Mivel

a_{5}

egész szám, így valóban legalább 2, ha

r \neq 2

. Abban az esetben kell még igazolnunk a feladat állítását, ha

n = 5 k + 2

. Ilyenkor

d = 3

és a fenti becslés csak annyit ad, hogy

a_{5} \geq \frac{3}{4}

, azaz

a_{5} \geq 1

. Megmutatjuk, hogy a feladat feltételei esetén

a_{5}

nem lehet 1, azaz ebben az esetben is legalább 2.
Tegyük fel, indirekt módon, hogy

n = 5 k + 2

versenyző a feltételekben leírtak szerint szerepelt és közülük összesen egyvalaki oldott meg pontosan 5 feladatot. Ekkor

d = 3

a_{5} = 1

, a (2) becslés pedig így alakul:

\begin{matrix} a_{2} + 3 a_{3} + 6 a_{4} + 10 & \geq 6 n + d = 6 (a_{0} + a_{1} + a_{2} + a_{3} + a_{4} + 1) + 3, ahonnan \\ 4 & \geq 6 a_{0} + 6 a_{1} + 5 a_{2} + 3 a_{3} + 3, \end{matrix}

ami csak úgy lehetséges, ha

a_{0} = a_{1} = a_{2} = a_{3} = 0

, hiszen az

a_{i}

mennyiségek nemnegatív egészek. Feltevésünk szerint most

a_{5} = 1

, így végül

a_{4} = n - 1

. Ekkor (1)-ből azt kapjuk, hogy

\begin{matrix} P = (n - 1) \cdot (\binom{4}{2}) + (\binom{5}{2}) = 6 n + 4 = 1 + 15 \cdot \frac{2 n + 1}{5} . \end{matrix}

(3)

Most

n \equiv 2 (mod 5)

, tehát

\frac{2 n + 1}{5} = ⌈ \frac{2 n + 1}{5} ⌉

. Mivel a 15 feladatpár mindegyikét legalább ennyi versenyző oldotta meg, a feladatpárok szerint (3)-ban kiszámolt összeg pedig pontosan 1-gyel nagyobb, mint ennek a 15-szöröse, azért pontosan egy olyan feladatpár van, amelyet

\frac{2 n + 1}{5}

-nél többen oldottak meg, mégpedig pontosan eggyel többen.
Ábrázoljuk a verseny kimenetelét egy 6-pontú

G

gráfban. A gráf csúcsai feleljenek meg az egyes feladatoknak és két csúcsot annyiszor kössünk össze éllel, ahány résztvevő megoldotta a megfelelő két feladatot. Az ábra egy olyan esetet mutat, ahol

n = 2

és így egy-egy résztvevő oldott meg 4, illetve 5 feladatot. Gráfunk tehát egy-egy teljes öt-, illetve négypontú egyszerű gráf uniója. Mielőtt még ellenpéldát kezdenénk keresgélni, gondoljuk meg, hogy a teljes ötös megrajzolása után a hatodik csúcs még öt másikkal nincs összekötve, ezeket a hiányzó éleket pedig nem lehet egyetlen teljes négyessel lefogni. Sérül tehát az a feltétel, hogy bármely két feladatot több mint

2 \cdot \frac{2}{5}

, azaz legalább egy versenyző megoldott.

A fentiek szerint

G

általában egy teljes ötös és

(n - 1)

teljes négyes uniója. Amíg csak teljes négyeseket rajzolunk a hat pontra, addig minden csúcs foka hárommal vagy nullával nő, azért a

G

csúcsainak a foka modulo 3 egyenlő a hat pontra rajzolt teljes ötös megrajzolása után kapott hatpontú gráf csúcsainak a fokával: öt fokszám 1, a hatodik pedig 0 maradékot ad 3-mal osztva.
Ez viszont nem lehetséges. Láttuk ugyanis, hogy most egyetlen olyan feladatpár van, amelyet eggyel többen oldottak meg, mint a többi 14-et. Gráfunk csúcsainak fokszámai tehát kétfélék ugyan modulo 3, de az egyik érték kétszer lép fel ‐ abban a két csúcsban, amelyeknek megfelelő feladatpárt

1 + \frac{2 n + 1}{5}

résztvevő oldott meg ‐ a másik pedig a további csúcsokban, tehát négyszer. Ezzel a bizonyítást befejeztük.