Cím: Beszámoló az Arany Dániel matematikai tanulóversenyről - II. forduló feladatainak megoldása
Füzet: 1951/december, 171 - 179. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kezdők feladatai:
1. Hozzuk lehető legegyszerűbb alakra az

1(x-1)(x-y)(x-z)+1(y-x)(y-1)(y-z)+1(z-x)(z-y)(z-1)


kifejezést.
 

I. megoldás. Vonjuk össze először az első két törtet:
1(x-1)(x-y)(x-z)+1(y-x)(y-1)(y-z)=-(y-1)(y-z)-(x-1)(z-x)(x-1)(y-1)(x-y)(y-z)(z-x)==x2-y2-z(x-y)-x+y(x-1)(y-1)(x-y)(y-z)(z-x)=x+y-z-1(x-1)(y-1)(y-z)(z-x).


Adjuk ehhez hozzá a harmadik törtet:
x+y-z-1(x-1)(y-1)(y-z)(z-x)+1(z-x)(z-y)(z-1)==(z-1)(x+y-z-1)-(x-1)(y-1)(x-1)(y-1)(z-1)(y-z)(z-x)


A számlálót így alakíthatjuk át:
z(x+y)-(x+y)-z2+1-(xy-x-y+1)==-xy+xz+yz-z2=-x(y-z)+z(y-z)=(y-z)(z-x).


E két tényező szerepel a nevezőben is s így lehet velük egyszerűsíteni. A kifejezés legegyszerűbb alakja tehát
1(x-1)(y-1)(z-1).

II. megoldás: Vonjuk össze mindhárom törtet. Az
-(y-1)(z-1)(y-z)-(z-1)(x-1)(z-x)-(x-1)(y-1)(x-y)(x-1)(y-1)(z-1)(x-y)(y-z)(z-x)
kifejezést kapjuk. Miután a nevező elsőfokú kifejezések szorzata, egyszerűsíteni csak úgy lehet, ha a tényezők valamelyikével osztható a számláló is. Ha a számláló osztható valamelyik tényezővel, akkor olyan helyettesítésre, melyre a kérdéses tényező 0 lesz, 0 kell legyen a számláló is. Könnyű látni, hogy ha x, y, vagy z helyett 1-et teszünk, akkor a számláló nem 0. Ha ellenben x helyébe y-t, vagy z-t helyettesítünk, akkor mindkét esetben 0 lesz a számláló is. Tekintsük most a számlálót úgy, mint x-nek polinomját, melyben y és z határozott mennyiségek. Ekkor x-nek másodfokú polinomja a számláló, melynek két nulla helye x=y és x=z. Tudjuk, hogy egy másodfokú polinom mindig gyöktényezős szorzatként írható. Ezek szorzatát meg kell még szorozni x2 együtthatójával. x2-es tagot a számláló második és harmadik tagjából kapunk, z-1 és -(y-1) együtthatóval, tehát x2 együtthatója z-y. A számláló tehát így alakítható szorzattá:
(z-y)(x-y)(x-z)=(x-y)(y-z)(z-x).
Ez megegyezik a nevező második három tényezőjével. Így az egész számlálóval lehet egyszerűsíteni és a kifejezés ilyen alakban írható:
1(x-1)(y-1)(z-1).

2. Az n szám, mely pozitív egész értékeire osztható és melyekre nem osztható 27-2-vel, az
n7-n
kifejezés?
 

I. megoldás: 27-2=126=2⋅32⋅7. Ha megmutatjuk, hogy egy kifejezés 2-vel, 32-nel és 7-tel osztható, akkor következik, hogy osztható a szorzatukkal is, mivel e számoknak nincsenek közös tényezői. n7-n mindig páros, mert vagy mindkét tag, vagy egyik sem páros.
Hárommal osztva n vagy 1-et, vagy 2-t ad maradékul, vagy osztható 3-mal. Ha n osztható 3-mal, akkor n7-n=n(n6-1) 3-nak csak azzal a hatványával osztható, mint maga az n, mert n6 osztható 3-mal és így n6-1 nem lehet 3-mal osztható.
Ha tehát n osztható 3-mal, de 9-cel nem, akkor n7-n nem osztható 27-2-vel.
3-mal nem osztható szám 3-ik hatványáról 9-cel való oszthatóság szempontjából is tudunk valamit mondani, ugyanis ha a szám 1-et ad maradékul 3-mal osztva, akkor ilyen alakú 3k+1, ha pedig 2-t ad maradékul, akkor 3l+2 alakban írható. Ezek köbe:
(3k+1)3=27k3+27k2+9k+1=9K+1,(3l+2)3=27l3+54l2+36l+8=9L-1,
ahol K és L egész szám. Hogy ezt felhasználhassuk, a vizsgálandó kifejezést így alakíthatjuk át
n7-n=n(n6-1)=n((n3)2-1)=n(n3+1)(n3-1).
Innen az előzők felhasználásával látjuk, hogy 3k+1 alakú számokra az n3-1 tényező, 3l+2 alakúra viszont n3+1 osztható 9-cel.
Nézzük végül meg, hogy mikor osztható a kifejezés 7-tel. Ha n osztható 7-tel, akkor az egész kifejezés is. Ha n nem osztható 7-tel, akkor 7-tel osztva 7-nél kisebb maradékot ad, vagyis ilyen alakú n=7r+s, ahol s=1,2,3,4,5 vagy 6. Számítsuk ki ismét a szám harmadik hatványát
(7r+s)3=73r3+3⋅72⋅r2s+3⋅7⋅rs2+s3=7R+s3,
ahol R ismét valamilyen egész szám. s3 lehetséges értékei 1, 8, 27, 64, 125, 216. Az első második és negyedik érték egy-egy 7-tel osztható szám után következik, tehát ha s=1,2, vagy 4, akkor n3-1 osztható 7-tel. Ha viszont s=3,5 vagy 6, akkor s3 eggyel kisebb egy 7-tel osztható számnál, tehát ez esetben n3+1 osztható 7-tel. n7-n tehát minden egész n-re osztható 7-tel.
Ezzel láttuk, hogy 27-2 minden egész n-re osztója az n7-n értéknek, kivéve, ha n osztható 3-mal, de nem osztható 9-cel.
 

II. megoldás: Sok oszthatósági tulajdonságot tudunk leolvasni, ha szomszédos egész számok szorzatáról van szó. Kíséreljük meg ilyen alakra hozni a vizsgálandó kifejezést:
N=n7-n=n(n6-1)=n(n3-1)(n3+1)==n(n-1)(n2+n+1)(n+1)(n2-n+1).


A két másodfokú kifejezés már nem bontható hasonló tényezők szorzatára, de nem sokkal különbözik a már talált tényezőkkel szomszédos számok: n-3, n-2, n+2, n+3 közül alkalmasan kiválaszthatók szorzatától:
n2-n+1=(n-3)(n+2)+7,n2+n+1=(n+3)(n-2)+7.
Így
N=(n-1)n(n+1)[(n-3)(n+2)+7][(n+3)(n-2)++7]=(n-3)(n-2)(n-1)n(n+1)(n+2)(n+3)++7(n-1)n(n+1)[(n-3)(n+2)+(n+3)(n-2)+7].


Az utolsó tényezőt polinommá alakítva így írható:
2n2-5=2(n-1)(n+1)-3.
Itt most már az első tag hét egymásutáni szám szorzata. Ha n egész szám, ezek közt legalább három egymásutáni páros szám van (ezek közül pedig legalább egy 4-gyel is osztható). A szorzat tehát páros (2-nek legalább is negyedik hatványával osztható). A hét tényező közül legalább két 3-mal osztható és pontosan egy 7-tel osztható kell hogy legyen. A szorzat tehát osztható 2⋅32⋅7-tel. (Bizonyosan van a hét tényező közt 5-tel osztható is, s így ez a szorzat mindig osztható 24⋅32⋅5⋅7=2⋅3⋅4⋅5⋅6⋅7-tel is.)
A második tagban hasonlóan látható, hogy a három egymásutáni szám szorzata mindig osztható 6-tal, s így a szögletes zárójel előtti kifejezés mindig osztható 2⋅3⋅7-tel. Azt kell tehát csak megnézni, hogy a 2(n-1)(n+1)-3 kifejezés milyen n-re osztható 3-mal.
Ha n osztható 3-mal, akkor ez a kifejezés nem osztható 3-mal. Ha n nem osztható 3-mal, akkor nyilván az első tag valamelyik tényezője osztható 3-mal, s így az egész kifejezés is. Az n7-n kifejezés tehát mindig osztható 27-2-vel, csak akkor nem, ha n osztható 3-mal, de nem osztható 9-cel.
 

3. Rajzoljunk egy kört, húzzunk egy egyenest és tűzzünk ki az egyenesen két pontot. Szerkesszük meg az egyenesen azt a pontot, amely körül elforgatható az egyenes úgy, hogy mindkét kitűzött pont egyidejűleg a körre kerüljön.
 

I. megoldás: Ha a keresett pont körül nem csak az egyenest forgatjuk, hanem a két kitűzött ponton át az adott körrel, egyenlő kört rajzolunk és ezt is elforgatjuk, akkor ez éppen az adott körre forgatható. Ez esetben azonban a forgatás középpontja rajta lesz a két kör középpontjának távolságát felező merőlegesen. Ez az egyenes metszi tehát ki a keresett pontot az adott egyenesből.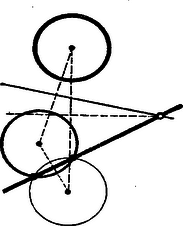
 
 

A szerkesztés elvégezhető, ha a két pont távolsága nem nagyobb az adott kör átmérőjénél. Ezen kívül akkor sincs megoldása a feladatnak, ha a szerkesztéshez felhasznált felező merőleges párhuzamos az adott egyenessel. Ez akkor következik be, ha az adott kör középpontjából az adott egyenesre bocsátott merőleges talppontja felezi a két kitűzött pont távolságát. Ekkor párhuzamos eltolással vihető a két pont egyidejűleg a körre.
Látszólag két megoldása van a feladatnak, mert a kitűzött pontokon át két kívánt nagyságú kör rajzolható. E két kör szimmetrikus az adott egyenesre nézve. Így a kétféle szerkesztésnél használható felező merőlegesek és az adott egyenes oldalfelező merőlegesei annak a háromszögnek, melyet az adott kör és a két segédkör középpontjai alkotnak. E három egyenes tehát egy pontban találkozik. Így a kétféle szerkesztésben használt felező merőlegesek ugyanazt a pontot metszik ki az adott egyenesből.
 

II. megoldás: A keresett pont hatványa az elforgatott egyenesen számítva úgy nyerhető, mint a keresett ponttól a kitűzött pontokig mért távolságok szorzata. Ugyanekkora a hatványa a keresett pontnak bármely a kitűzött pontokon átmenő körre nézve. Így egy ilyen körnek és az adott körnek a közös hatványvonala metszi ki a keresett pontot az adott egyenesből. Célszerű olyan kört rajzolni az adott pontokon át, amely metszi az adott kört.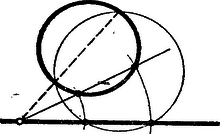
 
 

Az előbbi megoldás is tekinthető ilyen típusú megoldásnak, mert az ott használt középmerőleges a két egyenlő sugarú kör hatványvonala.
 


Haladók feladatai:
 

1. Legyenek m és n adott nullától különböző pozitív számok. Oldjuk meg az
xy=yx,xm=yn
egyenletrendszert.
 

I. megoldás: Emeljük az első egyenletet m-edik, a másodikat y-adik hatványra:
xmy=ymx,xmy=yny.
Innen
ymx=yny.
Ez az egyenlőség úgy állhat fenn, hogy vagy y=1, vagy mx=ny.
Az első esetben a kiindulási egyenletből adódik, hogy x=1. A második esetben a nyert egyenletből x értékét a második kiindulási egyenletbe helyettesítve
(nm)mym=yn,y=(nm)mn-m;x=nmy=(nm)nn-m.

Az eredményeket az első egyenlet baloldalába helyettesítve
x=(nm)nn-m(nm)mn-m=(nm)mn-m⋅nm(nm)nn-m=(nm)nn-m⋅(nm)nn-m=yx.



A nyert eredmények tehát valóban megoldásai az egyenletrendszernek.
 

II. megoldás: Az első egyenletnek könnyen előállíthatjuk az összes megoldásait: Ha x=1, akkor y=1. Ha x≠1, akkor vegyük mindkét oldalnak logaritmusát (nem lényeges, hogy milyen alapszámra vonatkozóan)
ylogx=xlogy,  azaz  yx=logylogx.
Jelöljük ezt a hányadost t-vel, azaz y=tx és a vizsgált egyenletből
xtx=xxtx,
és innen
xt=xt,x=t1t-1,y=tx=ttt-1,
feltéve, hogy t≠1. Utóbbi esetben x=y és ez mindig kielégíti az egyenletet. Így az első egyenlet összes megoldásai
x=yésx=t1t-1,y=ttt-1.
Ezeket a második egyenletbe helyettesítve xm=xn csak akkor állhat fenn, ha x=1, ekkor y=1.
A második értékpárt behelyettesítve
tmt-1=tntt-1,ahonnanm=nt,azazt=mn,
és ezt behelyettesítve x és y kifejezésébe, éppen az előbbi megoldásokat kapjuk.
 

2. Szorozzuk meg a téglatest egyes oldallapjainak területét a kerületükkel. Bizonyítsuk be, hogy az így keletkezett hat mennyiség összege legalább akkora, mint a test térfogatának 24-szerese.
 

I. megoldás: Jelöljük a test éleinek hosszát a, b, c-vel. Ekkor a bebizonyítandó egyenlőtlenség
2ab⋅2(a+b)+2bc⋅2(b+c)+2ca⋅2(a+c)≧24abc,
azaz 24-gyel osztva
a2b+a2c+b2a+b2c+c2a+c2b6≧abc.
A baloldal 6 mennyiség számtani közepe, a számok mértani közepe pedig éppen abc és tudjuk (lásd pl. Aczél ‐ Surány: Egyenlőtlenségek III. évf. 3. sz.), hogy a számtani közép nagyobb a mértaninál, egyenlők csak akkor lehetnek, ha az összes számok egyenlők, ami esetünkben csak úgy következhet be, ha a=b=c.
 

II. megoldás: Előismeretek felhasználása nélkül is eljuthatunk az egyenlőtlenség bizonyításához. Azt kell megmutatnunk, hogy az egyes tagoknak a térfogattól számított eltérését megvizsgálva, ezek összege mindig pozitív.
(a2b-abc)+(a2c-abc)+(b2a-abc)+(b2c-abc)+(c2a-abc)+(c2b-abc)==ab(a-c)+ac(a-b)+ba(b-c)+bc(b-a)+ca(c-b)+cb(c-a)==(a-c)b(a-c)+(a-b)c(a-b)+(b-c)a(b-c)==(a-b)2c+(b-c)2a+(c-a)2b,


és ez a kifejezés pozitív, ha a, b, c pozitív. Nulla csak úgy lehet, ha a=b és b=c (c=a ebből következik), ami azt jelenti, hogy a három szám egyenlő.)
 

III. megoldás: Osszuk a bizonyítandó egyenlőtlenséget a pozitív abc-vel. Ekkor a baloldal rendezése után
ab+ba+bc+cb+ca+ac≧6.
De egy számnak és a reciprokának az összege legalább 2, s így valóban helyes az egyenlőtlenség, amiből abc-vel való szorzással a bizonyítandó egyenlőtlenséghez jutunk.
A felhasznált állítás így látható be:
n+1n-2=n2-2n+1n=(n-1)2n≧0,han>0,
s így
n+1n≧2.

3. Melyek azok az n egész számok, amelyekhez található olyan konvex, síklapokkal határolt test, melynek n éle van?
 

I. megoldás: Először megmutatjuk, hogy 7 kivételével minden 5-nél nagyobb élszámhoz tudunk ennyi élet tartalmazó testet szerkeszteni.
Ha az élszám páros: 2n, akkor az n-oldalú gúla megfelel a feltételnek. Minden ilyen gúlából páratlan élszámú testet kapunk, ha az egyik háromszögű lapjára még egy tetraédert illesztünk.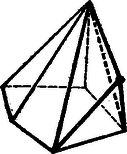
 
 

A keletkező test konvex is marad, ha a tetraéder csúcsát azon tetraéder belsejében választjuk, melyet a kiválasztott oldal és a szomszédosak meghosszabbítása alkot. Ilyen módon minden gúla élszámát 3-mal tudjuk növelni. Így 6-on fölül 7 kivételével minden páratlan élszámhoz tudunk ennyi élű testet készíteni.
Megmutatjuk azt is, hogy 7 élű test nem lehetséges. Valóban egy test lapjait határoló éleket összeszámolva az élszám 2-szeresét, esetünkben 14-et kapunk. Nem lehet minden lap háromszög, mert 14 nem osztható 3-mal. Van tehát egy legalább 4 oldalú lap és ennek éleihez csupa különböző, legalább 3 szögű lap csatlakozik.
Ekkor azonban ezen a sokszögű lapon és a hozzá csatlakozókon együtt legalább 4+4⋅3=16 élet tudnánk megszámolni, nem pedig 14-et. 7 élű test tehát nem lehetséges.
 

II. megoldás: Gúlából szerkeszthetünk olyan testet, amelyiknek csak 1 új éle van. Itt viszont az kell, hogy a gúla alapja legalább 4 oldalú legyen.
Válasszunk ki egy átlót a gúla alapján. Képzeljük ezt gumiszálból elkészítve és mozgassuk tovább úgy, hogy végpontjai továbbra is az odafutó oldaléleken maradjanak. Szemeljünk ki az alaplapon az átló mindkét oldalán egy-egy csúcsot. Ezeken a csúcsokon és az elmozdított átlón át fektessünk egy-egy síkot és metsszük el ezeket a gúla oldallapjainak meghosszabbításával.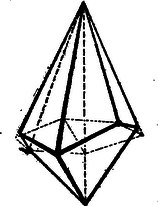
 
 

A keletkező testen az eredeti gúla alaplapjának minden élét egy új él helyettesíti. Ezen kívül él lett az elmozdított lapátlóból is. Így az élek száma 1-gyel növekedett. A 7-es élszám azonban most is kimarad, mert fel kellett tennünk, hogy az alaplap legalább 4 oldalú.
Hogy hét élű test nincs, azt így is beláthatjuk: számoljuk össze az egyes csúcsokba futó éleket. Így minden élet kétszer számolunk: mindkét végpontjánál külön, tehát 7 élű testnél 14-et kell kapnunk. Másrészt egy csúcsba legalább 3 él fut, tehát 5 csúcsa nem tehet a testnek, mert akkor a megszámolás legalább 15-öt adna. 4 csúcsú test viszont egyedül a tetraéder (három oldalú gúla), aminek 6 éle van, nem pedig 7.