Kezdőlap


Cím:	Egyenlőtlenségek (A közlemény feladatainak megoldása 1. rész)
Szerző(k):	Kántor S. , Zatykó L. , Zobor E.
Füzet:	1952/március, 51 - 57. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek
Hivatkozás(ok):	Feladatok: 1951/december: 376. matematika feladat, 1951/december: 377. matematika feladat, 1951/december: 378. matematika feladat, 1951/december: 379. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Hatványközepek közti egyenlőtlenségekkel foglalkozva láttuk, hogy a mértani közép elválasztja a pozitív és negatív kitevős hatványközepeket. Bizonyításainkat túlzott bonyodalmak elkerülésére csak racionális kitevőkre korlátoztuk. Így megmutattuk, hogy ha $r$ pozitív racionális szám és $a_{1}$ , $a_{2}$ , $...$ , $a_{k}$ tetszés szerinti pozitív számok, amelyek közt vannak különbözők, akkor

\begin{matrix} \sqrt[^{k}]{a_{1} a_{2} ... a_{k}} < \sqrt[^{r}]{\frac{a_{1}^{r} + a_{2}^{r} + ... + a_{k}^{r}}{k}}, \end{matrix}

vagy mindkét oldal 10 alapú logaritmusát véve

\begin{matrix} \frac{1}{k} (lg a_{1} + lg a_{2} + ... + lg a_{k}) < \frac{1}{r} lg \frac{a_{1}^{r} + a_{2}^{r} + ... + a_{k}^{r}}{k} . \end{matrix}

(1)

Itt a jobboldali logaritmusos kifejezést szeretnénk ‐ esetleg alkalmasan nagyítva is közben a kifejezést ‐ úgy átalakítani, hogy abban az egyes

a

-k különválasztva szerepeljenek. Nézzük tehát, milyen felső korlátot tudunk találni az

lg x

függvény számára.
Rajzoljuk meg az

lg x

függvény görbéjét. Miután a görbe alulról konkáv, meghúzva egy érintőt, a görbe mindenütt ez alatt marad. Rajzoljuk meg az

x = 1

abszcisszájú pontban az érintőt. Jelöljük ennek meredekségét

m_{10}

-zel. (Meredekségnek nevezzük az egyenes ordinátájának változását, mialatt az abszcissza egy egységnyit változik.)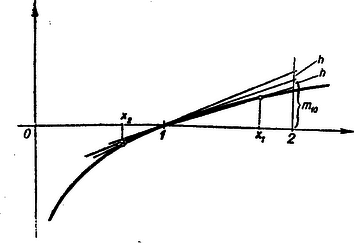

Ekkor az 1 abszcisszájú ponttól egy tetszésszerinti

x

pontig az ordináta változása

m_{10} (x - 1)

. Mivel az 1 abszcisszához az

lg 1 = 0

ordináta tartozik, így az érintő az

m_{10} (x - 1)

függvény képe. Előbbi megállapításunk tehát az algebra nyelvén így írható: ha

x \neq 1

\begin{matrix} lg x < m_{10} (x - 1) . \end{matrix}

(2)

Itt, ha

x > 1

, akkor átoszthatunk

x - 1

-gyel, ha pedig

x < 1

, akkor mind két oldal negatív lévén először

- 1

-gyel szorzunk, ellenkezőre változtatva az egyenlőtlenség jelét és aztán

1 - x

-szel osztunk. Így azt kapjuk, hogy

\begin{matrix} \frac{lg x}{x - 1} < m_{10}, ha x > 1 és \frac{- lg x}{1 - x} = \frac{lg x}{x - 1} > m_{10}, ha 0 < x < 1. \end{matrix}

Ennél az egyenlőtlenségnél többet is mondhatunk: ha elég közel választjuk

x

-et 1-hez, akkor

lg x / (x - 1)

értéke tetszésszerint kevéssel fog eltérni

m_{10}

-től. Pontosabban szólva akármilyen kis pozitív

e

számot választunk is, ehhez mindig ki tudunk jelölni az

x = 1

pont körül egy alkalmas kis szakaszt, hogy az ebbe a szakaszba eső

x

-ekre a szóbanforgó tört

e

-nél kevesebbel különbözzék

m_{10}

-től. Rajzoljuk meg ugyanis az

m_{10} - e

meredekségű egyenest is az (

1, 0

) ponton át. Ez még pontosan egy pontban metszi a görbét a konkávság miatt, mégpedig az (

1, 0

) ponttól jobbra, mert 1-nél kisebb abszcisszákra az egyenest és a görbét elválasztja az érintő. Jelöljük ennek a metszéspontját

x_{1}

-gyel, akkor nyilván

1 < x < x_{1}

-re

\begin{matrix} lg x > (m_{10} - e) (x - 1), vagyis m_{10} > \frac{lg x}{x - 1} > m_{10} - e . \end{matrix}

Hasonlóan látható, hogy az

m_{10} + e

meredekségű

(m_{10} + e) (x - 1)

egyenes egy 0 és 1 közti

x_{2}

abszcisszájú pontban metszi másodszor a görbét. Így ha

(0 <) x_{2} < x < 1

\begin{matrix} lg x > (m_{10} + e) (x - 1) \end{matrix}

és mivel

lg x

is,

x - 1

is negatív, innen, meg a fönti egyenlőtlenségből

\begin{matrix} m_{10} < \frac{lg x}{x - 1} < m_{10} + e . \end{matrix}

Így azt kaptuk, hogy ha

x_{1} > x > x_{2}

\begin{matrix} m_{10} + e < \frac{lg x}{x - 1} < m_{10} + e, \end{matrix}

(3)

ami valóban ezt jelenti, hogy ebben a szakaszban

\frac{lg x}{x - 1} e

-nél kevesebbel különbözik

m_{10}

-től. Ezt rövidebben így is írhatjuk az algebra nyelvén:

\begin{matrix} | \frac{lg x}{x - 1} - m_{10} | < e . \end{matrix}

^{$^{*}$}
A talált egyenlőtlenségeket alkalmazzuk az

x = a^{r}

értékre, ahol

a

egytől különböző pozitív szám,

r

pedig pozitív racionális szám. Ekkor azt kapjuk, hogy

\begin{matrix} r lg a < m_{10} (a^{r} - 1) . \end{matrix}

Innen, mivel

r

és

m

pozitív,

\begin{matrix} \frac{a^{r} - 1}{r} > \frac{lg a}{m_{10}} . \end{matrix}

(4)

Másrészt azt is megmutathatjuk, hogy a bal és jobb oldal különbsége tetszésszerint kicsi lesz, ha

r

-et elég kicsinek választjuk. Ha ezt bebizonyítottuk, abból utolsó állításunk azonnal következik. Láttuk ugyanis, hogy bármilyen pozitív

e

számhoz megadható olyan

x_{1} > x > x_{2}

szakasz az 1 pont körül, amelyen belül fennáll a (3) egyenlőtlenség. Még bizonyítandó állításunk éppen azt jelenti, hogy ha

a > 1

, akkor található olyan

r

pozitív racionális szám, melyre

\begin{matrix} 1 < a^{r} < x_{1}, \end{matrix}

ha pedig

0 < a < 1

, akkor található olyan

r

, amelyre

\begin{matrix} x_{2} < a^{r} < 1. \end{matrix}

Az így kiválasztott

r

-re (3) első része szerint

\begin{matrix} m_{10} - e < \frac{r lg a}{a^{r} - 1} . \end{matrix}

(5)

Osszunk még

lg a

-val:

\begin{matrix} \frac{m_{10}}{lg a} - \frac{e}{lg a} < \frac{r}{a^{r} - 1} . \end{matrix}

Innen először is leolvashatjuk, hogy

\frac{r}{a^{r} - 1}

nem lehet túl kicsiny, hiszen

e

-t tetszésszerint választhatjuk (persze más és más

e

értékhez más és más

r

érték lesz megfelelő.) Legyen pl.:

e = \frac{m_{10}}{2}

akkor azt kapjuk, hogy

\begin{matrix} \frac{1}{2} \frac{m_{10}}{lg a} < \frac{r}{e^{r} - 1} . \end{matrix}

(

5'

)

Szorozzuk másrészt az (5) egyenlőtlenséget

\frac{a^{r} - 1}{r}