Kezdőlap


Cím:	Mikor ugorjunk ki a hintából, hogy a legmesszebb érjünk a talajra?
Szerző(k):	Cserti József , Glöckler Oszvald
Füzet:	2005/november, 502 - 505. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy alkalommal, amikor e cikk egyik szerzőjének kislánya¹ a játszótéren hintázott, a következő kérdést tette fel: ,,Apa, hol kell kiugranom a hintából, hogy a legmesszebbre ugorjak?'' Ez a kérdés látszólag egyszerű, egy 10 éves kislány is megfogalmazhatja. A válasz azonban már korántsem ilyen egyszerű. Pontosabban szólva, a (tömegpontnak tekintett) kislány mozgását középiskolai ismeretek alapján le tudjuk írni, ez nem látszik bonyolult feladatnak. A nehézség abból adódik, hogy a kapott eredményből csak numerikusan tudjuk meghatározni, hogy mikor érdemes kiugrani a hintából. (A tényleges kiugrásról ‐ annak veszélyessége miatt ‐ természetesen le kell beszéljük a kisgyerekeket, de a probléma fizikáján érdemes elgondolkodnunk.)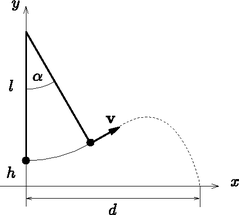
Sokan ismerik azt a tényt, hogy a különböző szögekben, de azonos kezdősebességgel elhajított kövek közül az esik a legmesszebbre, amelyiket a vízszinteshez képest $45^{\circ}$ -os szögben hajítunk el. Természetesen ebben az esetben feltételezzük, hogy a közegellenállást elhanyogolhatjuk, és a mozgás homogén gravitációs térben történik. A ,,hintás'' probléma és az elhajított kő között az a különbség, hogy a két esetben más a kezdőfeltétel. Ezért nem is várhatjuk, hogy akkor kell kiugrani a hintából, amikor a hinta kitérése éppen $45^{\circ}$ . Tegyük fel, hogy hintázás közben kialakul egy periodikus mozgás, és ekkor a hinta egy bizonyos maximális szögig lendül ki. Megmutatjuk, hogy a kiugrás ,,optimális'' szöge (amelynél a legmesszebb érünk a talajra) függ a nyugvó helyzetben lévő hintának a talajtól számított távolságától, és attól, hogy a kiugrás előtt a hinta periodikus mozgása során mekkora a hinta legnagyobb kitérésének a szöge. Látni fogjuk, hogy a fenti két paraméter függvényében ennek az optimális kiugrási szögnek is van egy felső korlátja. Ennél nagyobb szögben semmi esetre sem érdemes kiugrani a hintából, ha a lehető legmesszebb akarunk a talajra érni. Meglepő módon, ez a szög csak néhány fokkal kisebb a fent említett $45^{\circ}$ -nál.
A hintából való kiugrást modellezzük egy ingára erősített test mozgásával, amikor az inga fonala egy pillanatban elszakad! Ebben a közelítésben feltesszük, hogy a test pontszerű, és az ingát matematikai ingának tekintjük. Az 1. ábrán az $l$ hosszúságú inga fonalára kötött test mozgása látható, amikor a fonal $α$ szögnél elszakad. A test mozgását a kiugrás előtt ingamozgással, a kiugrás után ferde hajítással írhatjuk le. Tegyük fel, hogy az inga maximális kitérésének a szöge a fonál elszakadása előtt $α_{0}$ , és az inga nyugalmi helyzetében a test $h$ magasságban van a talaj fölött! Nyilvánvalóan $α \leq α_{0}$ és $h \geq 0$ . A test az 1. ábrán bejelölt $d$ tálvolságban ér talajt.

1. ábra

A fonal elszakadásakor, azaz amikor az inga kitérése

α

, a test

v

sebességének nagyságát az energiamegmaradásból számíthatjuk ki:

\begin{matrix} v = \sqrt[]{2 g l (cos α - cos α_{0})}, \end{matrix}

(1)

és a

v

sebességvektor iránya

α

szöget zár be az

x

tengellyel. A fonal elszakadása után a test a ferde hajításnak megfelelően mozog. A kezdősebességet a fenti képlet adja, a hajítás szöge a vízszinteshez képest pedig

α

. A fonal elszakadásától számított

t

idő múlva a test koordinátái (az 1. ábrán felvett koordináta-rendszerben):

\begin{matrix} x & = l sin α + v t cos α, & (2) \\ y & = h + l (1 - cos α) + v t sin α - \frac{g}{2} t^{2} . & (3) \end{matrix}

Jelöljük

t_{0}

-lal azt az időt, amennyi idő múlva a test a talajra érkezik, azaz amikor

y (t_{0}) = 0

. Ebből a feltételből a ferde hajítás során eltelt

t_{0}

időre egy másodfokú egyenletet kapunk, amelynek megoldása:

\begin{matrix} \frac{t_{0}}{\sqrt[]{2 l / g}} & = p sin α + \sqrt[]{p^{2} sin^{2} α + 1 - cos α + \frac{h}{l}}, ahol & (4) \\ p & = \sqrt[]{cos α - cos α_{0}} . & (5) \end{matrix}

Ebben a pillanatban a talajra érkezés távolsága:

d = x (t_{0})

, és a (2) és (4) egyenletek felhasználásával a következő eredményt kapjuk:

\begin{matrix} \frac{d (α)}{l} = sin α + 2 p cos α (p sin α + \sqrt[]{p^{2} sin^{2} α + 1 - cos α + \frac{h}{l}}), \end{matrix}

(6)

ahol

p

-t az (5) egyenletben definiáltuk. A

d

távolság az inga

l

hosszának egységében mérve csak az

α

és

α_{0}

szögektől, illetve a

h / l

aránytól függ, és a

0 \leq α \leq α_{0}

esetben van értelmezve. A 2. ábra a

d

távolság

α

szögtől való függését mutatja adott

α_{0}

szög és

h / l

magasság mellett. Jól látható az ábrából, hogy

d (α)

-nak maximuma van egy bizonyos

α = α^{*}

értéknél. A numerikus számításból a 2. ábra paramétereivel

α^{*} = 37, 6^{\circ}

adódik.

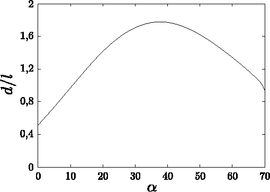2. ábra

Vajon találunk-e maximumot más

h / l

, illetve

α_{0}

értékek mellett is? Erre a 3. ábra ad választ, ahol a

d

távolságot ábrázoltuk az

α

és

α_{0}

szögek függvényében, rögzített

h / l

mellett. Látható, hogy a kapott felületen bármely állandó

α_{0}

szögnek megfelelő vonalon haladva mindig egy maximumon kell átmenni. A 3. ábrának

α_{0} = 70^{\circ}

-nál vett ,,metszete'' látható a 2. ábrán. A felület a

(0; 0)

pontból induló, emelkedő ,,hegyháthoz'' hasonlít. Mivel a

d

távolság három mennyiségnek a függvénye, csak olyan felületeket tudunk ábrázolni, amelyeknél a három változó közül egyet mindig rögzítünk. A

d

távolság további vizsgálatából kiderül, hogy a felület hasonló módon viselkedik nagyobb

h / l

aránynál is, csak még meredekebb a hegyhát. A felület jellegét a 4. ábrán látható ,,domborzati térkép'' segítségével is tanulmányozhatjuk (az egyes árnyalatok különböző

d / l

értékeknek felelnek meg). Az árnyalatok gyorsabb változása meredekebb ,,emelkedőt'' jelent.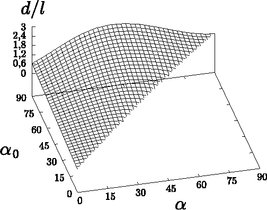

3. ábra. A

d

távolságnak (

l

egységekben mérve) az

α

és

α_{0}

szögektől való függése rögzített

h / l = 0, 1

mellett. A szögeket fokokban mértük

4. ábra. A 3. ábra ,,domborzati térképe''. A szögeket fokokban mértük

Megállapíthatjuk, hogy a talajra érkezés

d

távolsága valóban maximumot vesz fel egy bizonyos

α^{*}

értéknél, ami természetesen függ a

h / l

, illetve

α_{0}

paraméterektől. A

d (α)

függvény maximumának

α^{*}

helyét a függvény

α

szerinti deriváltjának zérushelyéből számolhatjuk ki. A (6) képlettel adott

d (α)

deriváltja meglehetősen bonyolult függvény, amelynek zérushelyét csak numerikusan tudjuk kiszámítani. Az eredmény az 5. ábrán látható, ahol az

α^{*}

szögnek

α_{0}

-tól való függését ábrázoltuk különböző

h / l

arányok mellett. A számítást kiterjesztettük arra az esetre is, amikor az inga (pontosabban a hinta) akár

α_{0} = 180^{\circ}

-ig is kilendülhet. Az ábra alapján látható, hogy az

α^{*}

szög az

α_{0}

szög monoton növekvő függvénye. Kis

α_{0}

szögekre meglehetősen gyors a függvény változása, míg nagyobb

α_{0}

értékekre a függvény ,,laposabb''. Az is világos az ábrából, hogy

h

növelésével

α^{*}

csökken, maximumát,

α^{*} \approx 42, 94^{\circ}

-ot pedig

h = 0

és

α_{0} = 180^{\circ}

-nél veszi fel. Ha a hintával csak legfeljebb

α_{0} = 90^{\circ}

-ig tudunk kilendülni, akkor a legnagyobb ugráshoz tartozó kiugrási szög felső korlátja

α^{*} (α_{0} = 90^{\circ}, h = 0) \approx 40, 99^{\circ}

5. ábra. Az

α^{*}

szögnek az

α_{0}

szögtől való függése

h / l = 0; 0, 1; 1; 100

magasságok mellett. A szögeket fokokban mértük

Összefoglalva a következő megállapításokat tehetjük. A hintából való kiugrás optimális szöge erősen függ attól, hogy nyugalomban a hinta milyen magasan van a talajhoz képest (pontosabban ezen magasság és az inga hosszának arányától), illetve, hogy hintázás közben mekkora a hinta legnagyobb kitérésének a szöge. Az optimális szöget csak numerikusan tudjuk meghatározni, ezért hintázás közben nehéz gyors választ adni a bevezetőben feltett kérdésre. Ami biztos, hogy ez az optimális szög nem lehet nagyobb

43^{\circ}

-nál. Meglepő módon ez a szög csak

2^{\circ}

-kal kisebb a ferde hajításnál ismert optimális szögnél.
Végül talán érdemes megjegyezni, hogy a fizikán túl van egy másik, nagyon fontos tanulság is. Figyeljünk oda, hogy mit kérdeznek a gyermekeink, diákjaink! Tanulhatunk tőlük.

Köszönetünket szeretnénk kifejezni Tichy Gézának és Kormányos Andornak a kézirat olvasása után javasolt hasznos tanácsaikért.

¹Glöckler Lili.