Kezdőlap


Cím:	A 36. Nemzetközi Fizikai Diákolimpia elméleti feladatai
Füzet:	2005/október, 425 - 432. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Szerencsétlenül járt műhold

A mesterséges égitestek manőverezés során leggyakrabban repülésük irányában változtatják meg sebességüket, azaz felgyorsítanak, hogy magasabb pályákra kerüljenek, vagy lefékeznek, hogy visszatérjenek a légkörbe. Ezzel szemben ebben a feladatban most kizárólag olyan pályamódosításokat vizsgálunk, melyeknek során a mesterséges égitest sugár irányú lökéssel módosítja sebességét.

A numerikus eredmények meghatározásához használd a következő értékeket: a Föld sugara

R_{T} = 6, 37 \cdot 10^{6}

m, a nehézségi gyorsulás a Föld felszínén

g = 9, 81 {m/s}^{2}

, és a sziderikus nap hosszát tekintsd

T_{0} = 24, 0

h-nak.
Tekintsünk egy

m

tömegű távközlési műholdat, mely

r_{0}

sugarú geostacionárius¹ pályán kering pontosan az Egyenlítő egy pontja fölött. A műhold manőverező hajtóművének megfelelő lökéseivel állt a pontos pályára.
Az egyes részkérdésekre kapható pontszám a feladat sorszáma után zárójelben található.
1. Kérdés.

(a)

(0,3 pont) Számold ki

r_{0}

számszerű értékét!

(b)

(0,3

+

0,1 pont) Add meg a műhold

v_{0}

sebességét, mint a

g

R_{T}

és

r_{0}

paraméterek függvényét, valamint határozd meg a sebesség számszerű értékét!

(c)

(0,4

+

0,4 pont) Határozd meg a műhold

L_{0}

perdületét (impulzusmomentumát), valamint

E_{0}

teljes mechanikai energiáját, mint a

v_{0}

m

g

és

R_{T}

paraméterek függvényét!
Amint a műhold elérte a geostacionárius pályát (lásd az F-1. ábrát), stabilizálta helyzetét, és munkára kész állapotba került, a földi irányítóközpont hibájának következtében a menőverező hajtómű rövid időre újra bekapcsolódott. A hajtómű a műholdat a Föld irányába lökte meg, és annak ellenére, hogy a földi irányítóközpont szinte azonnal reagált, és kikapcsolta a hajtóművet, a műhold sebessége egy nem kívánt

Δ v

értékkel módosult. A lökést a

β = Δ v / v_{0}

lökési paraméterrel jellemezzük. A manőver időtartama jóval rövidebb, mint a műhold keringésének bármilyen más jellemző ideje, tehát a lökés pillanatszerűnek tekinthető.

F-1. ábra

2. Kérdés. Tegyük föl, hogy

β < 1

.
2.1. (0,4

+

0,5 pont) Határozd meg az új pályát jellemző mennyiségeket², azaz a pálya poláris egyenletében szereplő

l

paramétert (semi-latus-rectum = ,,fél-merőleges-távolság'') és az

ε

excentricitást az

r_{0}

és

β

paraméterek függvényében!
2.2. (1,0 pont) Határozd meg az új pálya főtengelye és a véletlen pályamódosítás helyvektora közti

α

szöget! (A helyvektor kezdőpontja a Föld középpontja.)
2.3. (1,0

+

0,2 pont) Határozd meg a pálya földközeli, illetve földtávoli pontjának

r_{{min}_{}^{}}

, illetve

r_{{max}_{}^{}}

távolságát a Föld középpontjától, mint az

r_{0}

és

β

paraméterek függvényét, valamint add meg a kifejezések számszerű értékét

β = 1 / 4

esetén!
2.4. (0,5

+

0,2 pont) Határozd meg a módosult pálya

T

keringési idejét, mint a

T_{0}

és

β

paraméterek függvényét, és add meg a keringési idő számszerű értékét

β = 1 / 4

esetén!
3. Kérdés.
3.1. (0,5 pont) Határozd meg azt a legkisebb

β_{esc}

lökési paramétert, amely mellett a műhold elhagyja a Föld gravitációs terét!
3.2. (1,0 pont) Ebben az esetben határozd meg a műhold pályájának a Földet legjobban megközelítő pontjának

r'_{{min}_{}^{}}

távolságát a Föld középpontjától, mint az

r_{0}

paraméter függvényét!
4. Kérdés. Tegyük föl, hogy

β > β_{esc}

.
4.1. (1,0 pont) Határozd meg a

v_{0}

és

β

paraméterek függvényeként, hogy mekkora

v_{\infty}

sebessége marad a műholdnak, ha végtelen messzire eltávolodik a Földtől!
4.2. (1,0 pont) Határozd meg a végtelen távoli mozgást jellemző

b

,,impakt paramétert'', mint az

r_{0}

és

β

paraméter függvényét! (Lásd: F-2. ábra.)

F-2. ábra

4.3. (1,0

+

0,2 pont) Határozd meg a végtelen távoli mozgás irányának

ϕ

szögét, mint a

β

paraméter függvényét! (Lásd: F-2. ábra.) Add meg a szög számszerű értékét a

β = \frac{3}{2} β_{esc}

esetre!
Segítség. A távolság négyzetének reciprokával csökkenő, centrális erőtérben mozgó testek ellipszis, parabola vagy hiperbola pályán mozognak. Az

m ≪ M

közelítés mellett a centrális gravitációs teret létrehozó

M

tömeg a pálya egyik fókuszában van. A koordináta-rendszer kezdőpontját ebben a pontban felvéve, a fenti pályák általános, polárkoordinátás egyenlete (lásd: F-3. ábra)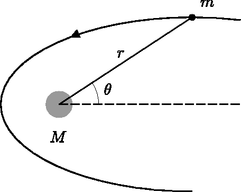

\begin{matrix} r (θ) = \frac{l}{1 - ε cos θ} \end{matrix}

alakú, ahol az

l

pozitív állandó a görbe paramétere (semi-latus-rectum = fél-merőleges-távolság),

ε

pedig a pálya excentriciása. A mozgást jellemző megmaradó mennyiségekkel kifejezve:

\begin{matrix} l = \frac{L^{2}}{G M m^{2}} és ε = {(1 + \frac{2 E L^{2}}{G^{2} M^{2} m^{3}})}^{1 / 2}, \end{matrix}

ahol

G

a gravitációs állandó,

L

a keringő test perdületének (impulzusmomentumának) nagysága a középpontra vonatkoztatva,

E

pedig a mechanikai energiája. (A potenciális energia zéruspontja a végtelenben van.)

F-3. ábra

A következő három esetet különböztethetjük meg:

i)

0 \leq ε < 1

, a görbe ellipszis (

ε = 0

esetén kör).

i i)

ε = 1

, a görbe parabola.

i i i)

ε > 1

, a görbe hiperbola.

2. feladat. Elektromos mennyiségek abszolút mérése

A XIX. században a technológiai és tudományos fejlődés szükségessé tette, hogy az elektromos mennyiségeknek általánosan elfogadott etalonja legyen. Úgy gondolták, hogy az új abszolút egységek csak a távolság, a tömeg és az idő etalonjaira épülhetnek, melyeket a francia forradalom után hoztak létre. 1861-től 1912-ig intenzív kísérleti munka folyt ezeknek az egységeknek a megalapozására. Itt három tanulmányt mutatunk be.

Az ohm meghatározása (Kelvin). Egy

N

menetes,

a

sugarú,

R

ellenállású kör alakú zárt tekercs állandó

ω

szögsebességgel forog a függőleges átmérője körül

{\vec{B}}_{0} = B_{0} \vec{i}

vízszintes mágneses térben.
1. (0,5

+

1,0 pont) Határozd meg a tekercsben indukálódó

ε

elektromotoros erőt, és a tekercs forgatásához szükséges

〈 P 〉

átlagos teljesítményt³! A tekercs önindukcióját hanyagold el!
A tekercs középpontjába egy kicsiny mágnestűt helyezünk az F-1. ábrán látható módon. A mágnestű lassan szabadon elfordulhat a

Z

tengely körüli vízszintes síkban, de a tekercs gyors forgását már nem tudja követni.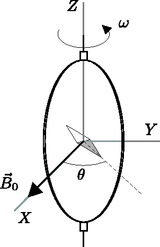

F-1. ábra

2. (2,0 pont) Az állandósult állapot elérése után a mágnestű kis

θ

szöget zár be a

{\vec{B}}_{0}

vektorral. Fejezd ki a tekercs

R

ellenállását ennek a szögnek és a rendszer többi paraméterének függvényében!
Lord Kelvin ezt a módszert használta az 1860-as években az ohm abszolút egységének rögzítéséhez. A forgó tekercs kiküszöbölésére Lorenz egy alternatív módszert javasolt, melyet Lord Rayleigh és Eleanor Sidgwick használt, és amit a következő részben megvizsgálunk.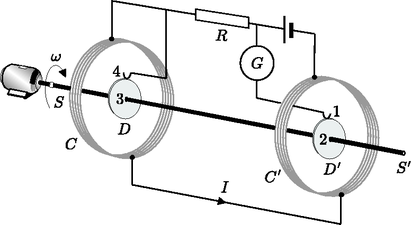

Az ohm meghatározása (Rayleigh, Sidgwick). A kísérleti elrendezés az F-2. ábrán látható. Az elrendezés két egyforma,

b

sugarú fémkorongból áll (

D

és

D'

), melyek a közös

S S'

fémtengelyre vannak erősítve. A tengelyt egy motor

ω

szögsebességgel forgatja. A szögsebességet

R

méréséhez változtatni lehet. A korongokat két egyforma,

a

sugarú,

N

menetes tekercs veszi körül (

C

és

C'

). A tekercsek úgy vannak sorbakötve, hogy az

I

áram a két tekercsen ellentétes irányban folyik keresztül. Az egész berendezés az

R

ellenállás mérésére szolgál.

F-2. ábra

3. (2,0 pont) Tegyük fel, hogy a

C

és

C'

tekercseken átfolyó

I

áram homogén mágneses teret hoz létre a D és D' korongok körül, melynek

B

nagysága megegyezik a tekercsek középpontjában kialakuló tér nagyságával. Számítsd ki⁴ a korongok peremén lévő 1-es és 4-es pont közt keletkező

ε

indukált elektromotoros erőt! Kihasználhatod, hogy a tekercsek közti távolság sokkal nagyobb a tekercsek sugaránál, és

a ≫ b

.
A korongokat az 1-es és a 4-es pontban érintkező kefék kapcsolják a hálózatba. A

G

galvanométer jelzi az 1‐2‐3‐4 áramkörben folyó áramot.
4. (0,5 pont) Az

R

ellenállást akkor mérjük, amikor

G

nullát mutat. Fejezd ki

R

értékét a rendszer fizikai paramétereivel!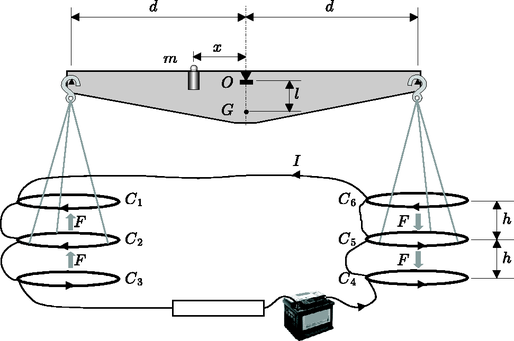

Az amper meghatározása. Ha két vezetőn áram folyik át, és megmérjük a köztük fellépő erőt, akkor ez az áram abszolút meghatározását teszi lehetővé. A Lord Kelvin által 1882-ben javasolt ,,árammérleg'' ezt az elvet használja. Az árammérleg hat egyforma,

a

sugarú, egymenetes, sorbakapcsolt tekercset tartalmaz (

C_{1} ... C_{6}

). A rögzített

C_{1}

C_{3}

C_{4}

és

C_{6}

tekercsek az F-3. ábrán látható módon két, egymástól

2 h

távolságra lévő vízszintes síkban fekszenek. A

C_{2}

és

C_{5}

tekercsek

d

hosszúságú mérlegkarokra vannak akasztva, és a mérleg egyensúlyi helyzetében egyforma messze vannak a két síktól.

F-3. ábra

I

áram úgy folyik át a tekercseken, hogy a

C_{2}

tekercsre felfelé, a

C_{5}

tekercsre lefelé mutató mágneses erő hat. Az

O

forgástengelytől

x

távolságra elhelyezett

m

tömeg szolgál arra, hogy a fent leírt egyensúlyi állapotot helyreállítsa abban az esetben, amikor a tekercseken áram folyik át.
5. (1,0 pont) Fejezd ki a

C_{2}

tekercsre ható, a

C_{1}

tekerccsel való mágneses kölcsönhatásból származó

F

erőt! Az egyszerűség kedvéért tételezd fel, hogy az egységnyi hosszra ható erő megegyezik a két végtelen hosszú párhuzamos vezető közt egységnyi hosszon fellépő erővel!
6. (1,0 pont) Az

I

áramot a mérleg egyensúlyi helyzetében mérjük. Fejezd ki

I

értékét a rendszer fizikai paramétereinek függvényében! A berendezés méretei olyanok, hogy a bal oldalon és a jobb oldalon lévő tekercsek közti kölcsönhatás elhanyagolható.
Legyen

M

a mérleg tömege (

m

és a ráakasztott részek nélkül), G a tömegközéppontja, az

\bar{O G}

távolság pedig

l

!
7. (2,0 pont) A mérleg egyensúlyi állapota stabilis, ha a

C_{2}

tekercs magassága kicsiny

δ z

, a

C_{5}

tekercsé pedig

- δ z

értékkel megváltozik. Határozd meg⁵ azt a

δ z_{{max}_{}^{}}

maximális értéket, ahol a mérleg az elengedés után még az egyensúlyi helyzet irányába kezd el mozogni!

3. feladat. Neutronok gravitációs mezőben

A megszokott klasszikus világban a földön rugalmasan pattogó labda a vég nélküli mozgás ideális példája. A labda csapdában van, nem mehet a földfelszín alá és a felső holtpont fölé. Kötött állapotban marad, mindig visszafordul és fölpattan. Csak a közegellenállás és az ütközés rugalmatlansága állíthatja meg, amitől viszont a következőkben eltekintünk.
Fizikusok egy csoportja a grenoble-i Laue‐Langevin Intézetben 2002-ben megjelentetett egy cikket⁶ a földi gravitációs mezőben végzett neutronejtési kísérletről. A kísérletben a jobbra mozgó neutronok szabadon estek egy vízszintes, neutrontükörként viselkedő kristályfelületre, ahonnan rugalmasan visszapattantak a kezdeti magasságukig, és ez ismétlődött

...

A kísérlet vázlatát az F-1. ábra mutatja. A rendszer egy

W

bemenőnyílásból, egy

M

neutrontükörből (

z = 0

magasságban), egy

L

hosszúságú

A

neutronelnyelő falból (

z = H

magasságban) és egy

D

neutrondetektorból áll. A neutronsugár állandó

v_{x}

vízszintes sebességgel repül az

A

és

M

közötti üregben

W

-től

D

-ig. Mindegyik neutron, amely eléri az

A

felületet, elnyelődik, azaz eltűnik a kísérletből. Azok, amelyek elérik az

M

felületet, rugalmasan visszaverődnek. A

D

detektor azon neutronok

N (H)

számát méri, amelyek egységnyi idő alatt elérik a detektort.

F-1. ábra

Az üregbe belépő neutronok sebességének

v_{z}

függőleges komponense mind pozitív, mind negatív irányban széles tartományban változik. Az üregbe belépő neutronok a tükör és az elnyelő felület között repülnek.
1. (1,5 pont) Határozd meg klasszikusan a

z

magasságban belépő neutronok

v_{z} (z)

függőleges sebességének azt a tartományát, amelyben a neutron eléri a detektort! Tedd fel, hogy

L

sokkal hosszabb, mint a feladatban bármely más hosszúság!
2. (1,5 pont) Számold ki klasszikusan az üreg

L_{c}

minimális hosszát, amely biztosítja, hogy az előző pontban szereplő sebességtartományon kívüli neutronok minden

z

esetén elnyelődjenek

A

-ban! Legyen

v_{x} = 10 ms^{- 1}

és

H = 50 μ m

.
Az

N (H)

átmenő neutronfluxust mérjük

D

-ben. Azt várjuk, hogy ez a mennyiség monoton növekszik

H

-val.
3. (2,5 pont) Határozd meg klasszikusan a detektort időegységenként elérő összes neutron

N_{c} (H)

számát, feltéve, hogy a belépő neutronnyalábban minden

v_{z}

sebesség és minden

z

magasság egyformán valószínű. A választ az üregbe egységnyi idő alatt, egységnyi

v_{z}

függőleges sebességtartományban és egységnyi

z

magasságtartományban belépő neutronok számát megadó

ϱ

állandóval fejezd ki!
A grenoble-i csoport által kapott eredmények nem egyeztek a fenti klasszikus jóslattal, helyette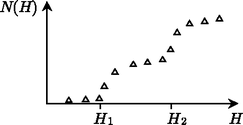

N (H)

kísérleti értékei hirtelen ugrásokat mutattak, amikor

H

bizonyos kritikus értékeket (

H_{1}, H_{2}, ...

) átlépett. Ezt mutatja vázlatosan az F-2. ábra. Más szavakkal, a kísérlet azt mutatta, hogy a neutron függőleges pattogó mozgása kvantált. Hasonlóan ahhoz, ahogy Bohr és Sommerfeld a hidrogénatom energiaszintjeit megkapta, itt is úgy fogalmazhatunk, hogy ,,az

S

hatás a

h

Planck-állandó egész számszorosa''. Ebben a feladatban

S

-et az

\begin{matrix} S = \int p_{z} (z) d z = n h, n = 1,2,3, ... \end{matrix}

összefüggés határozza meg (Bohr‐Sommerfeld kvantumfeltétel), ahol

p_{z}

az impulzus függőleges komponense, és az integrált a pattogás teljes periódusára kell elvégezni. Csak olyan neutronok haladhatnak az üregben, melyek a feltételt kielégítő

S

-sel rendelkeznek.

F-2. ábra

4. (2,5 pont) Számold ki azokat a

H_{n}

holtpontmagasságokat és

E_{n}

energiaszinteket (ahol

E_{n}

a függőleges mozgáshoz tartozó mechanikai energia), amelyeket a Bohr‐Sommerfeld kvantálás megenged! Add meg

H_{1}

számszerű értékét

μ

m-ben és

E_{1}

értékét eV-ban!
A kvantálással a hosszú üregen keresztülrepülő neutronok belépéskor egyenletes eloszlása megváltozik, és ezért detektáltak lépcsőszerű eloszlást (lásd az F-2. ábrát.) A továbbiakban az egyszerűség kedvéért egy

H < H_{2}

magasságú, hosszú üreget vizsgálunk. Klasszikusan minden, az 1. kérdésben meghatározott energiatartományban levő neutron keresztülmehet az üregen, de a kvantummechanika szerint csak azok, melyek energiája

E_{1}

. Az energiára és időre vonatkozó Heisenberg-féle határozatlansági reláció szerint ez az energiaérték meghatároz egy minimális repülési időt.
5. (2,0 pont) Becsüld meg a minimális

t_{q}

repülési időt és az üregnek ehhez tartozó minimális

L_{q}

hosszát, amely ahhoz szükséges, hogy meg tudjuk figyelni a neutronok

D

-ben mért számában az első éles növekedést. Legyen

v_{x} = 10 ms^{- 1}

.
Adatok:

\begin{matrix} Planck-állandó & h = 6, 63 \cdot 10^{- 34}Js, \\ fénysebesség vákuumban & c = 3, 00 \cdot 10^{8} ms^{- 1}, \\ elemi töltés & e = 1, 60 \cdot 10^{- 19}C, \\ neutron tömege & M = 1, 67 \cdot 10^{- 27}kg, \\ nehézségi gyorsulás & g = 9, 81 ms^{- 2}. \\ Ha szükséges, használd: & \int {(1 - x)}^{1 / 2} d x = - \frac{2 {(1 - x)}^{3 / 2}}{3}. \end{matrix}

¹A pályához tartozó keringési idő

T_{0}

²Nézd át a feladat végén található ,,segítséget''!

³Egy $X (t)$ periodikus mennyiség $〈 X 〉$ átlagértéke $〈 X 〉 = \frac{1}{T} \int_{0}^{T} X (t) d t$ , ahol $T$ a periódusidő.

⁴Szükséged lehet a következő integrálokra:

\begin{matrix} \int_{0}^{2 π} sin x d x = \int_{0}^{2 π} cos x d x = \int_{0}^{2 π} sin x cos x d x = 0, \int_{0}^{2 π} sin^{2} x d x = \int_{0}^{2 π} cos^{2} x d x = π, \end{matrix}

később

\begin{matrix} \int x^{n} d x = \frac{1}{n + 1} x^{n + 1} . \end{matrix}

⁵Feltételezd, hogy a tekercsek középpontjai közelítőleg egy vonalban maradnak!
Használd a következő közelítéseket: $\frac{1}{1 \pm β} \approx 1 \mp β + β^{2}$ vagy $\frac{1}{1 \pm β^{2}} \approx 1 \mp β^{2}$ , ha $β ≪ 1$ , és $sin θ \approx tg θ$ , ha $θ$ kicsi.

⁶V. V. Nesvizhevsky et al., ,,Quantum states of neutrons in the Earth's gravitational field.'' Nature, 415 (2002) 297., Phys Rev. D 67, 102002 (2003).